Semi-automatic Detection of Corticalis Borders in

Two-dimensional Radiographies to Improve

Pre-operative Planning

Marc Schlimbach and J¨urgen Wahrburg

Center for Sensor Systems (ZESS), Siegen University

Paul-Bonatz Street 9-11, 57076 Siegen, Germany

Abstract. This paper suggests an algorithm to detect corticalis borders in a ra-

diograph. It is robust against occurring interferences in radiographies, because it

is a global working procedure. This segmentation is part of semi-automatic as-

sistant functions, which are developed to support surgical interventions. The al-

gorithm will be introduced related to the calculation of the femoral CCD-Angle.

Further subjects of the presented proposal cover special aspects when using a

two-dimensional radiography for pre-operative planning instead of CT or MRT

scans.

1 Introduction

The work outlined in this paper is embedded in the development of the modiCAS as-

sistant system. modiCAS is the abbreviation for modular interactive computer assisted

surgery. It is a system to support the surgeon during surgical interventions. This pa-

per describes the determination of important surgical parameters which may later be

used during the intervention supported by navigation systems or a robot based assistant

system.

Radiography is the most used modality in orthopaedics and trauma surgery. The

challenge consists in extracting as many parameters as possible out of radiographies

during the planning phase to allow an optimal prearrangement of the intervention. An

additional problem is the scaling of radiographies. In contrast to the scaling of CT

or MRT scans, projection images of two-dimensional x-ray scanners do not contain

inherent scaling information.

Due to the intraoperative use of c-arms, radiographies are also generated during the

intervention. So it is possible to extract parameters to control a mechatronical assistant

system. For this task the scaling of radiographies is very important.

Thus there are several applications where the accurate and easy extraction of impor-

tant parameters for a surgical intervention is of high relevance. In order to support the

user here, we develop semi-automatic assistant functions within the modiCAS project.

A semi-automatic assistant function is a combination of automatic functions and

manual steps. All parameters which are computed automatically by an algorithm will

be transferred to a planning object. These planning objects allow the user interaction,

Schlimbach M. and Wahrburg J. (2009).

Semi-automatic Detection of Corticalis Borders in Two-dimensional Radiographies to Improve Pre-operative Planning.

In Proceedings of the 1st International Workshop on Medical Image Analysis and Description for Diagnosis Systems, pages 62-73

DOI: 10.5220/0001814500620073

 SciTePress

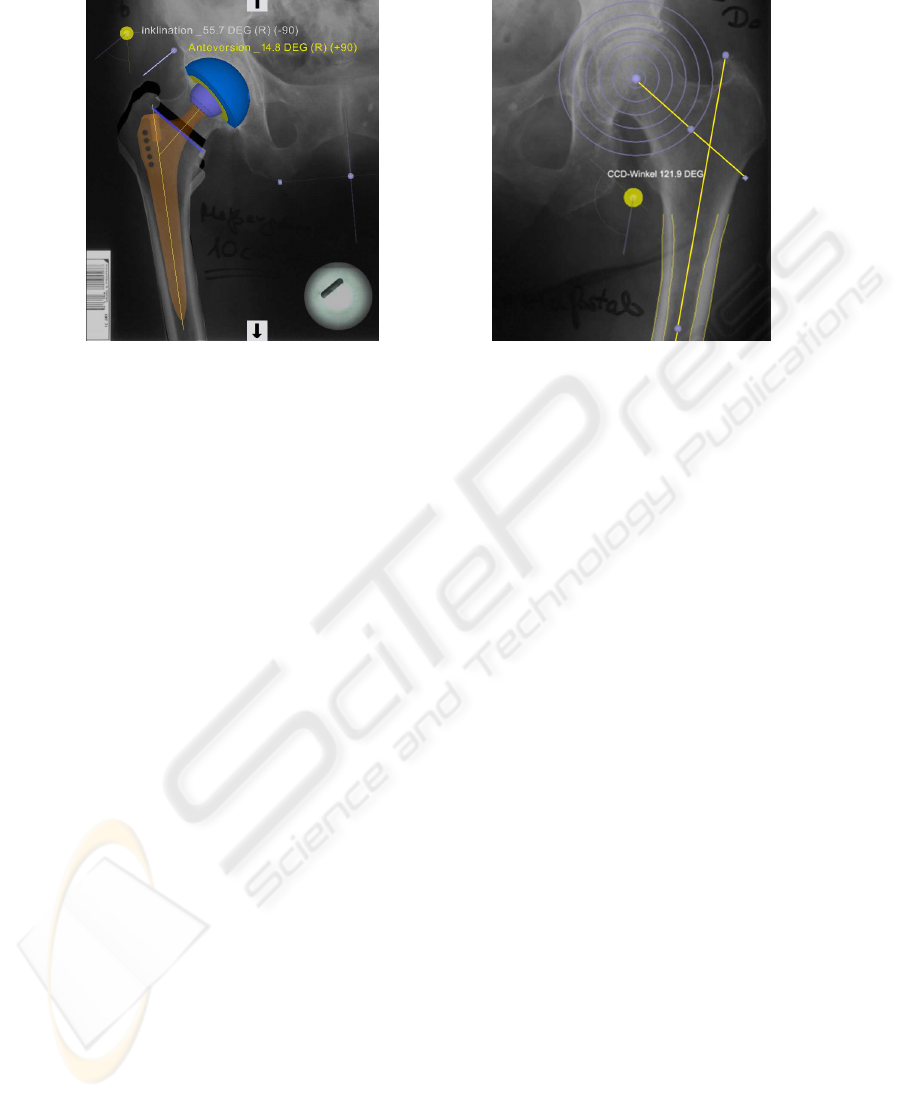
Fig.1. Screenshot of a hip replacement

planning with modiCAS-Planning.

Fig.2. Femur and neck axis to measure

the CCD-angle.

and the user has the chance to manipulate the parameter before he starts the next step

of the semi-automatic assistant function.

One advantage of such an assistant function compared to the manual creation of

planning objects is the advantage in time. Even in the case of planning standard inter-

ventions like hip replacements, time requirements play an essential part for the accept-

ability of such a planning tool.

This paper suggests a procedure to allow the fast and safe segmentation of long

bone corticalis borders in radiographies. This procedure is the base of a semi-automatic

assistant function to determine the CCD-angle of a femur bone. In a further step this as-

sistant function will make a proposal for the optimal femoral implant out of a database.

2 Problem

Hip replacement proceduresrequire the pre-operativeplanning of a pelvic and a femoral

component. For each component an appropriate size and type must be selected out of

a database. In the next step this component must be placed in the image data. Figure 1

shows a screen shot with a complete planning and three-dimensional implant models.

This planning is carried out using the software modiCAS-Planning.

The presented semi-automatic assistant function supports the surgeon during the plan-

ning of the femoral shaft component. Some patient speciﬁc parameters must be deter-

mined out of a radiograph to select a ﬁtting shaft implant.

Figure 2 shows the femoral axis and the neck axis which are two of these param-

eters. The angle between these axes is the CCD-angle. Apart from the size the CCD-

angle is an important criterion to select the shaft implant. Implant manufactures offer

shaft implants with different CCD-angles in adaptation to the varying anatomy of dif-

ferent patients.

It is possible to compute the femoral axis out of the corticalis borders with a smooth-

ing function. The shown rotation center of the head is one point of the neck axis. In

addition to the CCD-angle the corticalis borders and the rotation center of the head are

other criteria which are important during the implant selection.

The proposedprocedureto determine the corticalis borders should be released within

the existing surgical tool modiCAS-Planning. The functionality will be explained at the

femoral bone. The aim is to support the user during the implant selection and position-

ing of a shaft.

3 Speciﬁc Aspects using Radiographies

If radiographies are used for planning, it will be important to take some speciﬁc aspects

in consideration.In this paper two aspects are discussed. The ﬁrst aspect is the scaling of

radiographies. The second aspect is the reconstruction of three-dimensional information

out of a series of two-dimensional radiographies.

3.1 Scaling of Radiographies

As known radiography is a projection bases technology. Depending on the arrangement

(Figure 3) of x-ray source, x-ray detector and patient the recorded image appears greater

by a certain image scaling factor (1). For measurement of length in radiographies the

scaling factor must be known, but it is a problem to determine the correct one.

Source-Detector

Plane-Detector

X-raysource

X-raydetector

Table

scalingplane

Fig.3. Assembly of an X-ray equipment for radiography.

The scaling factor (1) describes the size difference between a pixel on the detector

and the imagined region in the patient.

scale

SourceT oDetector

SourceT oP lane

(1)

In this equation S

SourceT oDetector

is the distance between the focus of the x-ray source

and the x-ray detector. The value of S

SourceT oP lane

is the distance between the focus

and a plane through the patient which is parallel to the x-ray detector. The height of this

scaling plane above the detector depends on the one hand on the use case and on the

other hand on the individual anatomy of the patient. These two dependences will be not

reﬂected, if a standard scaling factor is used. The dependency between scaling factor

and scaling plane is shown in Figure 4.

5 7 9 11 13 15 17 19 21 23 25 27 29

1.1

1.2

1.3

1.4

1.5

Height [cm]

1 / scaling factor

Fig.4. Scaling factor depending on the

height of the scaling plane. The distance

between focus and detector is 100 cm.

5 7 9 11 13 15 17 19 21 23 25 27 29

−20

−15

−10

−5

Height [cm]

Scaling error [%]

Fig.5. Percental scaling error by using a

standard scaling factor of 1:1.2 depend-

ing on the height of the scaling plane.

In equation (2) the scaling factor depends on the distance h between the x-ray detector

and the scaling plane through the patient.

scale

SourceT oDetector

− h

(2)

Figure 5 shows the percentage error which will occur, if a standard scaling factor of

1:1.2 is used instead of the correct scaling factor. The graph illustrates the scaling error

of round about one percent for every centimetre change in altitude.

There are the following consequences relating to the selection of a cup implant.

Usually cup implants are available in size steps of 2 mm. The percentage difference

between a cup with a diameter of 56 mm and one with 58 mm is round about 3.5% for

example. So it is possible to plan a cup that differs in one or two size steps to the cup

which is needed.

It is clear that the standard scaling factor, which is often used in DICOM ﬁles,

allows no exact measurements. Another area where such standard scaling factors are

applied, are two-dimensional implant templates. These templates are used to make a

manual planning on not scaled radiographies by using a light box.

One possible solution to reduce this problem is a scaling body with a known size. This

scaling body must be placed in the radiography on the height of the required scaling

plane. At the beginning of a new planning the size of this scaling body can be measured

in the image to get the scaling factor. The accuracy of a scaling factor which is deter-

mined in that way depends on the error which is made by placing the calibration body

on the required height. If only angles like the CCD-Angle should to be measured in a

radiograph, a scaling will be not necessary.

3.2 2D-3D Reconstruction

If there is a set of radiographies available during the planning time, it will be possi-

ble to extract some three-dimensional information out of these images. Therefore it is

required, that the recording situation of each image is known.

There are some algorithms for this kind of three-dimensional reconstruction sug-

gested in the literature. The procedure described in [1] is qualiﬁed for pre-operative

planning. It bases on a special calibration body which must be placed in the image dur-

ing the recording time. So it is possible to reconstruct the recording situation during the

planning and pose the images in the virtual planning space.

A navigated c-arm is another possibility to get radiographies with a known record-

ing situation. With this technology the recording situation is delivered directly by the

c-arm and no complex algorithms are used by the reconstruction.

Semi-automatic assistant functions would be appropriateto generate three-dimensional

information out of such arranged radiographies during the intervention in a short time.

4 Known Procedures for Corticalis Detection

Several procedures have been developed in the last years to detect the femoral contour,

but most of these proposals were limited to the outer femoral contour. Some of the

proceduresare based on a two-dimensionalfemur model, which is registered atlas based

in the ﬁrst step. In the second step a ﬁtting procedure deforms the two-dimensional

model to the real contours in the x-ray. The active contour algorithm is one option to ﬁt

the model. [4], [6].

Another possibility is the deformation of a three-dimensional statistical model as

described in [5]. This approach needs more than one radiograph. In addition the orien-

tation between the radiographies is required. This work makes a proposal of a procedure

that detects the inner and outer contour of a corticalis in a fast and stable way.

5 New Procedure to Detect Corticalis Borders

Radiographies often have interferences like shades, channels or local overlapping. Due

to this it is complicate to get good and save results with procedures which have a lo-

cal operation method like the path ﬁnding algorithm. Another problem which must be

solved to use a path ﬁnding algorithm is the detection of the starting points. The new

proposal of this paper has a global operation method. Due to this it has the advantage

to be more robust against local interferences.

The procedure of this proposal is divided in several steps. Within these steps some

standard methods out of the image processing are used. The general functionality is as

follows. At ﬁrst as many as possible groups composed of 4 points were build. Each of

these points should be a part of the corticalis borders. The following steps process some

plausibility tests to ﬁlter out point groups that don’t completely belong to the corticalis

borders.

5.1 Compute Gradients

The ﬁrst step computes the gradient in x-direction. This is done by a Sobel operator (3)

from [2]. The advantage of this operator is its small angle error. Further the gradient

image will be normalized.

′





3 0 − 3

10 0 −10

3 0 − 3





(3)

5.2 Quadruple Building

In this step the gradient image of the previous step will be processed line by line. If

the application requires only some interpolation points of the corticalis borders, it will

be possible to process only each n-th line of the image. The size of n depends on the

required distance between the interpolation points.

The criteria which are used to decide weather an image point belongs to the searched

contour or not are derived from the following considerations.

The gradient through a bone in x-direction has a typical history shown in Figure

6. The recognizable minima and maxima of the inner and outer corticalis borders are

named with x

· · · x

. Such a group of four points will be named as a quadruple in

the following text. In a quadruple x

and x

represents minima, x

and x

represents

maxima. A further condition for a quadruple is that the Points x

· · · x

are in rising

x-direction. There are some advantages caused by the combination of four points to a

quadruple:

– It is possible to deﬁne requirements, which must be fulﬁlled by each quadruple.

– It is possible to compute the center point of each quadruple. The center points of

one femur must be up to a line approximately.

– In the end it will be sure that there is the same number of points on both femoral

sides. Due to this it will be simpliﬁed to compute the center axis of the bone with a

linear smoothing function.

The algorithm creates two lists, to identify all possible quadruples of the current

image row. The ﬁrst list stores all positions of the row where the gradient reaches a local

maximum. The second list stores all positions of local minima. Thereto the algorithm

runs through the current image row and detects minima and maxima in an alternating

way. A new extrema will be found, if the magnitude decreases in the following at least

80% or brakes through the zero line.

After detecting all extreme positions of the current image row only the extreme

positions with the biggest magnitude of the gradient will be used furthermore, to sup-

press noise and other interferences. A pelvic overview with two femora contains 4 max-

ima and 4 minima which are interesting. By disturbance or other objects like radiation

protectors there could be other vertical edges which produce extreme positions in the

horizontal gradient. These extrema could have a higher magnitude than the searched ex-

treme positions. Based on the experience of our tests a maximum number of 15 minima

and 15 maxima are adequate to be sure that the searched extreme positions are included.

After this the algorithm builds all possible quadruples out of the maximal 30 local

axtrema. Each of these combinations will be tested with several criteria. If a quadruple

passes all tests, it will be saved as a candidate of the current image row for further

processing steps.

0 10 20 30 40 50 60 70 80 90

−40

−20

100

120

140

160

x−position

gradient and gray value

gray value

gradient

X1 X4X3X2

Fig.6. Gray value and gradient in x-direction through a femur with the extreme positions

· · · x

These tests analyze several characteristics of the gradient at the positions x

· · · x

and can be divided in two groups. The ﬁrst group is responsible for the magnitude of

the gradient in the extreme positions. The second group checks the geometrical charac-

teristics.

The following rules represent the conditions of the gradients magnitude.

|2 · grad(x

)| > |grad(x

)| (4)

|2 · grad(x

)| > |grad(x

)| (5)

||grad(x

)| − |grad(x

)|| <

(6)

||grad(x

)| − |grad(x

)|| <

(7)

The inequality (4) is based on the observation that the minimum at position x

is usually

bigger than the maximum at position x

. The rule (5) follows analogous to that for the

positions x

and x

. The rules (6) and (7) are the results of the fact that the magnitude

of the extremums at x

and x

respectively x

and x

are round about the same size.

The following substitutions are introduced for better expression of the geometrical

rules.

= x

− x

(8)

= x

− x

(9)

= x

− x

(10)

= x

− x

(11)

and w

are the latitudes of the left respectively right corticalis. The outer and

inner diameter of the bone is described with d

and d

The latitudes of the left and right corticalis usually do not vary more than a factor

of two. This is the reason of inequality (12). The proportions between the left and right

corticalis on the on hand and the inner and outer diameter on the other hand are for-

mulated with the rules (13, 14, 15, 16). The acceptable ratio between inner and outer

diameter is formulated with rule (17). The factors which are used in these rules are se-

lected in a way that no quadruple of the test data will fail a test, if it is completely up to

the femoral corticalis borders.

< w

< 2 · w

(12)

0.5 · w

< d

< 5 · w

(13)

0.5 · w

< d

< 5 · w

(14)

8 · w

> d

(15)

8 · w

> d

(16)

4.2 · d

> d

> 1.2 · d

(17)

5.3 Localise the Femora

In this step the algorithm detects the number of bones and the detected quadruples will

be attached to the different bones. In the case of femur detection there can be an image

with one or two femora.

Therefore the x-axis will be divided into three parts of equal length, and the centre

point as the arithmetic average of the four points will be computed for each quadruple.

On basis of the centre point position the algorithm allocates each quadruple to one

of the three segments. When all quadruples are attached to a segment the number of

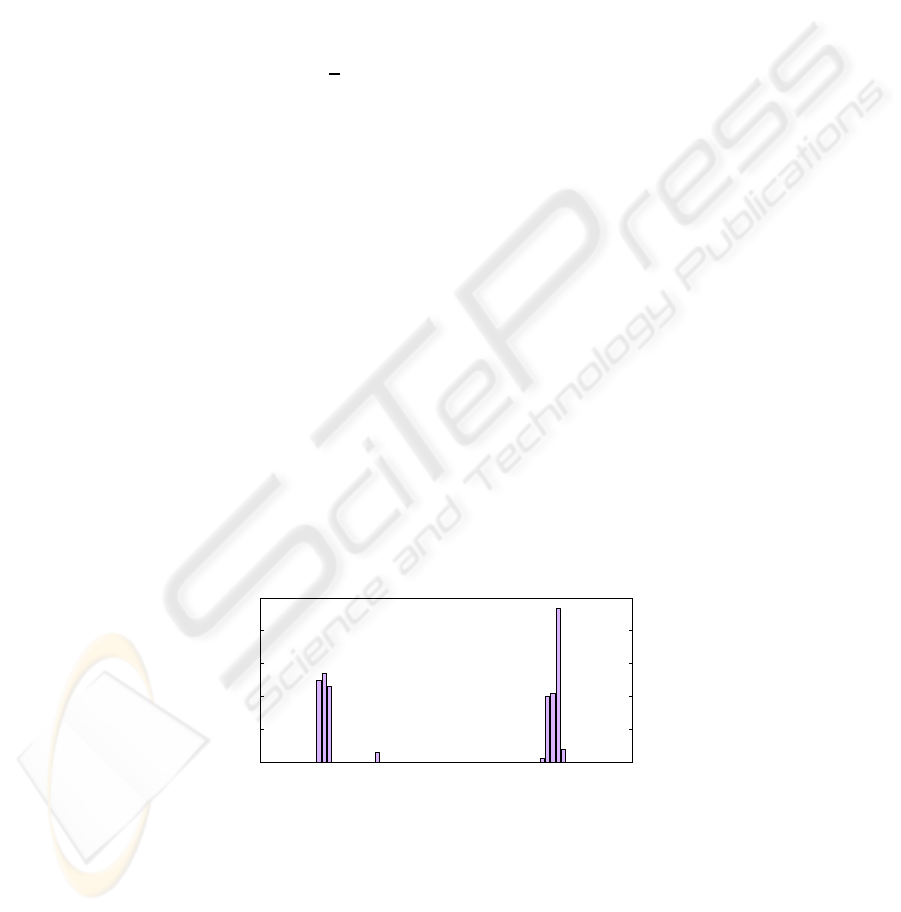
quadruples per segment can be compared (Figure 7).

x−position

number of quadruples

Fig.7. Distribution of the centre points over the x-axis in the case of a pelvic overview.

If the left and the right segment have more quadruples than the inner segment, the

image is a pelvic overview with two femora. In this case the quadruples which are

attached to the inner segment will be deleted and the quadruple attached to the outer

segments will be attached to two femoral objects. In the other case only one femur is

visible in the image and the algorithm use the quadruples of the inner segment to build

one femoral object

5.4 Filtering with the Hough Transformation

This step will be passing through for each detected femur. It computes a ﬁrst estimation

of the center axis of the quadruples which are attached to a femur.

At this time the algorithm assumes that most of the points which are attached to a

femur are up to the corticalis contour. Due to this there will be a clearly straight, if the

center points of each quadruple that is attached to a femur will be painted in an image.

Although there may be some quadruples with center points more or less far away from

this axis. This points can be called as noise.

For estimation of the center axis a procedure is needed that is robust against these

outliers. The Hough transformation for line detection is one candidate. The result of

the Hough transformation is only inﬂuenced by the points which are part of the line.

All other points have no inﬂuence to the result as long as there is no accumulator ﬁled

with more points than the accumulator ﬁeld of the searched straight. Alternatively we

have made some trails with a smoothing function. But at this processing time there can

be too much center points far away from the bone axis. These points would have a big

inﬂuence to the results of such a smoothing function particularly combined with short

bone segments. In this case there will be only a low number of image rows and the

inﬂuence of such outlier increases.

However, the Hough transformation has a further big advantage, because it is very

simple to shrink the allowed range of angles. If images with perpendicular aligned bones

like femora are processed, the asked straight will be as well more or less perpendicular

aligned.

The distance between the center point and the estimated bone axis is the criterion

for ﬁltering in this step. To deﬁne a limit for this distance the standard derivation of the

distance of all center points will be computed. Afterwards all quadruples with a greater

distance between their center point and the estimated axis than the calculated standard

derivation will be ﬁltered out.

5.5 Final Filtering

The last step is the ﬁltering procedure with a smoothing function. Thereto the algorithm

computes a best-ﬁt line with a smoothing function based on the method of smallest

square deviation.

If there are more than one quadruple per image row and femur, the quadruple with

the closest center point will be selected. All other quadruples will be ﬁltered out and a

recalculation of the best-ﬁt line starts.

The ﬁnal best-ﬁt line is the center axis of the bone.

6 Realization within the Modicas Software Framework

The suggested procedure was realized as plug-in of the surgical planning software

modiCAS-Planning which is a part of the modiCAS-Project. This project realizes the

complete chain of a surgical intervention.

Therefore it is possible to create a planning based on two- or three-dimensional

modalities. Afterwards the surgeon can be supported during the intervention by a mecha-

tronical assistant system.

The planning software is designed as a framework. Further it has a plug-in interface

to allow simple appending of new functions to the system. Additional the software has

an own scripting language to bind the operations of a planning or an intervention in

a workﬂow. The advantage of this workﬂow concept is the easy and fast method of

interaction. The user will be guided step by step and there is no need to select the next

function manually. To support the new functions of the plug-ins in a workﬂow, it is

although possible to extend the scripting language via plug-ins.

The plug-in which was developedto demonstrate the procedure is able to create line

planning-objects for the femoral axis and contour planning-objects for the corticalis

borders, which can be used for further planning steps.

A second plug-in was realized for semi-automatic scaling of radiographies. This

plug-in detects a round calibration body with the procedure suggested in [3]. The sug-

gested algorithm bases on the detection of vectors with opposite directions. If a calibra-

tion body is found, the plug-in creates a circle planning object which will be modiﬁed

by the user, if there is any need. After conﬁrmation by the user the image will be scaled

to the correct size.

7 Discussion

The procedure was validated with twenty radiographies from ﬁve different X-ray equip-

ments for radiography. These images contain 29 femora which should be detected. The

results have been compared to manual created femoral axis.

It is enough to get some base points of the corticalis borders to compute the femur

axis. The pixel distance between these points depends on the image resolution and the

expected size of the bone. During this validation, the algorithm worked on each 10th

image row. The reason for this is the decreasing computing time which is important in

a semi-automatic assistant function to produce no time of waiting for the user.

It was possible to detect whether the image was a pelvic overview with two femora

or a single sided radiography. There was only one image with a detected quadruple

which doesn’t belong to a femur. Figure 8 shows the result of one of the images.

In the upper part of the femur, where the corticalis becomes smaller, not all quadruples

were found, but this makes no big difference concerning the calculation of the femoral

axis.

The detection of the outer corticalis contour was robust. On the inner side there are

5 of 29 femora with inaccuracies in one or two of the detected quadruples. In all of

these cases an inner contour point is moved too much in the direction of the femoral

center axis (Figure 9). Due to the low number of faulty points this has no consequence

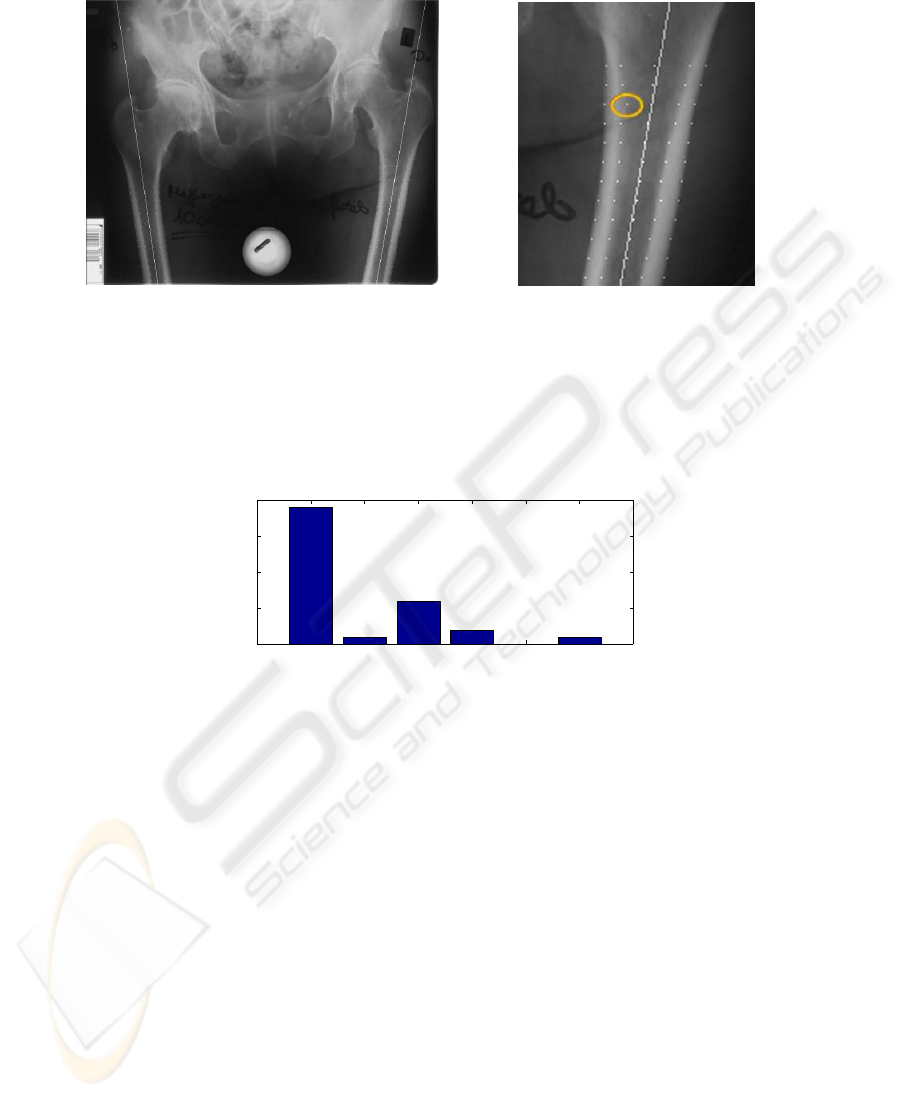
Fig.8. Detected quadruples and femur

axis within the original radiography.

Fig.9. Faulty pixel of the inner femoral

corticalis border.

to the detection of the femoral axis. It should be able to resolve this problem by a post

processing of the contour points.

0 1 2 3 4 5

error in degree

quantity

Fig.10. Results of the validation. 28 of 29 femora were detected in 20 radiographies.

Figure 10 shows the differences between the detected femoral axes compared to the

manual created axes. In 19 of 28 cases there were no error. One femur could not be

found.

Also radiographies of patients who already had one or two implants were tested. In

these images it was possible to detect the corticalis only below the implant.

The presented algorithm needs a vertical aligned long bone. In the tested images the

femora were rotated 13

◦

at maximum. In this rage of rotation no degeneration of the

results could be observed. If it is known that the long bone is horizontal aligned, it will

be possible to rotate the image or to use image cols instead of image rows during the

computation.

Due to these results the suggested procedure to detect long bone corticalis borders

is stable and accurate enough to use it in combination with the semi-automatic assistant

function described in this paper. Similarly the computing time round about 4 seconds

on a standard computer is short enough.

Table 1. Differences between manual and automatic detected femoral axes.

Results

minimal derivation 0

◦

maximal derivation 5

◦

standard derivation 1,53

◦

not founded femora 1

In the next time we will validate the procedure with an expanded amount of images.

Additionally we plan to test the algorithm with other types of bones.

8 Conclusions

This contribution explained a procedure to detect the corticalis borders of a long bone.

The procedure was classiﬁed by describing the use cases and alternative procedures.

The stable and accurate detection of the femoral axis and the femoral corticalis

borders and their use in a semi-automatic assistant function was the reason to develop

the presented procedure.

The suggested procedure was realized as a plug-in for the surgical planning tool

modiCAS-Planning. First steps of the validation were auspicious.

References

1. Groß, I.: Entwicklung eines Softwaresystems zur universellen Planung chirurgischer Ein-

griffe an 2D- und 3D- Bildmodalit¨aten. Shaker-Verlag, Aachen (2004)

2. J¨ahne, B.: Digital Image Processing: Concepts, Alogorithms and Scientiﬁc Applications. 6th

revised and extended edition. Springer-Verlag, Berlin Heidelberg New York (2002)

3. Rad A. A., Faez K., Qaragozlou N.: Fast Circle Detection Using Gradient Pair Vectors. Lec-

ture Notes in Computer Science. Springer-Verlag, Berlin Heidelberg New York (2003) 879-

887

4. Chen Y., Ee X., Leow W. K., Howe T. S.: Automatic Extraction of Femur Contours from

Hip X-Ray Images. Lecture Notes in Computer Science. Springer-Verlag, Berlin Heidelberg

New York (2005) 200-209

5. Dong X., Zheng G., Ballester M.A.G.: Automatic Extraction Of Femur Contours From Cal-

ibrated X-Ray Images: A Bayesian Inference Approach. Applications of Computer Vision,

IEEE Workshop. I. C. Society, Hrsg. (2007)

6. Kiattisin S., Chamnonghtai K.: Noninvasive Femur Bone Volume Estimation Based on X-

Ray Attenuation of a Single Radiographic Image and Medical Knowledge. IEICE Transac-

tions on Information and Systems. (2008) 1176-1184