
A 2D TEXTURE IMAGE RETRIEVAL TECHNIQUE BASED ON
TEXTURE ENERGY FILTERS
Motofumi T. Suzuki, Yoshitomo Yaginuma and Haruo Kodama
National Institute of Multimedia Education, 2-12 Wakaba, Mihama-ku, Chiba-shi 261-0014, Japan
Keywords:
Laws’ filters, Convolution, 2D Image Database, Image Retrieval, Shape Features.
Abstract:
In this paper, a database of texture images is analyzed by the Laws’ texture energy measure technique. The
Laws’ technique has been used in a number of fields, such as computer vision and pattern recognition. Al-
though most applications use Laws’ convolution filters with sizes of 3 × 3 and 5 × 5 for extracting image
features, our experimental system uses extended resolutions of filters with sizes of 7× 7 and 9 × 9. The use
of multiple resolutions of filters makes it possible to extract various image features from 2D texture images
of a database. In our study, the extracted image features were selected based on statistical analysis, and the
analysis results were used for determining which resolutions of features were dominant to classify texture
images. A texture energy computation technique was implemented for an experimental texture image retrieval
system. Our preliminary experiments showed that the system can classify certain texture images based on
texture features, and also it can retrieve texture images reflecting texture pattern similarities.
1 INTRODUCTION
In the 1990s, intensive research was conducted
on content-based image retrieval methods. Unlike
traditional keyword-based image retrieval methods,
content-based image retrieval methods have used im-
age features as indices for image databases. The im-
age features describe characteristics of the images
which include colors, shapes and textures. Since im-
age feature indices can be extracted automatically by
using software programs, this process is more ef-
ficient and faster compared to that of keyword in-
dices which are assigned by human hands. Various
image feature extraction techniques have been pro-
posed based on computer algorithms, such as co-
occurrence matrices (Haralick et al., 1973), Markov
random field modeling (Cross and Jain, 1983), Gabor
filtering (Manjunath and Ma, 1996), Wavelet (Chang
and Kuo, 1993), and HLAC (Kato, 1992). Also, vari-
ous statistical learning techniques have been proposed
to improve retrieval rates by learning from the sam-
ple image data (Kato, 1992). Such techniques include
use of self-organizing maps (SOM), neural networks
(NN) and support vector machines (SVM). Details of
image features and a related retrieval technique sur-
vey can be found in several papers (Veltkamp and
Tanase, 2000) (Datta et al., 2008).
In our experiments, the famous Laws’ texture en-
ergy measure technique is applied to a 2D texture
image database. Although a typical application uses
Laws’ filters of 3× 3 and 5× 5, the sizes of the filters
were extended to 7× 7 and 9 × 9 in our experiments.
These multiple resolutions of the filters were used for
extracting image features from images of a texture
database. The extracted features were analyzed by
linear discriminant analysis to determine which res-
olutions of features were best suited for classifying
the texture database. Also, principal component anal-
ysis (PCA), and the k-nearest neighbor (KNN) algo-
rithm was used for the similarity retrieval of a texture
database.
2 TEXTURE ENERGY FILTERS
In this section, (1) Laws’ texture energy measures, (2)
convolution and (3) rotation invariant features are dis-
cussed.
2.1 Laws’ Texture Energy Measures
The texture analysis technique based on the texture
energy measure which was developed by K. I. Laws
145
T. Suzuki M., Yaginuma Y. and Kodama H. (2009).
A 2D TEXTURE IMAGE RETRIEVAL TECHNIQUE BASED ON TEXTURE ENERGY FILTERS.
In Proceedings of the First International Conference on Computer Imaging Theory and Applications, pages 145-151
DOI: 10.5220/0001820701450151
Copyright
c
SciTePress

(Laws, 1979) (Laws, 1980) has been used for many
applications of image analysis for classification and
segmentation. The texture energy measurements for
2D images are computed by applying convolution fil-
ters. In the technique, three basic filters were used as
follows:
L3 = (1 2 1)
E3 = (-1 0 1)
S3 = (-1 2 -1)
The initial letters of these filters indicate Local av-
erage (or Level), Edge detection, and Spot detection.
The numbers followed by the initial letters indicate
lengths of the filters. In this case, the length of the
filters is three. Often, extended lengths of filters are
used for 2D image analysis. The extension of the fil-
ters can be done by convolving the pairs of these fil-
ters together. For example, filters with a length of five
can be obtained by convolving pairs of filters with a
length of three. In this convolution process, nine fil-
ters (3 × 3) can be formed, and five of them are dis-
tinct. The following is a set of one dimensional con-
volution filters of a length of five:
L5 = (1 4 6 4 1)
E5 = (-1 -2 0 2 1)
S5 = (-1 0 2 0 -1)
W5 = (-1 2 0 -2 1)
R5 = (1 -4 6 -4 1)
The initial letters of these filters stand for Local
average (or Level), Edge, Spot, Wave, and Ripple.
All filters are zero-sum filters except for the L5 fil-
ter. Many applications use Laws’ filter with a size of
3 and 5 for extracting texture energyvalues. In our ex-
periments, we have extended the filter sizes to 7 and
9. The filters of 7 can be obtained by convolving fil-
ters of a length of five and filters of a length of three
as follows:
Xa7 = ( 1, 6, 15, 20, 15, 6, 1 )
Xb7 = ( 1, 4, 5, 0, -5, -4, -1 )
Xc7 = ( -1, -2, 1, 4, 1, -2, -1 )
Xd7 = ( 1, 0, -3, 0, 3, 0, -1 )
Xe7 = ( 1, -2, -1, 4, -1, -2, 1 )
Xf7 = ( 1, -4, 5, 0, -5, 4, -1 )
Xg7 = ( -1, 6, -15, 20, -15, 6, -1 )
By using a similar approach, one dimensional ker-
nels of a length of nine are obtained as follows:
All the kernels are zero-sum kernels except for
Xa7 and Ya9. Simple sequential labels X and Y were
assigned for the filters 7 and 9 for convenience, al-
though more meaningful labels such as L, E, S, W
Ya9 = ( 1, 8, 28, 56, 70, 56, 28, 8, 1 )
Yb9 = ( 1, 6, 14, 14, 0, -14, -14, -6, -1 )
Yc9 = ( -1, -4, -4, 4, 10, 4, -4, -4, -1 )
Yd9 = ( 1, 0, -4, 0, 6, 0, -4, 0, 1 )
Ye9 = ( 1, 2, -2, -6, 0, 6, 2, -2, -1 )
Yf9 = ( -1, 2, 2, -6, 0, 6, -2, -2, 1 )
Yg9 = ( -1, 4, -4, -4, 10, -4, -4, 4, -1 )
Yh9 = ( 1, -8, 28, -56, 70, -56, 28, -8, 1 )
Yi9 = ( 1, -6, 14, -14, 0, 14, -14, 6, -1 )
and R can be used. (Obviously, Xa7 can be labeled
L7, and Ya9 can be labeled L9.)
These one dimensional filters are used to gener-
ate two dimensional filters by combining these one
dimensional filters. The set of two dimensional filters
with lengths of three (3× 3) are as follows:
L3L3, L3E3, L3S3
E3L3, E3E3, E3S3
S3L3, S3E3, S3S3
In a similar manner, two dimensional filters with
the lengths of 5 × 5, 7 × 7 and 9 × 9 can be ob-
tained. Furthermore, three dimensional filters such as
3 × 3 × 3 can be generated by combining basic one
dimensional filters (Suzuki and Yaginuma, 2007).
2.2 Convolution
Once the two dimensional filters are obtained, these
filters are used to convolve the 2D texture image. The
convolution of image I and filter F with a size of 2t +
1 by 2t + 1 is expressed by the following equation:
R(i, j) = F(i, j)∗I(i, j) =
t
∑
k=−t
t
∑
l=−t
F(k,l)I(i+k, j+l)
(1)
where ’∗’ denotes two dimensional convolution com-
putation. For the next step, the windowing process
is applied to convolved images. In this process, tex-
ture energy values are computed. Every pixel in the
convolved images is replaced with a texture energy
measure value at the pixel. In the Laws’ paper, a
15 × 15 square around each pixel is added together
with the values of the neighborhood pixels. In this
computation, Laws introduced ”squared magnitudes”
and ”absolute magnitudes” to compute texture energy
(Laws, 1979) (Laws, 1980). For considering compu-
tation efficiency, ”absolute magnitude” is used in gen-
eral. This computation process can be expressed by
the following equation:
E(l,m) =
l+t
∑
i=l−t
m+t
∑
j=m−t
|K(i, j)| (2)
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
146
where K is the local features, and it is smoothed at
position (l,m) by using a (2t + 1) × (2t+ 1) window.
2.3 Rotation Invariant Features
Some filters are identical if they are rotated 90 de-
grees. The features which are computed from the fil-
ters can be combined as similar features, and these
features are treated as rotation invariant features in
the order of 90 degrees. For example, feature E5L5
can be combined with L5E5, and newly created fea-
tures are denoted as E5L5
R
where R means the ”ro-
tation invariant” feature. On the other hand, some
features such as E5E5, S5S5, W5W5 and R5R5 can
not be combined. Since the rotation invariant fea-
tures were combined with two features, the feature
values were scaled by 2. Therefore, the rotation in-
variant features are divided by 2 for the purpose of
normalization. Figure 1 shows rotation invariant fea-
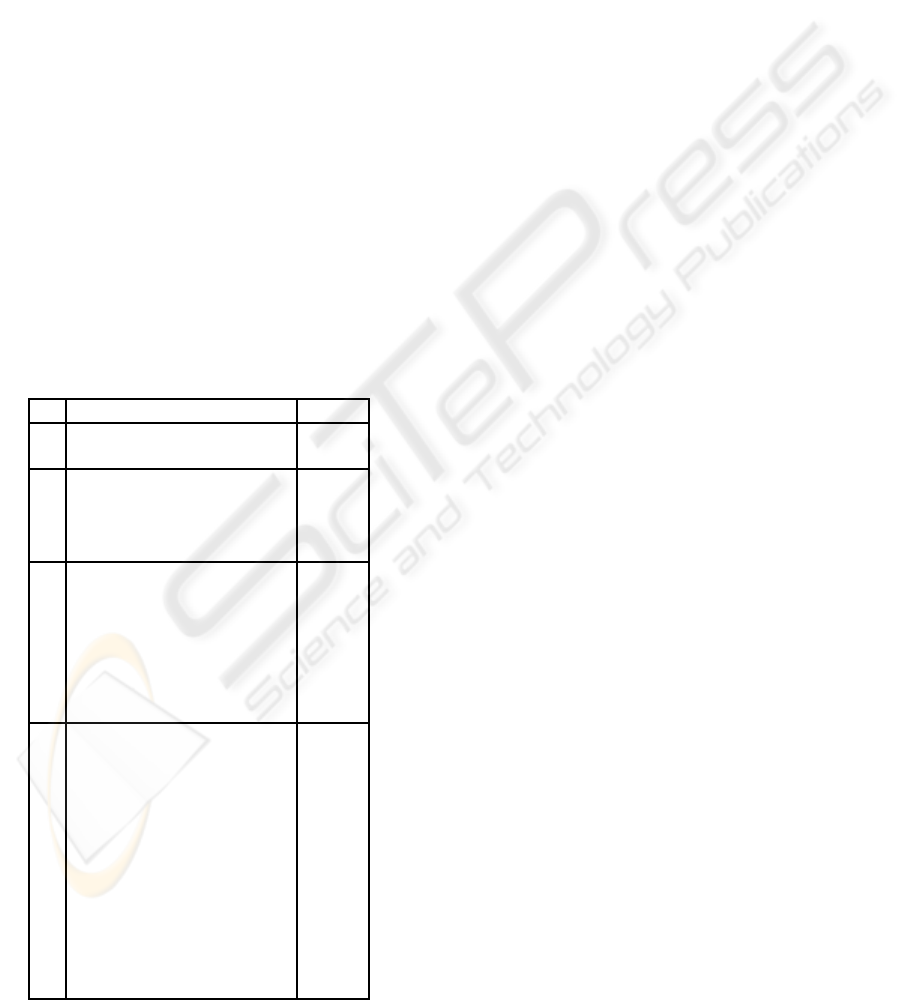
tures for filter lengths of 3× 3, 5× 5, 7× 7 and 9× 9.
(In this paper, rotation invariant features are denoted
as 3 × 3
R
, 5 × 5
R
, 7 × 7
R
and 9 × 9
R
, respectively.)
Also the number of corresponding rotation invariant
features is shown in Figure 1. The number of rota-
tion invariant features F
r
can be computed by equa-
tion F
r
= n
2
− ((n
2
− n)/2) where n is filter size.
R. Rotation Invariant Features Num.
3
2
L3L3,L3E3
R
,L3S3
R
,E3E3 9 → 6
E3S3
R
,S3S3
5
2
L5L5,L5E5
R
,L5S5
R
,L5R5
R
25 → 18
L5W5
R
,E5E5,E5S5
R
,E5R5
R
E5W5
R
,S5S5,S5R5
R
,S5W5
R
R5R5,R5W5
R
,W5W5
7
2
XaXa7,XaXb7
R
,XaXc7
R
,XaXd7
R
49 → 28
XaXe7
R
,XaX f7
R
,XaXg7
R
,XbXb7,
XbXc7
R
,XbXd7
R
,XbXe7
R
,XbX f7
R
XbXg7
R
,XcXc7, XcXd7
R
,XcXe7
R
XcX f7
R
,XcXg7
R
,XdXd7,XdXe7
R
XdX f7
R
,XdXg7
R
,XeXe7, XeX f 7
R
XeXg7
R
,X f X f7,X fXg7
R
,XgXg7
9
2
YaYa9,YaY b9
R
,YaY c9
R
,YaYd9
R
81 → 45
YaYe9
R
,YaY f9
R
,YaY g9
R
,YaY h9
R
YaYi9
R
,YbYb9,YbYc9
R
,YbYd9
R
YbYe9
R
,YbY f9
R
,YbYg9
R
,YbYh9
R
YbYi9
R
,YcYc9,YcYd9
R
,YcYe9
R
YcY f 9
R
,YcYg9
R
,YcYh9
R
,YcYi9
R
YdYd9,YdYe9
R
,YdY f9
R
,YdYg9
R
YdYh9
R
,YdYi9
R
,YeYe9,YeY f9
R
,
YeYg9
R
,YeYh9
R
,YeYi9
R
,Y fY f9
Y fYg9
R
,Y fY h9
R
,Y fYi9
R
,YgYg9
YgYh9
R
,YgYi9
R
,YhYh9,YhYi9
R
YiYi9
Figure 1: Rotation invariant features (3×3
R
, 5×5
R
, 7×7
R
and 9× 9
R
).
3 EXPERIMENTS AND RESULTS
This section describes (1) experimental textures, (2)
comparison of filters for various lengths, (3) similar-
ity retrievals of a texture database
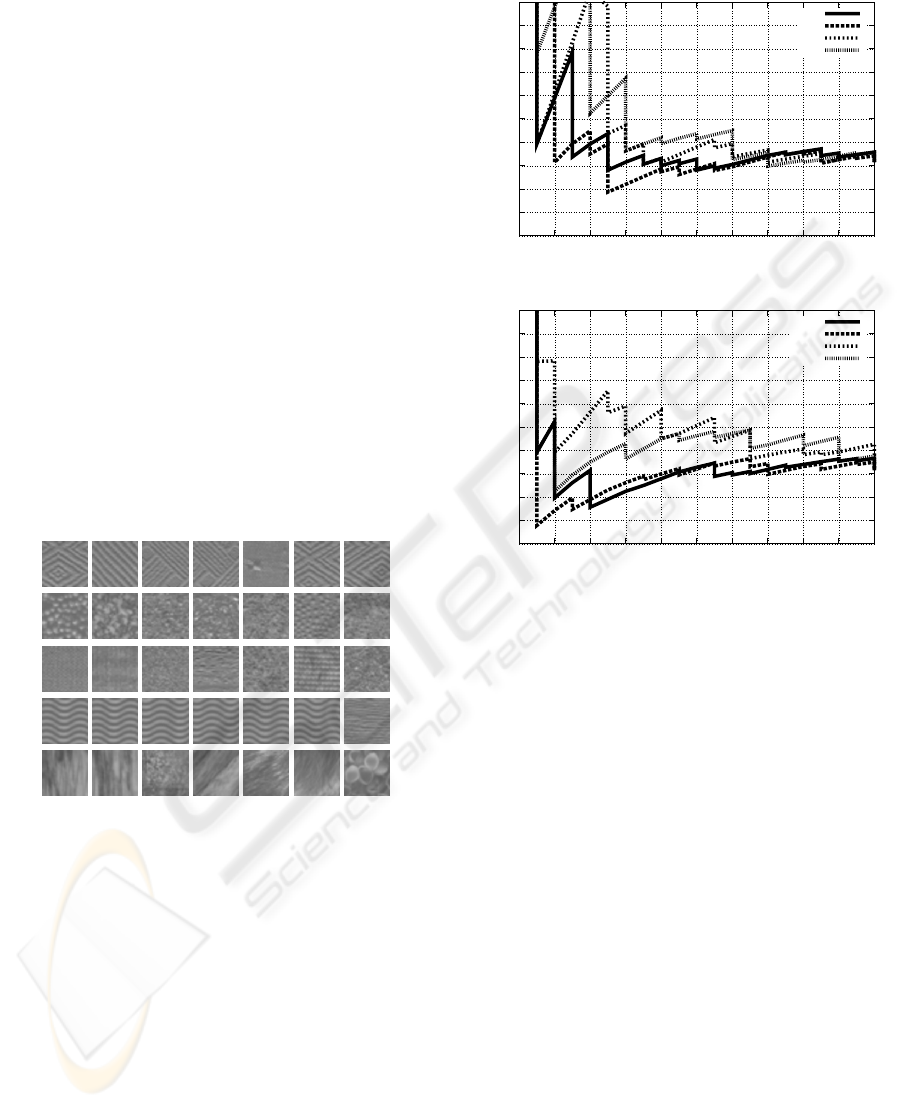
3.1 Experimental Textures
In our experiment, a portion of the OUTEX (Ojala
et al., 2002) texture database was used. It contains
6380 textures (Outex-TR-00000 data set). It consists
of 319 classes of textures with 20 textures in each
class. The database contains both macro-textures and
micro-textures. Texture sizes are 128 × 128 in RAS
image data format. In our experiments, these data are
converted to sizes of 128 × 128 images in PGM for-
mat with 65536 grey scale colors.
3.2 Comparison of Filters for Various
Lengths
Various lengths of Laws’ filters were examined to de-
termine whether the filters can classify the textures.
For the experiments, five classes of textures were se-
lected from a portion of the OUTEX database. The
examples of the textures are shown in Figure 2. Each
class contains 20 textures, thus there were a total of
100 textures. Figure 3 shows examples of convolved
texture images (seeds textures) using Laws’ filters
(3 × 3, 5 × 5 and 7 × 7). As the filter sizes are in-
creased, the resolutions of the convolved images be-
come coarser. Texture images analyzed by large size
filters such as 7 × 7 contain very similar convolved
texture images. Some features associated with these
similar convolved images are considered redundant,
and these convolved images can be eliminated for ef-
ficient computation. The elimination of the redundant
features avoids a bias from the features due to dimen-
sionality.
Once the entire texture data were analyzed by
Laws’ filters, the texture energycould be computed by
the technique mentioned in the previous section (Sec-
tion 2). For the texture energy computation, 15 × 15
smoothing windows were used for the experiments.
These texture energy values and texture class iden-
tification numbers were used as input of a discrim-
inant analysis (LDA). In this experiment, Laws’ fil-
ters of sizes 3 × 3, 5 × 5, 7 × 7 and 9 × 9 were ex-
amined. For each filter size, rotation invariant (men-
tioned in section 2.3) features (3× 3
R
, 5 × 5
R
, 7 × 7
R
and 9×9
R
) were also computed. Ten textures for each
class were used for the learning data sets (10 textures
× 5 classes).
A 2D TEXTURE IMAGE RETRIEVAL TECHNIQUE BASED ON TEXTURE ENERGY FILTERS
147

Seeds
Paper
Pasta
Figure 2: Example of textures.
Figure 4 shows texture data of discriminant co-
ordinates for features based on the Laws 7 × 7 filter.
Four discriminant functions are labeled LD1, LD2,
LD3 and LD4 in the figure. The labels a, b, c, d and
e in the figure indicate each class of textures. When
each function has good discriminating power, there is
no overlap observed between texture classes.
Figure 5 shows proportions of eigenvalues for the
discriminant functions. The eigenvalues reflect the
amount of variance explained in the grouping vari-
ables by the predictors. In the figure, the proportion
of the eigenvalues estimates the relative importance
of the discriminant functions. In the case of the fig-
ure, discriminant functions LD1, LD2, and LD3 have
more discriminating power compared to that of LD4.
The larger the coefficient values of a predictor in
the discriminant function, the more important its role
in the discriminant function. Therefore, these predic-
tors (image features) associated with the larger coef-
ficients are influential predictors (image features) for
classifying textures. In this example, features XeXe7,
X fXd7 and X fX f7 had relatively large coefficients
for the LD1 function, and they are considered as im-
portant image features for classifying our experimen-
tal texture dataset. Important image features vary de-
pending on the patterns which are contained in the
texture dataset.
Figure 6 shows a set of test texture data (tex-
tures of seeds) classified by the discriminant func-
tions trained by the training data set. In the figures,
rows represent predicted texture types, and columns
represent actual texture types. For the 5 × 5 filter
case, there are 4 textures misclassified. Two percent
(1/50) of ’a’ textures are misclassified as ’f’ textures,
2% (1/50) of ’b’ textures are misclassified as ’e’, 2%
(1/50) of ’d’ textures are misclassified as ’c’, and 2%
(1/50) of ’e’ textures are misclassified as ’d’, There-
fore, 92% (46 out of 50) of test textures are classified
Source texture image
1
2
3
3× 3
1
2
3
4
5
5× 5
1
2
3
4
5
6
7
7× 7
Figure 3: Examples of convolved texture images using
Laws’ filters (3× 3, 5× 5 and 7× 7).
correctly for the 5 × 5 filter. The classification rates
for each filter can be computed in a similar manner,
and the rates are shown in Figure 7. As shown in Fig-
ure 7, filters 5×5, 7×7, 7×7
R
, 9×9 and 9× 9
R
show
fair classification rates.
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
148

Figure 4: Texture data of discriminant coordinates for features of the 7× 7 filters.
LD1 LD2 LD3 LD4
0.5928 0.1757 0.1460 0.0855
Figure 5: Proportions of eigenvalues for discriminant func-
tions (7× 7 filters).
a b c d e
a 9 0 0 1 0
b 0 9 0 0 1
c 0 0 10 0 0
d 0 0 1 9 0
e 0 0 0 1 9
Figure 6: Classification rate tables for filters 5 × 5 (Seeds
textures).
3.3 Similarity Retrievals of a Texture
Database
Experiments on similarity retrievals of a texture
database have been conducted. The Laws’ filters
3×3 5 ×5 7×7 9×9
Seeds 42.0% 92.0% 100.% 96.0%
Paper 56.0% 90.0% 100.% 96.0%
Pasta 56.0% 86.0% 100.% 94.0%
3× 3
R
5× 5
R
7× 7
R
9× 9
R
Seeds 42.0% 62.0% 78.0% 100.%
Paper 38.0% 56.0% 90.0% 100.%
Pasta 30.0% 64.0% 94.0% 100.%
Figure 7: Classification rates for filters 3 × 3, 5× 5, 7× 7,
9× 9, 3× 3
R
, 5× 5
R
, 7× 7
R
, 9× 9
R
.
(3× 3, 5 × 5, 7 × 7 and 9 × 9) have been applied to
the database to extract texture image features. Also,
rotation invariant features (3× 3
R
, 5 × 5
R
, 7 × 7
R
and
9 × 9
R
) have been computed. The database contains
6380 textures (128× 128; 20 images × 319 classes),
A 2D TEXTURE IMAGE RETRIEVAL TECHNIQUE BASED ON TEXTURE ENERGY FILTERS
149
and the image feature extraction computation took
about six hours using a standard computer (Intel (R)
Core 2 Duo E8600 processor). The extracted fea-
tures were analyzed by principal component analysis
(PCA). The PCA transforms a number of correlated
features into a smaller number of uncorrelated fea-
tures called principal components. The PCA reduces
the dimensionality of the data set without a significant
loss of information. Since our image feature data sets
contain redundant features for higher resolution filters
such as 7 × 7 and 9 × 9, the redundant features can
be eliminated by applying the PCA. For our texture
retrieval system, the dimensions of the feature space
were reduced. All the dimensions of the feature space
were reduced so that the features kept over 90% of
their information.
The k-nearest neighbor algorithm (KNN) was
used for retrieving texture from the database. A tex-
ture was classified by a majority vote of its neighbors,
with the texture being assigned to the class most com-
mon amongst its k nearest neighbors.
Figure 8 shows examples of the similarity retrieval
of textures. In each figure, the six most similar tex-
tures determined by the system are shown.
1
2
3
4
5
Figure 8: Similarity retrieval of textures (In each figure, the
left image shows the query key).
Figure 9 shows a Recall-Precision graph for the
retrieval test. In the experiment, 20 random query
keys were selected, and corresponding recall rates and
precision rates were computed.
In the figure, filters 7× 7, 7× 7
R
, 9× 9 and 9× 9
R
show good retrieval results compared to other filters
when our experimental database is examined.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 10 20 30 40 50 60 70 80 90 100
Precision (%)
Recall (%)
Recall-Precision
3x3
5x5
7x7
9x9
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
0 10 20 30 40 50 60 70 80 90 100
Precision (%)
Recall (%)
Recall-Precision
3x3R
5x5R
7x7R
9x9R
Figure 9: Recall-Precision graph for the retrieval test.
4 CONCLUSIONS AND FUTURE
WORK
Two dimensional image textures were analyzed by the
Laws’ texture energy measure approach. Various res-
olutions of Laws’ filters (3× 3, 5× 5, 7× 7 and 9× 9)
were used for extracting image features. Also, ro-
tation invariant features (3 × 3
R
, 5 × 5
R
, 7 × 7
R
and
9×9
R
) were computed. A database of a texture image
was analyzed using a simulation software program. In
the experiments, classification rates of the Laws’ fil-
ters were evaluated, and textures were classified fairly
well when the filters were used in conjunction with
the discriminant analysis. A principal component
analysis (PCA) and a k-nearest neighbor (KNN) al-
gorithm were used for the similarity retrieval. Use of
these statistical techniques reduced unnecessary im-
age features, and made possible the retrieval of pat-
tern similar textures from the database.
For future experiments, additional 2D textures
which contain various patterns will be examined.
Other statistical approaches such as a quadratic dis-
criminant analysis will be applied in conjunction with
the Laws’ filters for improving classification rates.
IMAGAPP 2009 - International Conference on Imaging Theory and Applications
150

Also, other filtering techniques (Randen and Husoy,
1999) will be examined for content-based image re-
trieval.
ACKNOWLEDGEMENTS
This research was partially supported by grants
from the Telecommunications Advancement Foun-
dation, Japan (TAF-2007) and the KAKENHI (YR-
19700108).
REFERENCES
Chang, T. and Kuo, C. J. (1993). Texture analysis and clas-
sification with tree-structured wavelet transform. In
IEEE Trans. Image Process. 2 (4), pp.429–441.
Cross, G. and Jain, A. (1983). Markov random field texture
models. In IEEE Trans. Pattern Anal. Mach. Intell. 5
(1), pp.25–39.
Datta, R., Joshi, D., Li, J., and Wang, J. Z. (2008). Image
retrieval: Ideas, influences, and trends of the new age.
In ACM Computing Surveys, vol. 40, no. 2.
Haralick, R. M., Shanmugam, K., and Dinstein, I.
(1973). Textural features for image classification. In
IEEE Trans. Sysmtems Man Cybernetics,Vol.3, No.6,
pp.610–621. IEEE.
Kato, T. (1992). Database architecture for content-based
image retrieval. In Proc. SPIE Image Storage Re-
trieval System, 1662, pp.112–123.
Laws, K. I. (1979). Texture energy measures. In DARPA
Image UnderstandingWorkshop, pp.47–51. DARPA.
Laws, K. I. (1980). Rapid texture identification. In Im-
age Processing for Missile Guidance, SPIE Vol. 238,
pp.376–380.
Manjunath, B. and Ma, W. (1996). Texture features for
browsing and retrieval of image data. In IEEE Trans.
Pattern Anal. Mach. Intell. 18 (8), pp.837–842.
Ojala, T., Maenpaa, T., Pietikainen, M., Viertola, J., Kyllo-
nen, J., and Huovinen, S. (2002). Outex - new frame-
work for empirical evaluation of texture analysis algo-
rithms. Proc. 16th International Conference on Pattern
Recognition, Quebec, Canada, pp.701–706.
Randen, T. and Husoy, J. (1999). Filtering for texture clas-
sification: a comparative study. In Pattern Analysis
and Machine Intelligence, IEEE Transactions on Vol.
21, Issue 4, pp.291-310. IEEE.
Suzuki, M. T. and Yaginuma, Y. (2007). A solid texture
analysis based on three dimensional convolution ker-
nels. In Electronic Imaging 2007, Videometrics IX,
(EI-2007), Proc. of SPIE and IST Electronic Imaging,
SPIE Vol. 6491, 64910W pp.1–8.
Veltkamp, R. C. and Tanase, M. (2000). Content-based im-
age retrieval systems: A survey. In Technical Report
UU-CS-2000-34. Institute of Information and Com-
puting Science, University Utrecht.
A 2D TEXTURE IMAGE RETRIEVAL TECHNIQUE BASED ON TEXTURE ENERGY FILTERS
151
