EXPLOITING HUMAN BIPEDAL MOTION CONSTRAINTS

FOR 3D POSE RECOVERY FROM A SINGLE

UNCALIBRATED CAMERA

Paul Kuo, Thibault Ammar, Michal Lewandowski, Dimitrios Makris and Jean-Christophe Nebel

Digital Imaging Research Centre, Kingston University, London, U.K.

Keywords: 3D pose recovery, Orthographic projection, Pin-hole camera model, Camera auto-calibration, Biomechanics.

Abstract: A new method is proposed for recovering 3D human poses in video sequences taken from a single

uncalibrated camera. This is achieved by exploiting two important constraints observed from human bipedal

motion: coplanarity of body key points during the mid-stance position and the presence of a foot on the

ground – i.e. static foot - during most activities. Assuming 2D joint locations have been extracted from a

video sequence, the algorithm is able to perform camera auto-calibration on specific frames when the

human body adopts particular postures. Then, a simplified pin-hole camera model is used to perform 3D

pose reconstruction on the calibrated frames. Finally, the static foot constraint which is found in most

human bipedal motions is applied to infer body postures for non-calibrated frames. We compared our

method with (1) “orthographic reconstruction” method and (2) reconstruction using manually calibrated

data. The results validate the assumptions made for the simplified pin-hole camera model and reconstruction

results reveal a significant improvement over the orthographic reconstruction method.

1 INTRODUCTION

Recovery of 3D posture sequences provides

essential information for the analysis of human

behaviour and activity. Although computer vision

systems have been proposed, they either rely on

controlled environments involving several cameras

or are limited to specific human activities.

Therefore, they cannot be used in most real-life

applications, such as the detection of antisocial

behaviours from images captured from a CCTV

camera, where only data recorded by a single

uncalibrated camera are available. Consequently,

human pose recovery from a single uncalibrated

camera is still one of the major challenges facing the

computer vision community.

The goal of pose recovery is to localise a

person’s joints and limbs in either an image plan (2D

recovery) or a world space (3D recovery), which

usually results in the reconstruction of a human

skeleton. In this work, we concentrate on 3D pose

recovery. The success of pose recovery is measured

in terms of posture error，i.e. the average Euclidean

distance between corresponding joints of the

recovered and actual postures by aligning two bodies

with optimal scaling, translation, and rotation. This

metric reflects the real dissimilarity between two

postures.

In this paper, we propose a novel method for

estimating a 3D pose from 2D joint locations using a

single uncalibrated camera. Assuming 2D positions

of these key points have been extracted from a video

sequence, we are able to perform camera auto-

calibration for some key frames automatically

selected in the sequence (Kuo et al., 2007). This

exploits a human bipedal motion constraint that

certain body joints become coplanar within a motion

cycle. This provides sufficient knowledge for

reconstruction of a 3D figure in a world space using

a pin-hole camera model. In order to recover poses

for other frames, another human bipedal motion

constraint, i.e. the presence of a foot on the ground –

i.e. static foot - during most activities, is exploited to

propagate 3D posture reconstruction from one frame

to the next.

The structure of this paper is organised as

follows. After presenting relevant literature review,

we detail in Section 2 our pose recovery algorithm.

Then, experiments to validate our method with

quantitative results are given in Section 3. Finally,

conclusions and future work are addressed in

Section 4.

557

Kuo P., Ammar T., Lewandowski M., Makris D. and Nebel J. (2009).

EXPLOITING HUMAN BIPEDAL MOTION CONSTRAINTS FOR 3D POSE RECOVERY FROM A SINGLE UNCALIBRATED CAMERA .

In Proceedings of the Fourth International Conference on Computer Vision Theory and Applications, pages 557-564

DOI: 10.5220/0001821305570564

 SciTePress

1.1 Related Work

Since geometric camera calibration reveals the

relationship between the 3D space that is viewed by

the camera and its projection on the image plane, it

is a key for the reconstruction of a 3D articulated

structure. The common practice for calibrating

cameras is to obtain point correspondences between

a known calibration pattern and its projection on the

image (Tsai, 1987). Although such process is

straightforward, it is very often unpractical as

cameras often change position, their number may be

very large or physical access to them is impossible.

In order to deal with this issue, Taylor offered a pose

recovery method which does not require any camera

calibration (Taylor, 2000). He exploits an

orthographic projection model that assumes 3D

objects are very far away from the camera thus the

depth of their surface points are almost constant.

Although it has been widely used (Mori and Malki,

2002, Mori and Malki, 2006, Remondino and

Roditakis, 2003), as we shall see in our result

section, accuracy is compromised by such a strong

assumption. Inspired by Taylor’s work (Taylor,

2000), our method does not required any manual

camera calibration and relies on the location of 2D

image key points, i.e. joints, as an input. However, it

uses bipedal motion constraints to recover more

accurately 3D poses.

The extraction of 2D joint positions from an image

has been a very active field of research (Ren et al.,

2005, Kuo et al., 2008, Balan and Black, 2006,

Urtasun et al., 2006). Ren et al. extracts body

segments by exploiting parallelism and pairwise

constraints of the body parts (Ren et al., 2005). Kuo

et al. extended this approach by adding other image

cues, i.e. colour and motion, which are informative

regarding body part location (Kuo et al., 2008).

Others use a Wandering-Stable-Lost framework to

track 2D body parts/key points through the

sequences (Balan and Black, 2006, Urtasun et al.,

2006).

Most pose reconstruction methods rely either on

multiple cameras (Bhatia et al., 2004, Izo and

Grimson, 2007), and/or assume specific types of

activities (Bhatia et al. 2004, Elgammal and Lee,

2006, Tian et al., 2004, Lim et al., 2006, Ek et al.,

2008). Moreover, some of them require manual

initialisation of their 3D tracker (Balan and Black,

2006, Urtasun et al., 2006, Martinez-del-Rincon et

al., 2008). Therefore, all these constraints

dramatically limit the practical applications of those

systems.

Our approach exploits general constraints

imposed by human bipedal motion. They include the

presence of at least one foot on the ground during

most activities; this constraint has already been used

successfully in 2D body tracking (Martinez-del-

Rincon et al., 2008). These bipedal constraints are

much less restricting than assuming a specific type

of motions (e.g., walking). In this work, we use such

constraints for camera self-calibration from

observing human motion to derive 3D poses for key

frames (Kuo et al., 2007) and further infer 3D poses

between key frames.

2 METHODOLOGY

2.1 3D Human Pose Recovery

Our goal is to recover 3D human postures in video

sequences by exploiting human bipedal motion

constraints. We propose a 3D pose estimator which

generates possible 3D poses from 2D joint positions

in the input image sequence. Then the most proper

pose is selected by taking into account learned

human motion models. Figure 1 illustrates the flow

of our 3D human pose recovery. It requires an image

processing task of detection of “image key points”

related to postures i.e., 2D body joints, from the

video. The 3D pose estimator, which is based on

pin-hole projection, then transforms 2D images

points to a set of 3D poses in real world, using the

constraints of human bipedal motion. Based on the

motion models which are learnt from dynamics and

further constraints of human motion, the most likely

pose can be selected among the proposed 3D poses.

Because the task of obtaining key body points

from the image has been tackled in our previous

paper (Kuo et al., 2008) and a paper dealing with

pose selection is in preparation, in this work, we will

concentrate on the 3D pose estimator which covers

the pose reconstruction by exploiting human bipedal

motion constraints.

2.2 3D Pose Estimator

The 3D pose estimator generates a set of 3D pose

proposals from 2D joint positions based on the pin-

hole projection model. First, postures are estimated

automatically for a set of key frames where camera

auto-calibration can be performed. Then, the other

postures are recovered by propagating the

parameters of the pin-hole projection model

obtained for the key frames to other frames by

introducing a constraint of bipedal motion.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

558

Figure 1: 3D pose recovery pipeline.

The key frames are specific frames when the

human body adopts particular postures where five

points are coplanar. Using those points a coplanar

calibration model can be used to estimate the camera

parameters (Tsai, 1987).

Figure 2 shows an in-depth insight of the 3D pose

estimator. Firstly the sequence with extracted key

body points is used to perform “camera auto-

calibration” (see Section 2.2.1). This is an iterative

process to select the key frames and to estimate

calibration parameters, i.e. focal length and camera

relative position. This also generates a 3D coplanar

model representing the 3D configuration of the set

of coplanar body joints at key frames (Figure 3).

Secondly, the pin-hole projection model is

employed to reconstruct 3D postures for the

calibrated key frames. The projection line of each

key body point on the image can be established

using the estimated focal length. Their

corresponding 3D points can be located on the

projection lines according to the camera relative

position and the body model. The body model is a

3D skeletal representation of a human body (see

Figure 3) which consists of 15 joints: shoulders,

hips, shoulder centre, hip centre, elbows, hands,

knees, feet and a head. It is constructed from the

calibrated 3D coplanar model with known body

ratios. Since this problem is ill-constrained

(

ℜ→ℜ

), multiple postures are generated. A pose

selection mechanism is then required to extract the

correct posture. The pin-hole based reconstruction

will be detailed in Section 2.2.2.

Finally, to recover postures for non-key frames,

the bipedal constraint of the static foot is used.

Human biomechanics reveals that at any moment at

least one foot is in contact with the ground in most

types of bipedal motion. This static foot exists

because the body requires at least one limb to

support its weight. Motion is achieved by switching

weight support to the other foot. Both feet can only

be off ground for a short moment if any, e.g.

running. This static foot constraint can be exploited

for pose recovery, since knowledge of the 3D

posture at one frame also provides the 3D

coordinates of one foot in the next frame. Therefore,

postures can be propagated from the reconstructed

key frames to their neighbouring frames. The detail

of this posture propagation using a static foot will be

discussed in Section 2.2.3.

Parame

ers

Figure 2: Details of 3D pose estimator.

Figure 3: Body model (red) and key points of the coplanar

model (green circles).

2.2.1 Camera Auto-Calibration

In order to perform 3D pose reconstruction based on

pin-hole projection, it is necessary to estimate the

camera calibration parameters. In order to make this

task automatic, the camera model needs to be

simplified. We assume the principal axis goes

EXPLOITING HUMAN BIPEDAL MOTION CONSTRAINTS FOR 3D POSE RECOVERY FROM A SINGLE

UNCALIBRATED CAMERA

559

through the centre of the image and there is neither

lens distortion nor skew. The validity of these

assumptions will be accessed in our result section.

The required projection parameters are the focal

length and the camera relative position to the body.

They are estimated by using the camera auto-

calibration method proposed in (Kuo et al., 2007).

This can summarised as follows. It is based on

Tsai’s coplanar calibration method (Tsai, 1987)

where a set of 3D coplanar points and their projected

locations on the image plane are required. A study of

human biomechanics reveals that the shoulders and

hips are expected to be coplanar at some time during

a cycle of bipedal motion, i.e. mid-stance position.

As a result, key points on (but not limited to) the

shoulders and hips are suitable for coplanar

calibration. Therefore, the automatic identification

of the coplanar instances and the 3D structure of the

key points can achieve camera auto-calibration. The

core of this auto-calibration method lies on the

observation that a smaller variation of the focal

length estimates indicates the smaller error in

coplanarity of the key points and the 3D coplanar

model, which results in more accurate calibration.

Tsai’s coplanar calibration estimates the focal length

by solving an over-determined linear system, which

yields 10 estimates of the focal length. The variation

of these 10 estimates is used in (Kuo et al., 2007) to

reflect errors in coplanarity and 3D representation of

the key points. Therefore, the key frames and the

coplanar model (which is part of the body model)

can be selected by minimising standard deviation of

the focal length estimates through frames of the

sequence and coplanar model space. Apart from the

key frames and a coplanar model being identified,

focal length and the camera relative position to the

body in terms of rotation and translation parameters

are also estimated from this auto-calibration process.

Since the coplanar model has been identified, a body

model is built using the shoulder length, hip length

and spine length which are extracted from the

coplanar model to estimate the size of the limbs

(lower/upper arms/legs) and the head (Figure 3).

2.2.2 3D Human Body Reconstruction using

Pin-Hole Projection Model

The pin-hole projection model, as illustrated in

Figure 4, is employed for 3D pose reconstruction.

This method relies on the determination of the

projection line of each image point. Then, along the

projection line the corresponding 3D point needs to

be localised using the known distances between its

neighbouring points as a constraint. This can be

achieved using the parameters estimated from auto-

calibration, i.e., focal length, camera relative

position and the body model. Since the 3D positions

of shoulder and hip points were already estimated in

the calibration process – they form the required 3D

coplanar model - (see Section 2.2.1), only limbs

(upper/lower arms/legs) and the head need to be

reconstructed. Their positions are calculated piece-

wisely from the points of the coplanar model (i.e.,

shoulders or hips) towards the limbs’ distal ends, by

applying Equation (1).

)1(,1

=−−

−− tttt

LPP

(1)

0)(cos2

)1(,

=−+−

−−

−

ttt

LDDDD

(2)

Where P

t-1

is a 3D body key point (e.g., the left

shoulder, P

l_shdr

, see Figure 4) whose coordinates are

already known, and P

is the point which is to be

reconstructed (e.g., the left elbow, P

l_elb

, see Figure

4). L

t,,(t-1)

is the expected segment length between

two successive key points.

and P

t-1

’s projection lines can be established

by connecting the optical centre, O, and their

corresponding image points, p

and p

t-1

. Since P

constrained on its projection line, its location can be

computed by using Equation (2) which considers the

trigonometry of the triangle

△

O- P

t-1

-P

. D

and D

t-1

denotes the distance of P

to O

and

t-1

to O;

θ is the

angle between these two projection lines (see Figure

4). Since D

t-1

, θ and L

t,(t-1)

are known, D

can be

solved to locate P

. As the problem is ill-constrained

(

ℜ→ℜ

), the quadric formulation of Equation (2)

gives us two P

locations. This is because it cannot

distinguish, from a 2D image point, whether the

corresponding 3D point is closer or further away

from the camera than its neighbouring point, unless

some depth information is provided. As a

consequence, a number of 2

poses will be

generated (5 coplanar points have been located

uniquely by the calibration). The pose selection (see

Figure 1) will then determine the most proper 3D

posture for this frame among these pose proposals.

To evaluate our reconstruction, in this paper, we

assume pose selection is a solved problem.

2.2.3 Reconstruction Propagation using

Static Foot Points

The propagation of 3D reconstruction relies on the

static foot constraint which is observed in most

bipedal motions where generally at least one foot

stays on the ground to support body weight.

Identification of static foot locations in a sequence is

the key to propagate the estimated postures from the

key frames to non-key frames. The 3D coordinates

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

560

Figure 4: Pin-hole projection model for 3D pose

reconstruction applied to the reconstruction of the left arm.

of a stationary key point identified in a previous

frame is used as the starting point of pin-hole pose

reconstruction for the current frame. Walking, as an

example, requires that one leg always stays on the

ground while the other is swinging and there is a

short period of “double support” during which the

legs exchange the motion. Therefore the posture can

be propagated continuously from one static foot to

the other via the “double support” period. This

posture propagation can also be used in motions

which contain “off-ground” moments (such as

running or dancing) where pose interpolation is

required to fill the temporal gaps.

The static foot can be identified effectively and

accurately by comparing speed of foot points

between consecutive frames. Equation 3 makes a tri-

nary decision (left foot, right foot or none) of the

static foot for the current frame I

by computing the

displacement of the left and right feet between the

previous and next frames, I

t-1

and I

t+1

. I

t-1

(x, y),

t+1

(x, y), I

t-1

(x, y) and I

t+1

(x, y) denote the

locations of the left and right foot points in the

previous and next frames and Euclidean distance is

used to compute the displacement between two 2D

points. If the displacement of the right foot is greater

than the left one, the left foot is determined as the

static foot (i.e., SF(t)= left foot) and vice versa,

provided the speed of the foot is below a threshold,

Thr.

),(),(),(),()(

1111

yxIyxIyxIyxItD

+−+−

−−−=

If (D(t)<0 && |I

t-1

(x, y)- I

t+1

(x, y)|<Thr)

SF(t) =left foot

else if (D(t)>0 && |

t-1

(x, y)- I

t+1

(x, y)|<Thr)

SF(t) = right foot

else

SF(t) = None

(3)

If a static foot is identified, the pin-hole

reconstruction (see Section 2.2.2) can be performed

for non-key frames. This is a recursive process that

propagates the postures from the key frames in both

forward and backward directions in time. In each

direction, we firstly reconstruct the frame next to the

key frames whose static foot 3D position has been

identified so that it can be used as a seed of the pin-

hole reconstruction for this frame. The

reconstruction starts from the static foot 3D point

and estimates the 3D positions of the keen and hip of

the same leg. It then estimates the 3D position of

another leg, and followed by the spin, shoulders,

head and arms. Once this frame is reconstructed, its

static foot position can be passed on to its adjacent

frame that will be reconstructed in the same manner.

Since there are multiple key frames within a given

sequence, a linear combination of the propagated

postures from each key frame is calculated to

generate the final one. Weights are introduced to

penalise postures which are temporally further away

from their key frames.

3 EXPERIMENTAL RESULTS

3.1 Dataset and Experimental Settings

The algorithm was tested on the HumanEva (HE)

dataset (

http://vision.cs.brown.edu/humaneva), which is

used as benchmark for pose recovery. It provides

motion capture and video data which were collected

synchronously. Therefore, motion capture data

provide 3D ground truth of human poses: since

cameras are calibrated, 3D data points can be

projected on the image plane so that 2D locations of

key body points in the sequences are available for

pose recovery algorithms. Moreover, a standard set

of error metrics is defined to evaluate pose

estimations (Sigal and Black, 2006).

To validate our proposed method, two other pose

recovery techniques are also evaluated:

Reconstruction using orthographic projection

(Taylor, 2000),which is one of the most popular 3D

pose recovery method for uncalibrated cameras, and

pin-hole reconstruction using the calibration data

and body model directly provided by the HE. In

order to validate the assumption made for our

simplified camera model, in the later case, we

neglect lens distortion and skew, and set the image

centre as the principal centre. To make an unbiased

comparison between these two methods and our

proposed method, all experiments are conducted

with known body ratio (this is obtained from the

HE) and known depth relations between pairs of key

EXPLOITING HUMAN BIPEDAL MOTION CONSTRAINTS FOR 3D POSE RECOVERY FROM A SINGLE

UNCALIBRATED CAMERA

561

points, i.e. front or back, as a substitute for the pose

selection.

A sequence of “walking in a circle”-- S2 Walking

(C1) in the HE-- is selected as a testing sequence.

Since the original sequence is quite long, only one

complete walking circle is used, i.e. frame 340 to

760. The sequence was chosen to include a variety

of walking postures, i.e. a complete circle, seen from

different distances and view angles.

3.1.1 Orthographic Reconstruction

This method proposed by Taylor (Taylor, 2000)

does not require calibration since it assumes the

object to be reconstructed is far away from the

camera so that the Z coordinates (the depth) are

almost constant for all the points on the object. Since

this method requires the user selects a suitable

scaling factor, it only recovers the posture (i.e.,

relative positions of the key body points), but not the

actual size of the human subject. Therefore,

Procrustes Analysis (Seber, 1984) is performed to

facilitate the comparison between the reconstructed

body and the motion capture data, which is our

ground truth. Procrustes Analysis determines a linear

transformation (translation, rotation, and scaling) of

the reconstructed body to best match to the ground

truth by minimising Root-Mean-Square error

(RMS). Reconstruction errors of this method are

showed in Figure 6 (blue) and Table 1 (first

column).

3.1.2 Pin-Hole Reconstruction using

Parameters Supplied from the Dataset

To validate the assumption of the simplified

calibration model used in the proposed method,

poses are reconstructed using the pin-hole projection

model with a number of parameters directly

provided from the HE dataset. These include camera

calibration parameters, i.e. focal length, camera

relative position to a key point of the subject (the

shoulder centre), subject’s body model and relative

depth information of adjacent points. Lens distortion

and skew are not considered, and it is assumed the

principal axis of the camera goes through the centre

of the image. As a result, the pin-hole reconstruction

can be seeded from the known shoulder centre.

Positions of the other key points are obtained by

using projection lines and by taking into account the

body model and relative depth information.

Procrustes Analysis is performed to allow

comparison with motion capture data. The results of

this method is showed in Figure 6 (red) and Table 1

(second column)

3.2 Evaluation of Pose Reconstruction

The auto-calibration process identified four key

frames, frame 359, 529, 614, 693, within the target

walking circle (See Figure 7 for original key frame

postures). Thus, their postures were estimated and

propagated to other frames using identified static

foot points. The final posture estimates are produced

by combining propagated poses produced by each

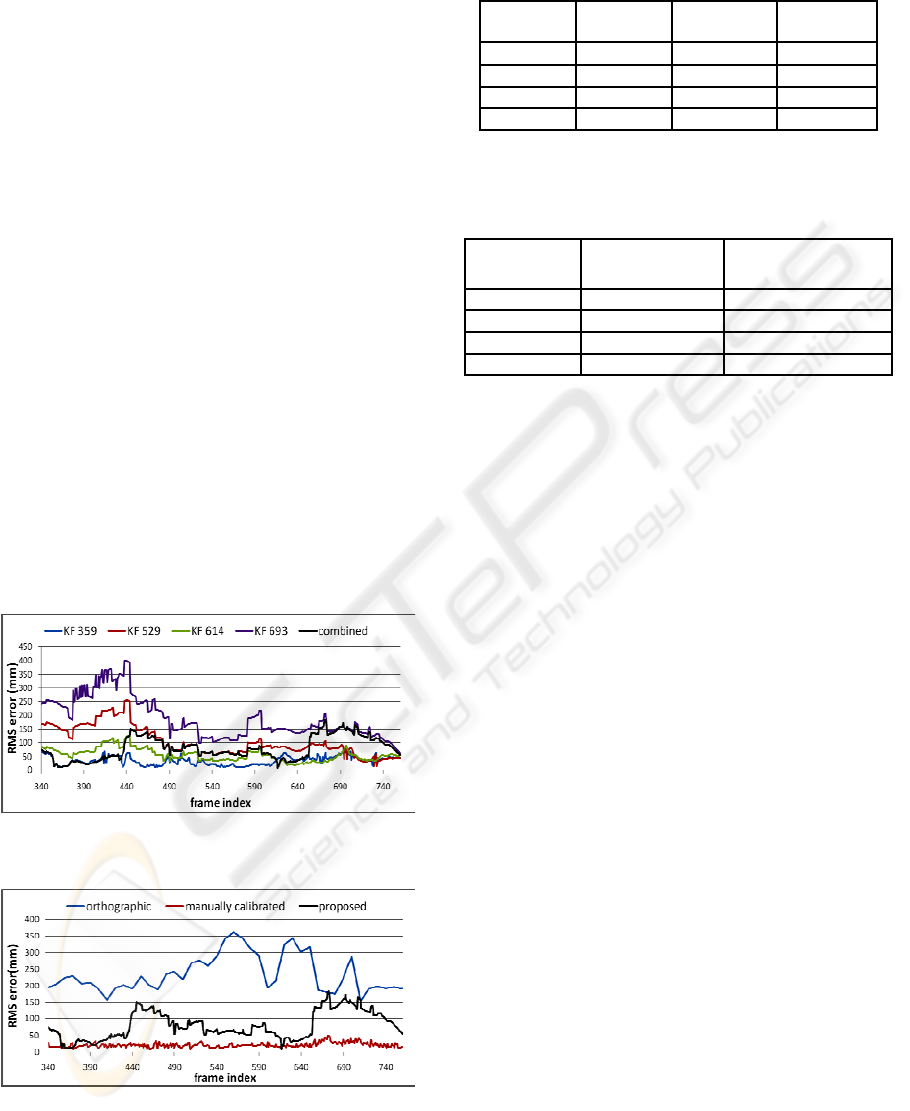
key frame as described in Section 2.2.3. Figure 5

shows the RMS errors of propagated postures from

each key frame and their combined postures.

Figure 6 and Table 1 show a comparison of our

proposed method with the reconstructions described

in Section 3.1.1 and 3.1.2. The result of the pose

estimation based on manual calibration (Section

3.1.2) produces an average error of 20.5 mm. This

validates the assumption of the simplified pin-hole

projection model used in our proposed method.

Also, since it is manually calibrated, it is considered

as the optimal result we could obtain in our method.

As shown in Figure 6, our proposed method (black)

clearly outperforms the orthographic reconstruction

(blue); the average error is reduced by two-third

(from 235.8 mm down to 79.5 mm, Table 1).

Statistical analysis in Table 1 also indicates our

method has reasonable accuracy (average error 79.5

mm) and is consistent (standard deviation is 41.7

mm). We also compare our results with the state-of-

the-art; (Husz et al., 2007) worked on similar

scenarios (single uncalibrated camera with

unspecified action) and an average error of 200 mm

was reported. Elgammal and Lee (2006) was able to

achieve 30 mm error on tracking joints in the same

sequence. However, their method is activity specific

(walking) and requires such motion to happen

cyclically. Further analysis of reconstruction of each

key frame and its posture propagation is shown in

Table 2. We notice the reconstruction and

propagation of the key frame 693 is significantly

worse than other key frames. Since the posture of

this key frame is approximately parallel to the image

plane (see Figure 7), it results in unreliable coplanar

calibration as shown in (Kuo et al., 2007).

Moreover, the reconstruction is further deteriorated

by lens distortion as the subject is positioned near

the border of the image in this frame.

Due to the limited space of the paper, Figure 7

illustrates only a subset of our reconstructed poses

against the ground truth. We show the reconstruction

of 4 key frames and other poses with a variety of

view angles and distances, including the difficult

cases where the subject is near the image border or

the posture is parallel to image plane.

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

562

4 CONCLUSIONS

In this paper, we presented a novel 3D pose recovery

algorithm by exploiting human bipedal motion

constraints using images from a single uncalibrated

camera. The algorithm can estimate camera

calibration parameters from a number of frames (i.e.,

key frames) in the sequence automatically,

reconstruct the key frames’ postures using a

simplified pin-hole camera model and infer postures

for other frames. To achieve this, two constraints

observed from human bipedal motion were used.

One is the coplanarity of the body points in the mid-

stance position to perform camera auto-calibration

and the other refers to the static point of the foot that

allows pose propagation from one frame to next.

Our method was validated experimentally. Results

showed an accuracy of 8 cm, which is usually

sufficient to label poses for action recognition

applications.

We plan to use 2D feature detectors and trackers

to localise the joints on real video sequences to test

further our method against noisy feature locations.

We will also incorporate a pose selection module

which embeds human motion dynamics and

constraints to select the most plausible posture

among the generated 3D pose proposals.

Figure 5: RMS error of our proposed pose recovery

algorithm.

Figure 6: RMS errors of 3 pose reconstruction algorithms.

Table 1: Statistical results of 3 reconstruction algorithms.

error(mm)

ortho‐

graphic

manually

calibratedproposed

average 235.8 20.5 79.5

max. 363.1 50.0 182.8

min. 153.3 8.0 7.4

s.d. 57 6.9 41.7

Table 2: Statistical results of key frame reconstruction and

propagation.

keyframe

reconstruction

error(mm)

Averageerror(mm)

inpropagation

359 23.0 35.5

529 67.4 106.3

614 46.3 58.0

693 172.4 189.6

REFERENCES

P. Kuo, J.-C. Nebel and D. Makris. Camera Auto-

Calibration from Articulated Motion, AVSS: pp. 135-

140. 2007.

R.Y. Tsai, A versatile camera calibration technique for

high accuracy 3D machine vision metrology using off-

the-shelf TV cameras and lenses, IEEE Journal of

Robotics and Automation, vol. RA-3 pp323-343 Aug,

1987.

C. J. Taylor. Reconstruction of Articulated Objects from

Point Correspondences in a Single Image, CVPR: pp.

677-684. 2000.

G. Mori and J. Malki. Estimating Human Body

Configurations using Shape Context Matching, ECCV,

LNCS 2352, vol. 3, pp. 666–680. 2002

G. Mori and J. Malki. Recovering 3D Human Body

Configurations Using Shape Contexts, IEEE Tran.

PAMI, vol.28. pp. 1052-1062. 2006

F. Remondino and A. Roditakis. 3D Reconstruction of

Human Skeleton from Single Images or Monocular

Video Sequences. 25th Pattern Recognition

Symposium, Lecture Notes in Computer Science,

Springer, DAGM 03, pp. 100-107. 2003

X. Ren, A.C. Berg and J. Malik. Recovering human body

configurations using pairwise constraints. ICCV: pp.

824-831. 2005

P. Kuo, D. Makris, N. Megherbi and J.-C. Nebel.

Integration of Local Image Cues for Probabilistic 2D

Pose Recovery", 4th International Symposium on

Visual Computing (ISVC), Springer-Verlag. 2008

A.O. Balan and M.J. Black. An Adaptive Appearance

Model Approach for Model-based Articulated Object

Tracking. CVPR: pp. 758-765. 2006.

R. Urtasun, D.J. Fleet and P. Fua. 3D People Tracking

with Gaussian Process Dynamical Models. CVPR:

pp.238-245. 2006.

EXPLOITING HUMAN BIPEDAL MOTION CONSTRAINTS FOR 3D POSE RECOVERY FROM A SINGLE

UNCALIBRATED CAMERA

563

Frame 359 Frame 529 Frame 614 Frame 693 Frame 393 Frame 450 Frame 555 Frame 653 Frame 742

(rms =23.0) (rms =67.4) (rms =46.3) (rms =172.4) (rms =21.2) (rms =

143.3) (rms = 62.6) (rms = 54.7) (rms = 92.9)

Figure 7: Reconstruction results; first row: frame index; second row: associated posture error, (Root-Mean-Square error in

mm); third row: original images; forth row: reconstructed (solid) and ground truth (dotted) postures observed from the

original viewpoint; fifth row: reconstructions observed from a novel viewpoint. The first 4 images are the key frames;

Frame 693 and 450 show poor reconstructions where the subject is located near the borders of the image.

S. Bhatia, L. Sigal, M. Isard and M.J. Black. 3D Human

Limb Detection using Space Carving and Multi-View

Eigen Models. CVPR: pp. 17-24. 2004.

T. Izo and W.E.L. Grimson. Simultaneous pose recovery

and camera registration from multiple views of a

walking person. Journal of Image and Vision

Computing: pp. 342-351. 2007.

A. Elgammal and C.S. Lee. Body Pose Tracking from

Uncalibrated Camera using Supervised Manifold

Learning. NIPS. 2006.

T. P. Tian, R. Li and S. Sclaroff. Articulated Pose

Estimation in a Learned Smooth Space of Feasible

Solutions. CVPR: pp: 50-57. 2005.

H. Lim, V. I. Morariu, O.I. Camps, M. Sznaier. Dynamic

Appearance Modeling for Human Tracking. CVPR: pp:

751-757. 2006.

C.H. Ek, P.H.S. Torr and N.D. Lawrence. Gaussian

Process Latent Variable Models for Human Pose

Estimation. LNCS 4892. Springer. pp: 132-143. 2008.

J. Martinez-del-Rincon, J.-C. Nebel, D. Makris, C. Orrite-

Urunuela. Tracking Human Body Parts Using Particle

Filters Constrained by Human Biomechanics. BMVC

2008.

http://vision.cs.brown.edu/humaneva. HumanEVA dataset,

Brown University.

L. Sigal and M. J. Black, HumanEva: Synchronized video

and motion capture dataset for evaluation of

articulated human motion, Tech. Report CS0608,

Brown Univ. 2006.

G. A. F. Seber. Multivariate Observations, Wiley, 1984.

Z. Husz, A. Wallace and P. Green, Evaluation of a

Hierarchical Partitioned Particle Filter with Action

Primitives. CVPR 2

workshop on EHuM

. 2007

VISAPP 2009 - International Conference on Computer Vision Theory and Applications

564