PYRAMIDAL MULTI-VIEW PBR

A Point-based Algorithm for Multi-view Multi-resolution Rendering of Large Data

Sets from Range Images

Sajid Farooq and J. Paul Siebert

Computer Vision and Graphics Lab, Dept of Computer Science, University of Glasgow, Glasgow, U.K.

Keywords: Multi-view integration, Point-based Rendering, Display Algorithms, Viewing Algorithms, Stereo-

photogrammetry, Stereo-capture.

Abstract: This paper describes a new Point-Based-Rendering technique that is parsimonious with the typically large

data-sets captured by stereo-based, multi-view, 3D imaging devices for clinical purposes. Our approach is

based on image pyramids and exploits the implicit topology relations found in range images, but not in

unstructured 3D point-could representations. An overview of our proposed PBR-based system for

visualisation, manipulation, integration and analysis of sets of range images at native resolution is presented

along with initial multi-view rendering results.

1 INTRODUCTION

3D images have the potential to provide clinicians

with an objective basis for assessing and measuring

3D surface anatomy, such as the face, foot or breast.

Clinicians often resort to subjective measures that

rely on naked eye observations, and carry out

surgical decisions based upon that data. Today, 3D

scanned images of patients can provide objective

metric measurements of body surfaces to sub-

millimetre resolution. Commercially available

stereo-photogrammetry capture systems such as

C3D (Siebert & Marshall, 2000) are capable of

capturing 3D scans up to 16 megapixels in

resolution. Although stereo-photogrammetry

systems are desirable for many reasons, they present

their own challenges. Large sets of data are difficult

to manage, process, and visualize. In addition, stereo

systems capture data from multiple ‘pods’ (each pod

consisting of a pair of cameras) around the object,

resulting in several 2.5D captures, each with a

partial view of the object. Hence, multi-view

integration techniques are usually required to join

these partial views into a single 3D representation.

The goal of this paper is to present progress towards

a multi-view, multi-resolution method that permits

clinicians to visualise, manipulate, measure and

analyse large 3D datasets at native imaging

resolution depicting 3D surface anatomy.

Traditionally, the most popular data

representation method for displaying 3D data has

been the 3D polygon. Large data sets, such as

captured by stereo imaging devices, however, are so

dense that polygon numbers must be reduced by

means of mesh decimation, increasing the size of the

remaining polygons and thereby losing resolution. In

order to achieve 3D visualisation at native imaging

resolution, it is more efficient to treat each 3D

(2.5D) measurement as a Point rendering primitive

(Levoy and Whitted, 1985) than attempt to render

polygons. Large data sets converted to polygons also

claim more memory than storing each individual

point (as regular range images for example).

Polygons are a notoriously difficult representation

when it comes to multi-view integration. Marching-

cubes (Lorenson and Cline, 1987) is a popular

algorithm, however, it rarely works seamlessly with

very high-resolution models. The standard

techniques, Marching-cubes (Lorenson and Cline,

1987), Zippered Polygon Meshes (Turk, Levoy,

1994), all suffer a loss of resolution at the seams,

and provide unpredictable results when polygonal

resolution approaches pixel size. In light of the

problems with polygon rendering methods, point-

based rendering (PBR) techniques have steadily

been gaining interest.

211

Farooq S. and Siebert J.

PYRAMIDAL MULTI-VIEW PBR - A Point-based Algorithm for Multi-view Multi-resolution Rendering of Large Data Sets from Range Images.

DOI: 10.5220/0001823602110216

In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications (VISIGRAPP 2009), page

ISBN: 978-989-8111-67-8

2 PREVIOUS WORK

The idea of using Points as a rendering primitive

was reported by Levoy and Whitted as far back as

1985 (Levoy and Whitted, 1985). The most common

Point-Based Rendering implementation currently in

use is Surface Splatting (Zwicker et al. 2001), where

a 3D object is represented as a collection of surface

samples. These sample points are reconstructed,

low-pass filtered and projected onto the screen plane

(Räsänen, 2002). Many extensions have been

proposed for Surface Splatting since their

introduction. Among others, Splatting has been

extended to handle multiple views (Hübner et al.

2006).

Rusinkiewicz and Levoy describe QSplat, a

system for representing and progressively displaying

meshes that combines a multi-resolution hierarchy

based on bounding spheres with a rendering system

based on points. A single data structure is used for

view-frustum culling, back-face culling, level-of-

detail selection, and rendering (Rusinkiewicz and

Levoy, 2000).

Both QSplat and Splatting techniques, however,

have their limitations. QSplat, while efficient, relies

on triangulated mesh data as input rather than native

Point data, and lacks anti-aliasing features. Splatting,

on the other hand, discards connectivity information

that is vital in a clinical context for measurement and

analysis of the underlying data.

Several multi-view integration approaches have

been proposed. Hubner et al (2006) introduce a new

method for multi-view Splatting based on deferred

blending. Hilton et al (2006), on the other hand, take

the traditional 'polygonization' approach by

proposing a continuous surface function that merges

the connectivity information inherent in the

individual sampled range images and constructs a

single triangulated model. Problems with both

Splatting techniques, and polygon approaches have

been mentioned earlier, making either multi-view

technique less than ideal for clinical purposes.

Image pyramids were introduced by Burt and

Adelson (1983a) as an efficient and simple multi-

resolution scale-space mage representation. Image

pyramids, in addition to providing a multi-resolution

algorithmic framework, have found use in down-

sampling images smoothly across scale-space.

Image pyramids, although 2D in nature, were

extended by Gortler et al (1996) in the landmark

Lumigraph paper where they discuss the ‘pull-push’

algorithm. The latest use of the image pyramid in

PBR techniques, and one that is closest to our work,

is that of Marroqium et al (2008). They implement

the image pyramid on the GPU to provide an

accelerated, multi-resolution, Point Based Rendering

algorithm based on scattered one-pixel projections,

rather than Splats as proposed by Zwicker et al

(2001).

Existing techniques, despite making use of range

images, and/or image pyramids, have not made the

combined use of the connectivity information

provided by the former, and the multi-resolution

capabilities provided by the latter, to provide a

multi-resolution, multi-view PBR algorithm that

could be used in a clinical setting for measurement

and analysis. We propose a method that takes range

images as its input, uses an image pyramid for

down-sampling, and smoothly joining multiple

views in image space via a multi-resolution Spline

as proposed by Burt et al (1983b), and finally,

projects the image using 3x3 pixel Gaussian kernels

for sub-pixel accurate, anti-aliased rendering.

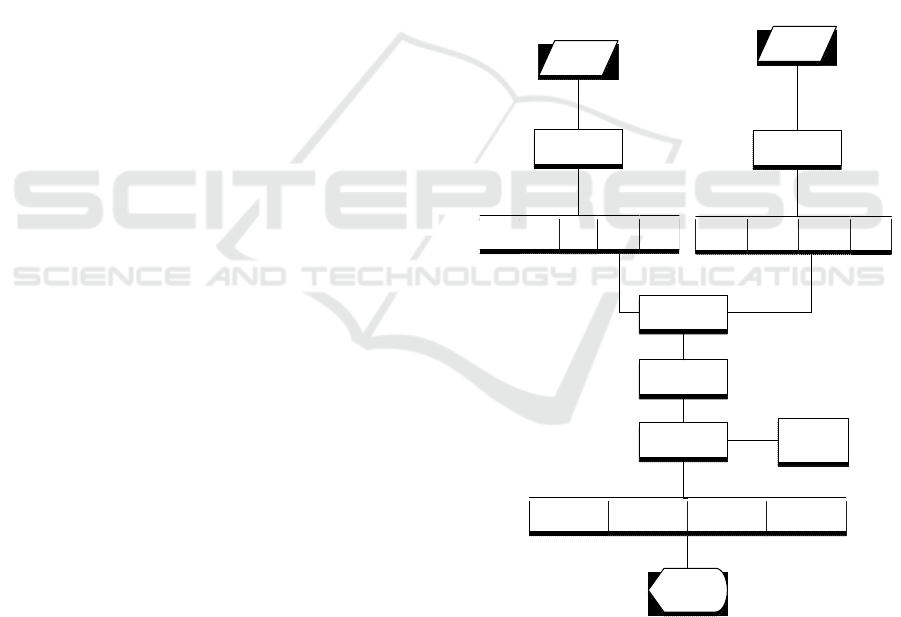
Texture

Image

Conversion to

Laplacian Image

Pyramid

Gauss

ian

Level

n-1

Level

n-2

Level

Transform from

Range to World

Space

Apply viewing

transformations

Project

Orthographically

onto screen

Rendered

Gaussian

Image

Rendered

Laplacian Level

n-1

Rendered

Laplacian Level

n-2

Rendered

Laplacian Level

Reconstruct

Pyramid

Range

Image

Conversion to

Gaussian Image

Pyramid

Level n Level n-1 Level n-2

Level

Gaussian

LUT

Figure 1: Overview of the rendering process for a single

view.

The advantage of using range images, coupled

with a PBR approach, is that our method renders

data at its native resolution, retains connectivity

information for measurement purposes, and provides

a matrix-like data-structure that is compact and ideal

for GPU acceleration.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

212

3 THE PROPOSED METHOD

The proposed method uses image pyramids, range

images and the Gaussian kernels to provide anti-

aliased, hole-free, multi-resolution 3D images. A

high-level overview of the algorithm, for a single

view, is as follows.

The input range image, provided in our case by a

stereo-photogrammetry capture system, is first

converted into a Gaussian Pyramid to provide

several range images, at subsequently smaller

resolutions. Since the range images together

comprise 3D data, this effectively provides anati-

aliased models at several resolutions. The

corresponding texture image is converted into a

Laplacian Pyramid, providing a texture image for

each of the corresponding models to be derived from

the range images. Starting from the apex, i.e the

lowest resolution image in the pyramid, each pixel

from the range image is transformed from range

space to World Coordinates. The colour for this

point is derived from the corresponding Texture

image pyramid. Once in World Coordinates, the

point goes through any pending viewing

transformations. Finally, the pixel is projected onto

the screen as a 3x3 Guassian kernel. This results in a

series of images, of varying sizes, depending upon

the level of the Pyramid they are generated from.

The images form an image pyramid, in screen-space,

with a Gaussian Image at the apex, followed by

Laplacian Images containing successively higher-

frequency detail.

Figure 2: Single-view Output Pyramid.

The resultant images can now be recombined to

form a Pyramid in viewport-space again. Though the

method outlined above renders a single view, it is

extendable to multiple views without any additional

effort. A multi-view image can be obtained by

repeating the process with another view (another

input range image and texture image), and projecting

each corresponding level into the same output space.

The resulting images represent an image pyramid as

before. The result of the reconstruction of this

pyramid, however, is a blending of the two views

together via a multi-resolution spline as proposed by

Burt and Adelson (1983b).

Figure 3: Multi-view Output Pyramid.

3.1 Details of the Rendering Algorithm

The proposed method makes extensive use of image

pyramids as defined by Burt (1983a) for seamless

splining of the two views, and of Gaussian kernels

for sub-pixel anti-aliased display of the points. An

explanation of the multi-resolution spline can be

found in (Burt and Adelson, 1983b). An explanation

of how the Gaussian kernel is used for rendering

follows.

3.2 The Gaussian Kernel

Figure 4: A continuous Gaussian function (left) and its

approximation by a 3x3 pixel kernel (right). Shifted

versions in x,y allow sub-pixel Gaussian splat placement.

A single point can be approximated by a continuous

Gaussian function. For display, it needs to be

transformed into discrete values. For every fractional

pixel value, a new Gaussian is generated, offset from

the centre. In order to speed up the process, a Look-

Up Table was generated for 10,000 kernels thereby

providing 0.01pixel shift resolution in x,y.

If the image is rendered using the Gaussian

kernels as-is, several bright patches appear on the

final image where the Gaussian kernels overlap. The

PYRAMIDAL MULTI-VIEW PBR - A Point-based Algorithm for Multi-view Multi-resolution Rendering of Large Data

Sets from Range Images

213

image is therefore normalized by dividing it by a

Splat map.

Figure 5: The Splat map combining the two overlapping

input range map views.

The Splat map is generated by first rendering

the Gaussian kernels without colour from the texture

map into a separate buffer to keep a count of the

contribution from each Gaussian kernels that falls

into each pixel. This defines each pixels weight. The

un-normalized image is then divided pixel-wise by

this Splat map to obtain the final, normalized, image.

4 ONGOING WORK

From the current results, it is obvious that Hidden-

Surface Removal is required. Hidden-surface

Removal may be implemented by treating a group of

three connected points as an implicit polygon, and

performing Back-Face Culling, and ordering the

points using any of the well-known polygon-

ordering techniques such as the Z-Buffer.

The existing method combines two views in

image space via a multi-resolution spline, however,

for the purposes of measurement, it is necessary to

employ a multi-view algorithm that merges the

underlying data. Ju et al (2004) describes view-

integration based on polygons. We propose to

extend their algorithm to work with range images

and image pyramids, and make improvements to the

basic algorithm in the process. The algorithm

proposed by Ju et al begins with a blue-screen stereo

capture of an object. The blue-screen permits

masking of the background, selectively isolating the

object. The range images are then decomposed into

subset patches, categorising elements into visible,

invisible, overlapping, and unprocessed patches

when compared with a second range image. To

resolve ambiguities in a range image, a confidence

competition is conducted, whereby overlapping

patches are culled, and the remaining winning

patches are merged into a single mesh. It should be

noted that this process needs to be carried out only

once, as a pre-processing step.

Since our data representation uses groups of

points (as opposed to polygons), it will work on

individual pixels rather than breaking down the

range image into patches. The following algorithm

summarizes the process:

Since multi-view stereo-photogrammetry relies

on range images being generated from cameras in

close vicinity, there will be considerable overlap

between various range images that are produced

from multiple views, especially those that are close.

Before we integrate the models, it is necessary to

take care of this redundant data. As proposed by Ju

et al, it is necessary to carry out a 'competition' in

which the best data from each range image is

selected.

First, it is necessary to find precisely the

redundant data, i.e., where range images overlap.

Hence, we traverse through each range image, and

scan every other range image from this point-of-

view (by projecting them into range image space) to

find the overlapping pixels.

= Num of Range Images

Masks of All range Images = 0

loop from 1 to N

Compare every Range image i

With every other Range Image j

if i != j

{

project range-map j onto i

find overlapping pixels

for each overlapping pixel

{

For both views j and j:

use confidence,

normal_map, chroma_map to

find competition_weight_i

and competition_weight_j

for current pixel

if comptetion_weight_i -

competition weight of j <

threshold:

mask[currentpixel] = 1.0

}

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

214

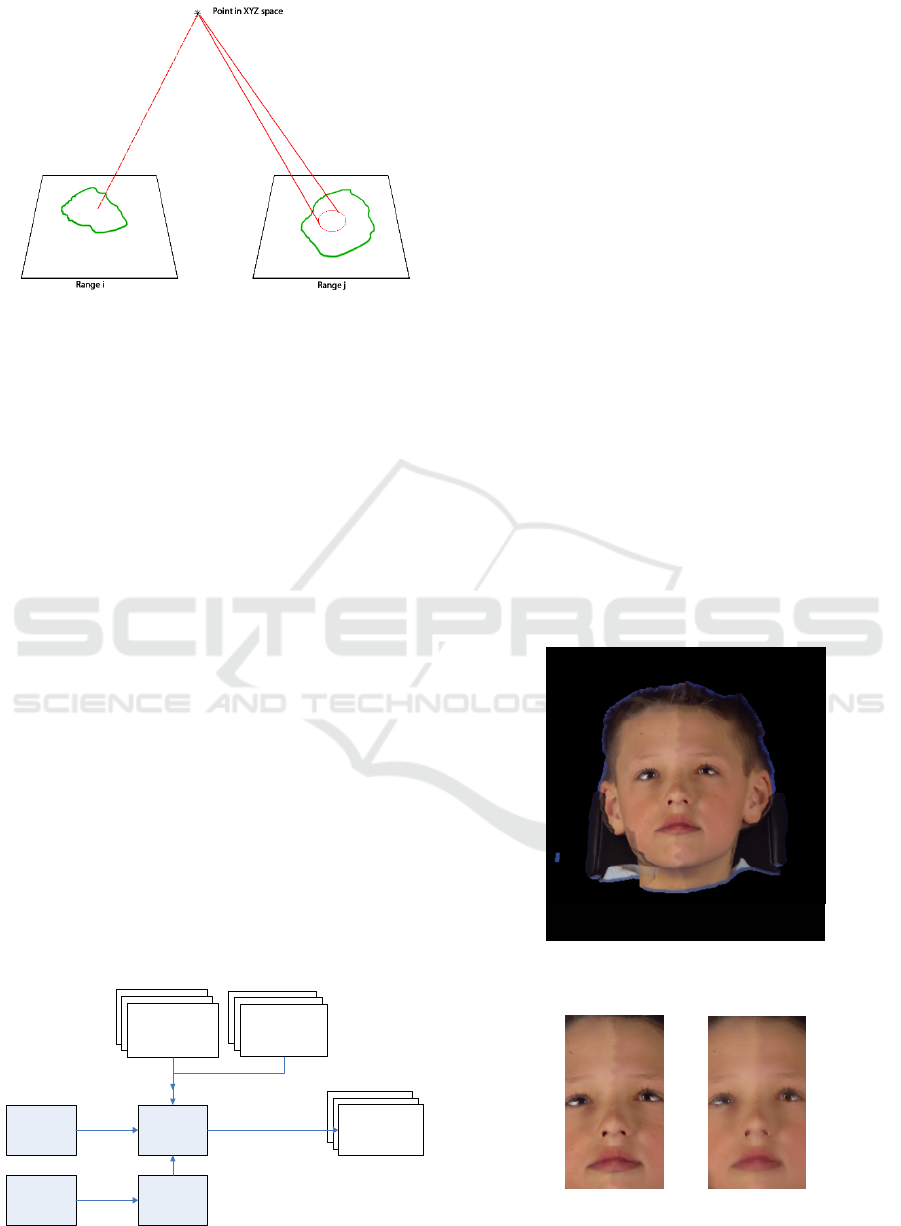
Figure 6: Scanning range image j from the point-of-view

of range image i.

For each overlapping pixel from both views

(view j and View i), we can isolate relevant data

from the background with the help of a blue-

screen/chroma mask we call S. If the pixel is

deemed to be part of the model (and not the

background), we can proceed to calculate the

confidence that a pixel is visible from this view with

the help of a “normal map” as well as a “confidence

map” of the same view, depicting how confident the

3D scanner was about the regeneration of each

individual point in 3D. We call the Confidence value

C. In addition, for both views, for every overlapping

pixel (in range space), we can consider how visible a

point is to a particular view by checking how closely

the normal points towards the view. We can

represent this as V (for Viewing-Angle). The three

maps together, then provide a selection mask with

values [0..1], with 1 being completely visible, 0

being completely invisible, and a value in-between

depicting a semi-visible pixel. This can be written

as:

Competition Weight = S C V (1)

The entire process is summarized in Figure 7 as

follows:

Range i

Range j

Overlapping Pixels

Range Image j

in Range-Image

space of i

Range Image I

New Mask

RANGE IMAGE J

Chroma Mask

Confidence

Map

Normals

RANGE IMAGE I

Chroma Mask

Confidence

Map

Normal s

Figure 7: Confidence Competition overview.

At this stage, we can determine which of the two

views won the competition for this particular pixel.

If it was view j, then we mask the current pixel in

view i to that during projection, we will not choose

this pixel from view i again.

A peculiar case arises when for a certain point,

two views tie in the competition, i.e, when there is a

'draw'. In such a case, there are several paths that can

be taken. An assortment of fusion/blending

techniques is available. Which one of these

techniques is most effective is a question that must

be further investigated.

Once data-integration has been accomplished,

measurement operations can be carried out natively

over the range images. Traversing over the range

images is decidedly straightforward due to the range

image’s matrix-like nature.

5 RESULTS AND CONCLUSIONS

Though the work is still ongoing, initial results of

our system can be seen in the images that follow. An

initial test result, based on a shallow blend, reveals

the sources of the two input views, Figure 8. By

creating a 6 layer deep pyramid, the blend better

conceals the join between views, Figure 9.

Figure 8: Result of the proposed method with a Pyramid 3

levels deep.

Figure 9: (Left) The result of the proposed method with a

Pyramid 3 levels deep (Right) The result with a pyramid 6

levels deep.

PYRAMIDAL MULTI-VIEW PBR - A Point-based Algorithm for Multi-view Multi-resolution Rendering of Large Data

Sets from Range Images

215

Without hidden point removal, self occluded

regions of the model blend together in areas such as

the chin and the ear towards the left of the image.

While, the rendering is currently not carried out in

real-time, the proposed method lends itself to GPU

optimization. The above issues will be addressed in

during our ongoing research work to implement the

complete system for clinical visualisation,

manipulation, measurement and analysis of multi-

view range images of surface anatomy.

REFERENCES

A. Hilton, A.J. Toddart, J. Illingworth, and T. Windeatt.

1996. Reliable surface reconstruction from multiple

range images. In Fourth European Conference on

Com- (a) (b) (e) (f) (g) (c) (d)

Burt, P. J. and Adelson, E. H., April 1983a. The Laplacian

Pyramid as a Compact Image Code, IEEE Trans. on

Communications, pp. 532--540.

Burt, P. J. and Adelson, E. H. 1983b. A multiresolution

spline with application to image mosaics. ACM Trans.

Graph. 2, 4 (Oct. 1983), 217-236.

Dimensional Imaging, www.DI3D.com (28 Oct 2008)

Gortler, S. J., Grzeszczuk, R., Szeliski, R., and Cohen, M.

F. 1996. The lumigraph. In Proceedings of the 23rd

Annual Conference on Computer Graphics and

interactive Techniques SIGGRAPH '96. ACM, New

York, NY, 43-54.

Hübner, T., Zhang, Y., and Pajarola, R. 2006. Multi-view

point splatting. In Proceedings of the 4th international

Conference on Computer Graphics and interactive

Techniques in Australasia and Southeast Asia (Kuala

Lumpur, Malaysia, November 29 - December 02,

2006). GRAPHITE '06. ACM, New York, 285-294.

Ju, X., Boyling, T., Siebert, J. P., McFarlane, N., Wu, J.,

and Tillett, R. 2004. Integration of range images in a

Multi-View Stereo System. In Proceedings of the

Pattern Recognition, 17th international Conference on

(Icpr'04) Volume 4 - Volume 04 (August 23 - 26,

2004). ICPR. IEEE Computer Society, Washington,

DC, 280-283.

Levoy, Whitted, January, 1985. Technical Report 85-022.

The Use of Points as a Display Primitive, Computer

Science Department, University of North Carolina at

Chapel Hill.

Lorenson, Cline, 1987. Marching Cubes: A High

Resolution 3D Surface Construction Algorithm. In

SIGGRAPH '87 Proc., vol. 21, pp. 163-169.

Marroquim, R., Kraus, M., and Cavalcanti, P. R. 2008.

Special Section: Point-Based Graphics: Efficient

image reconstruction for point-based and line-based

rendering. Comput. Graph. 32, 2 (Apr. 2008), 189-203.

Räsänen, J. 2002. Surface Splatting: Theory, Extensions

and Implementation. Master's thesis, Helsinki

University of Technology.

Rusinkiewicz, S. and Levoy, M. 2000. QSplat: a

multiresolution point rendering system for large

meshes. In Proceedings of the 27th Annual Conference

on Computer Graphics and interactive Techniques

International Conference on Computer Graphics and

Interactive Techniques. ACM Press/Addison-Wesley

Publishing Co., New York, NY, 343-352.

Siebert,J.P. Marshall,S.J. 2000. Human Body 3D imaging

by speckle texture projection photogrammetry Sensor

Review. Volume 20, No 3 pp 218-226.

Turk, Levoy, 1994. Zippered polygon meshes from range

images. In Proceedings of the 21st Annual Conference

on Computer Graphics and interactive Techniques

SIGGRAPH '94. ACM, New York, NY, 311-318.

Zwicker, M., Pfister., H., Baar, J. V., and Gross, M. 2001

Surface Splatting. In Computer Graphics, SIGGRAPH

2001 Proceedings, pages 371--378. Los Angeles, CA.

GRAPP 2009 - International Conference on Computer Graphics Theory and Applications

216