
CRAWLING DEEP WEB CONTENT THROUGH QUERY FORMS
Jun Liu, Zhaohui Wu, Lu Jiang, Qinghua Zheng and Xiao Liu
MOE KLINNS Lab and SKLMS Lab, Xi’an Jitaotong University, Xi'an 710049, China
Keywords: Deep Web, Deep Web Surfacing, Minimum Executable Pattern, Adaptive Query.
Abstract: This paper proposes the concept of Minimum Executable Pattern (MEP), and then presents a MEP
generation method and a MEP-based Deep Web adaptive query method. The query method extends query
interface from single textbox to MEP set, and generates local-optimal query by choosing a MEP and a
keyword vector of the MEP. Our method overcomes the problem of “data islands” to a certain extent which
results from deficiency of current methods. The experimental results on six real-world Deep Web sites show
that our method outperforms existing methods in terms of query capability and applicability.
1 INTRODUCTION
There is an enormous amount of information buried
in the Deep Web, and its quantity and quality are far
beyond the “surface web” that traditional search
engines can reach (Michael, 2001). However, such
information cannot be obtained through static html
pages but dynamic pages generated in response to a
query through a web form. Due to the enormous
volume of Deep Web information and the
heterogeneity among the query forms, effective
Deep Web crawling is a complex and difficult issue.
Deep web crawling aims to harvest data records
as many as possible at an affordable cost (Barbosa,
2004), whose key problem is how to generate proper
queries. Presently, a series of researches on Deep
Web query has been carried out, and two types of
query methods, namely prior knowledge-based
methods and non-prior knowledge methods, have
been proposed.
The prior knowledge-based query methods need
to construct the knowledge base beforehand, and
generate queries under the guidance of prior
knowledge. In (Raghavan, 2001) proposed a task-
specific Deep Web crawler and a corresponding
query method based on Label Value Set (LVS)
table; the LVS table as prior knowledge is used for
passing values to query forms. (Alvarez, 2007)
brought forward a query method based on domain
definitions which increased the accuracy rate of
filling out query forms. Such methods automate
deep crawling to a great extent (Barbosa,2005),
however, have two deficiencies. First, these methods
can only perform well when there is sufficient prior
knowledge, while for the query forms that have few
control elements (such as a single text box), they
may have an unsatisfactory performance. Second,
each query is submitted by filling out a whole form,
which reduces the efficiency of Deep Web crawling.
The non-prior knowledge methods are able to
overcome the above deficiencies. These methods
generate new candidate query keywords by
analyzing the data records returned from the
previous query, and the query process does not rely
on prior knowledge. Barbosa et al. first introduced
the ideas, and presented a query selection method
which generated the next query using the most
frequent keywords in the previous records (Barbosa,
2004). However, queries with the most frequent
keywords in hand do not ensure that more new
records are returned from the Deep Web database.
(Ntoulas, 2005) proposed a greedy query selection
method based on the expected harvest rate. In the
method, candidate query keywords are generated
from the obtained records, and then their harvest
rates are calculated; the one with the maximum
expected harvest rate will be selected for the next
query. (Wu P, 2006) modeled each web database as
a distinct attribute-value graph, and under this
theoretical framework, the problem of finding an
optimal query selection was transferred into finding
a Weighted Minimum Dominating Set in the
corresponding attributed-value graph; according to
the idea, a greedy link-based query selection method
was proposed to approximate the optimal solution.
634
Liu J., Wu Z., Jiang L., Zheng Q. and Liu X.
CRAWLING DEEP WEB CONTENT THROUGH QUERY FORMS.
DOI: 10.5220/0001830806290637
In Proceedings of the Fifth International Conference on Web Information Systems and Technologies (WEBIST 2009), page
ISBN: 978-989-8111-81-4
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Compared with the prior knowledge-based methods,
the non-prior knowledge methods improve the query
capability on Deep Web crawling. However, these
methods suffer from the following three limitations:
first, queries are only based on single text box and
the candidate keywords are assumed to be suited to
the text box; second, query selection decision is
made solely based on the obtained records, namely
“myopia estimation problem” (Wu P, 2006); third,
query selection lacks sufficient knowledge in the
initial period. The three problems limit the query
capability on Deep Web crawling, and result in the
phenomenon called “data islands” which means the
total acquired records may constitute only a small
fraction of the target database.
In this paper, we propose the concept of
Minimum Executable Pattern (MEP) and a MEP-
based Deep Web adaptive query method. The query
method extends query interface from single textbox
to MEP set; it performs a query by choosing a MEP
and a keyword vector of the MEP, and generates the
next query with the maximum expected efficiency
adaptively through the acquired information. This
method not only has the advantages over the non-
prior knowledge methods, but also has the ability to
solve the problem of “data islands” by making the
most of query capability of elements in MEP set.
The experimental results on six real-world Deep
Web sites show that our method outperforms
existing methods in terms of query capability and
applicability.
The rest of the paper is organized as follows:
Section 2 introduces the concept of MEP. Section 3
describes the algorithm for generating the MEP set
of a given query form. Section 4, the core of this
paper, studies the MEP-based adaptive query
method and the convergence of the related
algorithm. The experimental results are discussed in
Section 5, and conclusions and future work are
offered in the final section.
2 FUNDAMENTAL CONCEPTS
Definition 1: Query Form. A query form F is a
query interface of Deep Web, which can be defined
as a set of all elements in it.
1
{ ,..., }
n
Fe e= , where
i
e is an element of F, such as a checkbox, text box or
radio button.
Each element
i
e of F has its domain
i
D which is
the set of values associated with
i
e . If
i
D is a finite
set, then
i
e is a finite domain element, else
i
e is an
infinite domain element. Elements are usually
associated with some descriptive text to help users
understand the semantics of the element, namely
labels. The expression
()
i
label e is used to denote the
label of
i
e ( Raghavan, 2001).
Definition 2: Executable Pattern (EP). Given a
query form
1
{ ,..., }
n
Fe e= ,
1
{ ,..., } 2
F
m
ee
′′
∀∈,1≤m≤n,
1
{ ,..., }
m
ee
′
′
is an executable pattern of F if the Deep
Web database returns the corresponding results after
the query with value assignments of elements in
1
{ ,..., }
m
ee
′
′
is issued.
Executable Pattern satisfies the following
monotonicity properties:
1. If
1
{ ,..., }
m
ee
′
′
is an executable pattern, then any
subset of F that contains
1
{ ,..., }
m
ee
′′
is also an
executable pattern.
2. If
1
{ ,..., }
m
ee
′
′
is not an executable pattern, then
any subset of
1
{ ,..., }
m
ee
′
′
is not an executable
pattern.
The result records returned based on an
executable pattern may also be null. A query based
on a non-executable pattern can not perform a
successful database search, and usually leads to an
error report or switches to another page.
Definition 3: Minimum Executable Pattern
(MEP). If
1
{ ,..., }
m
ee
′
′
is an executable pattern of
query form
1
{ ,..., }
n
F
ee= (1≤m≤n), then
1
{ ,..., }
m
ee
′
′
is a MEP iff any proper subset of
1
{ ,..., }
m
ee
′
′
is not an executable pattern. We may
rewrite it as
1
( , ..., )
m
M
EP e e
′
′
.
The keyword vector
1
( ,..., )
m
kv kv kv= makes a
value assignment for
1
( , ..., )
m
M
EP e e
′′
, where
ii
kv D∈
′
, i=1,2,…,m. If there is an infinite set
i
D
′
,
then the MEP is called infinite domain MEP, or
IMEP for short; while if each
i
D
′
is a finite set, then
the MEP is called finite domain MEP (FMEP). All
MEP of the query form F constitute the MEP set of
F which is denoted as S
MEP
.
According to the monotonicity properties of EP,
we can draw the following inference:
Inference 1: An executable pattern
1
{ ,..., }
m
ee
′′
is a
MEP iff all its subsets of size m-1 are not EP.
Deep web crawling aims to retrieve data records
from a web database through iterative queries on a
given query form F. In this process, the MEP set
CRAWLING DEEP WEB CONTENT THROUGH QUERY FORMS
635

S
MEP
of the query form F is generated firstly and
then all subsequent queries are performed based on
the MEP set. For this reason, our study focuses on
such two critical issues: first, how to generate the
MEP set of a given query form; second, how to
select a proper MEP and its keywords vector to
harvest data records from web database efficiently.
3 MEP SET GENERATION
A naive method to generate the MEP set is to
enumerate all combinations of elements in the form
F. If the size of F is n, then the number of
combinations to be checked totals is about 2
n
. For
this reason, the efficiency of enumeration will
sharply drop when n grows large.
Elements in a form are not independent but
always have connection with each other, such as
“start city” and “destination city” in a ticket query
form. Such elements always appear simultaneously
in the same MEP, and their combination is called
“Condition Pattern” (CP for short) (Zhang Z, 2004).
By using CP, the MEP set can be generated with
greater granularity than element, which greatly
improves the efficiency of MEP set generation.
There have existed several methods of generating
all CPs of a query form (He B, 2006) (Zhang Z,
2004). For example, Zhang Z. et al. proposed the 2P
grammar & best-effort parser model, by using
which, a query form can be parsed into a complete
parser tree (Zhang Z, 2004), and the CP nodes in this
tree are corresponding with the CPs of the form. The
CP set can be easily generated through finding all
the CP nodes in this tree.
Let the CP set be S
CP
, and the initial MEP set
S
MEP
is empty. The algorithm MEPGeneration(S
CP
,
S
MEP
) will generate the MEP set S
MEP
based on the
CP set S
CP
. In order to facilitate the description of
the algorithm, we introduce a function
μ
defined as:
{}{}
()= -A
A
xx A
μ
∈ ( A ≠∅). The algorithm is shown
in Fig.1.
Figure 1: Algorithm for generating the set of MEP.
According to the monotonicity properties of EP,
the algorithm uses divide-and-conquer to generate
S
MEP
in a recursive way. Considering that a single
CP is also a MEP in most cases, we can move all
CPs that are EPs from SCP to SMEP before
executing the above algorithm, which can accelerate
the generation of MEP set.
4 QUERY BASED ON MEP
Once the MEP set S
MEP
of a given form is obtained,
the next task is to select suitable MEPs and the
corresponding keywords vectors to perform iterative
queries on the target Deep Web database. In this
section, we formulate the problem of MEP-based
query, and on the basis of that, propose a MEP-
based adaptive query algorithm as well as the
estimation methods of two key parameters. Finally,
we give the convergence analysis of our query
algorithm.
4.1 Formal Description of MEP-based
Query
Let q
i
(kv, mep
j
) be the i
th
query on the target Deep
Web site, and q
i
(kv, mep
j
) is implemented using the
MEP mep
j
and its corresponding keyword vector kv.
Here, mep
j
∈S
MEP
includes m elements and kv=(kv
1
,
kv
2
, …, kv
m
) is a m-dimensional vector accordingly.
q
i
(kv, mep
j
)
can be abbreviated as q
i
.
Given a query q
i
, P (q
i
) is used to denote the
fraction of data records returned form the web
database through the query q
i
. P(q
1
∧ … ∧ q
i
)
represents the fraction of the common records that
are returned from q
1
, q
2
,... and q
i
. Similarly, we use
P(q
1
∨…∨q
i
) to represent the fraction of the unique
records that are returned from q
1
or q
2
,....or q
i
.
Additionally, P
new
(q
i
) stands for the fraction of the
new records that have not been retrieved from
previous queries from q
i
. P
new
(q
i
)
is computed from
Equation(1):
P
new
(q
i
) =P(q
1
∨.. q
i
) - P(q
1
∨.. q
i-1
)
(1)
In order to measure the resource consumption of
issued query, we introduce cost(q
i
) to represent cost
of issuing the query q
i
. Depending on the scenario,
the cost can be measured either in time, network
bandwidth, or the number of interactions with the
site. In this study, we measure cost in terms of
consumed time, as follows:
cost(q
i
(kv,mep
j
))=
t
q
(mep
j
)+t
r
P(q
i
(kv,mep
j
))+t
d
P
new
(q
i
(kv,mep
j
))
(2)
MEPGeneration (S
CP
, S
MEP
)
Step 1: If none of
cp
()S
μ
is EP
Add S
CP
to S
MEP
;
Return;
Step 2: Else for each
cp cp
()SS
μ
′
∈
that is EP
MEPGeneration (
cp
S
′
, S
MEP
);
Step 3: Return S
MEP
.
WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies
636

In the above equation, query cost consists of
three factors, t
q
(mep
j
) is fixed part of the query cost,
which includes the query transmitting time and
query processing time by Deep Web database; t
r
is
proportional to the average time of handling a result
record; while t
d
is proportional to the average time of
downloading a new result record.
With the above notations, we can formalize
MEP-based query on Deep Web as follows: under
the constraint
1
()
i
n
i
cost q T
=
≤
∑
, find a sequence of
queries q
1
,…q
n
that maximize P
new
(q
1
∨ … ∨ q
n
).
Here, T is the maximum cost constraint.
4.2 Adaptive Query Algorithm
The sequence of queries q
1
,…q
n
that maximize
P
new
(q
1
∨…∨q
n
) is called global-optimal query set.
Even if all results of candidate queries are clearly
known, finding the global-optimal query set is an
NP-Hard problem. An efficient algorithm to solve
this problem in polynomial time has yet to be found.
For this reason, we present an adaptive query
algorithm based on MEP that aims at finding a local-
optimal query set to approximate the global optimal
query set. A query is the local-optimal if it has the
maximum value of Efficiency. Efficiency is defined
as follows:
Definition 4: Efficiency. Efficiency(q
i
) is used to
quantify new queries returned from q
i
per unit cost:
Efficiency(q
i
(kv,mep))=P
new
(q
i
(kv,mep))/cost(q
i
(kv,mep)) (3)
By observing equation (2) and (3), it can be seen
that to compute Efficient(q
i
) is actually to compute
P
new
(q
i
). Using chain rules, P
new
(q
i
) can be rewritten
as:
P
new
(q
i
(kv,mep
j
))=P
new
(q(mep
j
)) P
new
(q
i
(kv|mep
j
)) (4)
In equation (4), the value of P
new
(q
i
) is
determined by a joint decision of both P
new
(q(mep
j
))
and P
new
(q
i
(kv | mep
j
)). P
new
(q(mep
j
)) is also called
harvest rate of the mep
j
(i.e. the capability of
obtaining new records), which is independent of
choice of keyword vectors, but depends on the
pattern mep
j
itself. For example, assuming that a
Deep Web site about academic paper has MEP set
S
MEP
= {mep(Keywords),mep(Abstract)}, it is
obvious that the harvest rate of “Abstract” pattern is
greater than that of “Keywords”, since keywords are
usually included in abstract. P
new
(q
i
(kv|mep
j
))
represents the conditional harvest rate of kv among
all candidate keyword vectors of given mep
j
. The
value depends on the capability of obtaining new
records of selected keyword vector.
The estimation of P
new
(q(mep
j
)) and P
new
(q
i
(kv |
mep
j
)) is the key to find the local-optimal query in
our adaptive query algorithm. The process of
estimation is based on currently available records. In
the early stage of Deep Web crawling, as feedback
records are relatively scarce, the selection of
keyword vectors is lack of basis and inevitably leads
to the problem of “data islands”. To address the
problem, we introduce an LVS table in our
algorithm. The algorithm is divided into two phases.
When the number of queries is less than a certain
threshold s, i.e. in the data accumulation phase, the
algorithm uses Probabilistic Ranking Function
(Raghavan, 2001), an LVS value assignment
method, to select the most promising kv and obtains
data from the target Deep Web database. Once the
number of queries is greater than or equal to s, the
algorithm switches to the prediction phase; in this
phase, it analyzes currently available data and
estimates the most promising query. The algorithm
finally outputs the next local-optimal query. The
algorithm flow is shown in Fig.2.
In the following, the methods for computing
P
new
(q(mep
j
)) and P
new
(q
i
(kv | mep
j
))are discussed in
details.
4.2.1 Prediction for P
new
(q(mep
j
))
In practice, we use P
new
(q
i
(mep
j
)) to denote the
predicted value of P
new
(q
i
(mep
j
)) at the i
th
query ,and
introduce two methods to accomplish the task.
Figure 2: Adaptive query algorithm based on MEP.
1) Continuous prediction: the current harvest
rate of a MEP totally depends on the harvest rate of
the latest issued query by the MEP, namely:
CRAWLING DEEP WEB CONTENT THROUGH QUERY FORMS
637

1
i-1 j
1
1
i-1 j
((, ))
q use mep
((, ))
(( ))
(( ))
q not use mep
−
−
−
⎧
⎪
×
⎪
=
⎨
⎪
⎪
⎩
new i j
ij
new i j
new i j
Pqkvmep
ZPq kvmep
Pqmep
Pqmep
Z
(5)
where Z is a normalization factor. Assume q
i-1
uses mep
j
, then
1
1
1
((, ))
(( ))
((, ))
new i j
new i t
ij
tj
Pqkvmep
ZPqmep
Pq kvmep
−
−
−
≠
=+
∑
.
Continuous prediction method performs well on
FMEP since there is no significant variation in
harvest rates among different keyword vectors in
most cases, while it may not be effective for IMEP.
2) Weighted prediction: the current harvest rate
of a MEP depends on all its previous harvest rates of
issued query by the MEP, namely:
1
1
1
-1
1
-1
((, ))
(( ))(1)
((, ))
use
(( ))
(( ))
not use
new i j
new i j
ij
ij
new i j
new i j
ij
Pqkvmep
vP q mep v
Pq kvmep
qmep
Pqmep
Z
Pqmep
qmep
Z
−
−
−
−
⎧
+−
⎪
⎪
⎪
=
⎨
⎪
⎪
⎪
⎩
(6)
where v is a weight to measure the dependence of
the current harvest rate on the past experience.
Experiments show that v ranges from 0.6 to 0.8. Z is
a normalization factor; assume that q
i-1
use mep
j
,
then,
1
11
1
((, ))
( ( )) ( ( )) (1 )(
((, ))
new i j
new i t new i j
tj
ij
Pqkvmep
Z P q mep vP q mep v
Pq kvmep
−
−−
≠
−
=++−
∑
Weighted prediction method is the generalized form
of continues prediction method, and works well on
both FMEP and IMEP. Furthermore, the method is
not sensitive to the initial value of each pattern in
equation (6). So we adopt the weighted prediction
method in our algorithm to predict P
new
(q(mep
j
)).
4.2.2 Estimation for P
new
(q
i
(kv|mep
j
))
The aim of estimating the P
new
(q
i
(kv|mep
j
)) is to
identify the most promising keyword vector of the
given mep
j
. According to equation (1), we have
P
new
(q
i
(kv|mep
j
))
=P(q
i
(kv|mep
j
))-P(q
i
(kv|mep
j
)
∧
(q
1
∨
…
∨
q
i-1
))
(7)
In equation (7), P(q
i
(kv|mep
j
)) represents the
conditional capacity of obtaining data records of kv
among all candidate keyword vectors of mep
j
.
P(q
i
(kv|mep
j
)∧(q
1
∨…∨q
i-1
)) represents the fraction
of previously downloaded unique records which
contain kv of mep
j
. The value of P(q
i
(kv|mep
j
)∧ (q
1
∨ … ∨ q
i-1
)) can be calculated through currently
available data, whereas P(q
i
(kv|mep
j
)) needs to be
estimated. The following part focuses on the
calculation of these two values.
In order to calculate P(q
i
(kv|mep
j
)∧(q
1
∨…∨q
i-
1
)), we introduce the notion of SampleDF(w) ,which
means the document frequency of observed word w
in sample croups {d
1
,...,d
s
} (Ipeirotis, 2002).
SampleDF(w) =
1
s
k
k
b
=
∑
, b
k
=1 if w in d
k
, 0 otherwise.
Unfortunately,
SampleDF(w) cannot be applied to
our work, for it only focuses on single keyword and
ignores the compatibility between
kv and mep
j
. To
identify the contribution of the document frequency
of
m-dimensional keyword vector on a given
particular pattern, we introduce cos<kvx
k
,mepx>,
where
kvx
k
is the corresponding Boolean vector of
kvx in d
k
, and similarly mepx is the Boolean vector
of
mep. Assume that cosine value of null vector and
any vector is 0. Here, we define the document
frequency of
kv on a given mep in sample croups
{d
1
,...,d
s
} as SampleDF(kv|mep), which is calculated
as follows:
11
cos ( )(| )
k
k
k
ss
kk
kvx mepx
kvx mepx
kvx ,mepxSampleDF kv mep
==
==
∑∑
i
(8)
In equation (8), mepx = (mepx
1
,..., mepx
m-1
,
mepx
m
). Unlike IMEP, FMEP keyword vector can be
obtained by parsing the form
F. In order to eliminate
the influence on predicting keyword vector of IMEP,
we assign zero to
mepx
i
of finite element; kvx
k
=
(kvx
k
1
,...kvx
k
n
), for given kvx and mep, the kvx
k
generation algorithm is shown in fig.3, where
label(
kv
i
) is the keyword label in d
k
, label(e
i
) is the
label of the
i
th
element of the mep.
The reason of label(kv
i
) = null in Step 4 is that
either the label of
kv
i
is absent or the label can’t be
extracted. To solve this problem, the algorithm
borrows the idea from (Raghavan, 2001) to find the
most relevant label of the missing label. In Step 6,
M
v
(x) is the fuzzy value of x in LVS. According to
fig.3, the
SampleDF(kv|mep) of a given FMEP is 0.
Figure 3: Algorithm for generating the vector kvx
k
.
Step 1: i = 0;
Step 2: i++; If i > dimension of mep then return kvx
k
;
Step 3: If mepx
i
= 0 then kvx
k
i
= 0; Goto Step 2;
Step 4: If label(kv
i
) = null in d
k;
; Goto Step 6;
Step 5: If label(kv
i
) = label(e
i
) then kvx
k
i
= 1; Goto Step
2;Else then kvx
k
i
= 0; Goto Step 2;
Step 6: S
max
=0;
//Calculate the most relevant label in LVS
For each (L,V) entry in LVS
S = M
v
(kv
i
); If(S > S
max
) label(kv
i
)= L;
Step 7: Goto Step 5;
WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies
638

Obviously, when the given
mep is FMEP, all
candidate keyword vectors of mep can be obtained
by parsing the form
F. Assume that each pattern is
capable to obtain all records from the target Deep
Web database within limited time of queries, we can
simply use average value to estimate
P(q
i
(kv|mep
j
)):
P(q
i
(kv|mep
j
)) =
1
1
||
n
t
tD
=
∏
(9)
where
i
D is the domain of element
i
e in mep
j
.
Furthermore, suppose the
mep consists of p radio
buttons (or combo boxes)
e
1
,...e
t
,…e
p
, and q
checkboxes
e
p+1
,...e
p+t
,…e
p+q
, e
t
has m
t
buttons (|D
t
|
=
m
t
) and e
p+t
has r boxes (|D
p+t
| = 2
r
). Since the
domain size of a checkbox is an exponential
function of the number of its check buttons, it is
difficult to cover the full domain within acceptable
time. In order to improve efficiency of queries with
checkboxes, we replace the domain of a checkbox to
its subset with size of
h
t
(2≤h
t
≤r+2). Experimental
results indicate that the subset formed by empty set,
full set and sets of an individual checkbox can obtain
about 90% of total records in most cases. Based on
the above considerations, the value of
P(q
i
(kv|mep
j
))
can be further optimized as:
P(q
i
(kv|mep
j
)) =
1
1
pq p
t
t
tp t
hm
+
==
∏
∏
(10)
When the given mep
j
is IMEP and consists of p
radio buttons and q checkboxes, the value of
P(q
i
(kv|mep
j
)) is
P(q
i
(kv|mep
j
)) =
1
pq p
t
t
tp t
f
hm
+
==
∏
∏
(11)
Compared with equation (10), equation (11) is
more general. When the given
mep
j
is FMEP, f = 1,
which means that the query scope is the entire
database; when the given
mep
j
is IMEP, f is the
fraction of records including keywords of infinite
domain element on the given
mep
j
. Here, we exploit
Zipf-Mandelbrot law to estimate the fraction.
Alternative method such as Poisson Estimator
(Kenneth, 1995) may also be exploited. Zipf was the
first to observe that the word-frequency distribution
followed a power law, which was later refined by
Mandelbrot. Mandelbrot observed a relationship
between the rank
r and the frequency f of a word in a
text database (Mandelbrot, 1988):
f = ()r
γ
α
β
−
+ , where
α
,
β
and
γ
are parameters.
(12)
By analyzing dozens of experimental results, we
find kv also follows Zipf-Mandelbrot law. If the rank
value of
SampleDF(kv|mep) is known, the value of f
can also be estimated using equation (12). Then
equation (11) can be rewritten as follows:
P(q
i
(kv|mep
j
)) =
1
()
pq p
t
t
tp t
r
hm
γ
αβ
−
+
==
+
∏
∏
.
(13)
Once SampleDF(kv|mep) and P(q
i
(kv|mep
j
)) are
calculated, P
new
(q
i
(kv|mep
j
)) can be predicted as
follows: a candidate query is formulated as a 4-tuple
(
MEP, Keyword Vector, SampleDF, ActualDF),
where
ActualDF indicates the actual number of
records returned by the issued query; all the 4-tuples
of candidate queries construct the query candidate
pool. Our predicting algorithm manages the query
candidate pool based on the acquired data records of
the last query, sorts all 4-tuples in the pool according
to
sampledf, and then fits equation (12) with the rank
and actualdf /S (the size of the target database)of all
tuples that meet
sampledf*actualdf≠0. Subseque-
ntly,
P
new
(q
i
(kv|mep
j
)) of all the tuples which meet
actualdf =0 can be calculated according to equation
(11). The detailed algorithm is shown in Fig.4.
Figure 4: Algorithm for predicting P
new
(q
i
(kv| mep
j
)).
Step 1: Create a Tuple Set(Keyword Vector, MEP,
SampleDF, ActualDF);
Step 2: Fetch a new downloaded document d
k
; If no more
document then Goto Step 7;
Step 3: If d
k
is not a new document Goto Step 2;
Step 4: Find out all (Keyword Vector, MEP) pair (kv,mep)
and its corresponding sampledf in d
k
;
Step 5: For each (kv,mep)
If (kv,mep) pair exists in Tuple Set Then add
sampledf to SampleDF of that tuple;
Else Then add a new tuple
(kv,mep,sampledf,0) ;
Step 6: Goto Step 2;
Step 7: Sort all 4-tuples in descending order of SampleDF;
Step 8: For each tuple where sampledf * actualdf
≠ 0
Simulate
α
、
β
、
γ
in
()r
γ
α
β
−
+
using
tuple
rank and actualdf /S;
Step 9: For each tuple where ActualDF = 0
If(mep
j
is a FMEP) then f = 1;
Else then f =
()r
γ
α
β
−
+ ;
P
new
(q
i
(kv| mep
j
)) =
pq p
f
+
- sampledf / S;
CRAWLING DEEP WEB CONTENT THROUGH QUERY FORMS
639
4.3 Convergence Analysis
When to stop querying the web database is a
difficult issue, especially when the size of target
database is unknown. To make a decision on “When
to stop” requires the knowledge of the relationship
between fraction of new records and query cost.
Assume that the size of Deep Web database is
S, m
k
is the fraction of records returned by the i
th
query
and
a
k
is the cumulated fraction of new records
returned by previous i queries. We have a
k+1
= a
k
+
m
k *
p
k
, where p
k
is the fraction of new records in m
k
.
To simplify the calculation, we suppose that m
k
is
fixed and
p
k
can be approximated as /
k
SaS
−
,
where
k
Sa− is the number of records that are not
retrieved.
a
k+1
= a
k
+ m
k *
p
k
can be rewritten as
1
(/)
kk k
aamSaS
+
=+⋅− , from which equation
1
/1(1/)
k
k
aS mS
−
=− − is derived.
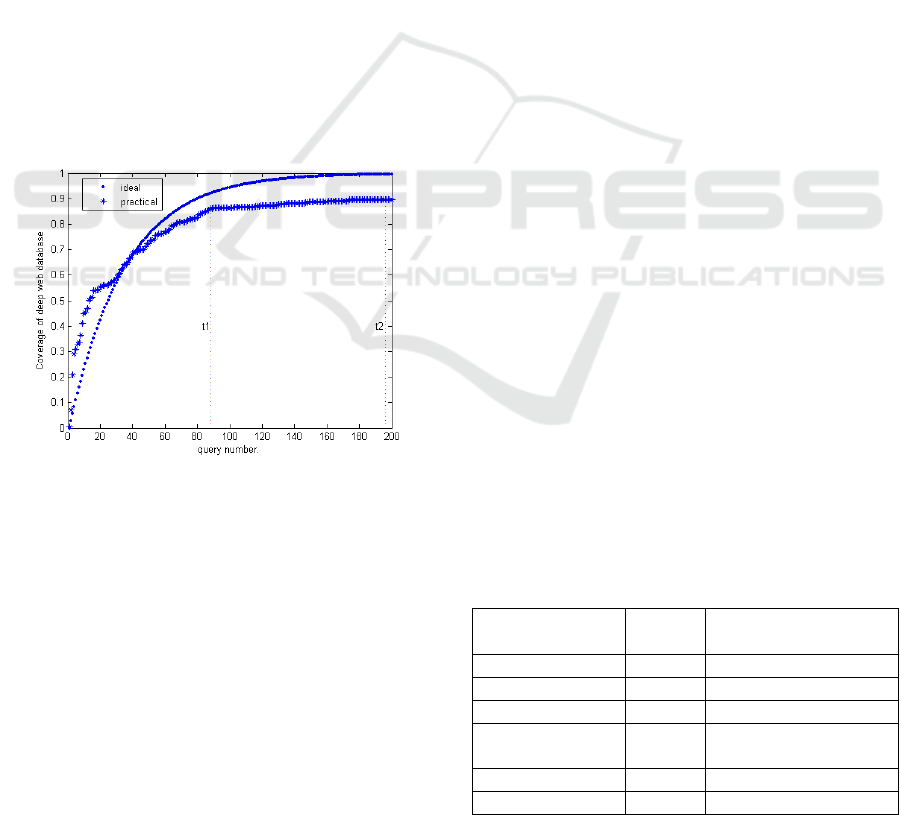
The comparison between ideal and practical
crawling fraction curve is carried out on dozens of
Deep Web databases. Take the Babe Raccoon
(http://vod.xjtu.edu.cn) as an example (see Fig.5).
On the y-axis, the database coverage is plotted,
while the x-axis represents the query number.
Figure 5: Comparison between ideal and practical craw-
ling fraction.
From both ideal and practical fraction curve, we
can find that when the fraction of the total records
obtained is approaching 90%, the harvest rate of the
subsequent queries is relatively
small and even
equals to 0 in a period of time. We call the
phenomenon “Crawler Bottleneck”. Deep web
crawling is a time-consuming task requiring a
significant amount of network resources. It would be
a waste of both time and network bandwidth if the
crawler doesn’t stop crawling when it comes into
“Crawler Bottleneck” phase. For example, stopping
crawling at
t
1
saves approximately 50% cost
compared to stopping at t
2
.
Assume
W is an obtained data window with the
size of ws, for a query q
i
, if i<ws,
(
)
1ii
Wq...q=∨∨
,if i≥ws,
()
1iiws i
Wq ...q
−+
=∨∨
,
cost
max
is the maximum available resource that a
crawler has, and
ε
is a very small positive number,
we present an strategy for stopping crawling: after
submitting
q
t
, if
1
()
t
imax
i
t
cost q cost W
ε
=
<>∧
∑
is
false, then stop crawling at
q
t
.
The value of
ws depends on cost
max
. The greater
the value of cost
max
, the bigger ws can reach. When
ws is determined,
ε
becomes the critical factor in the
strategy for stopping crawling. If
ε
is too small, the
stopping time will be prolonged, while more data
records may be obtained. To the contrary, the
crawler will stop at an earlier time and reduce
quantity of records retrieved. Therefore, the value of
ε
depends on the importance of the resource cost
and the crawling data.
5 EXPERIMENTS
To evaluate the performance of our MEP-based
adaptive query method, we performed experiments
on 6 real Deep Web sites and compared our method
with the representative methods of both non-prior
knowledge and prior knowledge-based methods, i.e.
adaptive query method based on single IDE (Infinite
Domain Element) (Ntoulas, 2005) and classical LVS
method (Raghavan, 2001).
5.1 Effectiveness of MEP-based
Adaptive Query
We test our MEP adaptive query method on 6 real
Deep Web sites, and the detailed experimental
results are shown in Table 1. Results show that our
method is quite effective for crawling Deep Web.
Table 1: Web sites and their experimental results.
URL(http) Domain Size/Harvest/query NO.
www.jos.org.cn Paper 1380/1380/143
cjc.ict.ac.cn Paper 2523/2523/13
www.jdxb.cn Paper 424/424/16
www.paperopen.co
m
Paper 743,444/730,000/39
9
vod.xjtu.edu.cn Movie 700/679/311
music.xjtu.edu.cn Music 154,000/146,967/386
WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies
640

5.2 Performance Comparison
We compare the crawling performance of our MEP-
based adaptive query (MEP or MEP adaptive for
short) method with the adaptive query method in
(Ntoulas, 2005). The experimental result is shown in
Fig. 6, where the x-axis represents the query
numbers and y-axis plots the database coverage.
We find that if the query form contains a FMEP,
our method shows distinct advantage over the
adaptive query method based on single IDE (see
Table 1). In order to evaluate performance of our
method on query forms only containing IMEPs, we
conduct other two experiments on Babe Raccoon
and Blue Lotus. Fig. 6(a) shows the experimental
results on Babe Raccoon, in which IDE1, IDE2,
IDE3 represent the crawling curve of the method in
(Ntoulas, 2005) on elements “movie name”, “actor”,
“director” respectively and MEP denotes the curve
of our method on three IMEPs. The experimental
results on Blue Lotus are plotted in Fig. 6(b), in
which IDE1, IDE2, IDE3 represent the crawling
curve of the method in (Ntoulas, 2005) on element
“author”, “publisher”, “title” respectively and MEP
denotes the curve of our method on these IMEPs.
Fig. 6(a) and 6(b) indicate that our method is more
efficient than the adaptive query method in (Ntoulas,
2005) on query forms only containing IMEPs.
The MEP adaptive method is based on multi-
pattern, and usually there are several MEPs to be
selected for each query. If each query takes the same
MEP, the method degenerates into single IDE-based.
From this point of view, the adaptive query method
based on single infinite element in (Ntoulas, 2005)
can be regarded as a special case of the MEP-based
adaptive method. Single pattern always brings
locality of the candidate keywords, while multi-
pattern can make full use of each pattern’s query
capacity, and break through the locality of the
keywords selection which leads to the problem of
“data islands”.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1 18 35 52 69 86 103 120 137 154 171 188 205 222 239 256 273 290
query number
coverage of deep web database
MEP
IDE1
IDE2
IDE3
Figure 6(a): Experiment on Baby Raccoon.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1 26 51 76 101 126 151 176 201 226 251 276 301 326 351 376
query number
coverage of deep web database
MEP
IDE1
IDE2
IDE3
Figure 6(b): Experiment on Paper Open.
In order to compare the crawling performance
between the MEP adaptive method and the prior
knowledge-based methods, we conduct experiments
on the site of Blue Lotus. In addition, we find that
the keyword with high value of
P(q
i
) in our method
is useful for the LVS method. If we update such
keyword’s
Mv value with its corresponding P(q
i
) in
the LVS table and then perform the LVS method
(Raghavan, 2001), it can remarkably improve
crawling efficiency. We call it the enhanced LVS
method. Fig. 7 shows the experimental results.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1 9 17 25 33 41 49 57 65 73 81 89 97 105 113 121 129
query number
coverage of deep web database
MEP Adptive
Enhanced LVS
Classical LVS
Figure 7: Comparison to Classical LVS.
According to Fig. 7, we can gain the efficiency
order of the three methods: the MEP adaptive
method > enhanced LVS method > classical LVS
method. Since the enhanced LVS method uses the
updated LVS table which improves the veracity of
the prior knowledge in LVS table, it contributes to
better crawling efficiency. However, because of the
inherent deficiencies of the prior knowledge-based
methods, it is still less efficient than the MEP
adaptive method.
CRAWLING DEEP WEB CONTENT THROUGH QUERY FORMS
641

6 CONCLUSIONS
Due to the heterogeneity among the query forms,
effective Deep Web crawling is a difficult issue. In
this paper, we propose the concept of MEP and a
MEP-based Deep Web adaptive query method. The
proposed method, like the prior knowledge-based
methods, has the ability to handle a variety of web
forms. Moreover, the method has an advantage of
good crawling efficiency over the non-prior
knowledge methods, and can overcome the problem
of “data islands” to a certain extent. Performance
comparisons with the related method validate the
better query capability of our method.
Although our method can be effective for most
Deep Web sites, it has the following limitations:
first, it may not perform well for some Deep Web
sites that limit the size of the result set; second, it
cannot support Boolean logic operators (e.g. AND,
OR, NOT) in queries. We will focus on these issues
in our future work.
ACKNOWLEDGEMENTS
The research was supported by the National High-
Tech R&D Program of China under Grant
No.2008AA01Z131, the National Science
Foundation of China under Grant Nos.60825202,
60803079, 60633020, the National Key
Technologies R&D Program of China under Grant
Nos. 2006BAK11B02,2006BAJ07B06.
REFERENCES
Alvarez M., Raposo J., Pan, A., Cacheda, F., Bellas, F.,
Carneiro, V, (2007). DeepBot: A Focused Crawler for
Accessing Hidden Web Content, In
Proceedings of
DEECS2007
. San Diego CA, pages.18-25.
Barbosa L. and Freire J. (2005). Searching for Hidden
Web Databases. In
Proceedings of WEBDB2005,
Baltimore MD, pages.1-6.
Barbosa L. and Freire J. (2004). Siphoning Hidden-Web
Data through Keyword-Based Interfaces. In Proceed-
ings of SBBD2004
, Brasilia Brazil, pages. 309-321.
He B., Chang K. C. C (2006). Automatic Complex
Schema Matching across Web Query Interfaces: A
Correlation Mining Approach.
ACM Transactions on
Database Systems
, vol. 13, pages.1-45.
Ipeirotis P., Gravano L. (2002). Distributed Search over
the Hidden Web: Hierarchical Database Sampling and
Selection. In
Proceedings of VLDB2002, Hong Kong
China, August, pages. 1-12.
Kenneth W. Church and William. (1995). A. Gale.
Poisson Mixtures.
Natural Language Engineering,
vol. 1, pages 163-190.
Mandelbrot B. B. (1988). The Fractal Geometry of Nature.
New York: W. H. Freeman and Company.
Michael K. Bergman. (2001). The Deep Web: Surfacing
Hidden Value.
The Journal of Electronic Publishing
from the University of Michigan, vol. 7, pages 3-21.
Ntoulas A., Zerfos P., Cho J. Downloading Textual
Hidden Web Content through Keyword Queries. In
Proceedings of JCDL2005, Denver CO, June 2005,
pages 100-109.
Raghavan S. and Garcia-Molina H. (2001). Crawling the
Hidden Web. In Proceedings of VLDB2001, Rome
Italy, pages 129-138.
Wu P., Wen J. R., Liu H., Ma W. Y. (2006). Query
Selection Techniques for Efficient Crawling of
Structured Web Source. In
Proceedings of ICDE2006,
Atlanta GA, pages 47-56.
Zhang Z., He B., Chang K. C. C. (2006). Understanding
Web Query Interfaces: Best Effort Parsing with
Hidden Syntax. In
Proceedings of the ACM
SIGMOD2004
, Paris France, pages 107-118.
WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies
642
