METHODS AND TOOLS FOR MODELLING REASONING

IN DIAGNOSTIC SYSTEMS

Alexander P. Eremeev and Vadim N. Vagin

Moscow Power Engineering Institute (Technical University), Krasnokazarmennaya 14, 111250, Moscow, Russia

Keywords: Artificial intelligence, Decision support, Expert diagnostic system, Assumption-based truth maintenance

system, Case-based reasoning, Knowledge base.

Abstract: The methods of case-based reasoning for a solution of problems of real-time diagnostics and forecasting in

intelligent decision support systems (IDSS) is considered. Special attention is drawn to a case library

structure for real-time IDSS and an application of this reasoning type for diagnostics of complex object

states. The problem of finding the best current measurement points in model-based device diagnostics with

using Assumption-based Truth Maintenance Systems (ATMS) is viewed. The new heuristic approaches of

current measurement point choosing on the basis of supporting and inconsistent environments are presented.

This work was supported by the Russian Foundation for Basic Research (projects No 08-01-00437 and

No 08-07-00212).

1 INTRODUCTION

The problem of human reasoning simulating (so

called “common sense” reasoning) in artificial

intelligence systems and especially in intelligent

decision support systems (IDSS) is very actual

nowadays (Vagin, 2007). That is why special

attention is turned to case-based reasoning methods

and heuristic methods of obtaining the effective

measurement in diagnostic systems on the basis of

ATMS. The precedents (cases) can be used in

various applications of artificial intelligence (AI)

and for solving various problems, e.g., for

diagnostics and forecasting or for machine learning.

At first we consider case-based reasoning (CBR)

methods including four main stages that form a

CBR-cycle and the application of CBR for

diagnostics of complex object states. Then model-

based diagnostics on the basis of ATMS and

heuristic methods of choosing a measurement point

in a diagnosed device are viewed. And finally

modeling results of the best measurement point

choosing for the 9-bit parity checker are given.

2 CASE-BASED REASONING

Case-based reasoning is an approach that allows to

solve a new problem using or adapting a solution of

a similar well-known problem (Eremeev, 2006). As

a rule, case-based reasoning methods include four

main stages that form a CBR-cycle, the structure of

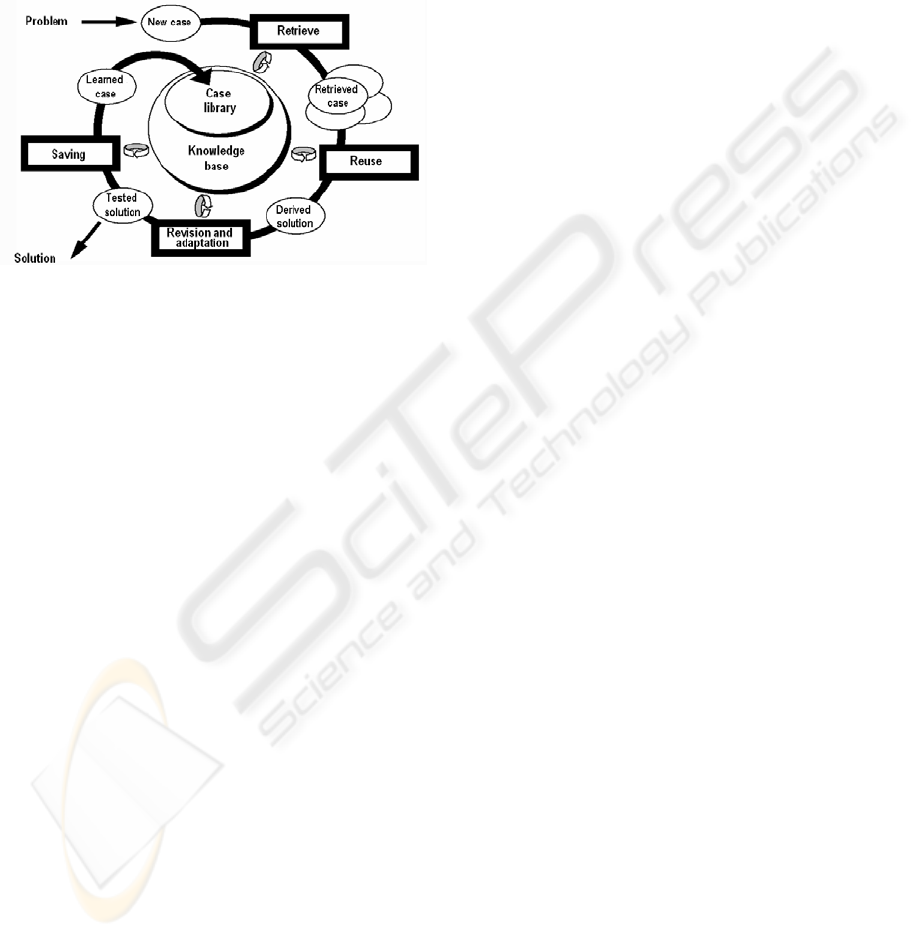
which is represented in figure 1.

The main stages of CBR-cycle are the following

(Aamodt, 1994; Eremeev, 2007).

• Retrieving the closest (most similar) case (or

cases) for the situation from the case library;

• Using the retrieved case (precedent) for solving

the current problem;

• If necessary, reconsidering and adaptation of the

obtained result in accordance with the current

problem;

• Saving the newly made solution as part of a new

case.

It is necessary to take into account that a solution

on the basis of cases may not attain the goal for the

current situation, e.g., in the absence of a similar

(analogous) case in the case library. This problem

can be solved if one presupposes in the CBR-cycle

the possibility to update the case library in the

reasoning process (inference). A more powerful (in

detecting new facts or new information) method of

reasoning by analogy is means of updating case

libraries.

Use of the mechanism of cases for IDSS of real

time (RT IDSS) consists in issuing the decision to

the operator (DMP – Decision Making Person) for

271

P. Eremeev A. and N. Vagin V. (2009).

METHODS AND TOOLS FOR MODELLING REASONING IN DIAGNOSTIC SYSTEMS.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

271-276

DOI: 10.5220/0001832902710276

 SciTePress

the current situation on the basis of cases which are

contained in a system. As a rule, the last stage in a

CBR-cycle is excluded and performed by an expert

(DMP) because the case library should contain only

reliable information confirmed by an expert.

Reconsidering and adaptation of the taken decision

is required seldom because the same object

(subsystem) is considered.

Figure 1: CBR-cycle.

The modified CBR-cycle for RT IDSS includes

the following stages:

• Retrieving the closest (most similar) case (or

cases) for the situation from the case library;

• Using the retrieved case (precedent) for solving

the current problem.

• Case-based reasoning for IDSS consists in

definition of similarity degree of the current

situation with cases from case library. For

definition of similarity degree, the nearest

neighbor algorithm (k-nearest neighbor algorithm)

is used.

There was built the structure of case library for

RT IDSS on the basis of non-classical logics for

monitoring and control of complex objects like

power units.

The case library for RT IDSS should join in itself

the cases concerning a particular subsystem of a

complex object, and also contain the information on

each parameter which is used for the description of

cases (parameter type and range). Besides, the case

library should include such adjustments, as:

• the significance of a parameter;

• a threshold value of similarity;

• a value which limits quantity of considered cases.

It is necessary to emphasize, that the case library

can be formed on the basis of:

• the experience, accumulated by an expert;

• analysis of the system archive;

• analysis of emergencies;

• operative instructions;

• technological requirements.

The case library can be included in the structure

of the knowledge base of RT IDSS or act as a

separate component of the system.

3 APPLICATION OF

CASE-BASED REASONING

FOR DIAGNOSTICS OF

COMPLEX OBJECT STATES

As a complex object, we shall understand an object

which has a complex architecture with various

interrelations, with a lot of controllable and operated

parameters and small time for acceptance of

operating influences. As a rule, such complex

objects like the power unit are subdivided into

technological subsystems and can function in

various modes (in regular, emergency, etc.).

For the description of such complex object and

its subsystems, a set of parameters is used. The state

of an object is characterized by a set of concrete

values of parameters.

In the operative mode, reading of parameter

values from sensors for the whole object is made by

the system of controllers with an interval at 4

seconds. For this time interval, it is necessary to give

out to the DMP (operator) the diagnosis and the

recommendation on the developed situation.

Diagnosing and detection of operating influences

is carried out on the basis of expert knowledge,

technological requirements and operative

instructions. The developed software (Case Library

Constructor – CLC) can be applied to the decision of

the specified problems.

Basic components of CLC are:

• module for storage and loadings case libraries and

for data import;

• a subsystem of visualization for browsing the

structure of case libraries;

• a subsystem of editing and adjustment of case

libraries;

• a module of new cases check;

• a subsystem of case library testing and case-based

reasoning.

CLC was implemented in Borland C++ Builder

6.0 for Windows NT/2000/XP.

Implementation of case libraries with use of

CLC for systems of expert diagnosing is

subdivided

into the following main stages:

ICEIS 2009 - International Conference on Enterprise Information Systems

272

• Creation of case libraries for subsystems of

complex object;

• Adjustment of the created case libraries;

• Addition of cases in case libraries;

• Check of the added cases;

• Testing of the filled case libraries with using case-

based reasoning;

• Reservation of the created case libraries for their

subsequent transfer to operative maintenance.

This tool was applied in the prototype of a RT

IDSS for monitoring and control of complex objects

like power units on an example of a pressurizer in

pressurized water reactor (PWR) of the atomic

power station (Eremeev, 2008).

4 MODEL-BASED DIAGNOSTICS

The generalized problem of diagnostics can be

formulated as follows. There is a device exhibiting

an incorrect behaviour. The device will consist of

components, one or several of which are not

working properly what is the reason of incorrect

behaviour. There is a structure of connections

between components and a possibility to get

measurements on their inputs and outputs. It is

necessary to determine what of components are

faulty with minimal resource expenses.

At present two main approaches to a solution of

the given problem are viewed (Clancey, 1985; de

Kleer, 1987; Forbus, 1993).

The first approach is heuristic diagnostics. The

base of this approach is the knowledge extraction

from an expert and building fault determining rules

in the form of "symptoms → faults".

Because this approach suffers from a rigid

dependence on a device structure and difficulties

using the knowledge bases for other diagnostic

problems we use the second approach – so called

model-based diagnostics. This approach is based on

the knowledge of device component functionality.

The model of a device is a description of its

physical structure, plus the models for each of its

components. A compound component is a

generalized notion including simple components,

processes and even logical inference stages.

Model-based diagnosis process is the comparison

of predicted device behaviour with its observed

behaviour.

It is supposed, that the model is correct, and all

differences between device behaviour and a device

model indicate availability of broken components.

Main advantages of the model-based approach:

• diagnosing the multiple faults;

• unexpected fault recognition;

• a precision of a component model description does

not depend on the expert experience;

• a possibility of new device diagnosing;

• multiple using the models;

• detailed explanations.

5 ASSUMPTION-BASED TRUTH

MAINTENANCE SYSTEMS

For building a prognosis network, a component

behaviour model, finding minimal conflicts

characterizing mismatch of observations with

prognoses and candidates for a fault, it is efficient to

use possibilities given by ATMS (de Kleer, 1986;

Vagin, 2008).

The truth maintenance systems (TMS) are the

systems dealing with the support of coherence in

databases. They save the assertions transmitted to

them by a problem solver and are responsible for

maintaining their consistency. Each assertion has the

justification describing what kind of premises and

assumptions this justification was obtained. The

environment is a set of assumption.

The inference of an inconsistency characterizes

assumption incompatibility within the

presuppositions of which this conclusion was made.

Also there is introduced the environment set which

contains some inconsistency (de Kleer, 1986). The

sets of inconsistency environments E

, ..., E

are

Nogood = {E

, E

, ..., E

). A consistent ATMS

environment is not Nogood.

There are the following correspondences

between ATMS and the model-based diagnosis

approach:

• ATMS premises – an observed device behaviour;

• ATMS assumptions – components of a device;

• inferred ATMS nodes – predictions of an

diagnostic system;

• Nogood – the difference between predicted and

observed device behaviour.

6 THE CURRENT

MEASUREMENT POINT

DETERMINATION

One of the key aspects of the model-based fault

search algorithm is to determine the optimal current

measurement in a diagnosed device. Efficiency of

METHODS AND TOOLS FOR MODELLING REASONING IN DIAGNOSTIC SYSTEMS

273

the current measurement choosing allows essentially

reducing a decision search space while the

inefficiency of choice will increase an operating

time, the space of a searching algorithm, and also

require additional resource spends to implement a

measurement.

The best measurement point in a diagnosed

device is a place (point) of measuring a value giving

the largest information promoting the detection of a

set of fault components at minimal resource

spending.

One of the best procedures for reducing resource

expenses is to produce the measuring giving the

maximal information concerning predictions made

on the basis of the current information on a system.

6.1 Heuristic Methods of Choosing

a Measurement Point

The purpose of the best choosing a measurement

point is to derive the maximal component state

information. After each measuring there is a

confirmation or refutation of prediction values in a

point of measurement. So, it is possible to use the

following aspects:

• Knowledge about environments that support

predicted values in the measurement points which

can be confirmed or refuted.

• Knowledge about inconsistent environments.

• Knowledge about coincided assumptions of the

inconsistent environments.

6.2 Knowledge about Supporting

Environments

The diagnostic procedure constructs predictions of

values for each device point with the list of

environments in which the given prediction is held.

The list of environments represents assumption sets

about correctness of corresponding device

components. As we are interested with a

measurement point with the greatest information on

failure, a point is selected from a quantity of

assumptions. Let’s introduce the function Quan(x),

by which we will designate the information quantity

obtained at measuring values in the point x. The

points with the greatest value of this function have

the greatest priority of a choice. We will call the

given method of choosing a measurement points as

SHE (Supporting Environment Heuristics).

6.3 Knowledge about the Sets

of Inconsistent Environment

As a result of each measurement there is a

confirmation or refutation of some prediction. The

environments E

, E

, ..., E

of refuted prediction

form the set Nogood = {E

, E

, ..., E

}. It can be

used for directional searching for more precise

definition what kind of components from Nogood is

broken.

Obviously the more of the components from

Nogood are specified by measuring a value in some

device point the more the information about which

components of Nogood are broken will be obtained.

Designate an environment set as Envs (x). For using

this possibility, it is necessary to take the

intersection of each environment from Envs(x) with

each set from Nogood:

Envs(x) ∩ Nogood = {A ∩ B: A ∈ Envs(x), B ∈

Nogood}.

Points with the greatest value of a variety of the

function Quan(x) have the greatest priority of a

choice. We will call the given method of choosing a

measuring point as SIEH (Supporting and

Inconsistent Environment Heuristics).

6.4 Knowledge about Coincided

Assumptions of the Inconsistent

Environments

During diagnostics of faulty devices as a result of

confirmations and refutations of some predictions

there is a modification of a set of inconsistent

environments Nogood.

In each component set from Nogood one or more

components are broken what was a reason of

including a supporting set into the inconsistent

environments Nogood. Taking the intersection of all

sets of the inconsistent environments, we receive a

set of components which enter into each of them, so

their fault can be a reason explaining an

inconsistence of each set holding in Nogood. Thus,

we obtain the list of components a state of which is

recommended to test first of all, i.e. the most

probable candidates on faultiness.

The set intersection of inconsistent environments

is expressed by the following equation:

∩

NogoodE

EodSingleNogo

∈

If SingleNogood = ∅, it means that there are

some disconnected faults. In this case the given

approach is inapplicable and it is necessary to define

ICEIS 2009 - International Conference on Enterprise Information Systems

274

more precisely the further information by any other

methods.

After obtaining a set SingleNogood

≠

∅, on the

base of environments of value predictions in device

points it is necessary to select those measurement

points that allow to effectively test components to be

faulted from SingleNogood.

For this purpose we will work with the sets

obtained as a result of an intersection of each

environment from Envs(x) with SingleNogood:

Envs(x) ∩ SingleNogood = {J ∩ SingleNogood: J ∈

Envs{x)}.

The following versions are possible:

a) ∃ J ∈ Envs(x): J ≡ SingleNogood. One of

environments of the value prediction in the point

x coincides with the set SingleNogood. The given

version allows to test faulty components from the

set SingleNogood most effectively so this

measurement point x is selected with the most

priority.

b) ∃ J ∈ Envs(x): |J ∩ SingleNogood| < |SingleNog

ood|. The cardinality of SingleNogood is more

than the cardinality of a set obtaining as a result

of an intersection SingleNogood with a set from

Envs(x). We evaluate this version as

||max

)(

odSingleNogoJ

xEnvsJ

∩

∈

, i.e. the more of

components from SingleNogood are intersected

with any environment from Envs(x), the more

priority of a choice of the given measurement

point for the observation.

c) ∃ J ∈ Envs(x): SingleNogood

⊂

J. The

SingleNogood includes in a set from Envs(x). We

evaluate this version as

|)||(|min

)(

odSingleNogoJ

xEnvsJ

−

∈

, i.e. the less a

difference between SingleNogood and Envs(x),

the more priority of a choice of the given

measurement point for the current observation.

d) ∀ J ∈ Envs(x):J ∩ SingleNogood = ∅, i.e. no one

of the most probable faulty candidates includes

in environments Envs(x) supporting predictions

at the point x. We evaluate this version as the

least priority choice, i.e. 0 in the numerical

equivalent.

Also to the version D there are referred other

methods of definition of current measurement point

priorities which happen when SingleNogood = ∅.

Thus, in the estimations of a choice priority a

numerical value returned as a result of call of other

method is accepted. We call it by ResultD(x).

At appearance of the greater priority choosing

between versions B and C, heuristically we accept

the version B as at this choice the refinement of

faulty candidates is produced better.

Note for various supporting sets of the same

Envs(x), the availability of both the version B and

the version C is also possible. In this case, as a

resulting estimation for the given Envs(x) the version

B is also accepted.

We will call the method of choosing the place

where reading is taken by the heuristics based on the

set of supporting and coinciding assumptions of

inconsistent environments as SCAIEH (Supporting

and Coinciding Assumptions of Inconsistent

Environment Heuristics).

The developed methods of heuristic choice of the

best current measurement point are recommended to

use for devices with a great quantity of components

as quality of guidelines directly depends on the

quantitative difference of environments.

7 PRACTICAL RESULTS

Let's test the developed methods of the best

measurement point choosing for the 9-bit parity

checker (Frohlich, 1998).

For each experiment one of device components

is supposed working incorrectly what is exhibited in

a value on its output opposite predicted. A

consequence of the incorrect component work is

changing of outputs of those components which

produce the results depending on values on the

output of a faulty component. These changed results

of component operations are transmitted to

appropriate inquiries of a diagnostic system.

In figure 2 the quantity of the stages required to

each method for fault localization is shown. A

method stage is a measurement point choosing. The

smaller the quantity of method stages, the faster a

fault is localized.

From the obtained results one can see that the

method efficiency for different fault components is

various and hardly depends on the device structure.

Let's estimate the method efficiency. The device

is consists of 46 components. The output values of

45 components are unknown (a value on the output

of Nor5 is transmitted to the diagnostic system with

input data together). So, the maximal stage quantity

necessary for a fault definition is equal 45. Let's

accept 45 stages as 100 %. For each experiment it is

computed on how many percents each of the

developed methods is more effective than exhaustive

search of all values. Then define the average value

of results. The evaluated results are represented in

table 1.

METHODS AND TOOLS FOR MODELLING REASONING IN DIAGNOSTIC SYSTEMS

275

Figure 2: The quantity of the stages required to each

method.

Table 1: Evaluated results.

The method SEH SIEH SCAIEH

On how many percents

the method is more effective, %

30,79 63,17 68,65

From table 1 one can see that the greatest

efficiency of current measurement point choosing

has the heuristic method based on the knowledge

about coincided assumptions of the inconsistent

environments SCAIEH.

8 CONCLUSIONS

The method of case-based reasoning was considered

from the aspect of its application in modern IDSS

and RT IDSS, in particular, for a solution of

problems of real-time diagnostics and forecasting.

The CBR-cycle is viewed and its modification for

application in RT IDSS is offered. The k-nearest

neighbor algorithm for definition of similarity

degree of a current situation with cases from a case

library is supposed. Note that elements of case-based

reasoning may be used successfully in analogy-

based reasoning methods, i.e., these methods

successfully compliment each other and their

integration in IDSS is very promising.

Also the heuristic methods of finding the best

current measurement point based on environments

of device components work predictions are

presented.

Practical experiments have confirmed the

greatest efficiency of current measurement point

choosing for the heuristic method based on the

knowledge about coincided assumptions of the

inconsistent environments SCAIEH.

Advantages of heuristic methods of the best

current measurement point choosing is the simplicity

of evaluations and lack of necessity to take into

consideration the internal structure interconnections

between components of a device.

REFERENCES

Vagin V.N., Yeremeyev A.P., 2007. Modeling Human

Reasoning in Intelligent Decision Support Systems //

Proc. of the Ninth International Conference on

Enterprise Information Systems. Volume AIDSS.

Funchal, Madeira, Portugal, June 12-16, INSTICC,

pp.277-282.

Eremeev, A., Varshavsky, P., 2006. Analogous Reasoning

and Case-Based Reasoning for Intelligent Decision

Support Systems // International Journal

INFORMATION Theories & Applications (ITHEA),

vol. 13 № 4, pp. 316-324.

Aamodt, E., 1994. Plaza “Case-Based Reasoning:

Foundational Issues, Methodological Variations, and

System Approaches” // AI Communications, No. 7.

Eremeev, A., Varshavsky, P., 2007. Application of Case-

based Reasoning for Intelligent Decision Support

Systems // Proceedings of the XIII

International

Conference “Knowledge-Dialogue-Solution” – Varna,

vol. 1, pp. 163-169.

Eremeev, A., Varshavsky, P., 2008. Case-based Reasoning

Method for Real-time Expert Diagnostics Systems //

International Journal “Information Theories &

Applications”, Volume 15, Number 2, pp. 119-125.

Clancey W., 1985. Heuristic Classification. // Artificial

Intelligence, 25(3), pp. 289-350.

de Kleer, J. and Williams, B.C., 1987. Diagnosing

Multiple Faults. // Artificial Intelligence, v.32, pp. 97-

130.

Forbus K.D., de Kleer, J., 1993. Building Problem Solver.

// A Bradford Book, The MIT Press, Cambridge,

Massachusetts, London, England.

de Kleer J., 1986. An Assumption-based TMS. // Artificial

Intelligence, v.28, p.127-162.

Vagin V.N., Golovina E.Ju., Zagoryanskaya A.A., Fomina

M.V., 2008. Exact and Plausible Inference in

Intelligent Systems. 2

edition. // Vagin V.N.,

Pospelov D.A. (eds). M.: Fizmatlit, – 710 p. (in

Russian).

Frohlich P., 1998. DRUM-II Efficient Model-based

Diagnosis of Technical Systems. //PhD thesis,

University of Hannover.

ICEIS 2009 - International Conference on Enterprise Information Systems

276