CONTEXT-AWARE RANKING ALGORITHMS IN FOLKSONOMIES

Fabian Abel, Nicola Henze and Daniel Krause

IVS – Semantic Web Group, Leibniz University Hannover, Appelstr. 4, 30167 Hannover, Germany

Keywords:

Social Media, Search, Ranking, Folksonomies, GroupMe!

Abstract:

Folksonomy systems have shown to contribute to the quality of Web search ranking strategies. In this paper,

we analyze and compare graph-based ranking algorithms: FolkRank and SocialPageRank. We enhance these

algorithms by exploiting the context of tags, and evaluate the results on the GroupMe! dataset. In Group-

Me!, users can organize and maintain arbitrary Web resources in self-deﬁned groups. When users annotate

resources in GroupMe!, this can be interpreted in context of a certain group. The grouping activity itself is easy

for users to perform: simple drag-and-drop operations allow users to collect and group resources. However, it

delivers valuable semantic information about resources and their context. We show how to use this information

to improve the detection of relevant search results, and compare different strategies for ranking result lists in

folksonomy systems.

1 INTRODUCTION

Social interactions, participation in the content cre-

ation process, easy-to-use applications – these are

among the usage characteristics of currently success-

ful, so-called Web 2.0-applications. Users in Web

2.0 applications are more than ever active in the con-

tent life-cycle: They contribute with their opinion

by annotating Web content (the so-called tagging),

they add and annotate content (e.g. by using appli-

cations for sharing their bookmarks, pictures, videos,

etc. with other users), they rate content, and they cre-

ate content (e.g. with sorts of online dictionaries, so-

called blogs). In this paper, we focus on the ﬁrst type

of applications: social tagging systems. In a social

tagging system, users tag Web content, share these

tags with other users of the application, and proﬁt by

the tagging activity of the whole user community by

discovering / retrieving relevant Web content during

browsing / as answers to search queries. The tagging

activities are modeled in a folksonomy (Vander Wal,

2007): a taxonomy, which evolves over time when

users (the folks) annotate resources with freely chosen

keywords. Folksonomies can be divided into broad

folksonomies, which allow different users to assign

the same tag to the same resource, and narrow folk-

sonomies, in which the same tag can be assigned to a

resource only once.

Bao et al. showed that Web search can be im-

proved by exploiting knowledge embodied in folk-

sonomies (Bao et al., 2007). In this paper, we in-

troduce and evaluate different ranking strategies for

folksonomy systems. In particular, we

• propose an algorithm, which exploits the context

gained by grouping resources in folksonomy sys-

tems and which improves search for resources:

GRank.

• compare existing ranking algorithms for folk-

sonomies: FolkRank and SocialPageRank. We

extend these algorithms and propose (a) group-

sensitive FolkRank algorithms, and (b) a topic-

sensitive SocialPageRank algorithm, and evaluate

their quality with respect to search tasks.

The paper is organized as follows. In the next sec-

tion we discuss our work with respect to related work.

In Section 3, we brieﬂy introduce the functionality of

the GroupMe! system. Section 4 presents a formal

deﬁnition of folksonomies, and their extension with

group structures. Afterwards, we identify the charac-

teristics of the folksonomy, which builds the dataset

of the GroupMe! application. Different folksonomy-

based ranking strategies are discussed in the follow-

ing section. Section 6 presents our evaluation results.

The paper ends with conclusions.

2 RELATED WORK

In this paper we enhance ranking algorithms for folk-

sonomies. We extend the FolkRank algorithm intro-

duced in (Hotho et al., 2006b) with the capability of

167

Abel F., Henze N. and Krause D.

CONTEXT-AWARE RANKING ALGORITHMS IN FOLKSONOMIES.

DOI: 10.5220/0001838601670174

In Proceedings of the Fifth International Conference on Web Information Systems and Technologies (WEBIST 2009), page

ISBN: 978-989-8111-81-4

exploiting additional context information gained by

GroupMe! folksonomies. Furthermore, we improve

SocialPageRank (Bao et al., 2007) by enabling topic-

sensitive rankings. In our experiment we evaluate

ranking of resources whereas in (Abel et al., 2008a)

we focussed on ranking tags and evaluated the quality

of different graph-based ranking algorithms with re-

spect to tag recommendations. In (Sigurbj

ornsson and

van Zwol, 2008) the authors propose an approach for

recommending tags, which is based on co-occurences

of tags. However, our evaluations in (Abel et al.,

2008a) indicate that graph-based recommender algo-

rithms are more appropriate for folksonomies than

strategies as described in (Sigurbj

ornsson and van

Zwol, 2008).

When designing algorithms for folksonomy sys-

tems, the basic assumption is that tags describe the

content of resources very well. In (Li et al., 2008) the

authors prove this assumption by comparing the ac-

tual content of web pages with tags assigned to these

websites in the del.icio.us

system.

3 GROUPME! FOLKSONOMY

SYSTEM

The GroupMe!

Folksonomy System (Abel et al.,

2007) is a fun-to-use Web 2.0 application. It is a

resource sharing system like del.icio.us or Bibson-

omy

, offering the extended feature of grouping Web

resources. These GroupMe! groups can contain ar-

bitrary multimedia resources like websites, photos or

videos, which are visualized according to their media

type: E.g., images are displayed as thumbnails and

the headlines from RSS feeds are structured in a way

that the most recent information are accessible by just

one click. With this convenient visualization strategy,

the user can grasp the content immediately without

the need of visiting the original Web resource. Fig-

ure 1 shows a group about WEBIST 2009 in Lisbon,

which contains the website of the conference, a video

with traveling information about Lisbon, a GroupMe!

group about the last WEBIST conference, etc.

GroupMe! groups are created by dragging &

dropping multimedia resources from various sources

into a group (cf. Figure 1). We also offer a book-

marklet to add the currently visited Web site with a

single click into the GroupMe! system. Building

groups is a very convenient way of aggregating con-

tent. As groups are also normal Web resources, it is

http://del.icio.us

http://groupme.org

http://bibsonomy.org

Figure 1: GroupMe! group about WEBIST ’09 available at

http://groupme.org/GroupMe/group/2671.

possible to group groups and hence, to model hierar-

chies.

To foster Semantic Mashups, all data collected by

the GroupMe! system is available in different for-

mats: For a lightweight integration, we offer RSS

feeds, which enable users easily to get informed if

new content is added to a group. Furthermore, we of-

fer an RDF based RESTful API, which enables other

applications to navigate through the semantically en-

riched GroupMe! data corpus according to the princi-

ples of Linked Data.

4 FOLKSONOMIES

Formally, folksonomies are deﬁned as tuples of folk-

sonomy entities, i.e. users, tags, and resources, and

the bindings between these entities, which are called

tag assignments and denote which user has assigned

which tag to a certain resource. According to (Hotho

et al., 2006a), a folksonomy can be deﬁned as

Deﬁnition 1 (Folksonomy). A folksonomy is a

quadruple F := (U, T,R, Y ), where:

• U, T , R are ﬁnite sets of instances of users, tags,

and resources

• Y deﬁnes a relation, the tag assignment, between

these sets, that is, Y ⊆ U × T × R

GroupMe! extends this folksonomy deﬁnition by

the concept of groups:

Deﬁnition 2 (Group). A group is a ﬁnite set of re-

sources.

A group is a resource as well. Groups can be

tagged or arranged in groups, which effects hierar-

chies among resources. In general, tagging of re-

WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies

168

sources within the GroupMe! system is done in con-

text of a group. Hence a GroupMe! folksonomy

is formally characterized via Deﬁnition 3 (cf. (Abel

et al., 2007)).

Deﬁnition 3 (GroupMe! folksonomy). A GroupMe!

folksonomy is a 5-tuple F := (U, T,

R,G,

Y ), where:

• U, T , R, G are ﬁnite sets that contain instances of

users, tags, resources, and groups

•

R = R ∪ G is the union of the set of resources and

the set of groups

•

Y deﬁnes a GroupMe! tag assignment:

Y ⊆ U ×

T ×

R × (G ∪ {ε}), where ε is a reserved symbol

for the empty group context, i.e. a group that is

not contained in another group when it is tagged

by a user

4.1 Folksonomy Characteristics in

GroupMe!

To decide whether known folksonomy search and

ranking algorithms can be improved by considering

the group context, we had a closer look on the tag-

ging and grouping behavior of our users by analyzing

a snapshot of the GroupMe! dataset, which contains

1546 unique tags, 2338 resources, 352 users, 453

groups, and 2690 tag assignments. The ﬁrst question

was whether users made use of the feature of group-

ing and visualizing different media types. In Figure 2

we show the distribution of the different media types

in the GroupMe! system.

Figure 2: Media type distribution in the GroupMe! system.

Our observation is, that users use different medi-

atypes and especially multimedia documents. About

40% of all resources in our system are multimedia

documents, where tags form the main textual descrip-

tion, because extraction of other meta data is barely

possible.

In (Li et al., 2008) the authors show that tags de-

scribe resources very precisely and are hence a valu-

able input for searching and ranking. GroupMe! mo-

tivates users to tag resources by using the free-for-all

tagging approach (see (Marlow et al., 2006)), which

enables users to tag not only their own resources, but

all resources within the GroupMe! system.

Figure 3: Distribution of tag assignments.

On a logarithmic scale (extended with zero), we

plotted the number of tag assignments on the y-axis

and the number of resources having this number of

tags assigned on the x-axis (see Figure 3). We ob-

served a power law distribution of the tag assignments

per resource, while about 50% of all resources do not

even have a single tag assignment. That means, that

50% of all resources in the GroupMe! system can

hardly be found by known folksonomy based search

and ranking algorithms.

5 FOLKSONOMY-BASED

RANKING ALGORITHMS

In this section we present different algorithms, which

target on ranking folksonomy entities. We ﬁrst in-

troduce graph-based algorithms that can be applied

to arbitrary folksonomy entities (users, tags, and re-

sources). In Section 5.2 we describe algorithms,

which speciﬁcally focus on ranking resources to sup-

port e.g. traditional search functionality in folkson-

omy systems.

Our contributions, i.e. ranking algorithms we de-

veloped, can be summarized as follows:

GFolkRank & GFolkRank

. Graph-based rank-

ing algorithms, which extend FolkRank (Hotho

et al., 2006b) and turn it into a group-sensitive

algorithm in order to exploit GroupMe! folk-

sonomies (see Section 5.1.2).

Personalized SocialPageRank . Extension to

SocialPageRank (Bao et al., 2007), which allows

for topic-sensitive rankings.

GRank . A search and ranking algorithm optimized

for GroupMe! folksonomies.

5.1 Universal Ranking Strategies

Universal ranking strategies like FolkRan and Group-

sentitive FolkRank can be used to rank arbitrary parts

CONTEXT-AWARE RANKING ALGORITHMS IN FOLKSONOMIES

169

of a folksonomy, e.g. users, resources, tags etc.

5.1.1 FolkRank

FolkRank (Hotho et al., 2006b) adapts Personalized

PageRank (Page et al., 1998) for ranking users, tags,

and resources in traditional folksonomies.

~w ← dA~w + (1 − d)~p (1)

The adjacency matrix A models the folksonomy graph

= (V

). G

is an undirected, weighted tri-

partite graph, which is created from the the folk-

sonomy (cf. Deﬁnition 1). The set of nodes is

= U ∪ T ∪ R and the set of edges is given via

= {{u,t}, {t, r}, {u, r}|(u, t, r) ∈ Y }}. The edges

are weighted according to their frequency within the

set of tag assignments. For example, w(t,r) = |{u ∈

U : (u,t, r) ∈ Y }| denotes the popularity of tag t for

the resource r and counts the number of users, who

have annotated r with t. w(u,t) and w(u, r) are de-

ﬁned accordingly. A is normalized so that each row

has a 1-norm equal to 1. The inﬂuence of the prefer-

ence vector ~p is conﬁgured via d ∈ [0, 1]. Finally, the

FolkRank algorithm is deﬁned as follows (see (Hotho

et al., 2006b)).

Deﬁnition 4 (FolkRank). The FolkRank algorithm

computes a topic-speciﬁc ranking in folksonomies by

executing the following steps:

1. ~p speciﬁes the preference in a topic (e.g. prefer-

ence for a given tag).

2. ~w

is the result of applying the Personalized Page-

Rank with d = 1.

3. ~w

is the result of applying the Personalized Page-

Rank with some d < 1.

4. ~w = ~w

− ~w

is the ﬁnal weight vector. ~w[x] de-

notes the FolkRank of some x ∈ V

When applying FolkRank to GroupMe! folk-

sonomies (see Deﬁnition 3) a straightforward ap-

proach is to ignore the group dimension of GroupMe!

tag assignments. Therewith, the construction of the

folksonomy graph G

= (V

) has to be adapted

slightly. The set of nodes is given by V

= U ∪ T ∪

and E

= {{u,t},{t,r}, {u, r}|u ∈ U,t ∈ T, r ∈

R,g ∈

G∪{ε}, (u,t,r, g) ∈

Y } deﬁnes the set of edges. Com-

putation of weights is done correspondingly to the

FolkRank algorithm, e.g. w(t,r ) = |{u ∈ U : g ∈

G ∪ {ε}, (u,t, r, g) ∈

Y }| is the number of users, who

annotated resource r with tag t in any group.

5.1.2 Group-sensitive FolkRank (GFolkRank)

The traditional FolkRank does not make use of the

additional structure of GroupMe! groups. In (Abel

et al., 2008b) we propose different adaptations of

FolkRank, which exploit group structures in folk-

sonomies, and show that they improve the ranking

quality of FolkRank signiﬁcantly (one-tailed t-test,

signiﬁcance level α = 0.05). In this paper we present

one of these strategies, which we call GFolkRank.

GFolkRank interprets groups as artiﬁcial, unique

tags. If a user u adds a resource r to a group g

then GFolkRank interprets this as a tag assignment

(u,t

,r,ε), where t

∈ T

is the artiﬁcial tag that iden-

tiﬁes the group. The folksonomy graph G

is ex-

tended with additional vertices and edges. The set

of vertices is expanded with the set of artiﬁcial tags

: V

= V

∪ T

. Furthermore, the set of edges E

is augmented by E

= E

∪{{u,t

},{t

,r}, {u, r}|u ∈

U,t

∈ T

,r ∈

R, u has added r to group g}. The new

edges are weighted with a constant value w

as a re-

source is usually added only once to a certain group.

We select w

= 5.0 ≈ max(|w(t,r)|) because we be-

lieve that grouping a resource is, in general, more

valuable than tagging it. GFolkRank is consequently

the FolkRank algorithm (cf. Section 5.1.1), which op-

erates on basis of G

= (V

GFolkRank

denotes a strategy that extends

GFolkRank with the feature of propagating tags,

which have been assigned to a group, to its resources.

The weight of edges e ∈ E

, which are caused by such

inherited tag assignments, is adjusted by a dampen

factor d f ∈ [0,1]. For our evaluations in Section 6 we

set d f = 0.2.

5.2 Ranking Resources

In contrast to the FolkRank-based algorithms, which

can be utilized to rank all types of folksonomy en-

tities – i.e. users, tags, resources, and groups – we

present SocialPageRank (Bao et al., 2007) and pro-

pose GRank, which is a search and ranking algorithm

optimized for GroupMe! folksonomies. Both algo-

rithms concentrate on ranking resources.

5.2.1 SocialPageRank

The SocialPageRank algorithm (Bao et al., 2007) is

motivated by the observation that there is a strong in-

terdependency between the popularity of users, tags,

and resources within a folksonomy. For example, re-

sources become popular when they are annotated by

many users with popular tags, while tags, on the other

hand, become popular when many users attach them

to popular resources.

SocialPageRank constructs the folksonomy graph

similarly to FolkRank. However, G

is modeled

within three different adjacency matrices. A

T R

mod-

els the edges between tags and resources. The weight

WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies

170

w(t,r ) is computed as done in the FolkRank algorithm

(cf. Section 5.1.1): w(t,r) = |{u ∈ U : (u,t,r) ∈ Y }|.

The matrices A

and A

describe the edges be-

tween resources and users, and users and tags respec-

tively. w(r, u) and w(u,t) are again determined corre-

spondingly. The SocialPageRank algorithm results in

a vector~r, whose items indicate the social PageRank

of a resource.

Deﬁnition 5 (SocialPageRank). The SocialPage-

Rank algorithm (see (Bao et al., 2007)) computes a

ranking of resources in folksonomies by executing the

following steps:

1. Input: Association matrices A

T R

, A

, and

a randomly chosen SocialPageRank vector~r

2. until~r

converges do:

(a) ~u

= A

·~r

(b)

= A

·~u

(c)

= A

T R

(d)

= A

T R

(e)

= A

(f) ~r

i+1

= A

3. Output: SocialPageRank vector~r.

SocialPageRank and FolkRank both base on the

PageRank algorithm. Regarding the underlying ran-

dom surfer model of PageRank (Page et al., 1998),

a remarkable difference between the algorithms re-

lies on the types of links that can be followed by the

“random surfer”. SocialPageRank restricts the “ran-

dom surfer” to paths in the form of resource-user-tag-

resource-tag-user, whereas FolkRank is more ﬂexible

and allows e.g. also paths like resource-tag-resource.

5.2.2 Personalized SocialPageRank

SocialPageRank computes a global ranking of re-

sources in folksonomies. With the Personalized

SocialPageRank algorithm we extend SocialPage-

Rank introduced in (Bao et al., 2007) and transform

into a topic-sensitive ranking algorithm. Therefor, we

introduce the ability of emphasizing weights within

the input matrices of SocialPageRank so that prefer-

ences can be considered, which are possibly adapted

to a certain context. For example, w(t, r) is adapted

as follows: w(t,r) = pre f (t) · pre f (r) · |{u ∈ U :

(u,t,r) ∈ Y }|, where pre f (·) returns the preference

score of t and r respectively. The preference function

pre f (·) is speciﬁed in equation 2:

pre f (x) =



1,if there is no preference in x

c > 1,if there is a preference in x

(2)

In our evaluations (see Section 6) we utilized the

Personalized SocialPageRank in order to align the

SocialPageRank to the context of a keyword query t

and speciﬁed a preference into t

using c = 20.

5.2.3 GroupMe! Ranking Algorithm (GRank)

The most important application of ranking algorithms

is search. In Deﬁnition 6 we introduce GRank, a

search and ranking algorithm optimized for Group-

Me! folksonomies.

Deﬁnition 6 (GRank). The GRank algorithm com-

putes a ranking for all resources, which are related to

a tag t

with respect to the group structure of Group-

Me! folksonomies (see Deﬁnition 3). It executes the

following steps:

1. Input: keyword query tag t

∪

, where:

(a)

contains resources r ∈

R with w(t

,r) > 0

(b)

contains resources r ∈

R, which are con-

tained in a group g ∈ G with w(t

,g) > 0

(c)

contains resources r ∈

R that are contained

in a group g ∈ G, which contains at least one

resource r

∈

R with w(t

) > 0 and r 6= r

(d)

contains groups g ∈ G, which contain re-

sources r

∈

R with w(t

) > 0

3. ~w

is the ranking vector of size |

|, where

(r) returns the GRank of resource r ∈

4. for each r ∈

do:

(a) ~w

(r) = w(t

,r) · d

(b) for each group g ∈ G ∩

do:

(r) + = w(t

,g) · d

∈

where r

is contained in a

same

group as r and r 6= r

do:

(r) + = w(t

) · d

(d) if(r ∈ G) then:

for each r

∈

where r

is contained in r

do:

(r) + = w(t

) · d

5. Output: GRank vector ~w

w(t

,r) is the weighting function deﬁned in Sec-

tion 5.1.1 and counts the number of users, who have

annotated resource r ∈

R with tag t

in any group.

When dealing with multi-keyword queries, GRank

accumulates the different GRank vectors. The fac-

tors d

, d

, and d

allow to emphasize the weights

gained by (a) directly assigned tags, (b) tags assigned

to a group the resource is contained in, (c) tags as-

signed to neighboring resources, and (d) tags assigned

to resources of a group. For the evaluations in Section

6 we set d

= 10, d

= 4, d

= 2, and d

= 4.

CONTEXT-AWARE RANKING ALGORITHMS IN FOLKSONOMIES

171

Table 1: Feature overview of the different ranking strategies

presented in Section 5.1 and Section 5.2.

Ranking applicable topic- group-

Strategy for sensitive sensitive

FolkRank (Hotho et al., 2006b) u, t, r yes no

GFolkRank u, t, r yes yes

GFolkRank

u, t, r yes yes

SocialPageRank (Bao et al., 2007) r no no

Pers. SocialPageRank r yes no

GRank r yes yes

5.3 Synopsis

Table 1 summarizes some features of the ranking

strategies presented in the previous sections. The

FolkRank-based algorithms are applicable for rank-

ing of arbitrary folksonomy entities, i.e. users, tags,

and resources. Furthermore, they are topic-sensitive,

which claims that they do not compute a static rank-

ing but allow to adapt rankings to a certain context.

SocialPageRank computes static, global rankings in-

dependent of the context, which is e.g. given by a

keyword query. With Personalized SocialPageRank

we transformed SocialPageRank into a topic-sensitive

ranking algorithm. GFolkRank, GFolkRank

, and

GRank denote search and ranking strategies, which

exploit group structures of GroupMe! folksonomies

(cf. Deﬁnition 3) and are therewith group-sensitive.

6 EVALUATIONS

The most important application for ranking algo-

rithms is search. Therefor, we evaluated the algo-

rithms presented in Section 5 with respect to search

for resources within the GroupMe! dataset, which is

characterized in Section 4.1.

Topic-sensitive ranking strategies can directly be

applied to the task of searching for resources, e.g.

FolkRank-based algorithms can model the search

query within the preference vector (see Equation 1 in

Section 5.1.1) in order to compute a ranked search

result list. In (Abel et al., 2008b) we evidence that

our group-sensitive ranking algorithms like GFolk-

Rank (see Section 5.1.2) improve the search and rank-

ing quality signiﬁcantly (one-tailed t-test, signiﬁcance

level α = 0.05) compared to FolkRank. Non-topic-

sensitive ranking strategies – like SocialPageRank –

compute global, static rankings and therewith need a

baseline search algorithm, which delivers a base set

of possibly relevant resources, which serve as input

for the ranking algorithm. In our search experiments

we formulate the task to be performed by the ranking

strategies as follows.

Search Task. Given a base set of possibly relevant

resources, the task of the ranking algorithm is to

put these resources into an order so that the most

relevant resources appear at the very top of the

ranking.

6.1 Metrics and Test Set

For evaluating the quality of the ranking strategies

with respect to the search task we utilized the OSim

and KSim metrics as proposed in (Haveliwala, 2003).

OSim(τ

,τ

) enables us to determine the overlap be-

tween the top k resources of two rankings, τ

and τ

OSim(τ

,τ

) =

∩ R

, (3)

where R

⊂

R are the sets of resources that are

contained in the top k of ranking τ

and τ

respec-

tively, and |R

| = |R

| = k.

KSim(τ

,τ

) indicates the degree of pairwise dis-

tinct resources, r

and r

, within the top k that have

the same relative order in both rankings.

KSim(τ

,τ

) =

|{(r

):τ

,τ

agree on order of (r

),r

6=r

∪τ

|∗(|R

∪τ

|−1)

(4)

∪τ

is the union of resources of both top k rank-

ings. When detecting whether both rankings agree on

the order of two resources, we use τ

and τ

. τ

corre-

sponds to ranking τ

extended with resources R

that

are contained in the top k of τ

and not contained in

. We do not make any statements about the order of

resources r ∈ R

within ranking τ

. τ

is constructed

correspondingly.

In our analysis we apply OSim and KSim in order

to compare rankings computed by the ranking strate-

gies with optimal rankings. The optimal rankings are

based on 50 hand-selected rankings: Given 10 key-

words, which were out of the set of tags T , 5 experts

independently created rankings for each of the key-

words, which represented from their perspective the

most precise top 20 ranking of resources. Therefore,

they were enabled to inspect and the entire GroupMe!

dataset. By building the average ranking for each key-

word, we gained 10 optimal rankings. Among the 10

keywords, there are frequently used tags as well as

seldom used ones.

6.2 Base Set Detection

The base set contains all search results, which are ﬁ-

nally returned as a search result list, where the order

is computed by the ranking algorithm. Hence, it is

important to have a search method, which produces

WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies

172

a base set containing a high number of relevant re-

sources (high recall) without loosing precision. Table

2 compares different base set detection methods with

each other.

Table 2: Comparison of different procedures to determine

the basic set of relevant resources. Values are measured

with respect to the test set described in Section 6.1.

Base Set Algorithm Recall Precision F-measure

Basic 0.2767 0.9659 0.4301

BasicG 0.5165 0.7815 0.6220

BasicG

0.8853 0.6120 0.7237

Basic Returns only those resources, which are di-

rectly annotated with the search keyword (cf.

in Deﬁnition 6).

BasicG Returns in addition to Basic also resources,

that are contained in groups annotated with the

query keyword (cf.

∪

in Deﬁnition 6).

BasicG

This approach exploits group structures

more extensively. It corresponds to our GRank

algorithm without ranking the resources (cf.

Deﬁnition 6).

Having a recall of nearly 90%, BasicG

clearly

outperforms the other approaches. Though the pre-

cision is lower compared to Basic, which searches

for directly annotated resources, the F-measure – the

weighted mean of precision and recall – certiﬁes the

decisive superiority of BasicG

. In our experiments

we thus utilize the group-sensitive BasicG

in or-

der to discover the set of relevant resources to be

ranked. All ranking algorithms therewith beneﬁt from

the power of BasicG

6.3 Experiment

In our experiment we proceed as follows. For each

keyword query of our test set described in Section 6.1

and each ranking strategy presented in Section 5.1 and

5.2 we perform three steps.

1. Identiﬁcation of the base set of possibly relevant

resources by applying BasicG

(see Section 6.2).

2. Execution of ranking algorithm to rank resources

contained in the base set according to their rele-

vance to the query.

3. Comparison of computed ranking with the opti-

mal ranking of the test set by measuring OSim and

KSim (see Section 6.1).

Finally, we average the OSim/Ksim values for

each ranking strategy.

6.4 Results

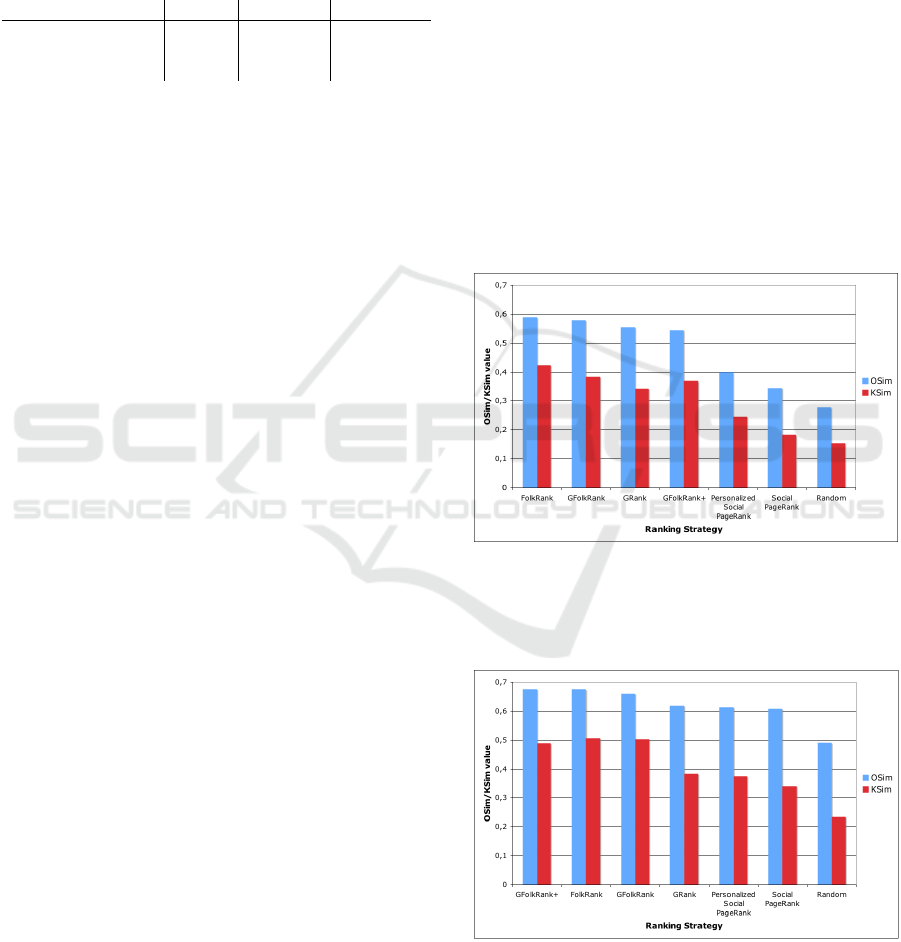
Figures 4 and 5 present the results we obtained by run-

ning the experiments as described in the previous sec-

tion. On average, the base set contains 58.9 resources

and the average recall is 0.88 (cf. Table 2). The ab-

solute OSim/KSim values are therewith inﬂuenced by

the base set detection. For example, regarding the Top

20 results in Table 5, the best possible OSim value

achievable by the ranking strategies is 0.92, whereas

the worst possible value is 0.27, which is caused by

the size and high precision of the base set. OSim and

KSim both do not make any assertions about the rel-

evance of the resources contained in the Top k. They

measure the overlap of the top k rankings and the rel-

ative order of the ranked resources, respectively (see

Section 6.1).

As expected, the strategy, which ranks resources

randomly performs worse. However, due to the high

Figure 4: Top 10 OSim/KSim comparison between different

ranking strategies. Basic Set is determined via BasicG

(cf.

Section 6.2). Best possible OSim: 0.95. Worst possible

OSim: 0.04.

Figure 5: Top 20 OSim/KSim comparison between different

ranking strategies. Basic Set is determined via BasicG

(cf.

Section 6.2). Best possible OSim: 0.92. Worst possible

OSim: 0.27.

CONTEXT-AWARE RANKING ALGORITHMS IN FOLKSONOMIES

173

quality of the group-sensitive base set detection al-

gorithm, the performance of the random strategy is

still acceptable. SocialPageRank is outperformed

by the topic-sensitive ranking algorithms. Person-

alized SocialPageRank, the topic-sensitive version,

which we developed in Section 5.2.2, improves the

OSim-performance of SocialPageRank by 16% and

the KSim-performance by 35%, regarding the top 10

evaluations.

The FolkRank-based strategies perform best, es-

pecially when analyzing the measured KSim values.

Regarding the performance of SocialPageRank within

the scope of the top 10 analysis, FolkRank, GFolk-

Rank, and GFolkRank

improve KSim by 132%,

110%, and 102% respectively. Here, the results

evaluated by the OSim metrics also indicate an in-

crease of the ranking quality, ranging from 58% to

71%. The GRank algorithm can compete with the

FolkRank-based algorithms and produces – with re-

spect to OSim and KSim – high quality rankings

as well. For example in our top 10 evaluations,

GRank performs 65%/89% (OSim/KSim) better than

SocialPageRank, whereas FolkRank improves GRank

slightly by 5%/25% (OSim/KSim). The promising

results of GRank are pleasing particularly because

GRank does not require computationally intensive

and time-consuming matrix operations as required by

the other ranking algorithms.

The group-sensitive ranking strategies do not im-

prove the ranking quality signiﬁcantly. However, all

ranking algorithms listed in Figures 4 and 5 beneﬁt

from the group-sensitive search algorithm, which de-

termines the basic set and which supplies the best (re-

garding F-measure) set of resources that are relevant

to the given query.

7 CONCLUSIONS

Folksonomy systems are valuable sources for improv-

ing search for Web resources. In this paper, we have

described, proposed, and extended different graph-

based ranking strategies for folksonomy systems, and

evaluated and compared their performances with re-

spect to ranking of search results. In addition, we

analyzed the effect of using additional information

about the context, in which some tagging activity took

place, namely the group context provided by social

systems like GroupMe!, on search and ranking. Our

evaluations show that by exploiting group context we

improve search performance in terms of both, recall

as well as overall quality (measured via F-measure).

The discussed graph-based ranking strategies overall

perform very well in ranking search results. They

have in common that they all adapt in one way or the

other the PageRank (Page et al., 1998) ideas. How-

ever, those strategies which utilize the full folkson-

omy information and are topic-sensitive perform best.

REFERENCES

Abel, F., Frank, M., Henze, N., Krause, D., Plappert, D.,

and Siehndel, P. (2007). GroupMe! – Where Semantic

Web meets Web 2.0. In Int. Semantic Web Conference

(ISWC 2007).

Abel, F., Henze, N., and Krause, D. (2008a). Exploiting

additional Context for Graph-based Tag Recommen-

dations in Folksonomy Systems. In Int. Conf. on Web

Intelligence and Intelligent Agent Technology (WI-IAT

2008). ACM Press.

Abel, F., Henze, N., Krause, D., and Kriesell, M. (2008b).

On the effect of group structures on ranking strategies

in folksonomies. In Workshop on Social Web Search

and Mining at 17th Int. World Wide Web Conference

(WWW ’08).

Bao, S., Xue, G., Wu, X., Yu, Y., Fei, B., and Su, Z. (2007).

Optimizing Web Search using Social Annotations. In

Proc. of 16th Int. World Wide Web Conference (WWW

’07), pages 501–510. ACM Press.

Haveliwala, T. H. (2003). Topic-Sensitive PageRank:

A Context-Sensitive Ranking Algorithm for Web

Search. IEEE Transactions on Knowledge and Data

Engineering, 15(4):784–796.

Hotho, A., J

aschke, R., Schmitz, C., and Stumme, G.

(2006a). BibSonomy: A Social Bookmark and Pub-

lication Sharing System. In Proc. First Conceptual

Structures Tool Interoperability Workshop, pages 87–

102, Aalborg.

Hotho, A., J

aschke, R., Schmitz, C., and Stumme, G.

(2006b). FolkRank: A Ranking Algorithm for Folk-

sonomies. In Proc. of Workshop on Information Re-

trieval (FGIR), Germany.

Li, X., Guo, L., and Zhao, Y. E. (2008). Tag-based social

interest discovery. In Proc. of the 17th Int. World Wide

Web Conference (WWW’08), pages 675–684. ACM

Press.

Marlow, C., Naaman, M., Boyd, D., and Davis, M. (2006).

HT06, tagging paper, taxonomy, ﬂickr, academic arti-

cle, to read. In Proc. of the 17th Conf. on Hypertext

and Hypermedia, pages 31–40. ACM Press.

Vander Wal, T. (2007). Folksonomy.

http://vanderwal.net/folksonomy.html.

Page, L., Brin, S., Motwani, R., and Winograd, T. (1998).

The PageRank Citation Ranking: Bringing Order to

the Web. Technical report, Stanford Digital Library

Technologies Project.

Sigurbj

ornsson, B. and van Zwol, R. (2008). Flickr tag rec-

ommendation based on collective knowledge. In Proc.

of 17th Int. World Wide Web Conference (WWW ’08),

pages 327–336. ACM Press.

WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies

174