TOWARDS AUTOMATED MANAGEMENT

OF COMPILER ASSIGNMENTS

Leena Salmela, Jorma Tarhio and Timo Montonen

Department of Computer Science and Engineering, Helsinki University of Technology, P.O.Box 5400, FI-02015 TKK, Finland

Keywords:

Courseware, Computer science, Compiler assignments.

Abstract:

We have implemented two software systems for managing compiler assignments in computer science. The ﬁrst

system is a graphical environment on the Web for doing home assignments related to ﬁnite state automata and

parsers. It also includes an automatic assessment system for the assignments. The second system manages

compiler projects. It generates a personalized language for each student and provides a testing tool for the

student’s compiler. We introduce the main features of the systems and review some experiences.

1 INTRODUCTION

We consider the application of information technolo-

gies in teaching a computer science course on com-

piling of programming languages. Such a course be-

longs to the computer science curriculum of many

universities. Recently we reorganized our compiler

course. We used to have one graduate course, which

has now been split into two courses. The ﬁrst one is

an introductory course for undergraduate students. It

deals mainly with the front-end of a compiler. The

second course is for graduate students. It covers ad-

vanced topics on the back-endbeyond the scope of the

original course. The change also created an opportu-

nity to reorganize the assignments of the ﬁrst course.

We use home assignments in our course. In our

former system, a teaching assistant graded the writ-

ten answers submitted by the students. Several prob-

lems arose with this approach. First of all, with our

resources it was not possible to give individual feed-

back to one hundred students, and the delay of the

feedback was two weeks, which was too long. Pla-

giarism has also been a growing concern in the course

since all students had the same assignments. Some

students also found the previous practice of returning

the home assignments as text ﬁles in a speciﬁed form

unintuitive.

To attack these problems we automated the home

assignments. Automatic assessment allows immedi-

ate feedback to the students and it is possible to give

individual assignments to students thus alleviating the

problem of plagiarism. Our system is called ACE

which is short for Automated Compiler Exercises.

ACE works on the Web. The preliminary version of

ACE was introduced in the work-in-the-progress pa-

per (Salmela and Tarhio, 2004). Here we deal with the

production version, which has been used four times.

The main features of ACE are explained in Section 2.

In Section 4 we review some experiences of ACE.

Besides home assignments, there is an obliga-

tory project in the course. In our former graduate

course, students worked in pairs and implemented

a small compiler with register allocation mostly by

hand. The assignment was the same for all students.

Because the project of an undergraduate course can-

not be equally demanding, we dropped register allo-

cation and other advanced features and shifted to ex-

tensive use of a compiler writing system. In order to

decrease the workload of the teaching assistant, we

implemented a tool called TKKCC for managing the

projects. TKKCC is short for TKK

Compiler Con-

struction. Because TKKCC is able to generate a per-

sonalized language for each student, it was natural to

shift to individual assignments to alleviate plagiarism.

TKKCC also provides a testing tool for a student’s

compiler. So far TKKCC has been used only once in

our course. The details of TKKCC are introduced in

Section 3 and experiences are reviewed in Section 4.

The ofﬁcial abbreviation of Helsinki University of

Technology is TKK, which comes from the Finnish name

Teknillinen korkeakoulu.

243

Salmela L., Tarhio J. and Montonen T. (2009).

TOWARDS AUTOMATED MANAGEMENT OF COMPILER ASSIGNMENTS.

In Proceedings of the First International Conference on Computer Supported Education, pages 243-249

DOI: 10.5220/0001839602430249

 SciTePress

2 ACE

2.1 Background

ACE contains a Web-based graphical environment for

studying and completing the assignments. The visual-

izations are mostly adapted from JFLAP (Cavalcante

et al., 2004), which is a visualization tool for formal

languages and automata theory. JFLAP is based on

earlier work of Susan Rodger.

Automatic assessment has been successfully used

in introductory courses at our university (Malmi et

al., 2003). For example, the Ceilidh system (Ben-

ford et al., 1993) and Scheme-Robo (Saikkonen et al.,

2001) have been used in the programming courses,

the TRAKLA2 system (Korhonen et al., 2003), which

has a graphical interface for doing algorithm sim-

ulation exercises, has been used in the Data Struc-

tures and Algorithms course, and the Stratum frame-

work (Janhunen et al., 2004) has been used in several

courses in our university. Automatic assessment has

proved to be effective in these cases and the student

response has also been generally positive.

There are a number of tools visualizing at least

some parts of a compiler (Boroni et al., 2001; Cav-

alcante et al., 2004; Tscherter et al., 2002; Resler

and Deaver, 1998; Khuri and Sugano, 1998; Ker-

ren, 1999; Vegdahl, 2001). Several visualizations

of ﬁnite automata and parsers have been developed.

Some of these visualization tools, like JFLAP (Cav-

alcante et al., 2004) and Exorciser (Tscherter et al.,

2002), have taken a step towards automatic assess-

ment. They allow students to try building their own

solutions. When the student is ready, the tool will

assess the solution and tell the student if it is right.

These tools also allow the student to take a look at

the model answer. However, these tools do not fully

cover the assignments we have used and they are in-

tended for self study so that they do not keep track

of students’ points and solutions. Solution building

and verifying the solution are fully separated in ACE.

This makes it possible to embed ACE in a framework

supporting automatic assessment and grading.

2.2 Overview of the Assignments

The assignments of our undergraduate course have

been organized into three rounds. In our former grad-

uate course, they were the ﬁrst three rounds out of six.

They deal with ﬁnite state automata (FSAs), LL pars-

ing, and LR parsing, respectively. The FSA round has

four assignments and the other rounds have ﬁve as-

signments.

In the ﬁrst assignment of the FSA round the stu-

dent is given a regular expression and the task is to

form a nondeterministic ﬁnite state automaton (NFA)

using Thompson’s construction. Then in the second

assignment the constructed NFA is simulated with a

given input. In the third assignment the NFA is con-

verted to a deterministic ﬁnite state automaton (DFA)

and this DFA is then simulated in the last assignment

of this round.

The second round deals with LL parsing. First

the student should remove left recursion from a given

grammar. In the second assignment this grammar is

left factored. Then in the third assignment the First

and Follow sets needed in the LL parse table con-

struction are calculated. The parse table is ﬁlled and

in the last assignment the constructed parser is simu-

lated with a given input.

In the third round an LR parser is constructed. In

the ﬁrst assignment the student forms the LR(0) item

sets of a given grammar and ﬁgures out the transi-

tions between them. Then in the second assignment

the First and Follow sets are calculated. Based on

these sets also the LR parse table is constructed. The

grammar used in this assignment is ambiguous so the

parse table now contains ambiguity. In the fourth as-

signment of this round the ambiguity is removedfrom

the parse table so that given precedence and associa-

tivity constraints are satisﬁed. In the last assignment

the constructed parser is simulated with a given input.

Some of these assignments are clearly algorithm

simulation exercises. The simulation of an FSA or

a parser clearly falls into this category. The solution

to this kind of assignment is an ordered list of steps.

Some of the other assignments include simulation of

an algorithm but the algorithm is more loosely de-

ﬁned. For example, the Thompson’s construction al-

gorithm does not deﬁne a total order for the construc-

tion of the automaton parts. Thus it only deﬁnes a

partial order for the steps that are needed to construct

the whole automaton. Of course a total order may be

enforced in such an algorithm but this would unneces-

sarily complicate the assignment. Some of the assign-

ments are even more loosely deﬁned like the removal

of left recursion from a grammar. In this case some

transformation rules are presented in the study mate-

rial but the use of exactly these rules is not enforced.

These assignments are conceptual in nature. They test

the student’s understanding of the concept rather than

knowledge of a speciﬁc algorithm.

We have ten assignment sets for the ﬁrst round and

nine assignment sets for the last two rounds. Assign-

ments for each student are chosen randomly among

those sets. Moreover we allow permuting and replac-

ing of local strings and names in the assignments in

CSEDU 2009 - International Conference on Computer Supported Education

244

order to artiﬁcially increase the number of different

assignments. We are also studying ways to gener-

ate new grammars and regular expressions for assign-

ments.

2.3 Implementation

Architecture. Given the various types of assign-

ments that the system needs to support, we decided

to build a client for the students to do the assignments

in a computer-aided manner and veriﬁers for check-

ing them. These components can then be embedded

into a frameworkwhich takes care of submissions and

the needed book keeping. We call the client with the

veriﬁers ACE.

Overviews of the client and the veriﬁers are given

below. We have embedded the client and the veri-

ﬁers in the Stratum framework (Janhunen et al., 2004)

which follows the client/server architecture. Records

on assignments, submissions, and results are kept on

the server.

Stratum provides a personal Web page for each

student. The ACE client is embedded as an applet

to this Web page. This applet is the graphical envi-

ronment for doing the assignments and the student

also submits the solutions with the applet. The per-

sonal Web page of the student also shows personal

assignments of the student and the submission status

of each subtask. The veriﬁers module is embedded in

the server.

ACE Client. The central part of the ACE client is

the visualization of the data structures needed in the

assignments. Most of these features are present in

JFLAP (Cavalcante et al., 2004). Thus the ACE client

was built reusing the code from JFLAP. However,

some changes also needed to be done. JFLAP does

not support showing precedence and associativity in-

formation of operators, and so visualization for this

was built. The simulation of FSAs and parsers in

JFLAP are merely animations, and thus we needed

to add some interaction so that the students can show

how an FSA or parser works. For example, when sim-

ulating an LL parser the student has two choices in

each step: to advance in the input or to apply a rule

from the parse table.

Another major change was adding the notion of

assignment rounds and assignments. Now ACE can

lead the student through an assignment round one as-

signment at a time. Other changes included the design

of a new ﬁle format which contains the information

about assignments and assignment rounds. Because

of the new ﬁle format it is also not so easy for the stu-

dents to use JFLAP to generate the correct answers.

The generation of correct answers was of course dis-

abled from the user interface.

Fig. 1 shows a screenshot of the ACE client. Here

a NFA is being converted to a DFA. The student has

already deﬁned the initial state of the DFA and the

state which the DFA enters after reading the symbol

’x’ in the initial state. The labels of the DFA states

show their corresponding NFA state sets.

Veriﬁers. We were also able to reuse some parts of

JFLAP when building the veriﬁers. Some of the as-

signments like removing left recursion from a gram-

mar are not supported by JFLAP so we needed to im-

plement new veriﬁers for these. The simulation of

FSAs and parsers in JFLAP are only animations with-

out the possibility of error so we needed to implement

new veriﬁers for these too.

The veriﬁers have the following general structure.

First they check if the input the student used was the

one given in the assignment. Then they check if the

student’s solution is correct and generate feedback to

the student. Most of the veriﬁers check the student’s

solution by generating a model answer and compar-

ing that to the student’s solution. However, in some

cases this process does not provide a way to generate

good feedback to the student and thus the solution is

checked in a different manner.

For example, the ﬁrst assignment of the FSA

round is checked by reversing Thompson’s construc-

tion and comparing the regular expressions. This way

we are better able to tell the student which part of the

automaton is correct and which part could not have

been generated by Thompson’s construction or is gen-

erated for a wrong regular expression.

Also the assignments, where left recursion is re-

moved from a grammar or a grammar is left fac-

tored, are checked somewhatdifferently. First the ver-

iﬁer checks that the undesirable elements have been

removed from the grammar and then it checks that

the new grammar produces the same language as the

original one. Note that it is intractable to check if

two context free grammars produce the same lan-

guage but in our case the problem is decidable if we

assure that both of the grammars are LL(k) gram-

mars (Rosenkrantz and Stearns, 1970; Olshansky and

Pnueli, 1977).

3 TKKCC

Our compiler course has a mandatory project. Each

student is given a small language, and the goal of the

project is to implement a compiler for it. The student

builds a compiler with the Java version of the Coco/R

TOWARDS AUTOMATED MANAGEMENT OF COMPILER ASSIGNMENTS

245

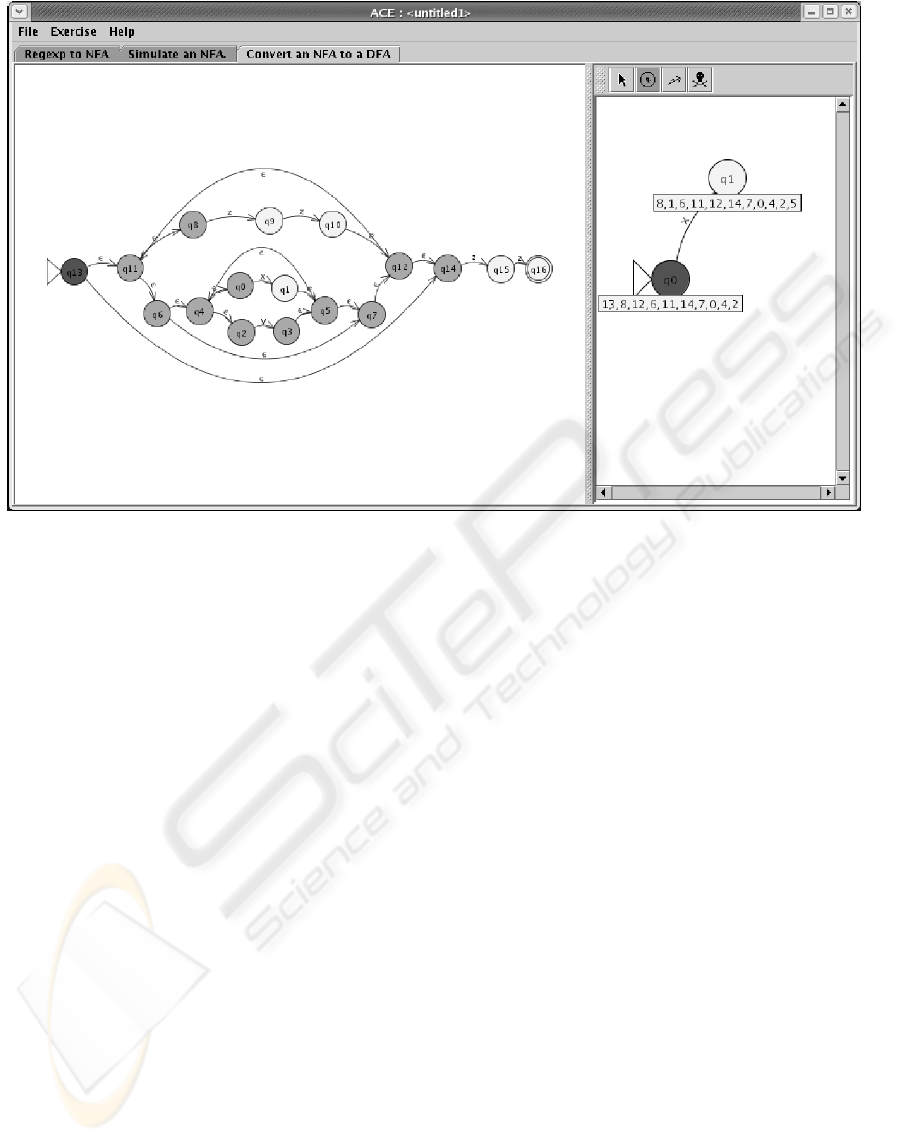
Figure 1: A screenshot from the ACE client. Here the user is converting a NFA to a DFA.

compiler generator (M¨ossenb¨ock et al., 2008). The

compiler should generate code for a virtual stack ma-

chine so that the code could be executed with a given

interpreter. The student’s task is to write an attribute

grammar with a few Java classes for the language.

The attribute grammar includes code generation.

We implemented a support system called TKKCC

for managing projects of our course. TKKCC has

three parts:

• Language generator creates automatically a per-

sonalized language for each student. We designed

a base language called Consensus. In generation,

a set of its features is selected to the student’s lan-

guage.

• Test generator prepares tests for the student’s

language. We have a large collection of hand-

made test programs for Consensus, and the test

generator translates these programs to the stu-

dent’s language. Expected output is associated

with each test program.

• Test driver uses the student’s compiler to com-

pile test programs and then executes the generated

code. The test driver then shows the real output

and the expected one. Because the test driver ex-

ecutes code written by students, we have used the

Java security manager to restrict access to the sys-

tem.

As in the case of ACE, we use the Stratum frame-

work (Janhunen et al., 2004) to manage the submis-

sions and keep track of the different assignments of

students. The Stratum framework calls the language

generator and test generator when the project assign-

ment is created for the students. The students can then

access their assignment and related test ﬁles and sub-

mit the project on the Web. When the student submits

a project, Stratum then calls the test drivers to auto-

matically run the tests. The teaching assistant can

then use the tools provided by Stratum to check on

the progress of the students.

The Consensus language has integer and Boolean

data types and integer arrays. Control structures in-

clude the if statement and the loop structure. Con-

sensus has functions with parameters. The student’s

language is a subset of Consensus with syntactic vari-

ation. Each element of Consensus has several syn-

tactic alternatives. For example, Consensus has four

forms of the loop structure:

• do Statement while (Expression)

• repeat Statement until (Expression)

• while (Expression) do Statement

• for (Statement; Expression; Statement) Statement

In a way, the interpreter of the target code is a part

of TKKCC, because it has been integrated with the

test driver. However, the interpreter naturally depends

on the target code used.

CSEDU 2009 - International Conference on Computer Supported Education

246

The language generator was implemented with

templates of the FreeMarker library (FreeMarker,

2008). The language is given to the student as a

context-free grammar. The test driver was imple-

mented with Groovy (Groovy, 2008), which is a ﬂex-

ible script language.

Related Systems. There are a few earlier sys-

tems that are related to the principles of TKKCC.

VCOCO (Resler and Deaver, 1998) is another in-

structional tool developed for Coco/R but its objec-

tive is different from TKKCC. VCOCO visualizes

LL(1) parsers generated by the C version of Coco/R.

VCOCO shows corresponding parts in the grammar,

generated code, and input. Unfortunately, VCOCO

does not work with the Java version of Coco/R and

thus could not be used in our course. Otherwise it

would have been useful for our students.

ART (Aycock, 2003) is a tool which helps to cre-

ate more complex test programs for compilers writ-

ten as course projects. In this kind of projects the

compiled language is often a simple toy language

which lacks more complex structures like arrays. This

makes it difﬁcult to construct complex programs suit-

able for stress testing students’ compilers. ART gen-

erates such complex input programs by translating

arrays of ﬁxed size to single variables and replac-

ing array references by references to the variable cor-

responding to that item. ART could be used with

TKKCC to create more complex test programs. How-

ever, because the Consensus language of TKKCC has

arrays, it is not so tedious to create complex test pro-

grams.

Cool (Aiken, 1996) is a support system for com-

piler projects. Cool provides a portable compiler

project, a class library, which contains common rou-

tines of a compiler, a reference compiler and a lan-

guage reference manual for the input language of the

compiler project. Cool has modular assignments that

have been designed to be independent and thus a stu-

dent is able to continue the project even if an earlier

phase has failed.

4 EXPERIENCES

4.1 ACE

The main advantage of ACE is the signiﬁcant de-

crease in the workload of the teaching assistant, be-

cause ACE delivers and assesses the assignments as

well as gives feedback to the students. The time

needed for yearly maintaining is short.

There are three assignment rounds (involved with

the front-end of the compiler) in the course. In order

to pass the course students have to pass two of these

rounds. Doing more than the required number of as-

signments is voluntary and does not give any extra

credit to the students. After adopting ACE the per-

centage of students who completed all three rounds

increased from 37% to 51% (the ﬁgures are averages

over several years).

When ACE was used for the ﬁrst time, we asked

the students of the course to answer a questionnaire,

and 60% of the 91 students replied. Concerning the

possible advantages of ACE, the most common an-

swer dealt with immediate feedback, which helped

students to correct their mistakes. Also the ability to

make a round incrementally in several sessions and

the possibility to iterate answers were important ben-

eﬁts.

Several students said that ACE saves time when

compared with the traditional pen and paper way.

However, the students who already mastered the

topic of an assignment before using ACE found the

computer-aided approach slower than pen and paper,

because learning ACE was in a way additional to

them. Related to this, we asked whether the students

felt wasting time with ACE. Only 13% of them an-

swered yes, and 2% were uncertain. The rest 85% did

not waste time. The average use time per round was 4

h 8 min.

We also asked the students if they encountered

any problems when using ACE, and 76% of them re-

ported some problems, mostly minor technical prob-

lems. All the problems have already been corrected.

A typical complaint dealt with vague error messages

and unclear and limited instructions. Several students

wished for demonstrations and examples in order to

get easier acquainted with the system.

Then we asked whether ACE supported learning.

The answer was clear: 96% of the students answered

“yes”.

We requested the students to compare ACE with

similar computer-aided tools for homework assign-

ments of other courses. There are at least three other

courses using such technology at our department. So

80% of the students had used similar systems earlier.

ACE was well received, and almost half of students

considered it to be at least better than the other sys-

tems. One student explained his opinion as follows

pointing out some problems of computer-aided in-

struction: “ACE is better because it is not as mechan-

ical as some other tools, which do not require ponder-

ing at all; yet even ACE provides so much help (in

guiding towards the solution) that if only using ACE,

one does not know what to do without it. So ACE is

TOWARDS AUTOMATED MANAGEMENT OF COMPILER ASSIGNMENTS

247

good, but pen-and-paper is still needed.”

Among the same student group we made another

questionnaire in connection with the course evalua-

tion in which 54% of the students participated. A

course evaluation is organized in the end of every

course at our department. Besides ﬁxed questions,

the teacher is allowed to present additional questions.

We asked the students to compare ACE with the tra-

ditional approach. The group studied the original ver-

sion of our course so that they had also three other

assignment rounds concerning the back-end of a com-

piler. These rounds consisted of traditional pen-and-

paper assignments. The ﬁrst questionnaire took place

in the middle of the course, whereas the students had

completed all the assignments while the second ques-

tionnaire was made.

The ﬁrst question dealt with meaningfulness.

Only few of the students had experienced the tradi-

tional way more meaningful than ACE. One third did

not see any difference between the alternatives, and

more than half found the computer-aided way more

meaningful.

Next the students were asked to compare the labo-

riousness of the approaches. Based on the ﬁrst ques-

tionnaire we already knew that those students, who

already mastered the subject, wasted time whereas

those students, who did not know the subject before-

hand, saved time. Now in the end of the course, half

of the students found the traditional way more labo-

rious. About one third experienced both approaches

similar, and the rest of the students considered ACE

more laborious.

The last question was about learning. Half of

the students thought that the computer-aidedapproach

was better from the point of view of learning. Only

12% of them found the traditional approach better.

The summary of the second questionnaire is given in

Table 1.

Table 1: Answers to the question: Which way was more

meaningful, more laborious, and better from the point of

view of learning? ACE or the traditional approach? The

numbers are percentages.

Which way was... ACE No diff. Trad.

More meaningful? 59 33 8

More laborious? 18 31 51

Better from the point

of view of learning? 51 37 12

4.2 TKKCC

TKKCC saves the teaching assistant’s time but not at

all as much as in the case of ACE. TKKCC delivers

the assignments automatically. Many students need

consulting, and TKKCC cannot help much. It only

provides semi-automatic assessment as it only runs

tests automatically but the teaching assistant will still

have to check other issues like documentation.

From the student’s point of view, TKKCC does

not offer much additional when compared with con-

ventional use of Coco/R. However, the testing capa-

bility is a new service and the students also appreci-

ated this feature.

5 CONCLUDING REMARKS

We have described two systems managing compiler

assignments. The ACE system automatically as-

sesses assignments related to ﬁnite state automata and

parsers. The system supports individual assignments

for students and it has a visual interface for study-

ing and completing the assignments. The system has

been used four times in our compiler course, and it

was well received by the students.

ACE is an advanced learning environment. It

makes the concepts of compiler construction concrete

by visualizing them. ACE supports learning by do-

ing. The student can submit a trial solution, and the

system gives feedback about the possible errors. Be-

cause only correct submissions are accepted, the stu-

dent is allowed to try each assignment of a round sev-

eral times. Most of the assignments are constructed

in such a way that it is almost impossible to reach an

acceptable solution only by guessing.

ACE shares a part of the visualizations of JFLAP

which is an excellent tool for demonstration and self-

study purposes. However, the integrated assessment

and bookkeeping make ACE more useful than JFLAP

because the assignments of a large course can be de-

livered and graded automatically with ACE.

ACE works on the Web so that students can do the

assignments anywhere at the time suitable for them.

Thus ACE suits well to distance learning e.g. in a vir-

tual university. The general principles of ACE can

be adapted to other subjects with constructive assign-

ments.

TKKCC manages compiler projects. It generates

languages for students, and provides a testing frame-

work for the implemented compiler. We plan to add

a new module, which would help students in writ-

ing attribute grammars for Coco/R, to TKKCC . This

module would recognize some typical errors students

make and provide instructions on how to proceed.

Recently we have updated the language generator

of TKKCC so that it produces two alternative assign-

ments for each student: easy and full. Arrays, and

functions and function calls have been removed from

CSEDU 2009 - International Conference on Computer Supported Education

248

the easy assignment and the associativity and prece-

dence of operators in expressions have been solved

for the student in a trivial way by requiring explicit

use of parenthesis in the input programs of the stu-

dent’s compiler. This will allow the weaker students

to start working with an easy assignment while still

giving them the possibility to switch to the full as-

signment later. Of course, the highest points cannot

be scored with an easy assignment. This feature will

be used in our course this fall for the ﬁrst time.

Both of the tools, ACE and TKKCC, are freely

available.

ACKNOWLEDGEMENTS

We thank Susan Rodger and Tomi Janhunen for let-

ting us use their codes. The help of Venla Hyt¨onen is

appreciated.

REFERENCES

Aiken, A. (1996). Cool: a portable project for teaching com-

piler construction. SIGPLAN Not. 31(7):19–24.

Aycock, J. (2003). The art of compiler construction

projects. SIGPLAN Not. 38(12):28–32.

Benford, S., Burke, E., Foxley, E., Gutteridge, N., and Zin,

A. M. (1993). Ceilidh: A course administration and

marking system. In Proceedings of the 1st Interna-

tional Conference of Computer Based Learning.

Boroni, C., Goosey, F., Grinder, M., and Ross R. (2001).

Engaging students with active learning resources: Hy-

pertextbooks for the web. In Proceedings of the 32nd

SIGCSE Technical Symposium on Computer Science

Education, pages 65–69. ACM.

Cavalcante, R., Finley, T., and Rodger, S. H. (2004). A

visual and interactive automata theory course with

JFLAP 4.0. In Proceedings of the 35th SIGCSE Tech-

nical Symposium on Computer Science Education,

pages 140–144. ACM.

FreeMarker (2008). http://www.freemarker.org/. Oct. 2008.

Groovy (2008). http://groovy.codehaus.org. Oct. 2008.

Janhunen, T., Jussila, T., J¨arvisalo, M., and Oikarinen,

E. (2004). Teaching Smullyan’s analytic tableaux in

a scalable learning environment. In Proceedings of

the 4th Finnish/Baltic Sea Conference on Computer

Science Education.

Kerren, A. (1999). Animation of the semantical analysis.

In Proceedings of 8. GI-Fachtagung Informatik und

Schule, INFOS99. Informatik aktuell, Springer. (in

German).

Khuri, S. and Sugano, Y. (1998). Animating parsing algo-

rithms. In Proceedings of the 29th SIGCSE Technical

Symposium, pages 232–236. ACM.

Korhonen, A., Malmi, L., and Silvasti, P. (2003).

TRAKLA2: a framework for automatically assessed

visual algorithm simulation exercises. In Proceedings

of the 3rd Finnish/Baltic Sea Conference on Computer

Science Education, pages 48–56.

Malmi, L., Korhonen, A., and Saikkonen. R. (2002). Expe-

riences in automatic assessment on mass courses and

issues for designing virtual courses. In Proceedings of

the 7th Annual SIGCSE/SIGCUE Conference on In-

novation and Technology in Computer Science Edu-

cation, pages 55–59. ACM.

M¨ossenb¨ock, H., L¨oberbauer, M., and W¨oß, A. (2008).

The Compiler Generator Coco/R. http://www.ssw.uni-

linz.ac.at/coco/. Oct. 2008.

Olshansky, T. and Pnueli, A. (1977). A direct algorithm for

checking equivalence of LL(k) grammars. Theoretical

Computer Science 4:321–349.

Resler R. D. and Deaver, D. M. (1998). VCOCO: A visu-

alisation tool for teaching compilers. ACM SIGCSE

Bulletin, 30(3):199–202.

Rosenkrantz, D. J. and Stearns, R. E. (1970). Properties of

deterministic top-down grammars. Information and

Control, 17(3):226–256.

Saikkonen, R. , Malmi, L. , and Korhonen, A. (2001). Fully

automatic assessment of programming exercises. In

Proceedings of the 6th Annual SIGCSE/SIGCUE Con-

ference on Innovation and Technology in Computer

Science Education, pages 133–136. ACM.

Salmela, L. and Tarhio, J. (2004). ACE: Automated

compiler exercises. In Proceedings of the 4th

Finnish/Baltic Sea Conference on Computer Science

Education.

Tscherter, V., Lamprecht, R., and Nievergelt J. (2002). Ex-

orciser: Automatic generation and interactive grading

of exercises in the theory of computation. In 4th In-

ternational Conference on New Educational Environ-

ments, pages 47–50.

Vegdahl, S. R. (2001). Using visualization tools to teach

compiler design. Journal of Computing Sciences in

Colleges, 16(2):72–83.

TOWARDS AUTOMATED MANAGEMENT OF COMPILER ASSIGNMENTS

249