INCREMENTAL MAINTENANCE OF ONTOLOGIES BASED

ON BIPARTITE GRAPH MATCHING

Preetpal Singh and Kalpdrum Passi

Dept. of Math and Computer Science, Laurentian University, 935 Ramsey Lake Rd., Sudbury ON, Canada

Keywords: Semantic matching, Ontology structure, Ontology mapping, Data integration, Weighted bipartite graphs,

Max- weighted matching, Hungarian algorithm.

Abstract: Today’s Information Society demands complete access to available information, which is often

heterogeneous and distributed. A key challenge in building the Semantic Web is integrating heterogeneous

data sources. This paper presents an incremental algorithm for maintaining integration in evolving

ontologies. For example, an increased number of smaller, task oriented ontologies, are emerging across the

Bioinformatics domain to represent domain knowledge; integrating these heterogeneous ontologies is

crucial for applications utilizing multiple ontologies. Most ontologies share a core of common knowledge

allowing them to communicate, but no single ontology contains complete domain knowledge. Recent papers

examined integrating ontologies using bipartite graph matching techniques. However, they do not address

the issue of incrementally maintaining the matching in evolving ontologies. In this paper we present an

incremental algorithm, OntoMaintain, which incrementally calculates the perfect matching among evolving

ontologies and simultaneously updates the labels of the concepts of ontologies. We show that our algorithm

has a complexity of O(n

) compared to complexity O(n

) of traditional matching algorithms. Experimental

results prove that our algorithm maintains the correctness of a ‘brute force method’ while significantly

reducing the time needed to find a perfect matching in evolving ontologies.

1 INTRODUCTION

Information today is dispersed in a variety of

disparate sources like public or proprietary

databases, books, journals, scientific publications

and national archives. A significant amount of this

data exists in heterogeneous format. Unfortunately

analysts and scientists are not able to identify and

exploit this information easily because of the variety

of semantics, interfaces and data formats used by the

underlying data sources (Reichhardt, 1999).

Semantic heterogeneity, also referred to as

conceptual heterogeneity and logical mismatch,

underlines the differences in modelling the same

domain of interest. Fundamental to resolving

semantic and organizational differences is the task of

matching ‘semantically heterogeneous data’.

Ontologies are an important paradigm for

managing the exponential growth of valuable data

generated by new technologies (Gruber, 1993).

Ontologies model the structure of data in terms of

classes and their attributes; they also represent the

semantics of data in the form of axioms, such as

inheritance relationships. These semantics explain

the relationship between structure and data in

different ontologies, to create a consistent integrated

ontology. However, existing integration approaches

(Mowbray and Zahavi, 1995), (Paolucci, et. al.,

2002), (Pinto and Martins, 2000) result in a static

ontology, which is hard to evolve as the core sub-

ontologies evolve and expand.

A primary task in designing a data integration

method is, establishing a mapping scheme between

the data sources; mappings represent semantics of

relationships and are used to create an integrated

ontology (Doan, et. al., 2002).

Our mapping scheme represents concepts of

ontology as vertices of a bipartite graph (Melnik, et.

al., 2002); it then invokes a bipartite graph matching

algorithm (Bellur and Kulkarni, 2007) to find a

perfect matching between these vertices.

Furthermore, we use the semantics of ontologies, to

create a coherent and consistent integrated ontology.

In this paper we propose an incremental

algorithm, OntoMaintain, based on the concept of

weighted bipartite graph matching. Our algorithm

incrementally computes the new perfect matching

444

Singh P. and Passi K.

INCREMENTAL MAINTENANCE OF ONTOLOGIES BASED ON BIPARTITE GRAPH MATCHING.

DOI: 10.5220/0001843904440449

In Proceedings of the Fifth International Conference on Web Information Systems and Technologies (WEBIST 2009), page

ISBN: 978-989-8111-81-4

between ontologies and updates the labels of vertices

as a new pair of vertices are added to the ontology.

Experimental results prove that our algorithm

maintains the accuracy of the “brute force” method

and significantly reduces the computation time in

finding the perfect matching of the extended

ontology O’. Our algorithm results in a time

complexity of

O(n

) compared to complexity O(n

) of

running the Hungarian algorithm (Kuhn, 1955).

2 RELATED WORK

In order to accommodate both semantic and

schematic differences between heterogeneous data

sources, it is crucial to integrate ontologies across

various knowledge domains such as anatomy, drug

and disease ontology in biomedical domains. A good

example is the Gene Ontology (GO). GO provides a

consistent description of genes in different

biological databases. Each term in GO has a unique

numerical identifier and a name; terms are further

assigned to an ontology like molecular function,

cellular component or biological process. Past

publications like OASIS (Song et. al., 2006) have

cited GO in their proposed matching system.

GO represents two forms of relationships: is_a

and part_of relationships. The is_a relationship

represents a simple class subclass relationship,

where A is_a B means that A is a subclass of B. The

part_of relation is slightly more complex; C part_of

D means that whenever C is present, it is always a

part of D, but C does not always have to be present.

An example would be nucleus part_of cell; nuclei

are always part of a cell, but not all cells have nuclei.

(Bellur and Kulkarni, 2007) propose an

improved version of semantic matchmaking

algorithm by (Paolucci, et al., 2002) to dynamically

discover and invoke a web service. They use the

Hungarian algorithm (Kuhn, 1955) to compute a

complete matching of a bipartite graph but minimize

the maximum weighted edge of graph to get an

optimal matching; this optimization criterion is

different from the Hungarian algorithm.

None of the works cited above discusses the

issue of maintaining mappings in evolving

ontologies; how to calculate a perfect matching

incrementally, every time new vertices are added to

the graph?

3 ONTOLOGY MAPPING

3.1 Similarity Measures

By comparing terms of ontologies, we first calculate

the similarity values between them, based on certain

metrics; each metric establishes a value based on

certain characteristics. Similarity values are in the

range [0, 1]. Larger the value, more similar the two

terms are.

Linguistic Similarity. Is based on term names. A

string match algorithm is used to match the names.

Definition Similarity. Certain terms in the ontology

database have definitions attached; a text

classification algorithm compares two definitions

and calculates a similarity value between two terms.

Structure Similarity. Neighbours of a term are

parents and children of the node; probability of a

term being similar to another is high if neighbours of

both terms are matched.

Based on the above three metrics, a similarity

chart is computed. If we have n similarity charts,

each of which has similarity values Sim

(a, b), i =

1..n, for any pair of elements (a, b); the overall

similarity for each pair (a, b) is calculated as:

Higher the weight w

more is its importance and

preference.

Table 1: Match according to similarity values.

Value Range Match

0.50 – 1.00 Exact

0.25 – 0.50 Subsumption

0.25 – 0.00 Conditional

3.2 The Gene Ontology

The Gene Ontology is a well known web based bio-

ontology; an open source of bioinformatics

knowledge. We will use two key GO ontologies;

cellular component and molecular function as

examples to explain how the Match conditions

mentioned in Table 1 are assigned.

The cellular component and molecular function

ontologies are each represented as a directed acylic

graph or DAG. Relationships between any two

concepts in a DAG are depicted by semantic edges.

INCREMENTAL MAINTENANCE OF ONTOLOGIES BASED ON BIPARTITE GRAPH MATCHING

445

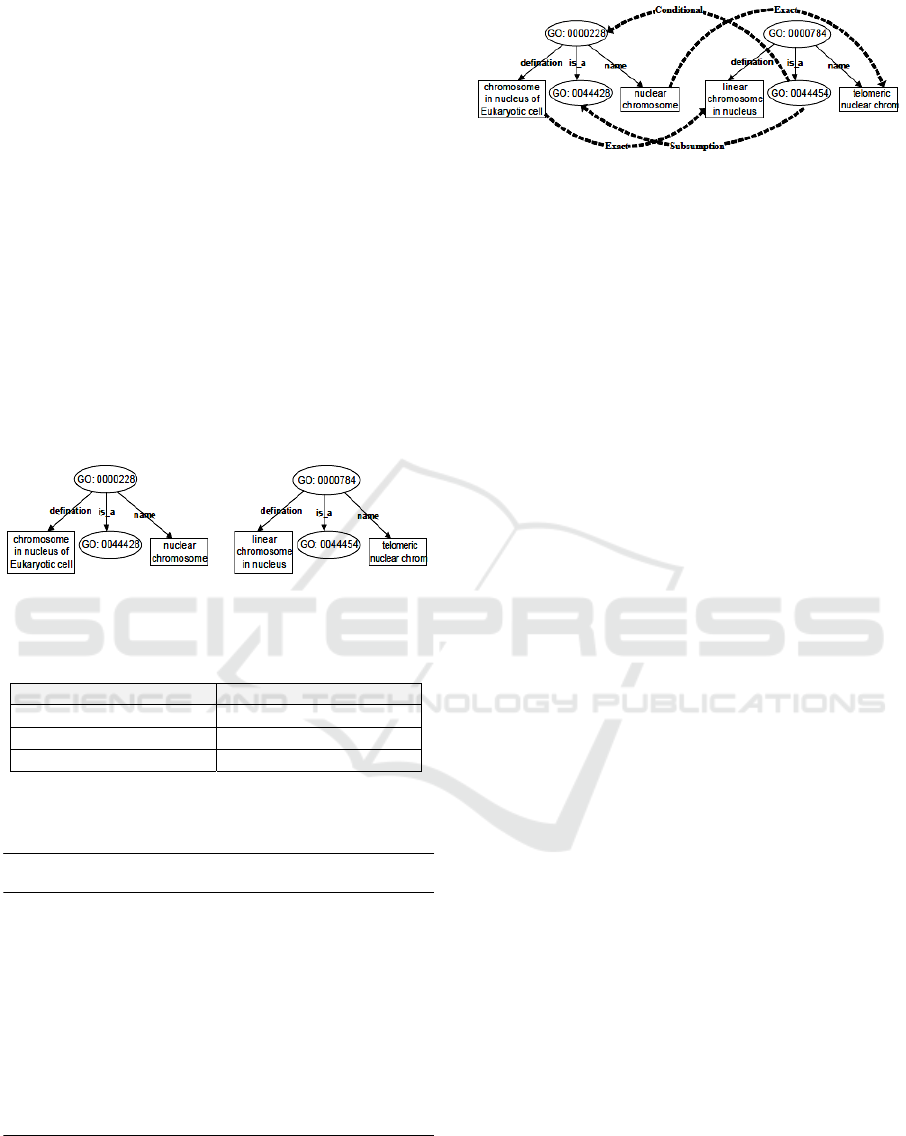
A gene may have more than one annotation in

different branches of GO. For example, the gene

nuclear chromosome is annotated as GO: 0000228

(Figure 1a) and GO: 0000784 (Figure 1b); it is

located in more than one cellular component, during

which it performs more than one molecular function.

Exact. Is the most desirable match. The degree exact

is assigned when a term in one ontology is

equivalent to or superclass of a term in another

ontology.

Subsumption. The degree subsumption is assigned

when a term of ontology includes a term in another

ontology i.e. it could be used as a substitute.

Conditional. The degree conditional is assigned

when a term of ontology doesn’t necessarily match a

term in the other ontology but may still be used to

achieve the desired result.

Figure 1a: Ontology O

. Figure 1b: Ontology O

Table 2: Weights according to degree of Match.

Match Weight

Exact w

Subsumption w

Conditional w

Exact > Subsume > Conditional

The criteria in Table 2 are implemented as follows:

Algorithm 1: match(value)

1: if value ≥ 0.50 then

2: return Exact

3: else if 0.50 ≤ value ≥ 0.25 then

4: return Subsume

5: else if value < 0.25 then

6: return Conditional

7: else

8: return Fail

9: end if

We match the concepts of ontologies O

and O

based on the matching criteria proposed in Table 1.

The final match is an integrated ontology O shown

in Figure 2 below.

Figure 2: Ontology O.

4 BIPARTITE GRAPH

MATCHING

4.1 Overview

A Bipartite Graph is a graph G = (V, E) in which the

vertex set can be partitioned into two disjoint sets,

V=V

U V

such that every edge e  E has one

vertex in V

and the other in V

A weighted bipartite graph G = (X U Y, X × Y)

having partitions with size V can be represented by a

weight matrix W of size V × V. In the weight matrix,

rows correspond to the X partition and columns

correspond to the Y partition of vertices. Each entry

represents the weight of the edge between the

vertices x

and y

Feasible vertex labelling l is defined on the

vertices of both partitions of the bipartite graph as

follows:

l (x

) + l(y

) ≥ w

 x

 X,  y

 Y

The subgraph corresponding to the feasible

vertex labeling l defined by the edges satisfying the

following equality is called the equality subgraph G

l (x

) + l(y

) = w

We seek the max-weighted perfect matching in

bipartite graphs.

5 INCREMENTAL ALGORITHM

Our algorithm is based on the Hungarian algorithm,

which produces the feasible vertex labelling of the

vertices together with the max-weighted matching.

OntoMaintain updates the new feasible vertex

labelling of the extended graph while producing the

max-weighted matching or so called perfect

matching.

The Hungarian algorithm assumes the existence

of a weighted bipartite graph, G = (X U Y, X × Y) as

described in Section 4.1. The edge weights, w

are

stored in a matrix W. An edge (x

, y

) is matched if x

is matched to y

and unmatched otherwise. We

WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies

446

represent matched edges with solid lines and

unmatched edges with dotted lines. Furthermore, let

S  X and T be neighbour of S i.e. T = nhbor(S) but

T ≠ Y. So T contains only those vertices from

partition Y, which are matched to a vertex in S.

The Hungarian algorithm outputs a complete

matching M*

The incremental algorithm adds a new pair of

vertices to the max-weighted matched bipartite

graph whose feasible vertex labelling is also given,

together with the max-weighted matching. Then, it

assigns any feasible labelling to the newly added

pair of vertices and, by using this labelling,

determines the maximum-weighted matching of the

whole extended bipartite graph.

When we add a new pair of vertices to the max-

weighted-matched graph, a new weight matrix is

generated by adding a new row and a new column to

the previous weight matrix as the (V + 1)st row and

column corresponding to the edges incident to the

new vertices.

Algorithm 2: OntoMaintain.

Input: The extended bipartite graph

G’= (X

U Y, X × Y), with partitions of size

V+1 represented by a weight matrix W’of size

(V + 1) × (V + 1)

A feasible vertex labeling l of the first V

vertices such that it corresponds to G

containing the max-weighted matching

among the first V vertices

The max-weighted matching M*

among

the first V vertices of the partitions

Output: Perfect matching M*

V+1

and the updated

labels l of the vertices of the extended

bipartite graph G’.

1. Begin with matching M*

derived by Hungarian

algorithm.

Assign labels to new vertices Y

V + 1

and X

V + 1

as follows:

l(Y

V+1

) = 0

l(X

V+1

)= max y

 Y (w

v+1

)

2. On the equality subgraph G

pick an unmatched

vertex in partition X (called U) using matching

. Grow a Hungarian tree rooted at this

vertex, while doing so; include all vertices

encountered in X (with U) into S and all vertices

encountered in Y into T.

3. If an augmenting path A is found, interchange

matched and unmatched edges in the augmenting

path. Calculate new matching by increasing size

by one.

4. If no augmenting path is found, revise the

labeling l. After label revision, labels of vertices

in S are decreased by the smallest possible

amount which adds at least one edge between S

and Y-T. Concurrently, labels of vertices in T are

increased by the same amount in order to

maintain the current matching between S and T.

Adding such edges will increase the chance of

finding an augmenting path. Revise labels as:

= min



S, yj



Y - T

{ l (x

) + l(y

) - w

}

l(v) + α

l’(v) =

l(v) - α

l(v) otherwise

5. Go to Step 2 to search for an augmenting path

with the new equality subgraph G’

defined by

the new labeling

5.1 Complexity Analysis

Our Incremental Algorithm, OntoMaintain, has a

time complexity of O(n

), where n denotes the total

number of vertices in the bipartite graph. Finding the

feasible labelling for the new row and column takes

linear time, so it has time complexity of O(n). In

order to find an augmenting path, provided we don’t

find one straight away, we have to modify the labels

of the vertices. This adds at least one edge to the

tree, so in the worst case after n iterations we will

find an augmenting path. Each iteration requires

O(n) operations. The computation of

requires

O(n

) complexity, adding edges from S to Y – T

requires O(n

) operations. Thus, the total complexity

of our algorithm is O(n

5.2 Correctness of the Algorithm

When we add a new pair of vertices to the

maximum-weighted-matched bipartite graph,

feasible labelling for the extended bipartite graph

can be determined by using the labelling on the

already determined max-weighted-matched part of

the graph. After adding the new vertices, all the

matched edges will be in the equality subgraph.

If there is no edge between the new pair of

vertices, then they will be the only unmatched

vertices in the graph. Because there is only a single

unmatched vertex pair, it is possible to find only a

single augmenting path in the equality subgraph. So

INCREMENTAL MAINTENANCE OF ONTOLOGIES BASED ON BIPARTITE GRAPH MATCHING

447

when the augmenting path is discovered and the

matching inverted, the size of the matching must

only be increased by one. This in turn would give us

the perfect matching.

If we don’t discover an augmenting path, we

modify the vertex labels to add another edge to the

tree. In the end, an augmenting path starting with the

only unmatched vertex in one partition and ending

with the only unmatched vertex in the other partition

will be discovered. That equality subgraph will

contain the perfect matching or the max-weighted

matching of the bipartite graph.

6 PERFORMANCE ANALYSIS

We implemented our algorithm in Java and tested it

on a Windows operating environment under optimal

conditions.

6.1 Experimental Results

Environment: The code was tested on a Windows

System, running Windows Vista Home Premium,

Intel Core 2 Duo 2.4 GHz with 2037 MB of RAM.

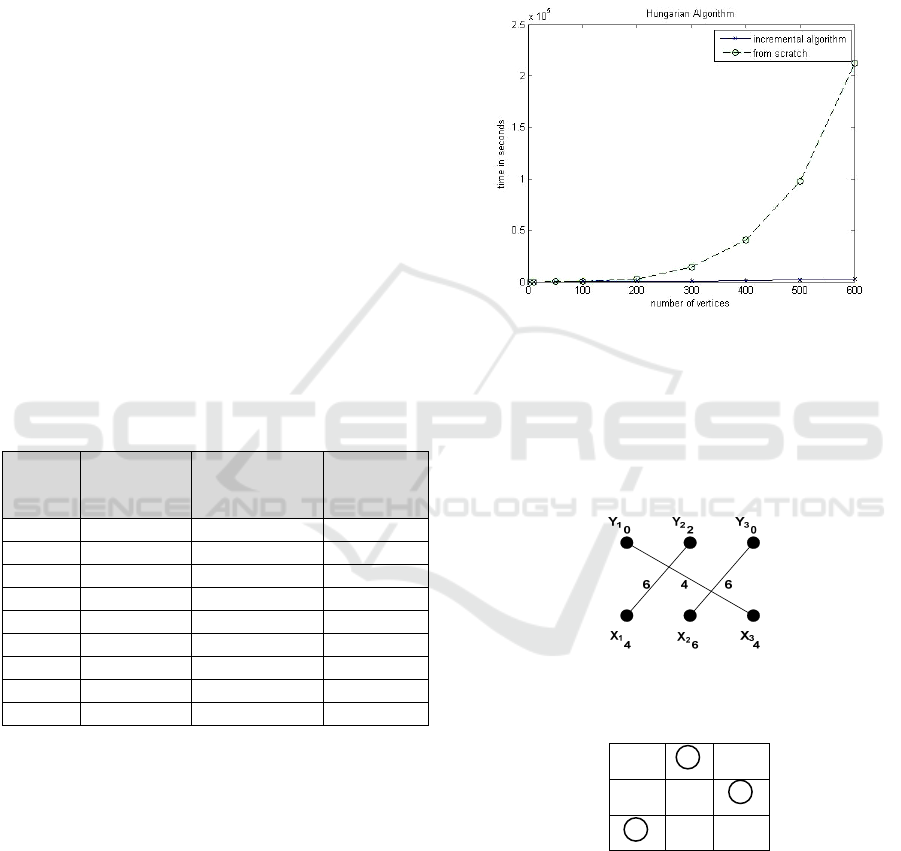
Table 3: Computation Time.

No.

Nodes

Hungarian

Algorithm

(ms)

OntoMaintain

Algorithm

(ms)

From

Scratch

(ms)

3 0 0 0

10 0 0 0

50 16 0 31

100 187 16 202

200 2980 140 2777

300 14118 312 14102

400 39873 1280 40528

500 91369 2168 97407

600 209602 2824 212206

In Table 3: Column 1. Shows number of nodes,

column 2. Shows time taken to run the original

algorithm, column 3. Shows time taken to run the

incremental algorithm and column 4. Shows time

taken to recalculate matching from scratch.

6.2 Performance Graph

The performance results of our algorithm are shown

in Figure 7 below. As is evident from the graph, the

time taken by the Incremental Algorithm to calculate

the new matching is significantly less than the time

taken to run the complete algorithm from scratch.

Until 50 nodes, the Incremental Algorithm takes

about the same time as the Hungarian run from

scratch. However with 100 nodes and onwards, the

Incremental Algorithm takes dramatically less time

to calculate the new perfect matching than the

Hungarian Algorithm run from scratch. As the

number of nodes in the graph increases, a significant

difference in performance time is observed.

Figure 3: Performance Graph.

6.3 An Illustrative Example

The max-weighted matching M*

among the first V

vertices of the partition and the corresponding

weight matrix are displayed in Figure 4a. and Figure

4b.

Figure 4a: Max-weighted matching M*V.

Figure 4b: Weight Matrix.

Now consider the (V + 1) x (V + 1) weight matrix

W’ in Figure 4c. The last row and column

correspond to the newly added vertices. Feasible

labels are assigned to X

and Y

as discussed in

Section 4.1

0 6 0

0 0 6

4 0 0

WEBIST 2009 - 5th International Conference on Web Information Systems and Technologies

448

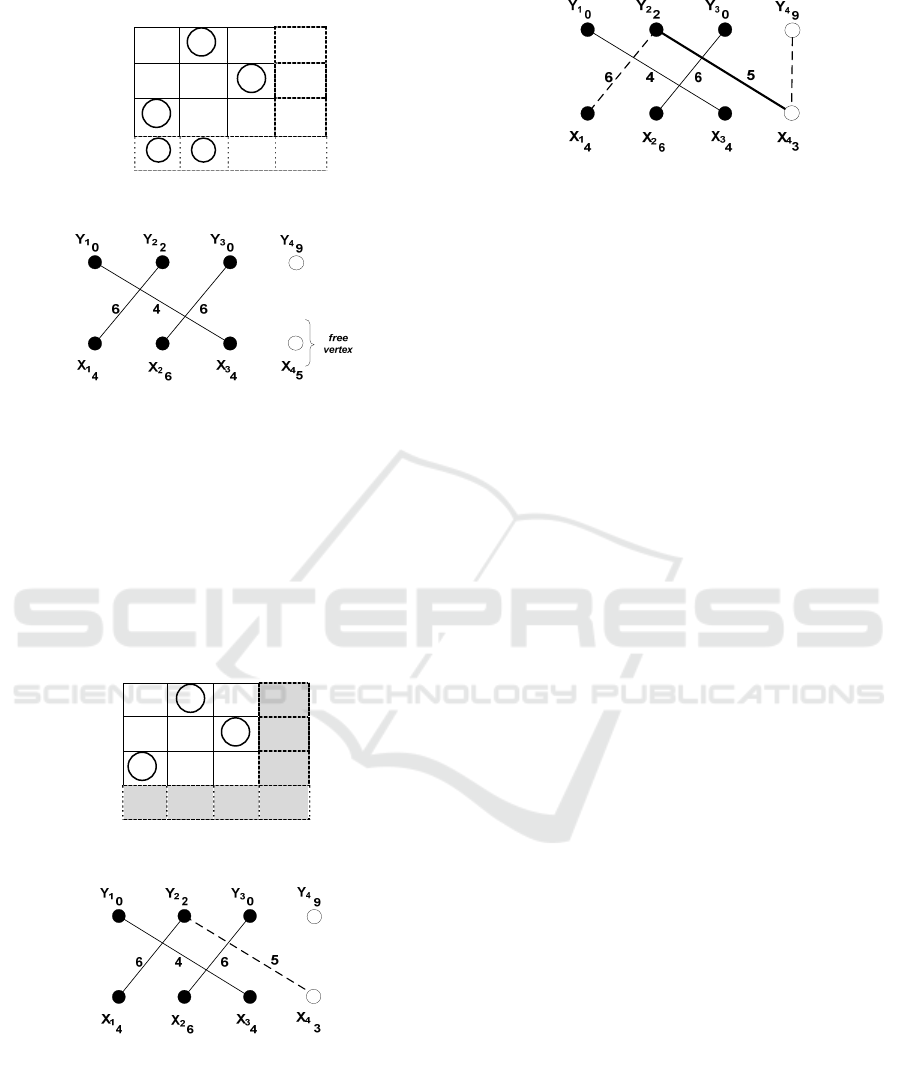
0 Y

2 Y

0 Y

Figure 4c: Extended Weight Matrix W’.

Figure 4d: Unsaturated nodes X

and Y

In Figs. 4c and 4d X

and Y

are the only unsaturated

vertices and there is no augmenting path in the

equality graph, so we revise labels. Figure 5a shows

the new labelling after labels are revised using Step

4 of OntoMaintain. Figure 5b shows the equality

subgraph corresponding to the new labelling; the

augmenting path, in bold, is shown in the Final

Matching in Figure 5c.

0 Y

2 Y

0 Y

Figure 5a: New Labelling.

Figure 5b: Equality Subgraph.

Figure 5c: Final Matching.

REFERENCES

Bellur, U., Kulkarni, R., 2007. Improved Matchmaking

Algorithm for Semantic Web Services Based on

Bipartite Graph Matching In IEEE International

Conference on Web Services (ICWS 2007), July 9-13,

2007, Salt Lake City, Utah, USA, pp. 86-93.

Doan, A., Madhavan, J., Domingos, P., Halevy, A., 2002.

Learning to Map between Ontologies on the Semantic

Web In Proceedings of the Eleventh International

World Wide Web Conference, WWW2002, Honolulu,

Hawaii, USA, 7-11 May 2002. ACM, 2002, pp.662-

673.

Gene Ontology (GO). http://www.geneontology.org/

Gruber, T.R., 1993. A Translation Approach to Portable

Ontology Specification. Knowledge Acquisition, 5(2),

1993, 199-220.

Kuhn, H., 1955. The Hungarian method for the assignment

problem. Naval Research Logistic Quarterly.

Melnik, S., Garcia-Molina, H., Rahm, E., 2002. Similarity

Flooding: A Versatile Graph Matching Algorithm and

its Application to Schema Matching, Proceedings of

the 18th International Conference on Data

Engineering, 26 February-1 March 2002, San Jose,

CA. IEEE Computer Society 2002, 117-128.

Mowbray, T.J., Zahavi, R., 1995. The Essential CORBA:

Sytems Integration Using Distributed Objects. New

York: Wiley.

Paolucci, M., Kawamura, T., Payne, T.R., Sycara, K.,

2002. Semantic Matching of Web Services

Capabilities, ISWC 2002, LNCS 2342, pp. 333–347,

Springer Verlag Berlin Heidelberg.

Pinto, H.S., Martins, J.P., 2000. Reusing Ontologies. In

Proc. of AAAI2000 Spring Symposium Series,

Workshop on Bringing Knowledge to Business

Processes, AAAI Press, pp. 77-84.

Reichhardt, T., 1999. It’s sink or swim as a tidal wave of

data approaches. Nature 399 (6736): 517-20.

Song, G., Qian, Y., Liu, Y., Zhang, K., 2006. OASIS: a

Mapping and Integration Framework for Biomedical

Ontologies, Proceedings of the 19th IEEE Symposium

on Computer-Based Medical Systems (CBMS 2006),

22-23 June 2006, Salt Lake City, Utah, USA, pp. 611-

616.

0 1

0 0

0 0 9

3 5 2 1

0 1

0 0

0 0 9

3 5 2 1

INCREMENTAL MAINTENANCE OF ONTOLOGIES BASED ON BIPARTITE GRAPH MATCHING

449