GROUP UP TO LEARN TOGETHER
A System for Equitable Allocation of Students to Groups
V. Deineko, F. O’Brien and T. Ridd
Warwick Business School, the University of Warwick, Coventry, CV4 7LA, U.K.
Keywords: Working teams, Syndicate groups, Collaborative learning, Equitable allocation, Vector packing.
Abstract: Group-based learning is overwhelmingly accepted as an important feature of current education practices.
The success of using a group-based teaching methodology depends, to a great extent, on the quality of the
allocation of students into working teams. We have modelled this problem as a vector packing problem and
constructed an algorithm that combines the advantage of local search algorithms with the branch and bound
methodology. The algorithm easily finds exact solutions to real life problems with about 130-150 students.
The algorithm is implemented in GroupUp – a decision support tool which has been successfully used in the
University of Warwick for a number of years.
1 INTRODUCTION
Group-based learning is overwhelmingly accepted as
an important feature of education methods
nowadays. Researchers-educationalists claim
(Hassanien, 2006; Houldsworth and Mathews, 2000)
that “collaborative work in groups and group
assessment have become integral components of
many undergraduate and postgraduate programmes
in the UK and all over the world” (see also Thorley
and Gregory, 1994; Gunderson and Moore, 2008, for
the theory behind this phenomenon).
As with many other similar courses, team-work
plays an important role in the University of Warwick
MSc and MBA programmes. For example, the
students in our Management Science and
Operational Research MSc, approximately 50 in
number, are assigned to ‘syndicates’, small groups
of 7 or 8 students that work together throughout their
year at Warwick. The performance of a student’s
group will have a great impact upon their final grade
not merely due to the assessed component of their
team-work but also indirectly as a result of the
morale lost by the students in a ‘bad’ group. This
paper describes the process of modelling this
situation from a case study perspective, the
algorithm that has been created to solve it, and the
decision support tool GroupUp which has the
algorithm embedded within it. Our work
differentiates itself from previous work on a number
of counts. Firstly, to the best of our knowledge, the
algorithm is the first to find exact optimal solutions
to this problem and is capable of finding solutions
quickly for problems much larger than those
described in the existing literature (Bacon, Stewart,
and Anderson, 2001; Baker and Benn, 2001; Baker
and Powell, 2002; Dahl and Flatberg, 2004;
Desrosiers, Mladenovich, and Villeneuve, 2005;
Weitz and Jelassi, 1992). Secondly, the algorithm is
implemented in a decision support system with a
well developed interface simplifying related data
manipulations, again, a feature unlike previous
methods.
Given the nature of Operational Research
courses and the nature of Operational Researchers it
is hardly surprising that a sizeable body of literature
has built up relating to the issues surrounding
student group formation. Broadly speaking
approaches break down into two categories, or
schools. The Diversity School holds that groups
should be formed to enhance the learning experience
and this can be achieved by giving students the
opportunity to work together with others very
different from themselves. By contrast the Equality
approach aims at giving each student an equal
chance of success by making groups as identical as
possible. Baker and Powell (2002) look in depth at
solutions to this problem that use, as we will, binary
data structures to represent the characteristics of
each student. They point out that the heuristic
objective functions used to resolve the problem,
whether they stem from a Diversity or Equality
140
Deineko V., O’Brien F. and Ridd T. (2009).
GROUP UP TO LEARN TOGETHER - A System for Equitable Allocation of Students to Groups.
In Proceedings of the First International Conference on Computer Supported Education, pages 140-145
DOI: 10.5220/0001845401400145
Copyright
c
 SciTePress

rationale, mathematically aim at the same goal.
Insofar as this goes we agree, however we would
argue that the data you feed into your algorithm and
in particular the method used to encode it into a
binary structure will differ based on whether you are
grouping with a Diversity or Equality objective.
Furthermore our research is not heuristic in nature
since we search for exact solutions. Consequently
we will state that at Warwick we approach the
problem from an Equality perspective and rephrase
the problem thus
The Equitable Partitioning Problem
Taking a pool of N items with attributes A
1..N,1..S
(of any data type) partition them into K groups such
that one cannot say that any two groups differ for
any non-trivial reason.
As attributes taking into account while allocating
students to groups, we usually consider gender,
nationality, educational backgrounds (first degree),
age. In fact there is no restrictions on the number
and nature of the attributes that can be taken into
account. One may think of adding learning styles,
based e.g. on the well known Honey and Munford
questionnaire (Honey and Munford, 1986) or
personality types such as the Myers Briggs
Personality Type Indicator (Myers and McCaulley,
1985), etc. It is also possible to solve a problem of
“dispersing” previously formed groups (Dahl and
Flatberg, 2004) by adding as an attribute the “old”
group number.
2 DECISION SUPPORT SYSTEM
FOR ALLOCATING STUDENTS
TO EQUITABLE GROUPS
The application GroupUp is an Excel Add-in for
Microsoft Office with a simple interface in Excel.
The engine (the main algorithm for finding an
optimal allocation) is implemented as a DLL module
written in C.
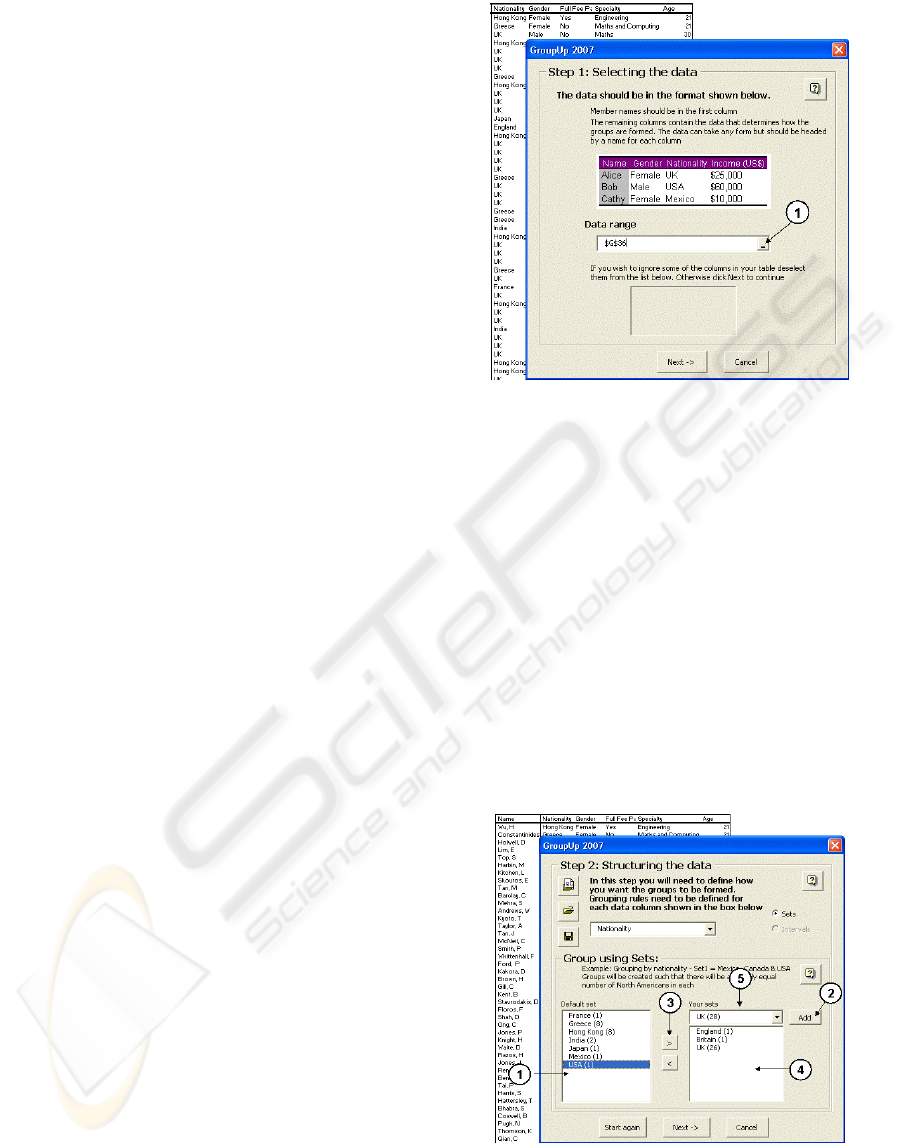
In step one of the allocation process a user is
asked to identify the data set (see Figure 1) and then
to choose the data columns that should be taken into
account.
In the next step of the allocation process the user
is prompted to identify the sets of undistinguishable
items within each attribute. For example, in the
example shown in Figure 2, a set named “UK” is
created to group items with undistinguishable
values. For this step, all attributes with more than
two different values need to be looked through in
order to classify items into undistinguishable sets.
Figure 1: First step in an allocation process: (1) the user is
asked to identify the data set.
For the attributes with numeric values there is an
option of identifying undistinguishable groups
automatically or by defining boundaries for the
intervals (see Figure 3).
In the last step 3 (see Figure 4), the user decides
on the number of groups to be created. With a push
of the button, the job is done!
The results are available in different formats
(tables and charts) and are saved in a new
worksheet.
To simplify the allocation process for subsequent
occasions, an option is provided to save the auxiliary
files enabling the customer decisions at each stage
(undistinguishable attributes, intervals for numeric
data, etc.) to be remembered.
Figure 2: Second step in an allocation process: (1) all
values of an attribute (“nationality” for this picture) are in
the left window; (2) new set – UK – is added; (3) items
with the chosen values of the attribute are moved into the
new set (to be undistinguishable) – (4) and (5).
GROUP UP TO LEARN TOGETHER - A System for Equitable Allocation of Students to Groups
141

Figure 3: For the attributes with numeric values there is an
option of defining intervals (1); based on the total number
of values (2), it is possible to decide on introducing
partitioning points (3) (button (4) to undo the decision) or
use an automatic split (5).
3 INITIAL MODELLING
Our model was created in two stages. The initial
model is very similar to previous approaches to this
problem as tackled by O’Brien and Mingers,
(Mingers and O’Brien, 1995; O’Brien and Mingers,
1997), and Baker and Benn (2001), in that it is a
simple conversion of student attributes to a binary
form.
Figure 4: Decide on the number of groups (1) and push the
button (2). That’s it!
We then constructed the algorithm (and
software) that we shall speak of in Section 5. During
this early developmental stage, a number of
weaknesses were identified in the original model and
the algorithm. By addressing these we eventually
developed a product satisfying us both as researchers
and as customers of a software product.
3.1 The Basic Model
We begin by converting our data into a binary
attribute matrix A where A
ij
= 1 if student i
possesses attribute j. In the case of Gender and other
naturally binary attributes this is a simple case of
Female=1, Male=0. More complicated attributes,
such as Nationality get broken down into multiple
columns i.e. UK=[1,0,0] , Hong Kong=[0,1,0],
Other=[0,0,1]. Our objective is now to get an equal
sum for each binary attribute in each group.
It is reasonable to question whether this
mathematical definition squares with the loose
definition of our objective with respect to numeric
attributes. One of our attributes, Age, takes numeric
values and the natural impulse might be to say that
the most important factor from an equality
perspective is that the mean age should be equal in
each group. Leaving aside the added complexity this
would add to the model we would argue that, though
you can no doubt contrive counter-examples, the
implicit intention of including any attribute, nominal
or numeric, is to create an equal distribution of this
attribute in each group and that a series of binary
categories achieves this in a more satisfactory
manner than means or totals. As example consider
partitioning a set of people with the following ages
[21, 21, 21, 21, 23, 23, 23, 23, 27, 35] in two groups.
Using the mean you would inevitably get
[21,21,21,21,35], [23,23,23,23,27]. Using three
binary columns (Fresh from University, Limited
Experience & Experienced) you would get
[21,21,23,23,27], [21,21,23,23,35]. Though you
may disagree we consider the differences between
the binary groups a lot more trivial than those that
use the mean.
3.2 Objective Function
As Baker and Powell (2002) note there are many
different metrics that can be used as heuristic
objective functions with the aim of equalising
groups however when one is aiming for an exact
solution they all (or rather nearly all, a point which
we will return to in the next section) amount to the
same thing with little to differentiate between them
CSEDU 2009 - International Conference on Computer Supported Education
142

except for speed of calculation. The method we use
is to minimise the integer sum of squared deviations
across groups and attributes. To speed this we
employ the concept of the perfect group with
summed binary attributes t
1..J
. For K groups and N
items the sum of values of attribute j can be
represented as
1
()
N
ij j j j
i
A
Krt r
=
=− +
∑
(r
j
<K)
Put another way if we are going to split 25 men
into 7 groups we will ideally have 3 groups (K-r
j
)
with 3 men (t
j
) in and 4 groups (r
j
) with 4 men (t
j
+1)
in. For convenience sake we take the lower bound,
3, as the ideal number of men in a group. Now for x
ik
= 1 if item i is in group k, the objective function is
2
11 1
JK N
ik ij j
jk i
Z
xA t
== =
⎛⎞
⎛⎞
=−
⎜⎟
⎜⎟
⎝⎠
⎝⎠
∑∑ ∑
Conspicuous by its absence is any scheme for
weighting the columns such that, for example, it
could be made equally important to split up the
single Gender column and the 3 combined columns
of Nationality. We come to this in the next section.
3.3 A Perfect World
A natural extension of the concept of the perfect
group is the concept of a perfect grouping where
each group has either t
j
or t
j
+1 members for each
binary attribute. It may be the case that such a
solution is mathematically impossible for a given
problem and this is the reason we talk of ‘perfect’
solutions rather than ‘optimal’ ones. That said the
‘perfect’ grouping provides us with a convenient
value for the lower bound of our solution
22
min
11
((( 1) ) ( )( )
J
jj j jj j j
jj
J
Z
rt t Krt t r
==
=+−+−−=
∑∑
One of the more astonishing discoveries of this
research is that practical instances of this problem
are, universally in our experience, capable of perfect
solution. It is possible to contrive data sets that are
‘imperfect’ i.e. mathematically incapable of perfect
solution. In fact for any number of students and
groups as few as three binary columns of data are all
that is required. Nevertheless we have found it is
safe to assume that a perfect solution will arise for
all practical data sets. This insight opens up new
possibilities for two reasons. Firstly weighting the
columns becomes completely unnecessary since you
will get a perfect solution for all columns no matter
what the weights are. Secondly, as long as one
doesn’t go wild, it is possible to add new binary
columns without compromising the integrity of an
initial solution. Whilst you may do this by including
more attributes for each student we use this ability to
address the deficiencies in and enhance our basic
model.
4 FURTHER MODELLING
4.1 Natural Binary Attributes
During experimentation a set of results were
produced for a group of 13 students, 6 of whom
were male and 7 female; the students needed to be
divided into three ‘equal’ groups. The Gender
column for this allocation is shown in Figure 5. The
computer claimed that the solution was perfect and
yet Male clearly takes three different values,
something that should not occur in a perfect result.
After searching our code for errors it was discovered
that the solution actually is perfect. Female was
given the binary value 1 and is consequently
distributed evenly with either 2 or 3 women in each
group but because total group size can be either 4 or
5 this meant that the total number of men in each
group could take any of three values. Such a
problem can be resolved by converting Gender into
two binary columns, just as one would with a
multiple value attribute, thus men will be
standardised as well as women. Complicating the
model like this is not always necessary. If each
group was going to be exactly the same size or the
number of women in each group was going to be the
same, the problems of integer division would not
arise. In this instance by making Male = 1 Gender
would require only one binary column as men split
evenly amongst the groups.
Figure 5: The natural binary problem.
GROUP UP TO LEARN TOGETHER - A System for Equitable Allocation of Students to Groups
143

4.2 Group Splitting
A similar problem to that on the MSOR programme
exists on the Warwick MBA. In addition to the basic
equitable partitioning requirement the MBA requires
three iterations of the allocation process to be
conducted, one for each term of study. This requires
that groupings be constructed with the condition that
no students should be in the same group twice.
Initially we attempted to build this into our
algorithm using a technique based on Latin squares
but found that, while the updated algorithm could
handle creating one additional grouping, any further
brought it grinding to a halt. Consequently we
returned to an earlier idea, creating the groupings
one by one and splitting the groups by including
previous group numbers as attributes. “Was in
Group 1” becomes a binary attribute and with luck
people who were previously in Group 1 will all be
separated. We had initially shied away from this idea
on the basis that, since the MBA requires 14 groups
an additional 28 attribute columns (when two
previous groupings are taken into account) would
mean we would end up with a non-optimal answer.
The MBA group-splitting requirement is hard so this
would not be acceptable. We now use a hybrid of the
two methods with one previous grouping split up
algorithmically and all subsequent ones split up
using attributes.
4.3 Sparsity
Another aspect of the MBA problem caused us to
add bonus columns to our data structure. The fact
that it is a much larger problem, coupled with a
requirement for a much finer partitioning of
attributes leads to a situation where the basic model
detailed above can result in groups with significant
non-trivial differences. Mingers and O’Brien (1995)
worked on the same MBA problem and took the
view that, when it comes to attributes such as
Nationality it is more important to have an equal
number of nationalities represented in each group
than equal numbers of students of each nationality.
In figure 6 you can see two extreme examples which
illustrate the fallacies of both our methods. Mingers
and O’Brien’s (1995) model could, in theory, lead to
an optimal grouping with six UK students in one
group and only one in another whilst our basic
model, on the other hand, could lead to seven
nationalities being represented in one group and only
three in another.
The problem for our model arises due to integer
division and what we term ‘sparse’ attributes,
minorities such as Spain above where there are not
enough people to have one in each group. To see
how the problem arises take 3 UK students and one
Canadian and put them into two groups. You will
naturally get 2 UK in one group, one UK and the
sparse Canadian in another. Add in three Chinese
students and a sparse Spaniard and you could get
one group with 2 UK students and 2 Chinese with
the other group being composed of 4 different
nationalities.
Figure 6: The problem of sparsity.
Of course the position might be reversed so that
the new groups have three nationalities each but
since there is no control mechanism in the basic
model to ensure this, sparse columns do present a
problem.
We have resolved the sparse problem by taking
into account that in a perfect grouping the number of
nationalities represented in a group is equal to the
number of standard categories, for there must be at
least person from each of these categories in each
group, plus the number of people from sparse
categories in that group, each of which must come
from a different nationality. Where appropriate a
new binary attribute is added to our model for each
column with more than one sparse category. The
new attribute, IsSparse, takes the value 1 for all
items that are in a sparse category. In a new perfect
grouping the number of people from sparse groups
will be evenly distributed, as far as integer division
will permit, and hence the problem is resolved. It is
true that this method does not by necessity provide
an optimal solution in terms of Mingers and
O’Brien’s (1995, 1997) model however the
difference is negligible and in terms of achieving our
overall goal, namely groups with no significant
differences, it is difficult to see how this composite
model could be improved upon.
CSEDU 2009 - International Conference on Computer Supported Education
144

5 CONCLUSIONS
The problem of allocating students to equitable
working teams is a well known practical problem –
many Higher Education institutions throughout the
world face this problem when trying to improve the
learning process for their students. GroupUp is a
simple tool to resolve this problem in practice (a trial
version of the software is available on request from
[e-mail]). We are now planning to
undertake some extensive collaborative research
with both practitioners and researchers in the field of
education. This collaboration will explore how
different rules for constructing the groups influence
both the group dynamics and the efficiency and
effectiveness of group performance.
REFERENCES
Bacon, D. R., Stewart K. A., Anderson, E. S., 2001.
Methods of assigning players to teams: A review and
novel approach. Simulation & Gaming, 32(2), pp 6-17.
Baker, B. M., Benn, C., 2001. Assigning pupils to tutor
groups in a comprehensive school. Journal of the
Operational Research Society, 52(4), pp 623-629.
Baker, K. R., Powell S. G., 2002. Methods for assigning
students to groups: a study of alternative objective
functions. Journal of the Operational Research
Society, 53(4), pp 397-404.
Caprara, A., Toth, P. 2001. Lower bounds and algorithms
for the 2-dimensional vectorpacking problem, Discrete
Applied Mathematics, 111, pp 231-262.
Checuri, C., Khanna, S., 1999. On multi-dimensional
packing problems. In: Procedings of the tenth annual
ACM-SIAM Symposium on Discrete algorithms.
(SODA’99), ACM Press, New York, pp 185-194.
Garey, M. R., Graham, R. L., Johnson, D. S., and Yao, A.
C., 1976. Resource constrained scheduling as
generalized bin-packing, Journal of Combinatorial
Theory (A), 21, pp 257-298.
Dahl, G., Flatberg, T., 2004. Some constrained
partitioning problems and majorization, European
Journal of operational Research, 158, pp 434-443.
Desrosiers, J., Mladenovic, N., and Villeneuve, D., 2005.
Design of balanced MBA student teams, Journal of
the Operational Research Society, 56(1), pp 60-66.
Gunderson, D. E., Moore, J. D., 2008. Group learning
pedagogy and group selection, International Journal of
Construction Education and Research, 4(1), pp 34-45.
Han, B. T., Diehr, G., and Cook, J. S., 1994. Multiple-
type, two dimensional bin packing problems:
applications and algorithms, ANN Operations
Research Society, 50, pp 239-361.
Hassanien, A., 2006. Student experience of group work
and group assessment in higher education, Journal of
teaching in travel & tourism, 6(1), pp 17-39.
Holyer, I., 1981. The NP-completeness of edge-colouring.
SIAM J Comput 10(4), pp 718-720.
Honey, P., Mumford, A., 1986. The manual of Learning
Styles, Revised edn, Mumford, P., Maidenhead.
Houldsworth, C., Mathews, B.,2000. Group composition,
performance and educational attainment, Education
and Training, 42 (1), pp 40-53.
Huxham, M., Land, R., 2000. Assigning students in group
projects. Can we do better than random? Innovation in
Education & Training International, 37(1), pp 17-22.
Mingers, J., O’Brien, F. A., 1995. Creating student groups
with similar characteristics: a heuristic approach,
Omega, Internationsl Journal of Management Science,
23 (3), pp 313-321.
Myers Briggs, I and McCaulley, M, 1985. A guide to the
development and use of the Myers- Briggs Type
Indicator. Consulting Psychologists Press: Palo Alto:
California.
O’Brien, F. A., Mingers, J., 1997. A heuristic algorithm
for the equitable partitioning problem, Omega,
Internationsl Journal of Management Science, 25 (2),
pp 215-223.
Spieksma, F. C. R., 1994. A branch-and-bound algorithm
for the two-dimentional vector packing problem,
Computers & Operations Research, 21, pp 19-25.
Thorley, L., Gregory, R., (eds), 1994. Using Group-based
Leraning in Higher Education, Kogan Page, London.
Weitz, R. R., Jelassi, M. T., 1992. Assigning students to
groups: a multi-criteria decision support system
approach, Decision Sciences, 23 (3), pp 746-757.
GROUP UP TO LEARN TOGETHER - A System for Equitable Allocation of Students to Groups
145