FREQUENCY ASSIGNMENT OPTIMIZATION USING THE

SWARM INTELLIGENCE MULTI-AGENT BASED ALGORITHM

(SIMBA)

Grant Blaise O’Reilly

Academy for Information Technology, University of Johannnesburg, Auckland Park, Johannesburg, South Africa

Keywords: Swarm intelligence, Stigmergy, Multi-agent system, Frequency assignment problem.

Abstract: The swarm intelligence multi-agent based algorithm (SIMBA) is presented in this paper. The SIMBA

utilizes swarm intelligence and a multi-agent system (MAS) to optimize the frequency assignment problem

(FAP). The SIMBA optimises by considering both local and global i.e. collective solutions in the

optimization process. Stigmergy single cell optimization (SSCO) is also used by the individual agents in

SIMBA. SSCO enables the agents to recognize interference patterns in the frequency assignment structure

that is being optimized and to augment it with frequency selections that minimized the interference. The

changing configurations of the frequency assignment structure acts as a source of information that aids the

agents when making further decisions. Due to the increasing demand of cellular communication services

and the available frequency spectrum optimal frequency assignment is necessary. The SIMBA was used to

optimize the fixed-spectrum frequency assignment problem (FS-FAP) in cellular radio networks. The results

produced by the SIMBA were benchmarked against the COST 259 Siemens scenarios. The frequency

assignment solutions produced by the SIMBA were also implemented in a commercial cellular radio

network and the results are presented.

1 INTRODUCTION

The demand for cellular communication services is

constantly growing. However, due to the limited

frequency spectrum available to cellular network

operators the efficiency in which the frequency

spectrum is utilized is a very important issue. This is

the reason why the frequency assignment problem

has attracted a large amount of interest. The efficient

use of radio spectrum and the minimization of

interference is the main goal of any frequency

assignment algorithm.

The frequency assignment problem (FAP) in its

simplest form is equivalent to the generalized graph-

colouring problem (Hale, 1980). Thus it is also an

N-P complete problem (Hale, 1980). Searching for a

solution to the frequency assignment problem

increases exponentially with the number of cells in

the radio network. In this paper the swarm

intelligence multi-agent based algorithm (SIMBA)

will be presented and discussed. SIMBA is an

algorithm inspired by swarm intelligence. The

SIMBA was implemented using a multi-agent

system (MAS). Agents in the multi-agent system of

SIMBA consider both local and global solutions

when optimizing the fixed spectrum frequency

assignment problem (FS-FAP). The local solution is

the frequency assignment solution produced by the

individual agent. The global solution is the best

frequency assignment solution (solution with the

least interference) produced by the collective. The

design of the SIMBA as well as the MAS supporting

the SIMBA will be described in depth. The results

produced by the SIMBA will be compared to the

COST 259 Siemens bench marks (Eisenblätter and

Koster, 2008). The frequency assignment solutions

produced by SIMBA were implemented in a

commercial, operational cellular radio network and

the results are presented in this paper.

Stigmergy single cell optimization (SSCO) was

utilised by the individual agents in the SIMBA in

order to make intelligent decisions on the next

frequency that needed to be selected. SSCO is based

on stigmergy. The actual structure that the agents are

working on actually guides the agents on their future

decisions. SSCO enables the agents to recognize

interference patterns in the frequency assignment

structure that is being optimized. These interference

Blaise O’Reilly G. (2009).

FREQUENCY ASSIGNMENT OPTIMIZATION USING THE SWARM INTELLIGENCE MULTI-AGENT BASED ALGORITHM (SIMBA).

In Proceedings of the 11th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

25-32

DOI: 10.5220/0001857600250032

 SciTePress

patterns then stimulate the agent to select a

frequency that minimises this interference pattern.

The SIMBA has shown promising improvements

both in the efficiency of the resultant solution and

the time it took to find an acceptable solution. The

efficiency of the resultant solutions has been tested

against a number of cellular radio network

measurement parameters. These parameters

indicated the quality in a cellular radio network after

a frequency assignment solution is implemented.

These parameters will also be discussed briefly.

2 THE FIXED-SPECTRUM

FREQUENCY ASSIGNMENT

PROBLEM

The FS-FAP can be represented by a weighted,

undirected graph G with a set of vertices V and a set

of edges E (Montemanni et al., 2003). Formally, it is

a quadtuple FS-FAP = {V, E, D, P} with

• Every transceiver in the frequency

assignment problem is represented by a

vertex v where v Є V. Every vertex

represents a transmitter of the original

frequency assignment problem

(Montemanni et al., 2003).

• Interference between two transceivers is

represented by an edge. Edges will be

written as {v, u} (Montemanni et al., 2003).

• A label on the edges will be described by D

such that the edge {v, u} is mapped to d

N where N={x|x is a positive integer or

zero}. d

will be defined as the highest

separation that may cause unacceptable

interference between frequencies assigned

to transceivers u and v. The frequency

assigned to transceiver v is denoted by f(v)

and similarly the frequency assigned to

transceiver u is denoted by f(u). If |f(v) –

f(u)|> d

, then the interference between the

frequencies on transceiver v and u is

acceptable (Montemanni et al., 2003).

• A label on the edges will be described by P

such that the edge {v, u} is mapped to p

N where N={x|x is a positive integer or

zero}. p

is defined as the cost to be paid if

the separation between the frequencies

assigned to transmitters v and u is less than

or equal to d

(Montemanni et al., 2003).

The cost of the total interference in the

frequency assignment problem is given by

the following cost function:

∑

≤−

∈

ufvf

Euv

SCos

|)()(|

;},{

)(

(1)

where the solution representation of a

frequency assignment S will be represented

by using a list

(0), f

(1), f

(2),…, f

(v),…, f

(|V|-1)>

where the v

element contains the frequency

assigned to transceiver v.

The objective of the FS-FAP is to find an

assignment that minimizes the sum of p

over all

pairs for which |f(v) – f(u)|≥ d

(Montemanni et al.,

2003).

3 STIGMERGY SINGLE CELL

OPTIMIZATION

In a cellular network each cell is served by a small

number of transmitters (usually 1-9). With exception

of the broadcast control channel (BCCH) the

constraints applied to the frequency assignment of

each transceiver (TRX) in the cell may be identical.

Due to the BCCH being a critical channel the

constraints (frequency separation or penalties)

associated with this channel are usually very high.

Thus, stigmergy single cell optimization (SSCO) is

an appropriate technique that can be used only in

cellular telecommunication networks.

Stigmergy single cell optimization (SSCO)

allows one to fix all the frequencies assigned to a

single cell’s interferers. The frequencies of this

single cell’s transceivers can then be optimized

according to the interference patterns that emerge

when certain frequencies are selected. If large

interference patterns emerge when a frequency is

selected then the frequency is discarded. If no

interference or minimal interference patterns are

experienced by the selection of a frequency then the

frequency is accepted. The actual structure of the

frequency assignments and the interference patterns

created by the frequency selections is constantly

influencing the decision of the agent. It is proposed

that an agent will change the frequencies on the

transceivers according to the structure of the current

interference pattern in the frequency assignment

structure. The frequency assignment working

solution will represent the structure the agent is

building. The agent will approach each transceiver

and change its frequency to the current best

frequency. The current best frequency has the least

amount of interference. Once the new frequency has

been assigned to the transceiver the cost of the

frequency assignment solution is calculated using

ICEIS 2009 - International Conference on Enterprise Information Systems

equation 1. The agent will be stimulated to accept a

configuration change where the interference pattern

(i.e. cost) was decreased and repel a change that

increased the interference.

The analogy to stigmergy comes from the fact

that stigmergy is the coordination of tasks and

regulation of constructions (e.g. a termite mound in

a termite colony) in an environment that depends not

on the entities, but on the constructions themselves

(Kristensen, 2000 and Valckenaers et al., 2001). The

entities do not direct the work but are guided by it.

Structure construction e.g. nest building in social

wasps is an example of this form of communication.

Agents recognize patterns in a structure that is being

built and are able to augment it with new

components. The changing configurations of the

structure act as a source of information that aids the

agents when making further decisions. The agents

are stimulated by the change in the configuration of

the structure and respond accordingly (Bonabeau et

al., 1999). Social wasps have the ability to build

highly organized construction i.e. nests. These

structures can range from a few cells to millions of

cells packed in stacked combs. Studies have shown

that these building characteristics consist of a series

of if-then decision loops (Bonabeau et al., 1999).

Each stage of the nest stimulates the wasps to

respond in a certain manner.

3.1 Implementing the Stigmergy Single

Cell Optimization

The list of fixed frequencies in the network’s

allocated spectrum will be represented by L. Each

frequency is tested using the SSCO. A priority queue

will be created with the priority ranked according to

the frequency causing the least amount of

interference. When a frequency is requested from

the priority queue the frequency with the least

amount of interference is returned. This is the best

current frequency that can be used.

The priority queue calculates the priority of the

frequencies with minimum interference by taking as

input the transceiver T. Through an iterative process

the transceiver T will be set to each frequency in the

fixed frequency list L, respectively. For each

frequency in the list L that is set to the transceiver T

the cost of the total interference is calculated i.e. an

interference pattern is determined. Thus each

frequency in L will have an associated interference

cost. The list L is then sorted in a descending order

with the frequency with the lowest interference cost

at the top of list L. When requested the priority

queue will return the top element or highest priority

element from the list L i.e. the frequency with the

lowest interference cost.

When the agent is executing the algorithm it will

iterate through every transceiver in the FAP. When a

certain transceiver v is selected by the agent it will

select the best current frequency. The agent does this

by requesting the frequency from the priority queue.

The frequency is then removed from the priority

queue. This process is repeated until a frequency is

found that does not cause any violations (i.e.

minimizes the interference pattern) and is not in the

pheromone list (see section 3.2). Once a frequency is

found it is assigned to the transceiver v. The cost is

then calculated for the new solution S i.e. Cost(S). If

the Cost(S) is less than the previous cost i.e.

Cost(S

) plus a threshold value i.e. Cost(S) –

Cost(S

) ≤ threshold then the frequency assigned

to v is accepted. However, if Cost(S) – Cost(S

) >

threshold then the frequency assigned to v is rejected

and the transceiver v reverts back to its previous

frequency.

3.2 The Analogy to Stigmergy

The structure of the frequency assignment solution

influences how the agent assigns frequencies to the

different transceivers. The structure seems to

provide enough constraints to direct the selection of

frequencies. Frequencies are not just added or

changed randomly. The agent is influenced by

previous frequency assignments. Assignment

decisions seem to be made locally on perceived

configurations in a way that possibly constrains the

assignment dynamics.

The second type of stigmergy built into the

algorithm is short term memory via pheromones.

This is very similar to a dynamic tabu list which has

been used successfully in a number of optimization

algorithms (Montemanni et al., 2003, Hao et al.,

1998). Each time a frequency is assigned to a

transceiver a pheromone is created and added to the

pheromone list. A pheromone is a structure

containing the transceiver identity, the frequency

and a duration variable. The pheromone list is a

first-in-first-out queue of pheromones. The time the

pheromone resides in the pheromone list is

equivalent to the time it would take for the

pheromone to dissolve. The pheromone is constantly

dissolving in nature. To model this behavior the

duration variable in the pheromone is incremented

every time a frequency is assigned to a transceiver.

The pheromone list is a fixed size M. If the duration

variable is greater than M then the pheromone is

removed from the pheromone list i.e. it has

dissolved.

FREQUENCY ASSIGNMENT OPTIMIZATION USING THE SWARM INTELLIGENCE MULTI-AGENT BASED

ALGORITHM (SIMBA)

When the current best frequency is selected it is

also checked against the pheromone list. If the

current best frequency and transceiver that is busy

being changed are matched against an existing

pheromone in the pheromone list then that current

best frequency is ignored and the next best

frequency is selected from the priority queue. This

technique allows the search to explore new areas in

the search space and to escape local minima

(Michalewicz et al., 2007). The general idea behind

pheromones in the algorithm is to ensure that certain

changes made in the assignment solution are

undisturbed for a certain amount of time or future

iterations. This forces the algorithm to explore other

parts of the search space and after a certain amount

of time or after a number of iterations have elapsed

these frequencies would become available again

(Michalewicz et al., 2007). A β variable was also

introduced into the algorithm to reduce the size of

the pheromone list M. The pheromone list will

reduce over time by setting the size of the

pheromone list T

= β* T

. The longer the

algorithm executes the shorter the dissolve period

for a pheromone. The reason for the reduction of the

pheromone dissolve period is that the closer the

algorithm moves to an optimized solution the more

focused the search should be.

4 SWARM INTELLIGENCE

MULTI-AGENT BASED

ALGORITHM (SIMBA)

The pseudo code below describes the spectrum

priority queue used in the algorithm. The purpose of

the spectrum priority queue was to produce a

priority queue with the best current frequencies to

use. The pseudo code utilizing the spectrum priority

queue would remove the first element in the priority

queue to find the current best frequency to use.

PriorityQueue

spectrumPriorityQ(transceiver v)

begin

Instantiate PriorityQueue PQ

foreach frequency f do

begin

oldFreq = v.getFrequency

v.setFrequency(f)

cost = Cost(S)

PQ.add(KeyValuePair<f,cost>)

end

v.setFrequency(oldFreq)

return PQ.sorted

end.

The allow assignment pseudo code described

below determines whether the current best frequency

selected from the priority queue will be used or not.

If the frequency is in the pheromone list then it is not

allowed to be used. Similarly, if the frequency

causes violating transceivers i.e. the transceivers

does not obey co-site and co-cell separation

constraints it is not allowed to be used. Violating

transceivers cause an increase in the interference

pattern. Co-site is defined as transceivers sharing the

same site and co-cell is defined as transceivers

sharing the same cell. The allow assignment method

returns the frequency that does not cause any

violating transmitters or that does not reside in the

pheromone list otherwise it returns -1.

int AllowAssignment(transceiver v,

PriorityQueue PQ)

begin

while (not PQ.isEmpty)

begin

KeyValuePair<frequency,cost>KVP =

PQ.getFirst()

PQ.removeFirst()

if(not inPheromoneList

(v,KVP.frequency))

AND

(not violatingTransmitter

(v,KVP.frequency))

return KVP.frequency

end

return -1

end.

The multi-agent framework for the SIMBA is

comprised of the agents executing the SIMBA and a

repository for the global best solution found (see

figure 1). Each agent contains a working solution S

for the frequency assignment problem as well as a

local best solution. The local best solution is the best

solution found by the individual agent. The working

solution S is the solution that is constantly changing

as the search is taking place. Each agent is able to

access the repository for the best global solution. If

at any time during the execution of the algorithm an

agent’s local best solution is better than the global

best solution i.e. the total interference in the local

best solution is less than the total interference in the

global best solution then the global best solution is

replaced with the agent’s local best solution. At this

point in time the remainder of the agents in the

system excluding the agent that found the new

global best solution will perform a transformation on

their working solutions (see figure 1). The

transformation process performed by the agent

merges its current locally best solution with the new

global best solution. The merge is dependent on two

variables Φ

and Φ

. Φ

is the percentage of the local

ICEIS 2009 - International Conference on Enterprise Information Systems

solution that will be merged into the new working

solution and similarly Φ

is the percentage of the

global solution that will be merged into the agent’s

new working solution. Selecting Φ

> Φ

allows the

merge to put more trust in the global solution i.e. it

places more trust in the swarm solution than its own

local solution. In this case more of the merged

solution will be made up of the global solution than

the previous local solution.

Figure 1: Multi-agent system supporting SIMBA.

The merge method in the swarm interaction takes

as input parameters the local and global frequency

assignment solutions as well as the two variables Φ

and Φ

. N

local

= Φ

*(total number of TRXs) and

global

= Φ

*(total number of TRXs). N

local

will be

the number of transceivers (including the set

frequency) selected from the local solution.

Similarly, N

global

will be the number of transceivers

(including the set frequency) selected from the

global solution. A transceiver selected into N

local

cannot be selected into N

global

and similarly a

transceiver selected into N

global

cannot be selected

into N

local

. The new merged solution is N

global

local

The Swarm Intelligence Multi-agent Based

Algorithm (SIMBA) is described below.

SIMBA

begin

= 0; T

= 500; I

reduce

= 5*10

;

= 30 → 40; Φ

= 60 → 70;

Threshold = 1 → 10; alpha = 0.99;

beta =0.999;

S = randomly generate solution for

FAP

foreach transceiver v do

begin

newFreq = AllowAssignment

(v,spectrumPriorityQ(v))

if (newFreq not equal to -1) then

begin

oldFreq = v.getFrequency()

prevCost = Cost(S)

v.setFrequency(newFreq)

UpdatePheromoneList

(new Pheromone(newFreq,v,0))

if ((Cost(S) – prevCost)

> Threshold) then

v.setFrequency(oldFreq)

else

begin

if(Cost(S) < Cost(localBest))

localBest = S

SwarmInteraction(this,Φ

,Φ

)

end

++;

If (I

reduce

equals N

) then

begin

= 0;

= T

*beta;

Threshold = Threshold*alpha

end

end.

The multi-agent system is based on a social

model that is based on swarm intelligence. Each

agent is making use of its own local search

knowledge as well as knowledge from the swarm as

a whole to find an optimized solution.

void SwarmInteraction

(SIMBAAgent agent, Φ

, Φ

)

begin

if (Cost(agent.localBest) <

Cost(globalBest)) then

begin

globalBest = agent.localBest

GlobalBest.setFound(TRUE);

end

if (GlobalBest.getFound())

begin

agent.S = Merge(agent.localBest,

globalBest,Φ

,Φ

)

end

end.

5 COST 259 BENCHMARKS

AUTHOR(S)

The effectiveness of the SIMBA is demonstrated by

applying the SIMBA to the COST 259 benchmarks

FREQUENCY ASSIGNMENT OPTIMIZATION USING THE SWARM INTELLIGENCE MULTI-AGENT BASED

ALGORITHM (SIMBA)

(Eisenblätter and Koster, 2008). These instances are

widely used in the mobile telephone industry. The

largest problem considered (Siemens 4) had 2780

transceivers. The best cost values found by the

SIMBA for the Siemens instances were compared to

the following:

• DTS (Glamorgan) a dynamic tabu search method

(Eisenblätter and Koster, 2008).

• K-THIN(UR1) a simulated annealing combined with

dynamic programming to compute local optima

method (Mannino et al., 2000).

• SA(TUHH) a simulated annealing (Beckmann and

Killat, 1999).

• TA(RWTH) a threshold accepting method

(Hellebrandt and Heller, 2000).

• TA(Siemens) a threshold accepting method

(Hellebrandt and Heller, 2000).

• U(Siemens) an unknown method (Eisenblätter and

Koster, 2008).

• SEMA, the Swarm Effect minimization algorithm

(O’Reilly and Ehlers, 2008)

Table 1: Siemens 1, GSM 900 network with 179 active

sites, 506 cells, and an average of 1.84 TRXs per cell. The

available spectrum consists of two blocks containing 20

and 23 frequencies, respectively.

App Cost Co Adj TRX

TRX pairs exceeding

.01 .02 .03 .04

K-THIN 2.20 0.03 0.03 0.05 33 4 1 0

TUHH 2.78 0.04 0.04 0.08 60 14 6 0

RWTH 2.53 0.03 0.03 0.06 48 11 3 0

TA 2.30 0.03 0.03 0.05 43 7 2 0

U 3.36 0.05 0.04 0.12 78 25 10 3

SEMA 2.35 0.03 0.03 0.06 44 9 2 0

SIMBA 2.26 0.03 0.03 0.05 39 7 1 0

Table 2: Siemens 2, GSM 900 network with 86 active

sites, 254 cells, and an average of 3.85 TRXs per cell. The

available spectrum consists of two blocks containing 4 and

72 frequencies, respectively.

App Cost Co Adj TRX

TRX pairs exceeding

.01 .02 .03 .04

DTS 14.28 0.11 0.02 0.20 343 89 24 18

K-THIN 14.27 0.07 0.02 0.16 359 71 27 17

TUHH 15.46 0.07 0.02 0.18 404 109 42 20

RWTH 14.75 0.06 0.02 0.17 268 91 34 13

TA 15.05 0.11 0.02 0.20 381 92 37 15

U 17.33 0.08 0.02 0.20 462 148 47 18

SEMA 14.86 0.08 0.02 0.17 364 87 41 14

SIMBA 14.34 0.08 0.02 0.20 360 77 33 13

The results from these methods were obtained

from the FAP website (Eisenblätter and Koster,

2008) and are presented in tables 1 to 4. The

comparison of these results and the results obtained

with the SIMBA are also presented in tables 1 to 4.

The columns described in tables 1 to 4 are the total

cost, the maximum co-channel, adjacent channel and

TRX values as well as the total number TRX pairs

exceeding an interference of x where xЄ(0.01, 0.02,

0.03, 0.04). The emphasis was on the ultimate

quality of the solution that SIMBA produced within

limited time constraints. The time constraints set for

SIMBA were 24 hours where many of the other

algorithms ran for several days.

Table 3: Siemens 3, GSM 900 network with 366 active

sites, 894 cells, and an average of 1.82 TRXs per cell. The

available spectrum comprises 55 contiguous frequencies.

App Cost Co Adj TRX

TRX pairs exceeding

.01 .02 .03 .04

DTS 5.19 0.04 0.03 0.07 88 14 3 0

K-THIN 4.73 0.03 0.02 0.08 80 6 0 0

TUHH 6.75 0.05 0.03 0.11 137 31 9 2

RWTH 5.63 0.03 0.03 0.07 103 15 3 0

TA 5.26 0.04 0.03 0.07 87 10 3 0

U 8.42 0.05 0.04 0.12 188 47 18 6

SEMA 5.76 0.03 0.03 0.08 101 28 3 0

SIMBA 5.24 0.03 0.03 0.08 83 11 3 0

Table 4: Siemens 4, GSM 900 network with 276 active

sites, 760 cells, and an average of 3.66 TRXs per cell. The

available spectrum comprises 39 contiguous frequencies.

App Cost Co Adj

TRX pairs exceeding

.01 .02 .03 .04

DTS 81.88 0.20 0.05 0.43 2161 971 547 344

K-THIN 77.25 0.19 0.05 0.36 2053 871 445 282

TUHH 89.15 0.24 0.03 0.53 2350 1056 591 368

RWTH 83.57 0.18 0.04 0.35 2251 1006 540 343

TA 80.97 0.17 0.03 0.36 2143 933 502 328

U 105.8 0.27 0.04 0.53 2644 1286 798 562

SEMA 81.96 0.21 0.05 0.48 2181 991 549 353

SIMBA 81.91 0.21 0.05 0.48 2178 990 549 353

6 CELLULAR RADIO NETWORK

PARAMETER DESCRIPTION

The SIMBA was tested on a commercial mobile

telecommunications network in South Africa. The

frequency assignment solution produced by SIMBA

was applied to an operational base station controller

(BSC). There were 349 cells with an average of 3

transmitters per cell on the BSC. The available

spectrum consisted of two blocks containing 24 and

31 frequencies, respectively. In order to appreciate

the results produced in this paper a brief explanation

needs to be given of the mobile telecommunications

parameters utilized.

ICEIS 2009 - International Conference on Enterprise Information Systems

The %DROP (percent drop) parameter

represents the percentage of abnormal

disconnections (drop calls) on the BSC in a mobile

cellular network. Clearly, from the description of the

%DROP, a decrease in the %DROP would be very

advantageous to the network, as the number of

abnormal disconnections would decrease.

The idle channel measurement (ICM) was also

used as an interference indicator. The idle channel

measurement (ICM) parameter is explained with the

use of figure 2. There are five interference bands,

each marked by a limit. For example, interference

band 1 ends at limit 1 and interference band 2 ends

at limit 2. This continues up to interference band 5,

which is the last interference band. The limits 1 to 5

are represented by the ICM parameters, namely

ICM1 to ICM5, respectively. The ICM band

parameters provide an indication of the level of

interference in the cell. A large number of points in

the ICM4 and ICM5 bands indicates a large amount

of interference in the BSC and is a very

unfavourable situation. From figure 2, it can be seen

that the more points in band 5, the more the

interference (~-47dBm), while interference band 1

has much less interference (~110dBm). Thus ICM5

is worse than ICM4 and similarly ICM4 is worse

than ICM3 and so on. The ideal situation in a mobile

cellular network BSC is to have all points located in

ICM1 and ICM2, a smaller number of points in

ICM3 and virtually no points in ICM4 and ICM5.

Figure 2: Interference bands 1 to 5, each interference band

ends at a limit.

7 RESULTS OF

IMPLEMENTATION INTO A

CELLULAR RADIO NETWORK

The frequency assignments produced by the SIMBA

took on average 24 hours to produce. The frequency

assignment produced by the SIMBA was

implemented in a cellular radio network. From

figure 3 it is clear that there was a decrease in the

%DROP on the BSC after the frequency assignment

solution was implemented. This can be seen by

studying the %DROP before and after the vertical

black broken line. The vertical black broken line

depicts the point at which the SIMBA frequency

assignment solution was implemented into the BSC.

Figure 3: %DROP before and after the SIMBA frequency

assignment solution was implemented.

The decrease in the %DROP was a substantial

0.2 in figure 3 on the %DROP scale. This may not

seem significant, but in terms of the %DROP on a

cellular network that prides itself on its low

%DROP, a decrease of 0.2 is amazing. An

improvement of 0.2 on the %DROP scale on a BSC

carrying a large amount of traffic can equate to a

large addition in revenue. To substantiate the actual

decrease of a 0.2 on the %DROP scale, the traffic

(erlang rate) would have to have remained constant,

since a decrease in the erlang rate would also cause a

decrease in the %DROP. However, by studying

figure 3 it can be seen that the erlang rate remained

constant while there was a distinct decrease in the

%DROP after the SIMBA frequency assignment

solution was implemented.

Figure 4 depicts the actual idle channel

measurements for the BSC before and after the

SIMBA frequency assignment solution was

implemented. Remember that the vertical black

broken line represents the point at which the

frequency assignments were implemented. It is

apparent from the measurements in figure 4 that

there was a drastic drop in ICM5 and ICM4

parameter values after the SIMBA frequency

assignment solution was implemented. There was

also an extensive improvement in ICM2 after the

implementation. These results prove that the SIMBA

frequency assignment solution has made

FREQUENCY ASSIGNMENT OPTIMIZATION USING THE SWARM INTELLIGENCE MULTI-AGENT BASED

ALGORITHM (SIMBA)

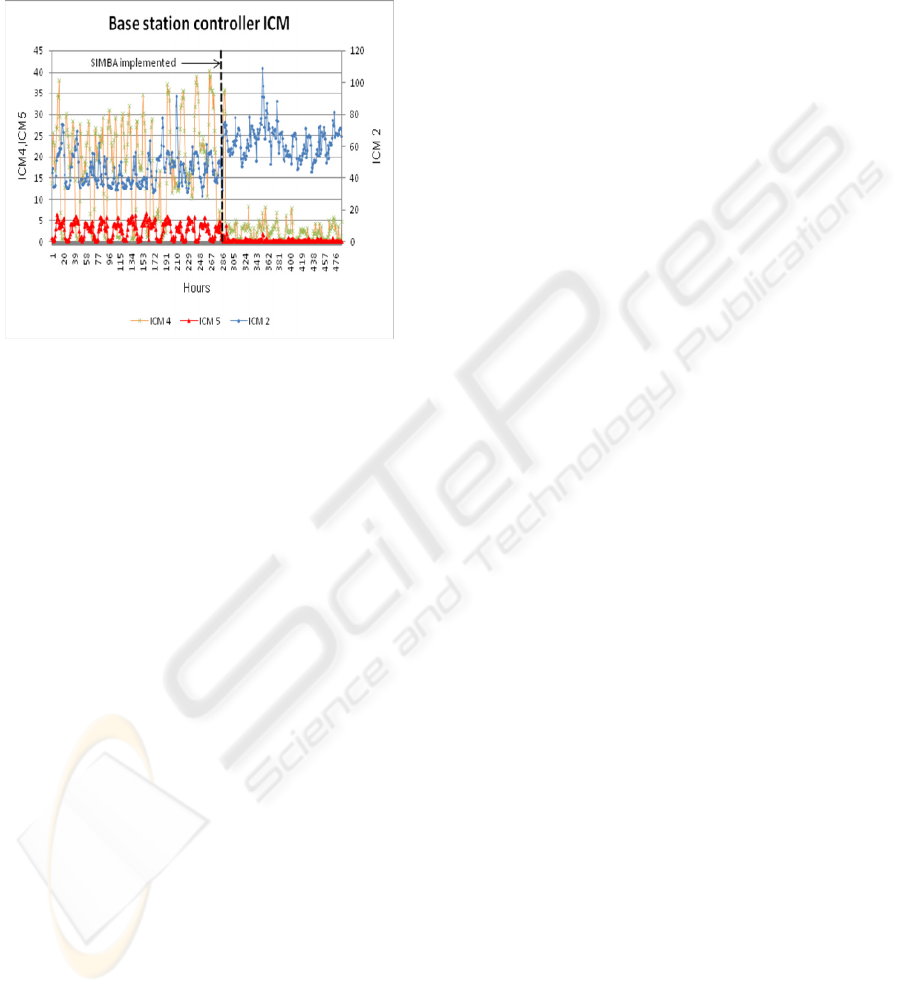
considerable improvements to the quality on the

BSC. The BSC was optimized to the ideal situation

with regard to the ideal channel measurements (see

section 6) as the number of points has decreased in

the ICM4 and ICM5 bands, while the ICM2 band

has increased considerably (see figure 4).

Figure 4: ICM interference bands 2, 4 and 5 before and

after the SIMBA frequency assignment solution was

implemented.

8 CONCLUSIONS

An engineering problem of high practical relevance

has been addressed in this paper. An algorithm based

on swarm intelligence that utilizes a multi-agent

system has been proposed. The SIMBA also

includes a stigmergy single cell optimization

(SSCO) approach which is used during selection of

the best frequencies that minimize interference

patterns. This approach has a strong analogy to

natural stigmergy in natural. One of the most

important characteristics of the SSCO was that

agents recognize interference patterns in the

changing structure of the frequency assignment

solution and are able to augment it with new

components that minimize the interference pattern.

The agents are able to make these decisions as the

changing configuration of the structures acts as a

source of information that aids the agents.

Another important aspect of the SIMBA was the

social model created by the multi-agent system.

Each agent was able to make local changes to its

own local knowledge; however the agent also could

gain addition knowledge from the collective giving

the SIMBA its swarm intelligence characteristics.

The SIMBA was benchmarked against the

COST 259 benchmarks, in particular the Siemens set

of problems and the SIMBA closely match some of

the best results with a search time of 24 hours. The

frequency assignment solutions produced by SIMBA

were also implemented into a commercial cellular

radio network with good results.

ACKNOWLEDGEMENTS

The authors wish to thank the University of

Johannesburg and the Academy for Information

Technology at the University of Johannesburg.

REFERENCES

Beckmann, D., Killat, U., 1999. Frequency Planning with

respect to Interference Minimization in Cellular Radio

Networks. TD(99)032, COST 259, Vienna, Austria,

January.

Bonabeau, E., Dorigo, M., Theraulaz, G., 1999. Swarm

Intelligence: From Natural to Artificial Systems (Santa

Fe Institute Studies in the Sciences of Complexity

Proceedings), Oxford University Press.

Eisenblätter A. and Koster A., 2008. FAP web page,

http://fap.zib.de

Hale, W.K., 1980. Frequency assignment: theory and

applications. Proc. IEEE, vol. 68, pp 1497-1514, Dec.

Hao J., Dorne R., Galinier P., 1998. Tabu Search for

Frequency Assignment in Mobile Radio Networks.

Journal of Heuristics, vol 4 pp 47-62.

Hellebrandt, H., and H. Heller, H., 2000. A new heuristic

method for frequency assignment. TD(00)003, COST

259, Valencia, Spain, January.

Kristensen, L.K., 2000. Aintz: Collective Problem Solving

by Artificial Ants.

http://www.evalife.dk/publications2.php

Mannino, C., Oriolo, G., Ricci, F., 2002. Solving Stability

Problems on a Superclass of Interval Graphs.

Universit'a di Roma La Sapienza, Dipartimento di

Informatica e Sistemistica, vol.26 no. 02.

Michalewicz, Z., Schmidt, M., Michalewicz, M., Chiriac,

C., 2007. Adaptive Business Intelligence. Springer.

Montemanni, R., Moon, J.N.J., Smith D.H., 2003. An

Improved Tabu Search Algorithm for the Fixed-

Spectrum Frequency Assignment Problem. IEEE

Transactions on Vehicular Technology, vol. 52, no. 3,

pp 891-901, May.

O’Reilly, G.B., and Ehlers E.M., 2008. The Swarm Effect

Minimization Algorithm. 10

International Conference

on Enterprise Information Systems (ICEIS),

Barcelona, Spain, June.

Valckenaers, P., Kollingbaum, M., van Brussel, H.,

Bochmann, O., and Zamfirescu, C., 2001. The Design

of Multi-Agent Coordination and Control Systems

using Stigmergy. Proc. of the IWES'01 Conference.

http://www.csd.abdn.ac.uk/~mkolling/publications/De

signMultiAgentCoordControlStigmergy.pdf

ICEIS 2009 - International Conference on Enterprise Information Systems