A NEW HEURISTIC FUNCTION IN ANT-MINER APPROACH

Urszula Boryczka and Jan Kozak

Institute of Computer Science, University of Silesia, Be¸dzi´nska 39, 41-200 Sosnowiec, Poland

Keywords:

Ant Miner, Ant Colony Optimization, Data Mining.

Abstract:

In this paper, a novel rule discovery system that utilizes the Ant Colony Optimization (ACO) is presented.

The ACO is a metaheuristic inspired by the behavior of real ants, where they search optimal solutions by

considering both local heuristic and previous knowledge, observed by pheromone changes. In our approach

we want to ensure the good performance of Ant-Miner by applying the new versions of heuristic functions in

a main rule. We want to emphasize the role of the heuristic function by analyzing the inﬂuence of different

propositions of these functions to the performance of Ant-Miner. The comparative study will be done using

the 5 data sets from the UCI Machine Learning repository.

1 INTRODUCTION

Data mining is a process of extracting useful knowl-

edge from real-world data. Among several data min-

ing tasks – such as clustering and classiﬁcation –

this paper focuses on classiﬁcation. The aim of the

classiﬁcation algorithm is to discover a set of clas-

siﬁcation rules. One algorithm for solving this task

is Ant-Miner, proposed by Parpinelli and colleagues

(Parpinelli et al., 2004), which employs ant colony

optimization techniques (Corne et al., 1999; Dorigo

and St¨utzle, 2004) to discoverclassiﬁcation rules. Ant

Colony Optimization is a branch of a newly developed

form of artiﬁcial intelligence called swarm intelli-

gence. Swarm intelligence is a form of emergent col-

lective intelligence of groups of simple individuals:

ants, termits or bees in which a form of indirect com-

munication via pheromone we observe. Pheromone

values encourage the following ants to build good so-

lutions of analyzed problem and the learning process

occurring in this situation is called positive feedback

or auto catalysis.

The application of ant colony algorithms to rule

induction and classiﬁcation is a research area still not

very good explored and tested. The appeal of this

approach similarly to the evolutionary techniques are

that they provide an effective mechanism for conduct-

ing a more global search. These approaches have

based on a collection of attribute-value terms, then

it can be expected that these approaches will also

cope better with attribute interaction than greedy in-

duction algorithms (Galea, 2002). What is more,

these applications require minimum understanding of

the problem domain; the main components are: the

heuristic function and an evaluation function, both of

which may be employed in ACO approach in the same

shapes as in existing literature, concerning determin-

istic rule induction algorithms.

Ant-Miner is an ant-based system and it is more

ﬂexible and robust than traditional approaches. The

application of ant colony algorithms to rule induc-

tion and classiﬁcation is a research area still not very

good explored and tested. This method incorpo-

rates a simple ant system in which a heuristic value

based on entropy measure is calculated. Ant-Miner

has produced good results when compared with more

conventional data mining algorithms, such as C4.5

(Quinlan, 1993), ID3 and CN2 (Clark and Boswell,

1991; Clark and Niblett, 1989), and it is still a rel-

atively recent algorithm, which motivates us trying

to amend it. This work proposes some modiﬁca-

tions to the Ant-Miner to improve it. In the origi-

nal Ant-Miner, the goal of the algorithm was to pro-

duce an ordered list of rules, which was then applied

to test data in order in which they were discovered.

Original Ant-Miner was compared to CN2 (Clark and

Boswell, 1991; Clark and Niblett, 1989), a classiﬁca-

tion rule discovery algorithm that uses a strategy for

generating rule sets similar to that of heuristic func-

tion used in main rule of ants’ strategy in Ant-Miner.

The comparison was done using 6 data sets from the

UCI Machine Learning repository that is accessible

Boryczka U. and Kozak J. (2009).

A NEW HEURISTIC FUNCTION IN ANT-MINER APPROACH.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

33-38

DOI: 10.5220/0001857700330038

 SciTePress

at www.ics.uci.edu/˜mlearn/MLRepository.html. The

results were analyzed according to the predictive ac-

curacy of the rule sets and the simplicity of the dis-

covered rule set, which is measured by the number of

terms per rule. While Ant-Miner had a better predic-

tive accuracy than CN2 on 4 of the data sets and a

worse one on only one of the data sets, the most in-

teresting result is that Ant-Miner returned much sim-

pler rules than CN2. Similar conclusions could also

be drawn from a comparison of Ant-Miner to C4.5, a

well-known decision tree algorithm (Quinlan, 1993).

Outline. This article is organized as follows. Sec-

tion 1 comprises an introduction to the subject of this

article. In section 2, Ant Colony Optimization in Rule

Induction is presented. Section 3 describes the modi-

ﬁcations and extensions of original Ant-Miner. In sec-

tion 4 our proposed modiﬁcations are shown. Then

the computational results performed in ﬁve tests are

reported. Finally, we conclude with general remarks

on this work and further directions for future research

are pointed out.

2 ANT COLONY OPTIMIZATION

IN RULE INDUCTION

The adaptation of ant colony optimization to rule in-

duction and classiﬁcation is a research area still not

good explored and examined. Ant-Miner is a se-

quential covering algorithm that merged concepts and

principles of ACO and rule induction. Starting from

a training set, Ant-Miner generates a set of ordered

rules through iteratively ﬁnding an appropriate rule,

that covers a subset of the training data, adds the for-

mulated rule to the induced rule list, and then removes

the examples covered by this rule as long as the stop-

ping criteria is reached.

ACO owns a number of features that are important

to computational problem solving (Freitas and John-

son, 2003):

• it is relatively simple and easy to understand and

then to implement

• it offers emergent complexity to deal with other

optimization techniques

• it is compatible with the current trend towards

greater decentralization in computing

• it is adaptive and robust and it is enable to cope

with noisy data.

There are many other characteristics of ACO which

are really importantin data mining applications. ACO

in contrary to deterministic decision trees or rule in-

duction algorithms during rule induction, tries to ex-

tenuate this problem of premature convergence to

local optima because of stochastic element which

prefers a global search in the problem’s search space.

Secondly, ACO metaheuristics is a population–based

one. It permits the system to search in many indepen-

dently determined points in the search space concur-

rently and to use the positive feedback between ants

as a search mechanism (Parpinelli et al., 2002).

Ant-Miner was invented by Parpinelli et al.

(Parpinelli et al., 2004; Parpinelli et al., 2002). It was

the ﬁrst Ant algorithm for rule induction and it has

been shown to be robust and comparable with CN2

(Clark and Boswell, 1991) and C4.5 (Quinlan, 1993)

algorithms for classiﬁcation. Ant-Miner generates so-

lutions in the form of classiﬁcation rules. Original

Ant–Miner has a limitation that it can only process

discrete values of attributes.

Algorithm 1: Algorithm Ant-Miner.

TrainingSet =

{

all training examples

};

DiscoveredRuleList = [ ]

; /* rule list is initialized with

an empty list */

while

(TrainingSet > MaxUncoveredExamples)

t = 1

; /* ant index */

j = 1

; /* convergence test index */

Initialize all trails with the same amount

of pheromone

;

repeat

Ant

starts with an empty rule and

incrementally constructs a

classification rule

by adding one

term at a time to the current rule

;

Prune rule

R−t;

Update the pheromone amount of all

trails by increasing pheromone in the

trail followed by

Ant

(proportional to

the quality of

) and decreasing

pheromone amount in the other trails

(simulating pheromone evaporation)

;

/* update convergence test */

(

is equal to

− 1

)

then

j = j + 1

;

else

j = 1

;

end if

t = t + 1

;

until

(

t ≥

No of ants) OR

(

j ≥

No rules converg)

;

Choose the best rule

best

among all rules

constructed by all the ants

;

Add rule

best

to DiscoveredRuleList

;

TrainingSet = TrainingSet - (set of

examples correctly covered by

best

)

;

end while

ICEIS 2009 - International Conference on Enterprise Information Systems

A short review of the main aspects of the rule dis-

covery process by Ant-Miner is run parallel to the

description of Ant-Miner algorithm. Ant-Miner pro-

duces a sequential covering approach to discover a

list of classiﬁcation rules, by discovering one rule at a

time until all or almost all the examples in the training

set are covered by the discovered rules.

All cells in the pheromone table are initialized

equally to the following value:

(t = 0) =

∑

i=1

where:

• a – the total number of attributes,

• b

– the number of values in the domain of at-

tribute i.

The probability is calculated for all of the

attribute–value pairs, and the one with the highest

probability is added to the rule. The transition rule

in Ant-Miner is given by the following equation:

(t) · η

∑

(t) · η

, ∀i ∈ I

where:

• η

is a problem-dependent heuristic value for

each term,

• τ

is the amount of pheromone currently available

at time t on the connection between attribute i and

value j,

• I is the set of attributes that are not yet used by the

ant,

• Parameter β is equal to 1.

In Ant-Miner, the heuristic value is supposed to

be an information theoretic measure for the quality of

the term to be added to the rule. For preferring the

quality is measured in terms of entropy this term to

the others, and the measure is given as follows:

log

(k) − InfoT

∑

(log

(k) − InfoT

)

where the function Info is similar to another function

employed in C4.5 approach:

In foT

= −

∑

w=1



freqT



log



freqT



(1)

where: k is the number of classes, |T

| is the total

number of cases in partition T

(the partition contain-

ing the cases, where attribute A

has the value V

freqT

is the number of cases in partition T

with

class w, b

is a number of values in the domain of

attribute A

(a is the total number of attributes). The

higher the value of InfoT

is, the less likely is that the

ant will choose term

to add to its partial rule. Please

note that this heuristic function is a local method and

it is sensitive to attribute interaction. The pheromone

values assigned to the term have a more global na-

ture. The pheromone updates depend on the evalua-

tion of a rule as a whole, i.e. we must take into ac-

count interaction among attributes appearing in the

rule. The heuristic function employed here comes

from the decision tree world and it is similar to the

method used in algorithm C4.5. There are many other

heuristic functions that may can adapted and used in

Ant-Miner. We can derivethem from information the-

ory, distance measures or dependence measures.

The rule pruning procedure iteratively removes

the term whose removal will cause the maximum

increase in the quality of the rule. The quality of a

rule is measured using the following formula:

Q =



TruePos

TruePos+ FalseNeg





TrueNeg

FalsePos+ TrueNeg



where:

• TruePos - the number of cases covered by the rule

and having the same class as the one predicted by

the rule,

• FalsePos - the number of cases covered by the rule

and having a different class from the one predicted

by the rule,

• FalseNeg - the number of cases that are not cov-

ered by the rule while having a class predicted by

the rule,

• TrueNeg - the number of cases that are not cov-

ered by the rule which have a different class from

the class predicted by the rule.

The quality measure of a rule is determined by:

Q = sensitivity· specificity.

We can say that accuracy among positive instances

determines sensitivity, and the accuracy among neg-

ative instances determines speciﬁcity. Now we take

into account only the rule accuracy, but it can be

changed to analyze the rule length and interesting-

ness.

Once each ant completes the construction of the

rule, pheromone updating is carried out as follows:

(t + 1) = τ

(t) + τ

(t) · Q, ∀term

∈ the rule

The amount of the pheromones of terms belonging

to the constructed rule R are increased in proportion to

the quality of Q. To simulate pheromone evaporation

, the amount of pheromone associated with each

A NEW HEURISTIC FUNCTION IN ANT-MINER APPROACH

term

which does not occur in the constructed rule

must be decreased. The reduction of pheromone of

an unused term is performed by dividing the value of

each τ

by the summation of all τ

. The pheromone

levels of all terms are then normalized.

3 FIRST MODIFICATIONS

The authors of Ant-Miner (Parpinelli et al., 2004;

Parpinelli et al., 2002) suggested two directions for

future research:

1. Extension of Ant-Miner to cope with continuous

attributes;

2. The investigation of the effects of changes in the

main transition rule:

(a) the local heuristic function,

(b) the pheromone updating strategies.

Recently, Galea (Galea and Shen, 2006) proposed

a few modiﬁcations in Ant-Miner. Another modi-

ﬁcations (Oakes, 2004; Martens et al., 2006) cope

with the problem of attributes having ordered cate-

gorical values, some of them improve the ﬂexibility

of the rule representation language. Finally, more so-

phisticated modiﬁcations have been proposed to dis-

cover multi-label classiﬁcation rules (Chan and Fre-

itas, 2006) and to investigate fuzzy classiﬁcation rules

(Galea and Shen, 2006). Certainly there are still many

problems and open questions for future research.

3.1 Data Sets used in our Experiments

The evaluation of the performance behavior of dif-

ferent modiﬁcations of Ant-Miner was performed us-

ing 5 public-domain data sets from the UCI.Please

note that Ant-Miner cannot cope directly with contin-

uous attributes (i.e. continuous attributes have to be

discretized in a preprocessing step, using the RSES

program (logic.mimuw.edu.pl/˜rses/)). In the original

Ant-Miner and Galea implementation (Galea, 2002),

the discretization was carried out using a method

called C4.5-Disc (Kohavi and Sahami, 1996). C4.5-

Disc is an entropy-based method that applies the

decision-tree algorithm C4.5 to obtain discretization

of the continuous attributes.

Both the original Ant-Miner and our proposal

have some parameters. The ﬁrst one – the number

of ants will be examined during the experiments.

4 PROPOSED MODIFICATIONS

An Ant Colony Optimization technique is in essence,

a system based on agents which simulate the natural

behavior of ants, incorporating a mechanism of co-

operation and adaptation, especially via pheromone

updates. When solving different problems with the

ACO algorithm we have to analyze three major func-

tions. Choosing these functions appropriately helps

to create better results and prevents stacking in local

optima of the search space.

The ﬁrst function is a problem-dependentheuristic

function (η) which measures the quality of terms that

can be added to the current partial rule. The heuris-

tic function stays unchanged during the algorithm run

in the classical approach. We want to investigate

whether the heuristic function depends on the previ-

ous well-known approaches in the data-mining area

(C4.5, CART, CN2) and can inﬂuence the behavior of

the whole colony,or not. According to the proposition

concerning the heuristic function (Liu et al., 2004),

we also analyze the simplicity of this part of a main

transition rule in Ant-Miner. The motivation is as fol-

lows: in ACO approaches we do not need sophisti-

cated information in the heuristic function, because of

the pheromone value, which compensates some mis-

takes in term selections. Our intention is to explore

the effect of using a simpler heuristic function instead

of a complex one, originally proposed by Parpinelli

(Parpinelli et al., 2004), so we change the formula

presented in the formula 1.

4.1 CART Inﬂuences

In the case of a method CART proposed by (Breiman

et al., 1984), the value of InfoT

is determined ac-

cording to the following formula 2.

In foT

= 2· P

· P

∑

w=1

|Pw

− Pw

| (2)

where:

• P

– a ratio of a number of objects in which the

speciﬁc attribute i has a value j to all objects in a

testable data set,

• P

– a ratio of a number of objects in which the

speciﬁc attribute i has not an analyzed value j to

all objects in a testable data set,

• Pw

– a ratio of a subset of objects belonging to

the decision class w in which the speciﬁc attribute

i has a value j to all objects having the value j,

• Pw

– the ratio of a subset of objects belonging

to the decision class w in which the speciﬁc at-

tribute i has not a value j to all objects having the

value j.

ICEIS 2009 - International Conference on Enterprise Information Systems

4.2 CN2 Inﬂuences

In the case of a method CN2 proposed by (Clark and

Boswell, 1991; Clark and Niblett, 1989), the value of

InfoT

is calculated in the formula 3 (according the

Laplace error estimate):

In foT

= argmax



fregT

+ 1

| + k



(3)

where w is a speciﬁc decision class, range from 1 to k.

4.3 Mixture of Modiﬁcations

Mixed methods proposed to determine the InfoT

values make use of early presented rules (early pro-

posed C4.5, CART and CN2 inﬂuences). These

mechanisms are used after the rule construction, al-

ternately.

Experiments in this part of experimental study

will be performed with a combination of following

modiﬁcations: C4.5 + CART, C4.5 + CART + CN2,

CART + CN2, C4.5 + CN2.

4.4 Results

For each experimental study the number of ants was

established experimentally, separately for each of the

testable data sets. For each data set we execute 100

times per experiment. Seven different modiﬁcations

are analyzed separately for each testable data set.

4.4.1 Breast Cancer Data Set

In this experimental study we want to see whether the

changeable method of calculation the InfoT

has an

effect on the better performance in this case. Table

1 shows the results for 5 ants employed in this ex-

periment with Breast cancer data set. The better re-

sults concerning the predictive accuracy (1,73%) and

smaller values in the case of standard deviations.

4.4.2 Wisconsin Breast Cancer Data Set

From the study for Wisconsin breast cancer we ob-

serve the similar results as in a classical approach. We

consider only one ant as a population size. The better

results we can ﬁnd in the case of separate C4.5 modi-

ﬁcation and the mixture of C4.5, CART and CN2 (the

smaller value of standard deviations).

4.4.3 Dermatology Data Set

According to the proposition concerning different

heuristic functions, we also analyzed the same effect

in Dermatology data set as in previous one. Our in-

vestigation performed 40 ants and the predictive ac-

curacy has the higher value for C4.5, CN2 and CART

mixture of modiﬁcations. Slightly worth results we

obtain in case of C4.5 approach (0,04%). In general,

this data set is more resistant than the others in the

context of effectiveness of our approaches. It can be

seen that these modiﬁcations are similar to the origi-

nal Ant-Miner approach in the context of accuracy.

4.4.4 Hepatitis Data Set

In the case of Hepatitis data set the analyzed modiﬁca-

tions are slightly different from the Ant-Miner imple-

mentation. The standard deviations are higher than in

other experiments. It is especially interesting that for

Breast cancer and Hepatitis, the algorithms achieved

the worse effectiveness. On contrary, in the case of

Wisconsin data set we observe the good performance

for all analyzed modiﬁcations. The best performance

we observe in the mixture of C4.5 and CART ap-

proaches (only 0,27%).

4.4.5 Tic-tac-toe Data Set

We also observe a diminishing value of the accuracy

in the case of Tic-tac-toe data set. In this situation,

the question arises as to whether the loss of accuracy

is due to the incorrect methodology or to the speciﬁc

difﬁculty in the process of classiﬁcation.

We also observed not very promising performance

in this experimental study.

Table 1 shows the accuracy and standard devia-

tions for rule sets produced in different approaches.

It can be seen that in general these modiﬁcations are

similar to the original Ant-Miner in the context of ef-

fectiveness. It can be intriguing aspect for future re-

search to adjust speciﬁc features of data sets to the

nature of methods used as a heuristic functions.

5 CONCLUSIONS

In this paper we examined different modiﬁcations

concerning the heuristic function in Ant-Miner ap-

proach. The proposed modiﬁcations were simulated

and compared for different data sets. The results

showed that the proposed modiﬁcations were similar

to the classical approach and they can preserve high

value of predictive accuracy.

Finally, a lot of research works is still remain-

ing in order to ﬁnd a good strategy for matching the

special heuristic function to the speciﬁc features of

a data structure. We plan in the future to evaluate

A NEW HEURISTIC FUNCTION IN ANT-MINER APPROACH

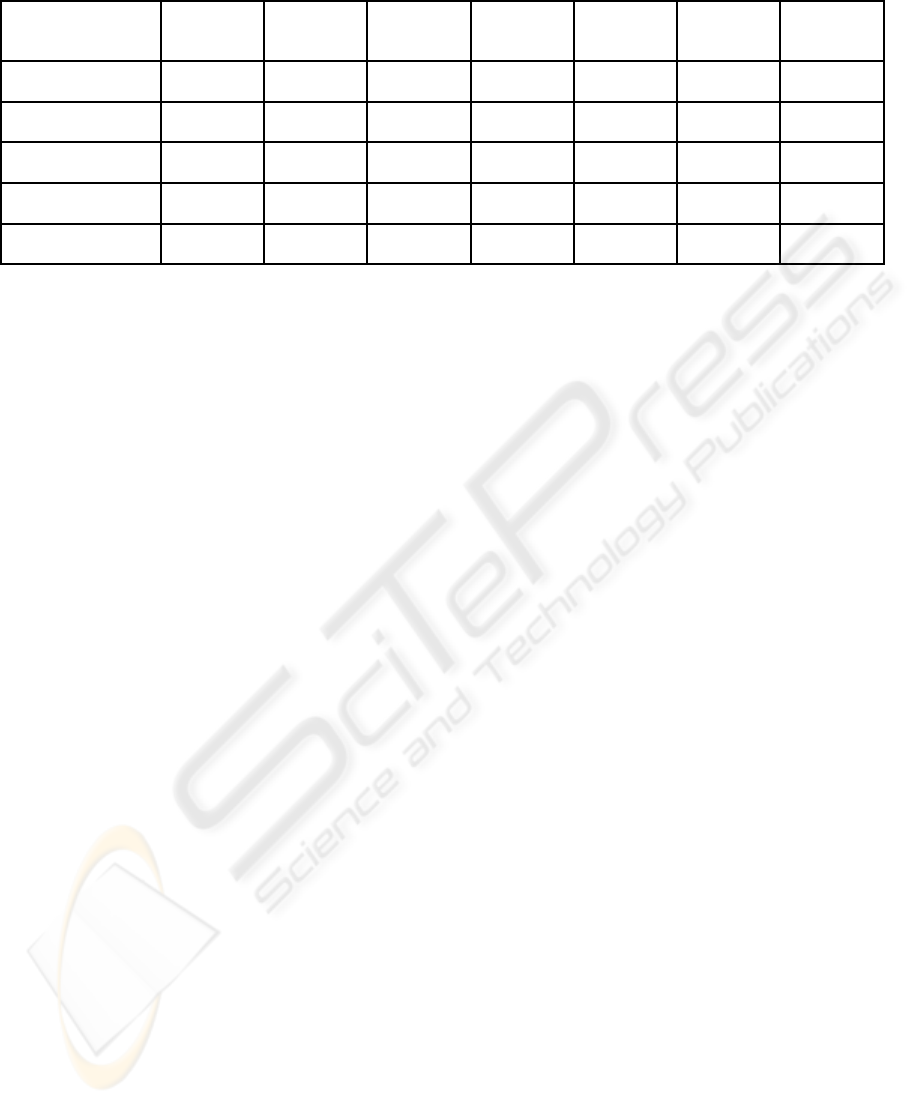
Table 1: Comparative study. Accuracy of classiﬁcation and standard deviation %.

Dataset Standard

(C4.5)

CART CN2 C4.5 +

CART

C4.5 +

CART +

CN2

CART +

CN2

C4.5 +

CN2

Breast cancer 72.07

(± 3.41)

71.98

(± 2.19)

72.11

(± 2.62)

73.80

(± 2.34)

73.59

(± 2.27)

71.78

(± 2.52)

73.60

(± 2.41)

Wisconsin breast

cancer

92.15

(± 1.11)

91.80

(± 0.90)

91.78

(± 1.11)

91.69

(± 1.38)

92.16

(± 0.88)

91.69

(± 1.06)

91.71

(± 1.07)

Dermatology 93.75

(± 1.29)

93.86

(± 1.32)

93.62

(± 1.70)

93.37

(± 1.67)

93.90

(± 1.43)

93.79

(± 1.41)

93.83

(± 1.76)

Hepatitis 77.98

(± 2.97)

77.34

(± 2.86)

76.09

(± 3.45)

78.25

(± 2.79)

77.90

(± 2.93)

76.58

(± 2.72)

77.81

(± 2.66)

Tic-tac-toe 73.90

(± 1.81)

72.45

(± 1.91)

71.69

(± 1.81)

73.77

(± 1.87)

74.06

(± 1.89)

72.02

(± 1.77)

73.55

(± 1.78)

Ant-Miner modiﬁcations with large data sets and with

several new modiﬁcations to better validation of our

approach.

REFERENCES

Breiman, L., Friedman, J. H., Olshen, R. A., and Stone, C. J.

(1984). Classiﬁcation and Regression Trees. Belmont

C.A., Wadsworth.

Chan, A. and Freitas, A. A. (2006). A new ant colony algo-

rithm for multi-label alssiﬁcation with applications in

bioinformatics. In Proceedings of Genetic and Evo-

lutionary Computation Conf. (GECCO’ 2006), pages

27–34, San Francisco.

Clark, P. and Boswell, R. (1991). Rule induction with CN2:

some recent improvements. In Proc. European Work-

ing Session on Learning (EWSL-91), pages 151–163,

Berlin. Springer Verlag, LNAI 482.

Clark, P. and Niblett, T. (1989). The CN2 rule induction

algorithm. Machine Learning, 3(4):261–283.

Corne, D., Dorigo, M., and Glover, F. (1999). New Ideas in

Optimization. Mc Graw–Hill, Cambridge.

Dorigo, M. and St¨utzle, T. (2004). Ant Colony Optimiza-

tion. MIT Press, Cambridge.

Freitas, A. A. and Johnson, C. G. (2003). Research cluster

in swarm intelligence. Technical Report EPSRC Re-

search Proposal GR/S63274/01 — Case for Support,

Computing Laboratory, Laboratory of Kent, Kent.

Galea, M. (2002). Applying swarm intelligence to rule in-

duction. Master’s thesis, MS thesis, University of Ed-

ingbourgh.

Galea, M. and Shen, Q. (2006). Simultaneous ant colony

optimization algorithms for learning linguistic fuzzy

rules. In Agraham, A., Grosan, C., and Ramos, V.,

editors, Swarm Intelligence in Data Mining. Springer,

Berlin.

Kohavi, R. and Sahami, M. (1996). Error-based and

entropy-based discretization of continuous features.

In Proc. 2nd Intern. Conference Knowledge Discov-

ery and Data Mining, pages 114–119.

Liu, B., Abbas, H. A., and Kay, B. M. (2004). Classiﬁcation

rule discovery with ant colony optimization. IEEE

Computational Intelligence Bulletin, 1(3):31–35.

Martens, D., Backer, M. D., Haesen, R., Baesens, B., and

Holvoet, T. (2006). Ants constructing rule-based clas-

siﬁers. In Agraham, A., Grosan, C., and Ramos, V.,

editors, Swarm Intelligence in Data Mining. Springer,

Berlin.

Oakes, M. P. (2004). Ant colony optimization for stylom-

etry: the federalist papers. In Proceedings of Recent

Advances in Soft Computing (RASC — 2004), pages

86–91.

Parpinelli, R. S., Lopes, H. S., and Freitas, A. A. (2002).

An ant colony algorithm for classiﬁcation rule discov-

ery. In Abbas, H., Sarker, R., and Newton, C., editors,

Data Mining: a Heuristic Approach. Idea Group Pub-

lishing, London.

Parpinelli, R. S., Lopes, H. S., and Freitas, A. A. (2004).

Data mining with an ant colony optimization algo-

rithm. IEEE Transactions on Evolutionary Com-

putation, Special issue on Ant Colony Algorithms,

6(4):321–332.

Quinlan, J. R. (1993). C4.5: Programs for Machine Learn-

ing. Morgan Kaufmann, San Francisco.

ICEIS 2009 - International Conference on Enterprise Information Systems