DIRECTED ACYCLIC GRAPHS AND DISJOINT CHAINS

Yangjun Chen

Dept. Applied Computer Science, University of Winnipeg, Canada

Keywords: Graphs, DAGs, Chains, Paths, Transitive Closure, Reachability Queries.

Abstract: The problem of decomposing a DAG (directed acyclic graph) into a set of disjoint chains has many

applications in data engineering. One of them is the compression of transitive closures to support

reachability queries on whether a given node v in a directed graph G is reachable from another node u

through a path in G. Recently, an interesting algorithm is proposed by Chen et al. (Y. Chen and Y. Chen,

2008) which claims to be able to decompose G into a minimal set of disjoint chains in O(n

+ bn

) time,

where n is the number of the nodes of G, and b is G’s width, defined to be the size of a largest node subset

U of G such that for every pair of nodes u, v ∈ U, there does not exist a path from u to v or from v to u.

However, in some cases, it fails to do so. In this paper, we analyze this algorithm and show the problem.

More importantly, a new algorithm is discussed, which can always find a minimal set of disjoint chains in

the same time complexity as Chen’s.

1 INTRODUCTION

Given a DAG G(V, E) (directed acyclic graph) with

|V| = n and |E| = e, we want to decompose it into a

minimal set of disjoint chains such that any node in

G appears on some chain, and on each chain, if node

v appears above node u, there is a path from v to u in

This problem is important to compressing a

transitive closure (Wang

et al. , 2006; Warshall, 1962)

to support reachability queries, by which we will

check whether a given node v in G is reachable from

another node u through a path in G (Cohen, 1991;

Cohen

et al., 2003; Cheng et al., 2006; Jagadish,

1990; Schenkel

et al., 2006; Teuhola, 1996; Zibin et

al.

, 2001), which has a wide range of applications.

For example, in object-oriented databases, graph

reachability is important in managing class

inheritance hierarchies.

As an example, consider a graph G shown in Fig.

1(a). Its transitive closure is shown in Fig. 1(b). It

can be stored as a 0-1 matrix as shown in Fig. 1(c)

with O(n

) space requirement.

Assume that we can decompose G into a set of

disjoint chains as shown in Fig. 2(a). Then, we can

assign each node an index as follows:

(1) Number each chain and number each node on a

chain.

(2) The jth node on the ith chain will be assigned a

pair (i, j) as its index.

Figure 1: DAG, transitive closure and 0-1 matrix.

In addition, each node v on the ith chain will be

associated with an index sequence of length k - 1: (1,

) … (i – 1, j

- 1) (i + 1, j

+ 1) … (k, j

) such that

any node with index (x, y) is a descendant of v if x =

i and y > j or x ≠ i but y ≥ j

, where k is the number

of the disjoint chains. In this way, the space over-

head is decreased to O(kn) (see Fig. 2(a) for

illustration). Especially, we can also store all the

index sequences as a n × k matrix M, in which each

entry M(v, j) is the j-th element in the index

sequence associated with node v. See Fig. 2(b) for

(b)

a b c d e f g h i

1 1 1 1 1 0 0 0 0

0 1 1 1 1 0 0 0 1

0 0 1 1 1 0 0 0 1

0 0 0 1 0 0 0 0 0

0 0 0 0 1 0 0 0 0

0 1 1 1 1 1 0 0 1

0 0 0 1 1 0 1 1 1

0 0 0 0 1 0 0 1 1

0 0 0 0 0 0 0 0 1

(c)

•

(a)

•

(b)

Chen Y. (2009).

DIRECTED ACYCLIC GRAPHS AND DISJOINT CHAINS.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages 17-24

DOI: 10.5220/0001858300170024

 SciTePress

illustration. So, a reachability checking needs only

O(1) time.

Figure 2: Graph encoding.

Note that the above method can also be used for

cyclic graphs (graphs containing cycles) since we

can always transform a cyclic graph to a DAG by

identifying all the strongly connected components

(SCCs) and then collapse each of them into a

representative node. Clearly, all of the nodes in an

SCC is equivalent to its representative as far as

reachability is concerned (Wang

et al., 2006). Using

Tarjan’s algorithm (Tarjan, 1972), all SCCs in G can

be found in O(n + e) time.

This idea was first suggested by Jagadish

(Jagadish, 1991). However, his algorithm needs

O(n

) time to decompose a DAG into a minimal set

of disjoint chains (see page 566 in Jagadish, 1991).

For this reason, Jagadish suggested a heuristic

method to decompose a DAG into a set of paths and

then stitch some paths together to form a chain. In

doing so, the number of the produced chains is

normally much larger than the minimum number of

chains, increasing significantly both space and query

time.

In (Y. Chen and Y. Chen, 2008), Chen discussed

a new algorithm to do the task. It requires only O(n

+ bn

) time, where b is the DAG’s width, defined

to be the size of a largest subset of pairwise unreach-

able nodes. Unfortunately, in some cases, the chain

set found using Chen’s algorithm is not always

minimum.

In this paper, we propose a new algorithm to

decompose a DAG into a minimal set of disjoint

chains. The time complexity of the new algorithm is

still bounded by

O(n

+ bn

The rest of the paper is organized as follows. In

Section 2, we present our algorithm in detail. Then,

in Section 3, we analyze the time complexity.

Finally, a short conclusion is set forth in Section 4.

2 ALGORITHM DESCRIPTION

In this section, we give our new algorithm, which is

inspired by Chen’s algorithm. However, to remove

the problem in Chen’s algorithm, we devise two new

procedures for generating chains and resolving

virtual nodes, respectively.

First, for the chain generation, we distinguish

between two kinds of virtual nodes and handle them

in different ways so that the reachability between

nodes can be transferred bottom-up by using such

virtual nodes.

Second, for the virtual node resolution, a new

data structure, the so-called combined alternating

graph, is constructed so that the number of virtual

nodes resolved at each level is maximized.

In the following, we first discuss how a DAG

can be decomposed into disjoint chains which may

contain virtual nodes in 2.1. Then, in 2.2, we show

how the virtual nodes can be resolved.

2.1 DAG Stratification and Chain

Generation

As with Chen’s algorithm, our algorithm works in

three phases: DAG stratification, chain generation,

and virtual node resolution.

In the first phase, a DAG G(V, E) is stratified

into several levels V

, ..., V

h-1

such that V = V

∪ ...

∪ V

h-1

and each node in V

has its children appearing

only in V

i-1

, ..., V

(i = 2, ..., h), where h is the height

of G, i.e., the length of the longest path in G. For

each node v in V

, its level is said to be i, denoted l(v)

= i. In addition, C

(v) (j < i) represents a set of links

with each pointing to one of v’s children, which

appears in V

. Therefore, for each v in V

, there exist

, ..., i

< i, l = 1, ..., k) such that the set of its

children equals

)(

∪ ... ∪

)(vC

. Assume that

= {v

, v

, ..., v

}. We use

(v) (j < i) to represent

) ∪ ... ∪ C

This phase is almost the same as Chen’s. But for

each node v at a level, we also use B

(v) to represent

a set of links with each pointing to one of v’s

parents, which appears in V

In the second phase, a series of (undirected)

bipartite graphs (Asrtian

et al., 1998; Hopcroft et al.,

1973) will be constructed. In this process, some

virtual nodes may be introduced into the levels V

= 1, ..., h - 2). Especially, we distinguish between

two kinds of virtual nodes. One is the virtual nodes

created for actual nodes; and the other is the virtual

nodes generated for virtual nodes. They will be

handled differently.

•

(1 1)

(2 2)(3 3)

(1 2)

(2 _3)(3, _)

(1, 3)

(2, _)(3, _)

•

(2, 1)

(1, 2)(3, 3)

(2, 2)

(1, 2)(3, 3)

(2, 3)

(1, _)(3, _)

•

(3, 1)

(1, _)(2, 3)

(3, 2)

(

1, 3

)(

(3, 3)

(_, _)(2, _)

1 2 3

2 2 3

2 3 -

- 3 -

3 - -

2 1 3

- 3 1

3 - 1

- - 3

a chain

(a) (b)

ICEIS 2009 - International Conference on Enterprise Information Systems

In the following, we begin our discussion with a

summarization of some important concepts related

to bipartite graphs, which are needed to define

virtual nodes.

Definition 1. (concepts related to matching, Asrtian

et al., 1998) Let G(V, E) be a bipartite graph. Let M

be a maximum matching of G. A node v is said to be

covered by M, if some edge of M is incident to v.

We will also call an uncovered node free. A path or

cycle is alternating, relative to M, if its edges are

alternately in E\M and M. A path is an augmenting

path if it is an alternating path with free origin and

terminus.

In addition, it is well known that using the

Hopcroft-Karp algorithm (Hopcroft

et al., 1973) a

maximum matching of G can be found in

O(|E|

||V

) time.

Also, the following symbols are used for ease of

explanation:

’ = V

∪ {virtual nodes introduced into V

= (v) ∪ {all the new edges from the nodes in V

to the virtual nodes introduced into V

i-1

}

G(V

, V

i-1

’; C

) - the bipartite graph containing V

and

i-1

’.

Definition 2. (virtual nodes for actual nodes) Let

G(V, E) be a DAG, divided into V

, ..., V

h-1

(i.e., V =

∪ ... ∪ V

h-1

). Let M

be a maximum matching of

the bipartite graph G(V

, V

i-1

’; C

) and v be a free

actual node (in V

i-1

’) relative to M

(i = 1, ..., h - 1).

Add a virtual node v’ into V

. In addition, for each

node u ∈ V

i+1

, a new edge u → v’ will be created if

one of the following two conditions is satisfied:

1. u → v ∈ E; or

2. There exists an edge (v

, v

) covered by M

such

that v

and v are connected through an alternating

path relative to M

; and u ∈ B

i+1

) or u ∈

i+1

v is called the source of v’, denoted s(v’).

A virtual edge from v’ to v is also generated to

indicate the relationship between v and v’. Besides, a

new edge u → v’ will be marked with ‘directly

connectable’ if one of the following conditions are

satisfied:

1. u → v ∈ E; or

2. There is an alternating path of length 1, which

connects v

and v. That is, v

→ v ∈ E.

We mark these edges with ‘directly connectable’

because it is possible for us to directly connect u and

v to remove v’.

The following example helps for illustration.

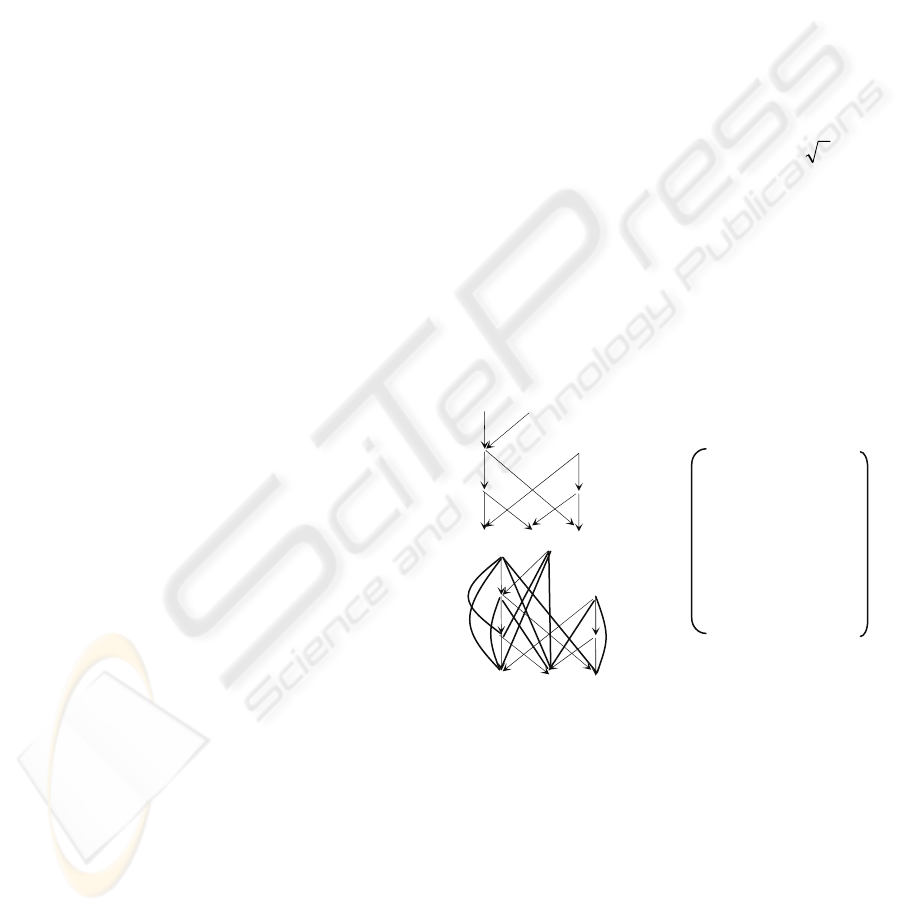
Example 1. Consider the graph shown in Fig. 3(a).

It can be divided into three levels as shown in Fig.

3(b). The bipartite graph made up of V

and V

G(V

, V

; C

), is shown in Fig. 3(c) and a possible

maximum matching M

of it is shown in Fig. 3(d).

Figure 3: A bipartite graph and a maximum matching.

Relative to M

, we have two free nodes i and a. For

them, two virtual nodes i’ and a’ will be constructed.

Then, V

’ = {b, e, h, i’, a’}. In addition, four new

edges (d, i’), (d, a’), (g, i’), and (g, a’) will be

constructed. But all of them will not be marked with

‘directly connectable’.

The motivation of constructing such a virtual

node (e.g., i’) is that it is possible to connect f to d or

g to form part of a chain if we transfer the edges on

an alternating path: b → c → e → f (see Fig. 3(e),

where a solid edge represents an edge belonging to

while a dashed edge to C

), or h → j → b → c

→ e → f. Then, we can connect d or g to f, as well as

b or h to i without increasing the number of chains,

as illustrated in Fig. 3(f). This can be achieved by

the virtual node resolution process (see 2.2).

For the graph shown in Fig. 4(a), which is the

second bipartite graph established for the graph

shown in Fig. 3.4(a), a possible maximum matching

is shown in Fig. 4(b). So M

∪ M

is a set of

chains as shown in Fig. 4(c)

Definition 3. (virtual nodes for virtual nodes) Let M

be a maximum matching of the bipartite graph G(V

i-1

’; C

) and v’ be a free virtual node (in V

i-1

’)

relative to M

(i = 1, ..., h - 1). Add a virtual node v’’

into V

. Set s(v’’) to be w = s(v’). Let l(w) = j. For

each node u ∈ V

i+1

, a new edge u → v’ will be

created if there exists an edge (v

, v

) covered by

j+1

such that v

and w are connected through an

alternating path relative to M

j+1

; and u ∈ B

i+1

) or u

∈ B

i+1

Again, a virtual edge from v’’ to v’ will be

generated to facilitate the virtual node resolution

process.

(a)

ac i

b h

(b)

(e) (f)

DIRECTED ACYCLIC GRAPHS AND DISJOINT CHAINS

Figure 4: A bipartite graph and a maximum matching.

Example 2. Consider the graph shown in Fig. 5(a).

Figure 5: Illustration for virtual nodes.

This graph can be divided into four levels as

shown in Fig. 5(b). The first bipartite graph

consisting of V

and V

, G(V

, V

; C

), is shown in

Fig. 5(c) and a possible maximum matching M

of it

is shown in Fig. 5(d). Relative to M

, we have a free

node f. For it, a virtual nodes f’ will be constructed.

Then, V

’ = {b, f’, d, h} (see Fig. 5(e)). Assume that

the maximum matching found for G(V

, V

’; C

) is

as shown in Fig. 5(f). A virtual node f’’ for f’ will be

established. So V

’ = {f’’, e, g}. Especially, we are

able to connect node f’’ and node p for the following

reason:

i) s(f’’) = s(f’) = f;

ii) (b, c) ∈ M

;

iii) f is connected to b through an alternating path: f

→ b; and

iv) p ∈ B

(c).

The corresponding bipartite graph G(V

, V

’; C

)

is shown in Fig. 5(g). The unique maximum

matching of G(V

, V

’; C

) is shown in Fig. 5(h).

By unifying M

, M

, and M

, we get a set of disjoint

chains as shown in Fig. 6(a).

Figure 6: Illustration for disjoint chains.

2.2 Virtual Node Resolution

In the third phase, we will remove all the virtual

nodes. This will be done top-down level by level;

and at each level any virtual node, which does not

have a parent along a chain, will be simply

eliminated. In addition, we call a virtual node v’ a

transit virtual node if one of the following two

conditions is satisfied.

1. Let u, v’, w be three consecutive nodes on a chain.

u → v’ is a marked edge (i.e., a directly

connectable edge); or

2. w is a virtual node.

In both cases, we connect u and w and then

remove v’. It is because in case (1), both u and w are

actual nodes and we have u → w ∈ E or there exists

a actual node x such that u → x ∈ E and x → w ∈ E.

In case (2), w is a virtual node, working as a

‘transfer’ of reachability.

For example, since node f’ in Fig. 6(a) is a

virtual node, node f’’ is a transit virtual node. It can

be directly removed, leading to a set of chains as

shown in Fig. 6(b). But node f’ cannot be removed

in this way since it is not a transit virtual node.

In the following, we discuss how to resolve a non-

transit virtual node, for which more effort is needed.

First, we define a new concept.

Definition 4. (alternating graph) Let M

be a

maximum matching of G(V

, V

i-1

’; C

). The

alternating graph

with respect to M

is a directed

graph with the following sets of nodes and edges:

) = V

∪ V

i-1

’, and

) = {u → v | u ∈ V

i-1

’, v ∈ Vi, and (u, v) ∈ M

}

∪ {v → u | u ∈ V

i-1

’, v ∈ V

, and (u, v) ∈ C

Example 3. Consider the graph shown in Fig. 3(a)

once again. Relative to M

of G(V

, V

; C

) shown in

Fig. 3(d), nodes i and a are two free nodes. The

alternating graph with respect to M

is shown in Fig.

7(a). It is redrawn in Fig. 7(b) for a clear

explanation.

In order to resolve the non-transit virtual nodes

in V

’, we will combine

and

by connecting

(a) (b)

f’

’

b’

f’

(a)

(d)

(b)

(c)

(e)

f’

’:

(f)

f’

(g)

’

’:

(h)

’

(a)

(b) (c)

’:

i’

a’

i’

a’

c i

b i’

h a’

ICEIS 2009 - International Conference on Enterprise Information Systems

some nodes v’ in

to some nodes u in

if the

following conditions are satisfied.

(i) v’ is a non-transit virtual node appearing in V

’.

(Note that V(

) = V

i+1

∪ V

’.)

(ii) There exist a node x in V

i+1

and a node y in V

such that (x, v’) ∈ M

i+1

, x → y ∈ C

i+1

, and (y, u)

∈ M

We denote this combined graph by

⊕

Figure 7: An alternating graph.

For illustration, consider G(V

, V

’; C

) shown in

Fig. 4(a). Assume that the found maximum matching

is as shown in Fig. 4(b). Then, the alternating

graph

(with respect to M

) is a graph shown in

Fig. 8(a).

⊕

is shown in Fig. 8(b). Note that

i’ and a’ are two non-transit virtual nodes.

Figure 8: Illustration for combined graph.

We also remark that a node in

and a node in

may share the same node name. But they will be

handled as different nodes. For example, node e in

and node e in

are different.

In Fig. 8(b), we connect node a’ (in

) to node f

(in

) for the following reason.

(1) a’ is a non-transit virtual node introduced into

(2) (g, a’) ∈ M

, g → e ∈ C

, and (e, f) ∈ M

As mentioned above, we connect a’ to f since it

is possible for us to transfer the edges on an

alternating path (relative to M

) starting from node f

(relative to M

) and terminating at free node i or a

(in V

), which will make i or a covered without in-

creasing the number of chains.

The same analysis applies to node i’ (in

which is also connected to node f (in

In order to resolve as many non-transit virtual nodes

(appearing in V

’) as possible, we need to find a

maximum set of node-disjoint paths (i.e., no two of

these paths share any nodes), each starting at a non-

transit virtual node (in

) and ending at a free

node in

, or ending at a free node in

. For

example, to resolve a’ and i’, we need first to find

two paths in the above combined graph, as shown in

Fig. 9(a).

Figure 9: Illustration for node-disjoint paths.

(In Fig. 9(b), we show another two node-disjoint

paths.)

By transferring the edges on such a path, the

corresponding virtual node can be removed as

follows.

(1) Let v

→ v

→ ... → v

be a found path. Transfer

the edges on the path.

(2) If v

is a node in

, we simply remove the

corresponding virtual node v

(3) If v

is a node in

, connect the parent of v

along the corresponding chain to v

. Remove v

For instance, by transferring the edges on the path

from a’ to e (in

) in Fig. 9(a), we will connect g

to e (in

). a’ will be removed. By transferring the

edges on the path from i’ to a in Fig. 9(a), we will

connect h (in

) to a, b to j, e to c, and d to f. Then,

i’ is removed. Note that a is in

and d is the parent

of i’ along a chain (see Fig. 4(c)). In this way, we

will change the chains shown in Fig. 4(c) to the

chains shown in Fig. 10(a) with all the virtual nodes

being removed. The number of chains is still 5.

By resolving node f’ in the chain set shown in Fig.

6(b), we will get a set of disjoint chains shown in

Fig. 10(b).

Figure 10: Minimum sets of chains.

(a)

c i

d b

(b)

(a)

(b)

e c b

h a

a’

e c b

a’

i’

(a)

e c b

(b)

DIRECTED ACYCLIC GRAPHS AND DISJOINT CHAINS

It remains to show how to find a maximal set of

node-disjoint paths in

⊕

For this purpose, we define a maximum flow

problem over

⊕

(with multiple sources and

sinks) as follows.

1) Each non-transit virtual node in

designated as a source. Each free node (in

)

relative to M

i+1

, or free node (in

) relative to M

is designated as a sink.

2) Each edge u → v is associated with a capacity

c(u, v) = 1. (If (u, v) is not an edge in

⊕

c(u, v) = 0.)

Generally, to find a maximum flow in a network,

we need O(n

) time (Even, 1979; Karzanov, 1974;

Cotman et al., 2001). However, a network as

constructed above is a 0-1 network. In addition, for

each node v, we have either d

(v) ≤ 1 or d

out

(v) ≤ 1,

where d

(v) and d

out

(v) represent the indegree and

outdegree of v in

⊕

, respectively. It is

because each path in

⊕

is an alternating path

relative to M

i+1

or relative to M

. So each node

excerpt sources and sinks is an end node of an edge

covered by M

i+1

or by M

. As shown in (Even, 1979,

Theorem 6.3 on page 120), it needs only O(

time to find a maximum flow in this kind of

networks. Especially, a maximum flow exactly

corresponds to a maximal set of disjoint paths. See

the proof of Lemma 6.4 in (Even, 1979, page 120.)

According to the above discussion, we give the

following algorithm for resolving virtual nodes. We

assume that each virtual node has a parent along a

chain. Otherwise, it can be simply eliminated.

Algorithm virtual-resolution(S)

input: S - a chain set obtained by executing the chain

generation process.

output: a set of chains containing no virtual nodes.

begin

1. for i = h - 2 downto 1 do

2. {for any transit virtual node v’ in V

’ do

3. {

4. let u, v’, w be three consecutive nodes on a

chain;

5. connect u and w;

6. }

7. construct

⊕

; (*Begin to handle

non-transit virtual nodes.*)

8. find a maximal

set of node disjoint paths: P

, ... P

;

9. for j = 1 to l do

10. {let P

= v

→ v

→ ... → v

;

11. if v

is a free node relative to M

then

12. {transfer the edges on P

; remove v

;}

13. else (* v

is a free node relative to M

i-1

.*)

14. {let u be a node such that (u, v

) ∈ M

;

15. transfer the edges on P

; remove v

;

16. connect u to v

;

17. }

18. removed any unsolved virtual node;

19. }

end

In the main for-loop of the above algorithm, we

first handle transit virtual nodes (lines 2 - 6). Then,

we construct

⊕

1−

to resolve all the non-transit

virtual nodes (see line 7.) For this purpose, we

search for a maximal set of node disjoint paths (see

line 8). We also distinguish between two kinds of

node disjoint paths: paths ending at a free node

relative to M

, and paths ending at a free node

relative to M

i-1

. For the first kind of paths, we simply

transfer the edges on a path and then remove the

corresponding virtual node (see line 12). For the

second kind of paths, we need to do something more

to connect the parent of the corresponding virtual

node (along the chain) to the second node of the path

(see line 16). In line 18, we remove all those virtual

nodes, which cannot be resolved. Each of such

virtual nodes leads to splitting of a chain into two

chains.

Note that removing a transit virtual node will not

increase the number of chains. Also, resolving a

non-transit virtual node using a node disjoint path

does not lead to a chain splitting. So the number of

increased chains during the virtual node resolution

process is minimum since the number of node

disjoint paths is maximum.

3 TIME COMPLEXITY

Now we analyze the computational complexities of

our algorithm. The cost of the whole process can be

divided into three parts:

- cost

: the time for stratifying a DAG.

- cost

: the time for generating disjoint chains,

which may contain virtual nodes.

- cost

: the time for resolving virtual nodes.

As shown in (Chen and Chen, 2008), cost

bounded by O(n + e).

cost

mainly contains two parts. One part: cost

is the time for finding a maximum matching of every

G(V

, V

i-1

’; C

) (i = 1, ..., h - 1; V

’ = V

). The other

part: cost

is the time for checking whether, for each

actual free node appearing in V

i-1

’, there exists an

ICEIS 2009 - International Conference on Enterprise Information Systems

edge (v

, v

) covered by M

such that v

and v are

connected through an alternating path relative to M

The time for finding a maximum matching of G(V

i-1

’; C

) is bounded by

1−

· | C

’|). (see Chen et al., 2008)

Therefore, cost

is bounded by

∑

−

⋅+

|'|||

’|)

≤ O(

∑

−

⋅

Vbb

) = O(b

n).

cost

can be analyzed as follows. We construct a

small boolean n

× m

matrix A

, where n

is the

number of free actual nodes in V

i-1

and m

is the

number of all the covered actual nodes in V

. Each

entry a

= 1 in A

indicates that there exists an

alternating path (relative to M

) connects node j and

k. Using the algorithm discussed in (Coppersmith et

al., 1990) for matrix multiplication, cost

can be

estimated by

Ο(

∑

−

376.2

|)||(|

)

= Ο(

376.0

|)||)(|||||||2|(|

iiii

VVVVVV +++

−

−−

∑

)

≤ O(

∑

−

⋅

Vbb

) = O(b

n).

During the virtual-resolution process, the virtual

nodes are resolved level by level. At each level, the

number of the nodes in

⊕

1−

is bounded by

O(|V

i+1

| + 2|V

’| + |V

i-1

’|); and the number of its edge

is O(|C

| + |C

i-1

|). So, the time for finding a maximal

set of node-disjoint paths in

⊕

1−

is bounded

by O(

|'||'|2|

11 −+

iii

VVV

(|C

| + |C

i-1

|)). So the

total cost of the virtual node resolution is in the

order of

∑

−

−+

|'||'|2|'|

iii

VVV

· (|C

| + |C

i-1

|).

= O(

∑

−

⋅

Vbb

) = O(b

n).

From the above analysis, we get the following

proposition.

Proposition 1. The time complexity of the whole

process to decompose a DAG into a minimized set

of disjoint chains is bounded by O(bn

The space complexity of the whole process is

bounded by O(e + bn) since the number of the newly

added edges in each bipartite graph G(V

, V

i-1

’; C

’)

is bounded by O(b|V

i-1

|), and the size of each matrix

is bounded by O(|V

i-1

4 CONCLUSIONS

In this paper, a new algorithm for resolving virtual

nodes is discussed, which is a critic step in an

algorithm proposed by Chen

et al. (Chen and Chen,

2008) to decompose a DAG into a set of disjoint

chains. In addition, the virtual node resolution

process of Chen’s algorithm is analyzed, showing

that in some cases Chen’s algorithm fails to find a

minimal set of disjoint chains. The main idea of our

algorithm is the construction of alternating graphs.

By finding a maximal set of node disjoint paths in

such a graph to resolve virtual nodes, we are able to

guarantee that at each step of virtual node resolution,

the number of increased chains is minimum.

REFERENCES

H. Alt, N. Blum, K. Mehlhorn, and M. Paul, Computing a

maximum cardinality matching in a bipartite graph in

time O(n

1.5

), Information Processing Letters,

37(1991), 237 -240.

A. S. Asratian, T. Denley, and R. Haggkvist, Bipartite

Graphs and their Applications, Cambridge University,

1998.

J. Banerjee, W. Kim, S. Kim and J.F. Garza, "Clustering a

DAG for CAD Databases," IEEE Trans. on Knowl-

edge and Data Engineering, Vol. 14, No. 11, Nov.

1988, pp. 1684-1699.

K. S. Booth and G.S. Leuker, “Testing for the consecutive

ones property, interval graphs, and graph planarity

using PQ-tree algorithms,” J. Comput. Sys. Sci.,

13(3):335-379, Dec. 1976.

Y. Chen and Y. Chen, An Efficient Algorithm for An-

swering Graph Reachability Queries, Proceedings of

ICDE, 2008, pp. 893 - 902.

Y. Chen, “On the Graph Traversal and Linear Binary-

chain Programs,” IEEE Transactions on Knowledge

and Data Engineering, Vol. 15, No. 3, May 2003, pp.

573-596.

N. H. Cohen, “Type-extension tests can be performed in

constant time,” ACM Transactions on Programming

Languages and Systems, 13:626-629, 1991.

E. Cohen, E. Halperin, H. Kaplan, and U. Zwick,

Reachability and distance queries via 2-hop labels,

SIAM J. Comput, vol. 32, No. 5, pp. 1338-1355, 2003.

J. Cheng, J.X. Yu, X. Lin, H. Wang, and P.S. Yu, Fast

computation of reachability labeling for large graphs,

in Proc. EDBT, Munich, Germany, May 26-31, 2006.

D. Coppersmith, and S. Winograd. Matrix multiplication

via arithmetic progression. Journal of Symbolic

Computation, vol. 9, pp. 251-280, 1990.

DIRECTED ACYCLIC GRAPHS AND DISJOINT CHAINS

R. P. Dilworth, A decomposition theorem for partially

ordered sets, Ann. Math. 51 (1950), pp. 161-166.

S. Even, Graph Algorithms, Computer Science Press, Inc.,

Rockville, Maryland, 1979.

J. E. Hopcroft, and R.M. Karp, An n2.5 algorithm for

maximum matching in bipartite graphs, SIAM J. Com-

put. 2(1973), 225-231.

H. V. Jagadish, "A Compression Technique to Materialize

Transitive Closure," ACM Trans. Database Systems,

Vol. 15, No. 4, 1990, pp. 558 - 598.

A. V. Karzanov, Determining the Maximal Flow in a

Network by the Method of Preflow, Soviet Math.

Dokl., Vol. 15, 1974, pp. 434-437.

T. Keller, G. Graefe and D. Maier, "Efficient Assembly of

Complex Objects," Proc. ACM SIGMOD Conf., Den-

ver, Colo., 1991, pp. 148-157.

H. A. Kuno and E.A. Rundensteiner, "Incremental

Maintenance of Materialized Object-Oriented Views

in MultiView: Strategies and Performance

Evaluation," IEEE Transactions on Knowledge and

Data Engineering, vol. 10. No. 5, 1998, pp. 768-792.

T. Cotman, C. Leiserson, R. Rivest, and C. Stein, Intro-

duction to Algorithms (second edition), McGraw-Hill

Book Company, Boston, 2001.

R. Schenkel, A. Theobald, and G. Weikum, Efficient

creation and incrementation maintenance of HOPI in-

dex for complex xml document collection, in Proc.

ICDE, 2006.

R. Tarjan: Depth-first Search and Linear Graph Algo-

rithms, SIAM J. Compt. Vol. 1. No. 2. June 1972, pp.

146 -140.

J. Teuhola, "Path Signatures: A Way to Speed up Recur-

sion in Relational Databases," IEEE Trans. on Knowl-

edge and Data Engineering, Vol. 8, No. 3, June 1996,

pp. 446 - 454.

H. S. Warren, “A Modification of Warshall’s Algorithm

for the Transitive Closure of Binary Relations,” Com-

mun. ACM 18, 4 (April 1975), 218 - 220.

H. Wang, H. He, J. Yang, P.S. Yu, and J. X. Yu, Dual La-

beling: Answering Graph Reachability Queries in

Constant time, in Proc. of Int. Conf. on Data

Engineering, Atlanta, USA, April -8 2006.

S. Warshall, “A Theorem on Boolean Matrices,” JACM, 9.

1(Jan. 1962), 11 - 12.

Y. Zibin and J. Gil, "Efficient Subtyping Tests with PQ-

Encoding," Proc. of the 2001 ACM SIGPLAN Conf. on

Object-Oriented Programming Systems, Languages

and Application, Florida, October 14-18, 2001, pp. 96-

107.

ICEIS 2009 - International Conference on Enterprise Information Systems