
ONTOLOGY MAPPING BASED ON ASSOCIATION RULE
MINING
C. Tatsiopoulos and B. Boutsinas
University of Patras, Artificial Intelligence Research Center, GR-26500, RIO, Greece
University of Patras, Department of Business Administration, GR-26500, RIO, Greece
Keywords: Ontology Mapping, Interoperability, Association Rule Mining.
Abstract: Ontology mapping is one of the most important processes in ontology engineering. It is imposed by the
decentralized nature of both the WWW and the Semantic Web, where heterogeneous and incompatible
ontologies can be developed by different communities. Ontology mapping can be used to establish efficient
information sharing by determining correspondences among such ontologies. The ontology mapping
techniques presented in the literature are based on syntactic and/or semantic heuristics. In almost all of
them, user intervention is required. In this paper, we present a new ontology mapping technique which,
given two input ontologies, is able to map concepts in one ontology onto those in the other, without any user
intervention. It is based on association rule mining applied to the concept hierarchies of the input ontologies.
We also present experimental results that demonstrate the accuracy of the proposed technique.
1 INTRODUCTION
Ontology engineering, i.e. designing, developing,
maintaining and sharing ontologies, is an emerging
knowledge engineering process. It allows the
information organization into taxonomies of
concepts, represented by attributes, and relationships
between concepts, represented by IS-A relations,
functions, constraints, etc. Ontologies find
acceptance in numerous applications, e.g.
information retrieval (Pretschner & Gauch, 1999),
document management (Lacher & Groh, 2001),
agent communication (Huhns & Singh, 1997),
finance (Firat, & Madnick, 2001) and e-commerce
(Omelayenko, 2001). However, ontologies are
imposed by the explosive growth of the Semantic
Web, where they are used to describe the semantics
of the data. They are used for conceptually
structuring data and for knowledge sharing.
Ontologies can be designed and developed by
different groups of people with similar interests, i.e.
communities within the so-called information
society, either through knowledge engineering
processes or through automated knowledge
extraction methods.
One of the most important properties of both the
WWW and the Semantic Web is decentralization
((Berners-Lee, 1999), W3C
). Therefore, ontologies
can be designed and developed by different
communities without adopting common standards
for information exchange. On the other hand, the
leverage of synergies of information exchange has
been increased by the deployment of systems for
community interaction support. Many researchers
(e.g. (Lacher & Groh, 2001), (Maedche & Staab,
2000), (Mitra & Wiederhold, 2002), (Stumme &
Maedche, 2001)) argue that common to all systems
ontologies can not be guarantied (see (Wache,
Vögele, Visser, Stuckenschmidt, Schuster, Neumann
& Hübner, 2001) for a survey of such effort),
because it is more efficient if a smaller community is
involved in the process and, in general, communities
can usually not be forced to adopt common
standards. Then an efficient ontology-based
information exchange can be established by solving
the problem of determining correspondences among
different ontologies, i.e. determining the set of
similar, overlapping or unique concepts. This
problem is an instance of the interoperability
problem (e.g. (Park & Ram, 2004)) which concerns
the connection of information systems that are
heterogeneous and incompatible. Recently, this
problem has been a major focus of both the research
and the practitioner communities. Both data and
knowledge engineering has been focused on
identifying correspondences between ontologies and
33
Tatsiopoulos C. and Boutsinas B. (2009).
ONTOLOGY MAPPING BASED ON ASSOCIATION RULE MINING.
In Proceedings of the 11th International Conference on Enterprise Information Systems - Information Systems Analysis and Specification, pages 33-40
DOI: 10.5220/0001862800330040
Copyright
c
SciTePress

between database schemas respectively (e.g. (Choi,
Song & Han, 2006), (Kalfoglou & Schorlemmer,
2003), (Rahm & Bernstein, 2001), (Shvaiko &
Euzenat, 2005)). Ontology heterogeneity and
incompatibility is due to the existence of knowledge
either in different structures or in different
environments with different semantics. Ontology
mapping aims at tackling structural and semantic
heterogeneity and incompatibility by determining
correspondences between elements of disparate
ontologies. Note that structural heterogeneity has
also been addressed to a great extent in the schema
matching literature (Rahm & Bernstein, 2001). A
mapping can be established either directly between
two ontologies (alignment) or indirectly through
mapping them onto a third reference ontology which
both of them share as a common upper model
(articulation). The work of mapping ontologies is
performed mostly by hand, perhaps supported by a
graphical user interface. Of course, performing
ontology mapping manually is an extremely time-
consuming and error-prone process. The ontology
mapping techniques presented in the literature are
usually based on syntactic and/or semantic
heuristics. The latter have been studied in various
scientific fields including machine learning, concept
lattices, formal theories, databases and linguistics. In
almost all of them user intervention is required, thus
they are semi-automated. Usually, when an
automatic decision is not possible, these techniques
suggest possible correspondences, determine
conflicts and propose solutions and actions. Then the
user makes the final selection. In this paper, we
present a new ontology mapping technique, which,
given two input ontologies, is able to map concepts
in one ontology onto those in the other, without any
user feedback. The proposed technique exploits the
structure of the input ontologies, i.e. the concept
hierarchies, to determine the mapping. More
specifically, in the proposed ONARM technique,
ONtology mapping is based on Association Rule
Mining, which extracts association rules from these
concept hierarchies. Association is one of the most
popular data mining tasks. Association rules can be
used to represent frequent patterns in data, in the
form of dependencies among concepts-attributes.
The extracted association rules are considered as
indirectly describing the concept relationships. Note
that, despite the support or the controversy of the
statement that ontology mapping is similar to
database schema matching ((Kalfoglou &
Schorlemmer, 2003), (Noy & Klein, 2002)), the
proposed methodology can be applied to both of
them. In the rest of the paper we first present related
work (Section 2) and then we present the proposed
ontology mapping technique (Section 3). Next, we
present experimental results of testing its accuracy
and efficiency (Section 4). We also discuss its time
complexity (Section 5) and finally we conclude
(Section 6).
2 PREVIOUS APPROACHES
Recently, the number of ontology matching
techniques and systems has increased significantly
(OMO, Ontology Matching Organisation for a
complete information on the topic). Ontology
mapping techniques vary in input and output formats
as well as in modes of user intervention. There has
been little work on the comparative evaluation of
ontology mapping techniques in the literature (e.g.
(Giunchiglia, Yatskevich, Avesani & Shvaiko,
2008), (Kalfoglou & Schorlemmer, 2003), (Kaza &
Chen, 2008)).
There are techniques which simply guide the
user to create the mappings, e.g. PROMPT (Noy &
Musen, 2000), SMART (Noy & Musen, 1999),
PROMPTDIFF (Noy & Musen, 2002), CHIMAERA
(
McGuinness, Fikes , Rice & Wilder, 2000).
There are also semi-automatic techniques in
which the user has to resolve conflicts and
duplicates, FCA-Merge (Stumme & Maedche,
2001), to create mappings for concepts that cannot
be matched, GLUE (Doan, Madhavan , Domingos
&, Halevy, 2002), to validate the matches, ONION
(Mitra & Wiederhold, 2002). Also, some techniques
allow user to suggest matches apart from those
created automatically, e.g. EER-CONCEPTOOL
(Compatangelo & Meisel, 2003).
Moreover, there are techniques which create the
mapping automatically, e.g. CAIMAN (Lacher &
Groh, 2001), IF-Map (Kalfoglou & Schorlemmer,
2002), ITTalks (Prasad, Peng & Finin, 2002),
MAFRA (Maedche, Motik, Silva & Volz, 2002), S-
MATCH (Giunchiglia, Shvaiko & Yatskevich,
2004).
Additionally, there are techniques which are
based on the combination of different matching
processes (e.g. (Aumueller, Do, Massmann & Rahm,
2005), (Hu & Qu, 2008)), which exhibit remarkable
results in term of accuracy (OAEI).
There are also techniques that could potentially
be used in ontology mapping like translators (e.g.
OntoMorph (Chalupksy, 2000)) or integrators (e.g.
Hovy, 1998). Finally, a similar problem is that of
schema matching in databases. However, most
schema matching techniques are not adequate for
ICEIS 2009 - International Conference on Enterprise Information Systems
34

ontology mapping due to not handling differences in
terminology, due to exhibiting poor results in the
case of little structural similarity, due to absence of
instances, etc.
3 THE PROPOSED TECHNIQUE
The key idea of the proposed technique is to
establish a similarity between two concepts of the
input ontologies, which is based on their location in
the ontology structures. The location of a node, that
represents a concept within an ontology structure,
determines its neighbour concepts. We consider that
the meaning of a concept is also characterized by the
meaning of its neighbour concepts, as the creator of
the ontology indirectly determined by defining the
structure of the ontology.
Note that structural mapping alone is not
sufficient for ontology mapping. The meaning of the
concept is also characterized by a linguistic analysis
of the concept with respect to a large-scale
dictionary like WordNet, to a corpus of documents,
to manual rules, to lexical distances, etc. The
proposed technique accepts both of these sources of
background knowledge in order to establish a
similarity measure. However, the latter is dominated
by the location of a concept within the ontology.
Graph matching techniques could be used in
order to examine the similarity of the location of two
input concepts. Since we concentrate on efficiency,
we rejected such techniques because of their time
complexity (for instance time complexity of graph
isomorphism is exponential). The proposed
technique considers each path of the ontology
structure as a source of background knowledge. It
applies association rule mining in order to determine
the predominant neighbour concepts of an input
concept.
In this paper, we consider association rule
mining that is known as the market basket problem,
where concepts-attributes represent products and the
initial database is a set of customer purchases
(transactions). This particular problem is well-
studied in data mining. We consider association
rules analog to the form “90% of the customers that
purchase product x also purchase product y”
(Boolean association rules) (e.g. (Agrawal, Mannila,
Srikant & Verkamo, 1996), (Brin, Motwani, Ullman
& Tsur, 1997), (Park, Chen & Yu, 1995)).
Formally, an association rule is a rule of the form
X Y, where X,Y named respectively antecedent
and consequent of the rule and X,Y I = {i
1
,i
2
,
…i
j
}, such that XI Y =
⇒
⊂
∅
and i
k
, 1 k j is an
item in the transaction database D. The informative
power (named interestingness) of each association
rule is measured by two indexes: the “support” that
measures the proportion of transactions in D
containing both X and Y and the “confidence” that
measures the conditional probability of the
consequent given the antecedent.
≤ ≤
More specifically, the proposed technique
considers each path of the ontology structure as a
transaction. Then, for each input ontology, it applies
association rule mining to the set of its transactions.
We consider that the extracted association rules
determine the predominant neighbour concepts of
every input concept. Thus, the similarity of these
association rules defines the location-based
similarity of the concepts.
Linguistic analysis is also taken into
consideration. However, it is used to increase or
decrease the obtained location-based similarity (see
γ parameter below). In that sense, any heuristic for
linguistic analysis proposed in the literature can be
used. Also, aggregating the results of such heuristics
could also be used, as for example presented in
(Ehrig & Staab, 2004), (Ehrig & Sure, 2004). In this
paper, we adopt a naive such heuristic: we examine
identity of labels of concepts, while we use a
common vocabulary for both ontologies. Obviously,
more advanced heuristics would increase the overall
accuracy.
The proposed technique can be applied to
ontology structures forming a directed acyclic graph.
Thus, it supports multiple inheritance. The required
formal definition of input ontologies contains two
core items shared by most formal definitions of an
ontology in the literature: concepts and a
hierarchical IS-A relation. Thus, we define a core
ontology as: a pair G = (C, r), where C is a set of
concepts and r is a partial order on C, i.e. a binary
relation r
∈
C x C which is reflexive, transitive, and
antisymmetric.
More specifically, the proposed technique
accepts two ontologies as input. Any ontology editor
can be used to create them (we used the Protégé
knowledge-modeling environment). During a first
step the input ontologies are transformed to RDF
and RDFS formats. Obviously, any ontologies pre
described in RDF(s) can be used. Then, the Java –
Jena API is used. Jena is a Java implementation of
an extension to the semantic web by means of a
respective API. This offers the capability of getting
the complete description of the input ontology in
terms of its structural elements (paths, current nodes,
successor nodes, parent nodes, siblings and leaf
ONTOLOGY MAPPING BASED ON ASSOCIATION RULE MINING
35

nodes). In order to apply the APRIORI association
rule mining algorithm (Agrawal et al.), nodes must
be topologically numbered. Thus, the second step is
to generate a numbered node structure, of the same
structure as the ontology under examination but
numbered with integer numbers that will undergo
Breadth First Search (BFS), such that, integers are
horizontally incremented and assigned and therefore
guaranteeing this way, that any node N
i
is numbered
with an integer k such that k>m, where m is the
integer which has been assigned to its parent node M
(this relation holds true for any parent and child
nodes within the input ontology). This way, nodes
at deeper levels are mapped with higher number
values.
After numbering the Ontology, the result is a
hash table that includes all the nodes of the ontology
with their respective integers. Then, to extract all
the possible paths, with the objective to quick reach
and examine with priority terminal nodes its paths, a
Depth First Search (DFS) is run, that provides all
possible paths number-named in a list type format.
The methodology has been designed in such a way
that permits multiple inheritance (and therefore has
multiple parents) in the following way and under the
definition:
L(i) is the level of this node i and
Li = max(l1, l2,..ln), where,
l1, l2,…, ln are level numbers to which the node
i belongs simultaneously.
To resolve the above, during the numbering
process, the integers that are assigned to nodes are
non-continuous but retain the necessary property
needed for the APRIORI algorithm that follows,
such that:
for any two nodes I,J, order (J) > order (I), where
node J is parent of node I.
This step involves the extraction of all root-to-
leaf paths available in the ontology schema, by
means of a recursive method. Furthermore, a list of
all leaf nodes is created.
Then, for a predefined set of minimum support
and confidence values, APRIORI algorithm is
applied to both input ontologies (e.g. G
1
and G
2
).
The result is a set of rules of the following type:
1: { [2, 7], 45, 20}
3: { [1, 7, 4], 30, 70}
4: { [1, 3, 6], 45, 20}
5: { [1, 3, 4], 30, 70}
………
where, the integers above denote number-named
nodes of the ontology. Each pair of (c,s) produces
such one respective set of rules R(G
1
), R(G
2
).
Following, the above rule set is back translated and
represented with the original node names, providing
this way R’(G
1
), R’(G
2
) of rules.
The ONARM technique generates an [n x m]
“significance matrix” containing the significance in
matching every node of G
1
=(C
1
, r
1
) with every one
of G
2
=(C
2
, r
2
). Note that G
2
is mapped against G
1
and not vice versa, considering G
1
as our reference
ontology. The significance in matching XЄC
1
to
YЄC
2
is calculated based on the support measure of
the association rules having X and Y as left part. For
instance, consider the following rules for X and Y:
X→(B,s1), X→(BC,s2), Y→(B,s3), Y→(AC,s4)
For each of the four pairs of rules, one for X and the
other for Y, the measures K and Kt, indicating the
significance, are computed by the following
procedure:
1. K=0, if |s
X
– s
Y
| > α, where α a user defined
threshold
2. K ← Average(s
X ,
s
Y
) * β * w, where
β > 1 if X or Y or both are instances,
β = 1 otherwise,
w = percentage of similarity of right parts
3. Kt = K * γ, where
γ > 1 if X ≡ Y, i.e. the two nodes are
identical after a linguistic analysis
γ = 1 otherwise.
Thus, processing the pair (X→(B,s1),Y→(B,s3))
K=Average(s1,s3)*1*1, processing the pair (X→
(B,s1),Y→(AC,s4)) K=Average(s1,s4)*1*0 and
processing the pair (X→ (BC,s1),Y→(AC,s4))
K=Average(s1,s4)*1*0.5
Then, the matrix is filled as follows:
For every cell (i ,j ) in the [n x m] matrix
a. Calculate
∑
p
K, for every pair p of
rules, one for i and the other for j
b. Calculate Kt
c. Fill cell (i, j) with Kt
d. Reduce considered cases by using
constraint of maximal selection of Kt,
for subsequent analyses.
Continue
until all ( i,j) cases are filled and reduced.
ONARM, for some minimum support and
confidence (e.g. (s,c)=(25,5)) extracts rules from two
ontologies (e.g. G
2,
G
3
) and builts the significance
matrix (e.g. see Table 1). Finally, it provides final
mappings along with their significance, e.g.:
[G2]:ooo50 -> [G3]:ooo50 75.0
In the example of Table 1, nodes of G
2
are listed
in rows and those of G
3
are listed in columns of
significance matrix, while cells contain the
significance.
ICEIS 2009 - International Conference on Enterprise Information Systems
36
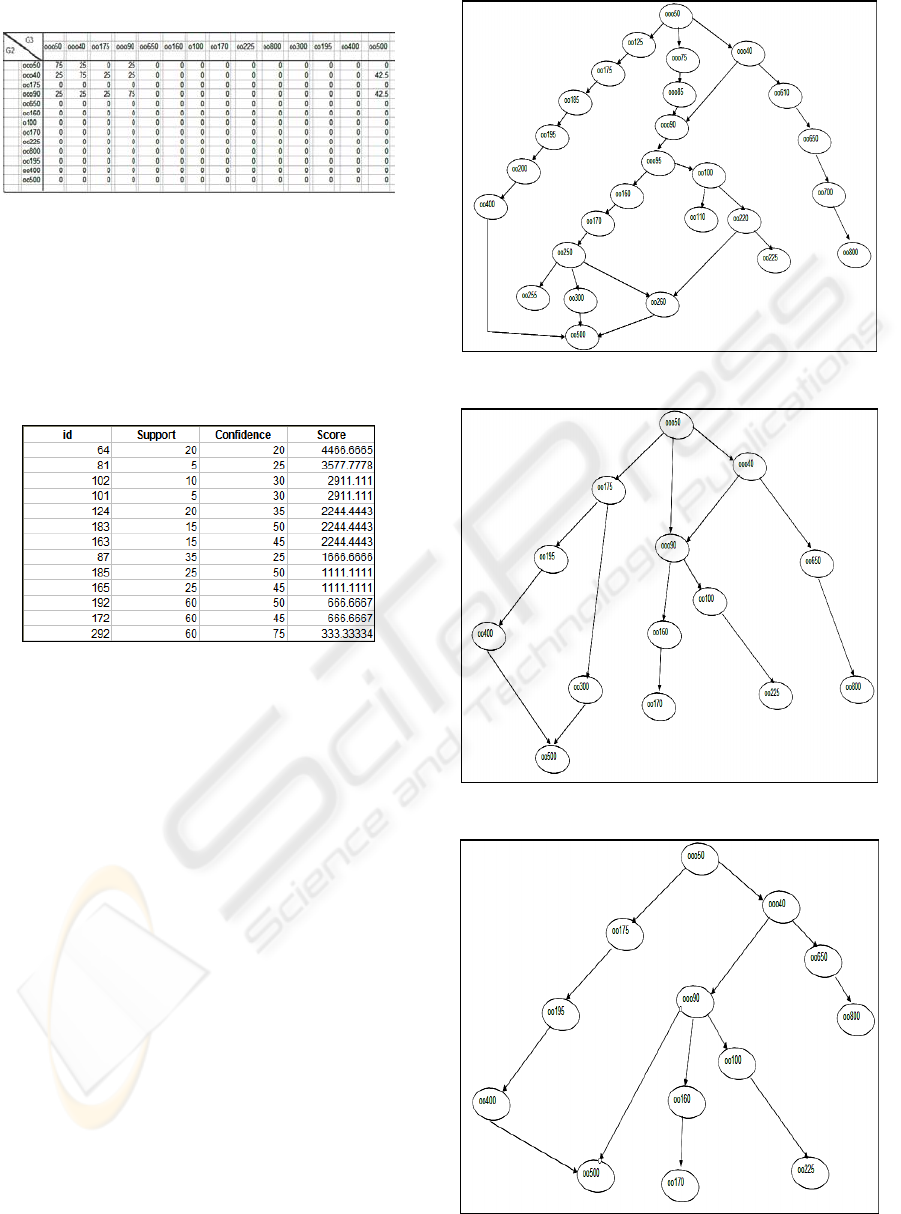
Table 1: A portion of the significance matrix.
4 EMPIRICAL RESULTS
For evaluation purposes, a total of 400 combinations
of (s,c) are examined. All 400 cases of possible (s,c)
are summarized in Table 2:
Table 2: Accuracy w.r.t. support and confidence.
What is depicted in the above cumulative
summarized table (only some entries are presented
out of the 400 possible), is the relevance of the final
score used for the mapping, in terms of support and
confidence parameters, that have been run against
and are presented in descending manner, from the
most relevant to the least.
Empirical tests aim at examining the accuracy of
the proposed technique and for this reason the
following experiment has been set up.
Consider three Ontologies G
1
, G
2
and G
3
, in such
a way that G
2
is directly derived from G
1
and G
3
directly derived from G
2
(see Figures 1-3).
Therefore G
1
is considered as the Reference
Ontology that we run tests against for G
2
, G
3
.
After applying ONARM to them in a manner of
G
2
against G
1
and G
3
against G
1
we obtain the
following summarized results:
a) For the comparison and mapping of the G
1
and
G
2
Ontologies, ONARM found 76 correct
matchings between them. The best cases were
found in the areas where the minimum support
was between 5% - 40% and the minimum
confidence 5% - 65%. Thus, minimum support
and c onfidence values are not critical. The only
Figure 1: Test ontology G
1.
Figure 2: Test ontology G
2.
Figure 3: Test ontology G
3.
ONTOLOGY MAPPING BASED ON ASSOCIATION RULE MINING
37

requirement is to set low values. Theoretically,
this is true because of the small number of paths
of an ontology.
b) In the last column is presented the number of
matches per case, as non-zero-values
[NonZeroVal].
c) The average, variance and standard deviation
analysis is based upon the score that has been
assigned to each case, as Kt, as described in the
theoretical background section.
d) Cumulative results are presenting, in a more
analytical way, in Table 3 (for G
1
) and Table 4 (
for G
2
) for an indicative set of values (s,c):
Table 3: Cumulative results for G
1
.
Table 4: Cumulative results for G
2
.
Given the above, for G
1
& G
3
the success rate is
149 cases out of 400 for the first mapping attempt,
i.e., 38%, while in the comparison of G
2
& G
3
the
success rate increases dramatically to 220 out of 400
cases, i.e., 55%,. Analytical results exist for all the
above cases too, providing similar distribution in
respect to support and confidence of the success
cases.
It is important to note here, that the percentages
refer to the average of all cases of s, c. To continue
our investigation, we consider the comparison and
mapping of G
2
& G
3
, for s = 5 and c = 5. In this
case, we obtain 11 full matches (FM), 2 zero
matches (ZM) and 0 partial matches (PM) as
follows:
FM(G
3
) = {ooo50, ooo40, oo175, ooo90, oo160,
oo100, oo170, oo225, oo 195, oo 400, oo500 }
PM(G
3
) = { }
ZM(G
3
) = {oo650, oo800}
The ZM(G
3
) is obtained since our methodology,
puts weight more in the structural elements of nodes,
than to their lectical name. Then, ONARM applies
linguistic analysis to nodes also of the final mapping
process, and adds ZM(G
3
) to FM(G
3
). This way,
concluding the process, the precision=1 and recall=1
for the specific mapping of nodes respectively. This
way, ONARM after its lectical mapping phase, finds
100% of correct mappings of G
2
and G
3
nodes. Note
that the case of G
1
& G
2
is similar.
5 DISCUSSING EFFICIENCY
Considering two input ontologies, the time
complexity of ontology mapping techniques
presented in the literature varies from the order of
O(|G
1
| * |G
2
|) (e.g. (Maedche et al.)) to exponential
(e.g. (Stumme & Maedche, 2001), (Giunchiglia, et
al., 2004)).
Recently, there is a concern on the efficiency of
the proposed in the literature ontology mapping
techniques. For instance the work presented in
(Ehrig & Staab, 2004) tries to reduce the search
space by introducing certain strategies to select the
pair of concepts checking for matching. Thus the
time complexity is reduced to
O( (|G
1
| + |G
2
|) * log(|G
1
| + |G
2
|))
In the proposed ONARM technique, the
extraction of association rules is performed
separately for each ontology, which is O(|G
i
|*|C
k
|),
where |C
k
|) is the number of all candidate itemsets
checked. According to (Agrawal et al.), the
complexity of locating the itemsets of size k is
O(klog(|G
i
| / k)) (however in random databases there
are only a few large itemsets). In ONARM the
maximum size is d, the depth of the ontology. Thus,
the latter complexity is O(∑
d
j=1
jlog(|G
i
|/j) which is
O(d
2
log(|G
i
|). Thus, the overall complexity of
extraction is O(d
2
log(|G
i
|). The used similarity
matrix is obtained in O(|G
1
|*|G
2
|).
6 CONCLUSIONS
We presented an ontology mapping technique,
ONARM, which exploits a structural similarity
measure in order to automatically determine the
ICEIS 2009 - International Conference on Enterprise Information Systems
38

mapping between two input ontologies. Since
ONARM is based on the structure of ontologies, it
can handle both metadata and instance
heterogeneity. ONARM can easily be included in
systems based on combination of matching
techniques, especially because only a few techniques
exist for only structural similarity ((Ehrig & Staab,
2004), (Euzenat & Valtchev, 2004), (
Hu, Jian, Qu &
Wang,
2005)). Note that ONARM exhibits a low
time complexity with respect to related approaches.
The meaning of the concepts is also taken into
consideration, (step 3 of the procedure calculating K
and Kt), by applying any linguistic analysis. Thus, it
is important to note that input ontologies might have
different label domains for node naming, without
reducing the efficiency of the proposed
methodology.
We plan to continue the evaluation of ONARM
using benchmark ontologies ((
Giunchiglia et al., 2008),
OAEI). Note that early results on specific OAEI-
2008 benchmarks (e.g. 101,102, 201-205, 223) show
almost the highest accuracy.
Also, we are currently working on extending
ONARM in order to automatically update each one
of the input ontologies with respect to the other, by
using a new distance measure (Boutsinas &
Papastergiou, 2008) of the similarity of two concepts
of the same ontology.
ACKNOWLEDGEMENTS
We are grateful to Kostas Sidiropoulos for his help
during the tests.
REFERENCES
Agrawal, R., Mannila, H., Srikant, R., Verkamo, A.I.,
1996. Fast Discovery of Association Rules, in:
(Fayyad, 1996), pp. 307-328.
Aumueller D., Do H.H., Massmann S., Rahm E., 2005.
Schema and ontology matching with COMA++,
Proceedings of SIGMOD (Demonstration).
Berners-Lee, T., 1999. Weaving the Web, Harper.
Boutsinas, B., Papastergiou, T., 2008. On clustering tree
structured data with categorical nature, Pattern
Recognition, 41(12), Elsevier Science, pp. 3613-3623.
Brin, S., Motwani, R., Ullman, J.D., Tsur, S., 1997.
Dynamic Itemset Counting and Implication Rules for
Market Basket Data, in: Proceedings of ACM
SIGMOD Int. Conf. Management of Data, pp. 255-
264.
Chalupksy, H., 2000. OntoMorph: a translation system for
symbolic knowledge, Proceedings of the 17th
International Conference on Knowledge
Representation and Reasoning (KR-2000).
Choi, N., Song, I.Y., Han, 2006. H., A Survey on
Ontology Mapping, SIGMOD Record 35(3), pp. 34-
41.
Compatangelo, E., Meisel, H., 2003. "Reasonable"
support to knowledge sharing through schema
analysis and articulation, Neural Computing &
Applications, - Springer.
Doan, A., Madhavan, J., Domingos, P, Halevy, A., 2002.
Learning to map between ontologies on the semantic
web, Proceedings of the 11th International World
Wide Web Conference (WWW 2002).
Ehrig, M., Staab, S., 2004. QOM— Quick Ontology
Mapping. In: Proceedings of the Third International
Semantic Web Conference, Springer.
Ehrig, M., Sure, Y., 2004. Ontology Mapping - An
Integrated Approach. In Proceedings of ESWS.
Euzenat J., Valtchev P., 2004. Similarity-based Ontology
Alignment in OWL-Lite, Proc. of ECAI, 2004, pp.
333-337.
Fayyad, U.M., Piatetsky-Shapiro, G., Smyth, P., 1996.
Advances in Knowledge Discovery and Data Mining,
AAAI Press/MIT Press.
Firat, A., Madnick, S., 2001. Knowledge Integration to
Ontological Heterogeneity: Challenges from
Financial Information Systems, in 23rd International
Conference on Information Systems (ICIS),
Barcelona, Spain.
Giunchiglia, F., Shvaiko, P., Yatskevich, M., 2004. S-
Match: an Algorithm and an Implementation of
Semantic Matching, In Proceedings of ESWS.
Giunchiglia, F., Yatskevich, M., Avesani, P., Shvaiko, P.,
2008. A Large Scale Dataset for the Evaluation of
Ontology Matching Systems, Knowledge Engineering
Review Journal, (to appear).
Hovy, E., 1998. Combining and Standardizing Large-
Scale, Practical Ontologies for Machine Translation
and Other Uses, proceedings of LREC.
Hu. W., Qu Y., 2008. Falcon-AO: A practical ontology
matching system, Web Semantics: Science, Services
and Agents on the World Wide Web, Volume 6, Issue
3, pp. 237-239.
Hu. W., Jian N., Qu Y., Wang Y., 2005. GMO: a graph
matching for ontologies, Proceedings of K-
CAPWorkshop on Integrating Ontologies, pp. 41-48.
Huhns, M.N., Singh, M.P., 1997. Ontologies for agents,
IEEE Internet Computing 1(6), pp. 81-83.
Kalfoglou, Y., Schorlemmer, M., 2002. Information-
flow-based ontology mapping, Lecture Notes in
Computer Science 2519, pp. 1132-1151.
Kalfoglou, Y. Schorlemmer, M., 2003. Ontology
Mapping: the State of the Art, The Knowledge
Engineering Review 18(1).
Kaza, S., Chen, H., 2008. Evaluating Ontology Mapping
Techniques: An Experiment in Public Safety
Information Sharing. Decision Support Systems
Volume 45, Issue 4, pp. 714-728, Information
Technology and Systems in the Internet-Era.
ONTOLOGY MAPPING BASED ON ASSOCIATION RULE MINING
39

Lacher, M.S., Groh, G., 2001. Facilitating the exchange
of explicit knowledge through ontology mappings,
Proceedings of the 14th International FLAIRS
Conference.
Maedche, A., Motik, B., Silva, N., Volz, R., 2002.
MAFRA — A MApping FRAmework for Distributed
Ontologies. In: Proceedings of the EKAW 2002.
Maedche, A., Staab, S., 2000. Semi-automatic
engineering of Ontologies from texts, Proceedings of
the 12th International Conference on Software
Engineering and Knowledge Engineering (SEKE
2000), pp. 231-239.
McGuinness D.L., Fikes R., Rice J., Wilder S., 2000. An
Environment for Merging and Testing Large
Ontologies, Proceedings of the Seventh International
Conference on Principles of Knowledge,
Representation and Reasoning (KR2000)
Breckenridge, Colorado.
Mitra, P., Wiederhold, G., 2002. Resolving
Terminological Heterogeneity In Ontologies,
Proceedings of the ECAI'02 workshop on Ontologies
and Semantic Interoperability.
Noy, N.F., Klein, M., 2002. Ontology evolution: not the
same as schema evolution, Also as: Smi-2002–0926,
University of Stanford, Stanford Medical Informatics.
Knowledge and Information Systems (In Press).
Noy, N.F., Musen, M., 1999. SMART: automated support
for ontology merging and alignment, Proceedings of
the 12th Workshop on Knowledge Acquisition,
Modelling and Management (KAW'99).
Noy, N.F., Musen, M., 2000. PROMPT: algorithm and
tool for automated ontology merging and alignment,
Proceedings of the 17th National Conference on
Artificial Intelligence (AAAI'00).
Noy, N.F., Musen, M., 2002. PROMPTDIFF: a fixed-
point algorithm for comparing ontology versions,
Proceedings of the 18th National Conference on
Artificial Intelligence (AAAI'02), pp. 744-751.
Omelayenko, B., 2001. Integration of product ontologies
for B2B marketplaces: a preview. SIGecom Exch.,
2(1).
Ontology Matching Organisation, (OMO)
http://www.ontologymatching.org
Park, J~S., Chen, M.~S., Yu, P.~S., 1995. An Effective
Hash-Based Algorithm for Mining Αssociation rules,
in Proceedings of ACM SIGMOD Int. Conf.
Management of Data, pp. 175-186.
Park, J., Ram, S., 2004. Information Systems
Interoperability: What Lies Beneath? ACM
Transactions on Information Systems 2004; 22(4),
pp. 595-632.
Prasad, S., Peng, Y., Finin, T.,2002. Using Explicit
Information To Map Between Two Ontologies .
Workshop on “Ontologies in Agent Systems”.
Pretschner, A., Gauch, S., 1999. Ontology based
personalized search, Proc. 11th IEEE Intl. Conf. on
Tools with Artificial Intelligence, pp. 391-398.
Rahm, E., Bernstein, P.A., 2001. A Survey of Approaches
to Automatic Schema Matching, VLDB Journal, 10(4).
Shvaiko, P., Euzenat, J., 2005. A Survey of Schema-based
Matching Approaches. Journal on Data Semantics
(JoDS), IV, LNCS 3730, pp. 146—171.
Stumme, G., Maedche, A., 2001. Ontology Merging for
Federated Ontologies on the Semantic Web,
Proceedings of the International Workshop for
Foundations of Models for Information Integration
(FMII- 2001).
Wache, H., Vögele, T., Visser, U., Stuckenschmidt, H.,
Schuster, Neumann, G., H., Hübner, S., 2001.
Ontology-Based Integration of Information - A Survey
of Existing Approaches, in IJCAI Workshop:
Ontologies and Information Sharing, Seattle, WA.
W3C, www.w3.org/DesignIssues/Principles.html.
ICEIS 2009 - International Conference on Enterprise Information Systems
40
