ALGORITHMS FOR EFFICIENT TOP-K SPATIAL
PREFERENCE QUERY EXECUTION IN A HETEROGENEOUS
DISTRIBUTED ENVIRONMENT
Marcin Gorawski and Kamil Dowlaszewicz
Institute of Computer Science, Silesian University of Technology, Akademicka 16, Gliwice, Poland
Keywords: Top-k Spatial Preference Query, Distributed, Heterogeneous, Adaptive, Scheduling, Algorithm.
Abstract: Top-k spatial preference queries allow searching for objects on the basis of their neighbourhoods’ character.
They find k objects whose neighbouring objects satisfy the query conditions to the greatest extent. The
execution of the queries is complex and lengthy as it requires performing numerous accesses to index
structures and data. Existing algorithms therefore employ various optimization techniques. The algorithms
assume, however, that all data sets required to execute the query are aggregated in one location. In reality
data is often distributed on remote nodes like for example data accumulated by different organizations. This
motivated developing algorithm capable of efficiently executing the queries in a heterogeneous distributed
environment. The paper describes the specifics of operating in such environment, presents the developed
algorithm, describes the mechanisms it employs and discusses the results of conducted experiments.
1 INTRODUCTION
A top-k spatial preference query specifies a target
data set and conditions describing the preferred
neighborhood of objects from that set (Yiu et al.,
2007). The conditions are based on non-spatial
attributes of objects from other data sets, which are
further called feature objects. The query also
specifies a method of finding the objects whose
attribute values will influence target objects’ score.
It can for example classify as such their nearest
neighbors or objects located within a specified
distance from the target objects.
An example of top-k spatial preference query is
a search for apartments having in their vicinity
restaurants offering a wide selection of vegetarian
food and convenient access to public transport.
Figure 1 illustrates the execution of such query.
White circles represent target objects which in this
case are residential buildings. Black circles represent
bus and train stations while gray circles represent
restaurants; depending on their chosen attribute
values target objects’ scores will be computed.
The conditions of the query illustrated on the
figure define neighboring objects as the ones least
distant from the target objects, which are pointed by
arrows. In this case object r1 is found to have the
highest value. Its total score amounts to 0.8+0.9=1.7,
while r2 object’s value equals 0.8+0.6=1.4, r4
object’s value equals 0.6+0.7=1.3 and r3 object’s
value equals 0.3+0.6=0.9.
X
Y
r
1
r
4
r
3
0,8
0,3
0,7
0,6
0,9
r
2
Figure 1: Schema of top-k spatial query execution.
Finding each partial score of an object requires
executing an appropriate spatial query which finds
objects located in the object’s neighborhood. The
queries can comprise many preferences and spatial
data sets are characterized by high cardinality. This
results in performing a large number of spatial
queries during each execution.
Therefore, the optimization technique introduced
in SP algorithm (Yiu et al., 2007) strives to discard
these objects whose maximum possible score is
lower than the score of k-th object classified as a
43
Gorawski M. and Dowlaszewicz K. (2009).
ALGORITHMS FOR EFFICIENT TOP-K SPATIAL PREFERENCE QUERY EXECUTION IN A HETEROGENEOUS DISTRIBUTED ENVIRONMENT.
In Proceedings of the 11th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages 43-48
DOI: 10.5220/0001863200430048
Copyright
c
 SciTePress

result at that moment. Another R-tree based
(Guttman, 1984) optimization method, introduced in
GP algorithm (Yiu et al., 2007), bases on
simultaneous computation of partial values of
objects stored in one index leaf. Finally, the
technique that simultaneously computes partial
values of an object, based on similar preferences can
be utilized (Gorawski and Dowlaszewicz, 2008.09).
Algorithms employing these techniques assume
that indices and data can be directly accessed and
that all information about the process is available
throughout their execution. Generally, in distributed
environments these conditions are not satisfied, thus
neccessitating developing adequate algorithm.
A similar problem has already been studied in
(Güntzer, Balke and Kießling, 2001), (Michel,
Triantafillou and Weikum, 2005) and (Bruno,
Gravano and Marian, 2002). The research concerns,
however, regular top-k queries and focuses e.g. on
efficient ranking creation when remote nodes hold
lists of partial scores. Executing top-k spatial
preference queries requires a specialized solution.
2 PROBLEM SPECIFICS
Determining the level of compliance of object’s
neighborhood with query conditions requires finding
objects basing on their location and reading the
values of their attributes. Therefore, when data sets
are located on remote nodes, it is necessary to send
all information required to execute the query through
the network. As data transmission is a relatively
lengthy operation, it is essential for algorithms
operating on distributed data to minimize the amount
of transmitted data. The specifics allow, however,
utilizing the resources of computers on which the
data is stored. Furthermore, in a distributed
environment the parameters of remote computers,
such as their load and network capacity, can vary.
Therefore, it is necessary to minimize the influence
of computers lacking available resources on the
query execution process. Finally it is essential to
utilize existing optimization techniques since they
proved to substantially reduce the number of index
and data accesses as presented in (Yiu et al., 2007)
and (Gorawski and Dowlaszewicz, 2008).
3 EXECUTION SCHEMA
The adopted solution bases on computing partial
scores on nodes storing feature data. In such case the
transmission of raw objects’ data is unnecessary.
Two message types are sent during query
execution. The request contains locations, their
current maximum possible values, preferences and
the current score of k-th best object. The response
comprises maximum possible values updated using
the results of partial value computation. The process
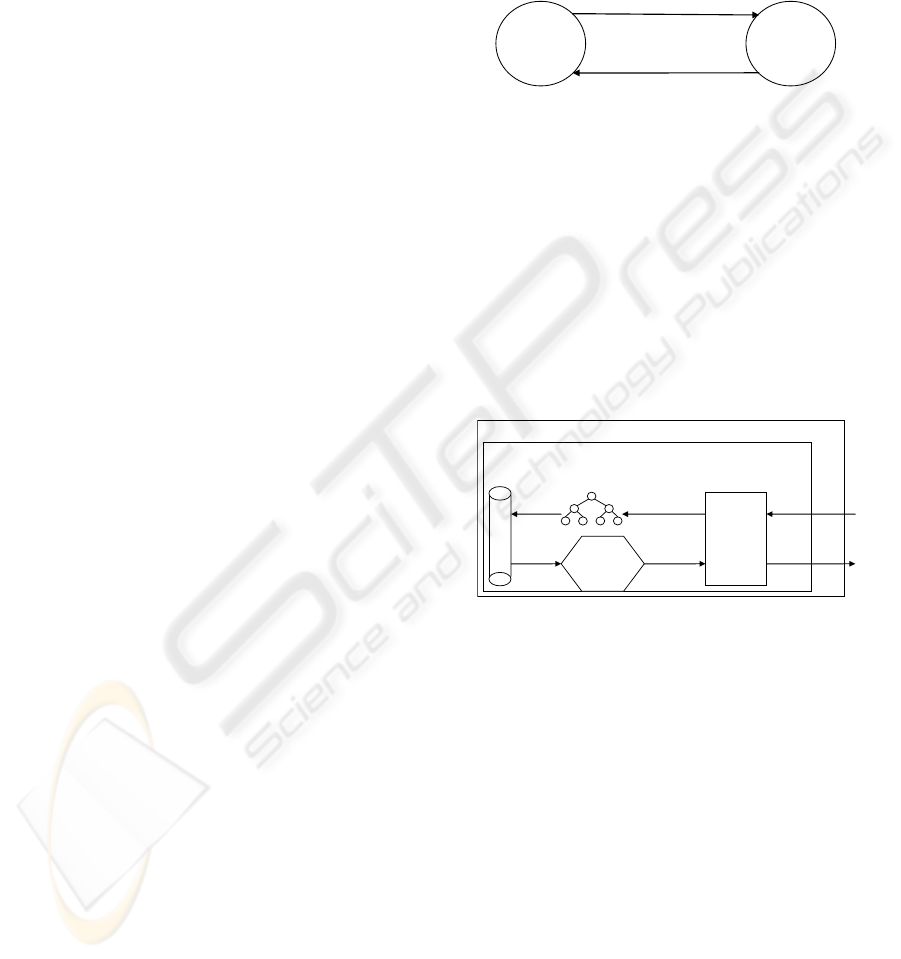
is presented on figure 2.
Updated maximum possible value t
+
(p)
Update maximum possible value of location p
Computer storing
target data set D
Computer storing
feature data sets
utilized by
preferences in P
on the basis of preferences’ set P.
Figure 2: Basic communication during query execution.
Such solution also ensures direct access to
indices during partial value computation and allows
to easily employ existing optimization methods.
Internal schema of updating maximum possible
value is presented on figure 3.
Query execution is therefore split in two parts.
The part executed on the node storing target data is
responsible for sending requests and finding objects
satisfying the query conditions to the greatest extent.
The part executed on nodes storing feature data
updates maximum possible values.
Computer storing feature data set F
c
Spatial index of
F
c
data set
Program updating maximum possible values of locations
Get objects
oid
1
,..,oid
n
Objects
o
1
,..,o
n
Find objects located
in the neighborhood
of p
Update t
+
(p)
basing on
attributes of
o
1
,...,o
n
Updated t
+
(p)
Communication
Laye
r
Response containing
the updated value of
t
+
(p)
A request to update
maximum possible
value t
+
(p) of
location p
Feature
data F
c
Figure 3: Update of location’s maximum possible score.
4 PARTIAL SCORE ALGORITHM
The implemented partial score computation
algorithm evaluates partial values of locations on the
basis of preferences defined in the request and uses
the values to update maximum possible scores of
locations. The algorithm employs existing R-tree
based optimization techniques during the process.
The pseudo code of the algorithm is presented as
algorithm 1. The algorithm utilizes either
GroupRNGValue or GroupNNValue algorithm
(presented as algorithms 2 and 3). They draw upon
the description of computing many objects’ values
simultaneously (Yiu et al., 2007). Additionally
GroupNNValue draws upon the nearest neighbour
search method presented in (Hjaltson and Samet,
1999).
ICEIS 2009 - International Conference on Enterprise Information Systems
44

Algorithm 1. Value Computation Algorithm updating maximum
possible partial values of locations.
1.Repeat:
2. Wait until value computation request is received.
3. Extract set P of preferences, set V of locations and
discarding value x from the request.
4. Group preferences f
c
∈
P into sets S
d
of similar
preferences.
5. Create list I containing sets S
d
ordered descending by
their cardinality.
6. For every S I:
i
∈
7. If f
c
∈
S define neighborhood using range method:
d
8. Compute partial values t
d
(p) of p
∈
V
executing GroupRNGValue(root of index
storing data utilized by f
c
∈
S
d
, V, range
parameter of f
c
∈
S , S ).
d d
9. Else if f
c
∈
S
d
define neighborhood using nearest
neighbor method:
10. Compute partial values t
d
(p) of p
∈
V
executing GroupNNValue(root of index storing
data utilized by f
c
∈
S
d
, V, S
d
).
11. For every p
∈
V:
12. Update maximum possible value t
+
(p) of p on
d
(p). the basis of t
t
+
13. If (p) ≤ x:
[object discarding] 14. Remove p from V.
15. Send a response containing t
+
(p) of current p
∈
V.
Algorithm 2. Algorithm GroupRNGValue simultaneously
computing partial values of locations using RNG search.
GroupRNGValue(node N of index storing feature data, set V
e d, similar preferences set S) of locations, rang
1.For every e
∈
N:
2. For every p
∈
V: [simultaneous computation of partial
values of many objects]
3. is a leaf:
If di ≤ d:
If N
4. stance between e.MBR and p
Get o5. bject g pointed by e:
If distance between g and p ≤ d: 6.
7. For every f
c
∈
S:
[simultaneous computation of
partial values based on
similar preferences]
8. Compute t
c
(p) based on
attribute c of object g,
specified by f
c
, and its
current value t
c
(p).
9. if N is not a leaf:
If di
Else
10. stance between e.MBR and p ≤ d:
, V, d, S). 11. Execute GroupRNGValue(e
12. Break.
Algorithm 3. Algorithm GroupNNValue simultaneously
computing partial values of locations using NN search.
GroupNNValue(root R of index storing feature data, set V of
locations, similar preferences set S)
∈
1. Create centroid C based on locations p V.
2. Create set T storing locations for which nearest
neighbor is not yet found and fill it with all p
∈
V.
3. Create a priority queue Q storing entries ordered by
om C. their distance fr
4. Insert R into Q.
Until5. T = Ø or Q = Ø:
from Q. 6. Remove e = Q.first
If e 7. is an object
8. For every p
∈
T: [simultaneous computation
of pa
:
rtial values of many objects]
9. If minimal distance p.mindist between p
and a feature object is unknown or
p.mindist ≥ distance between p and e:
10. p.mindist = distance between p and
e.
11. For every f
c
∈
S: [simultaneous
computation of partial values
based on similar preferences]
12. Compute t
c
(p) based on
attribute c of object e,
specified by f
c
, and its
current value t
c
(p).
13. If distance between Q.first and C >
distance between p and C + p.mindist:
14. Remove
Else
p from T.
15. if e is a leaf:
object pointed by e into Q. 16. Insert
17. Else:
For e
∈
18. very y e:
19. Insert y into Q.
5 SCHEDULING ALGORITHM
In (Braun et al., 2001) and (Munir et al., 2008)
various scheduling algorithms for distributed
environment are presented. The problem of
scheduling requests in case of distributed top-k
spatial query computation, where several conditions
have to be met is however specific. This has driven
development of a specialized DMDL (Distributed
Mixed Dynamic Leveled) scheduling algorithm. The
algorithm controls query execution by managing the
schema of sending requests. It is also responsible for
finding query results on the basis of data received in
responses.
5.1 Requests
One of the features of the DMDL algorithm is the
method of choosing locations sent in one request.
Each request contains locations of objects stored in
one R-tree leaf. Such solution is characterized by a
higher ratio of processing time spent on value
computation to time spent on managing the
messages than the ratio of a schema where each
request contains e.g. one location.
The technique has many other advantages. It
allows efficient utilization of the optimization based
on discarding objects, which is not possible when
requests contain a large number of locations. For
example, when each request contain all locations, it
is impossible to utilize the technique as no total
score is known before all partial values are
computed. To utilize the discarding technique each
request contains the score of k-th best object, which
allows discarding objects on nodes computing
partial values and further reducing transmitted data.
The solution also allows to utilize the
optimization based on simultaneous computation of
partial values of objects stored in one R-tree leaf.
Another feature of the algorithm is grouping
preferences by the node storing data on which they
depend on. Each request contains all preferences
based on data stored on its target node. In effect,
computing scores of objects from one leaf requires
that communication between node storing target data
and each node storing utilized feature data occurs
once. Otherwise it would be equal to the number of
preferences based on data sets stored on the node. It
allows to reduce the number of exchanged messages.
5.2 Scheduling Schema
The DMDL algorithm utilizes parallel processing in
a manner appropriate for the specifics of top-k
ALGORITHMS FOR EFFICIENT TOP-K SPATIAL PREFERENCE QUERY EXECUTION IN A HETEROGENEOUS
DISTRIBUTED ENVIRONMENT
45

spatial preference queries. It simultaneously
computes different partial values of objects from
different leaves, while partial scores of objects from
one leaf are computed serially. This results in
computing partial scores in a parallel manner and
simultaneously allows to utilize object discarding
technique, which in order to be efficient requires the
knowledge of previously computed partial scores.
The algorithm also aims at maximizing the level
of parallel processing, as it strives to it guarantee
that at any moment each node has at least two
requests to process. After sending a response to one
of them it can instantly start processing the other.
The algorithm also highly adapts itself to the
environment in which it is being executed. Its
schema of sending requests depends on the time of
computing partial scores on remote nodes and the
distribution of requests on the nodes. It uses a
register of the number of requests on each node and
sends eah request first to the node which did not yet
compute the partial values of the objects it concerns
and is characterized by the lowest number of waiting
requests. This solution generally gives higher
priority to nodes processing requests fast which
results in optimizing execution by discarding objects
before sending requests to nodes computing partial
scores slowly. As the mechanism is not based on
any constants describing the execution environment
the algorithm automatically adapts itself to changes
occuring in the observed node efficiency.
It has to be noted that predicting the optimal
order of computing partial values is not trivial. There
are many factors that influence the time between
sending the request and receiving the response.
Apart from character of preferences and data, it is
influenced by availibility of resources and network
capacity. Furthermore, the times of computing
partial values on different nodes can change as their
load and network’s capacity is dynamic.
Another mechanism employed by the algorithm
strives to balance the number of requests on all
nodes. If more than six requests are waiting on any
of the nodes then no new requests concerning
objects from not yet analyzed R-tree leaves are sent.
It prevents an undesirable effect from occuring. It
developes in environments in which the time of
processing requests on different nodes is heavily
varied. In such case new requests concerning not yet
analyzed object sets are constantly sent to fast nodes,
while a very low number of objects’ total scores is
known. It results in not discarding many objects
because of a relatively low score of k-th best object
at the time of sending new requests. Requests being
later sent to slower nodes contain larger number of
locations and the total execution time is significantly
increased. The employed technique adjusts the level
of parallel processing for the discarding technique to
be efficient in any execution environment.
The pseudo code of this algorithm is presented as
algorithm 4.
Algorithm 4. Request Sending algorithm DMDL.
DMDL
1.Repeat:
2. Wait until query execution request is received.
3. Extract preferences f
c
, k parameter and information
about target data set from the request.
4. Locate the root R of index storing target data.
5. Create list L containing sets P
e
of preferences f
c
based on data stored on one remote node.
6. Create list W of currently analyzed target object
sets.
7. Create a min-heap D storing objects ordered by score.
8. Create variable s = 0 storing the number of already
analyzed leaves.
9. Repeat until s = R.leafnum and W = Ø:
10. If W ≠ Ø:
11. Wait until a response is received.
12. Get the object set V
x
∈
W concerned by the
response.
13. Decrement P
e
.numexec of P
e
concerned by the
response.
14. For every p
∈
V :
x
15. If response contains t (p):
+
16. Update maximum possible value of p
using t (p).
+
17. Else:
18. Remove p from V
x
.
19. If objects’ p
∈
V
x
partial values are
computed for all preference sets P
e
∈
L:
20. For every p
∈
V :
x
21. If D.size < k or t(p) >
t(D.first):
22. Insert p into D.
23. If D.size > k:
24. Remove D.first from D.
25. Remove V from W.
x
26. Else:
27. If V
x
≠ Ø:
28. Get preference set P
e
∈
L, not used
yet to compute partial values of
objects from V
x
and which
P .numexec is lowest.
e
29. Send partial value computation
request concerning objects from V
x
set to the remote node storing
data utilized by f
∈
P .
c e
30. If all preference sets’ P
∈
L, P
e
.numexec <6:
e
31. For every preference set P
∈
L:
e
: 32. While P
e
.numexec < 2 and s < R.leafnum
33. Create set V
x
containing objects
stored at s+1 leaf of R tree.
34. Send a partial value computation
request concerning objects from V
x
set to the remote node storing
by f
c
∈
P
e
. data utilized
35. Increment s.
36. Increment P
e
.numexec.
37. Send a query response containing description of
objects stored in D.
It sends requests concerning objects from
different R-tree leaves to different nodes
participating in query execution. After receiving
each response the scores of the objects are updated
and the next request concerning these objects is sent
to the next node which did not compute the partial
values of the objects yet and is characterized by the
lowest number of requests. After receiving each
response the algorithm checks if any there are more
than six requests on any of the nodes. If it does not
ICEIS 2009 - International Conference on Enterprise Information Systems
46

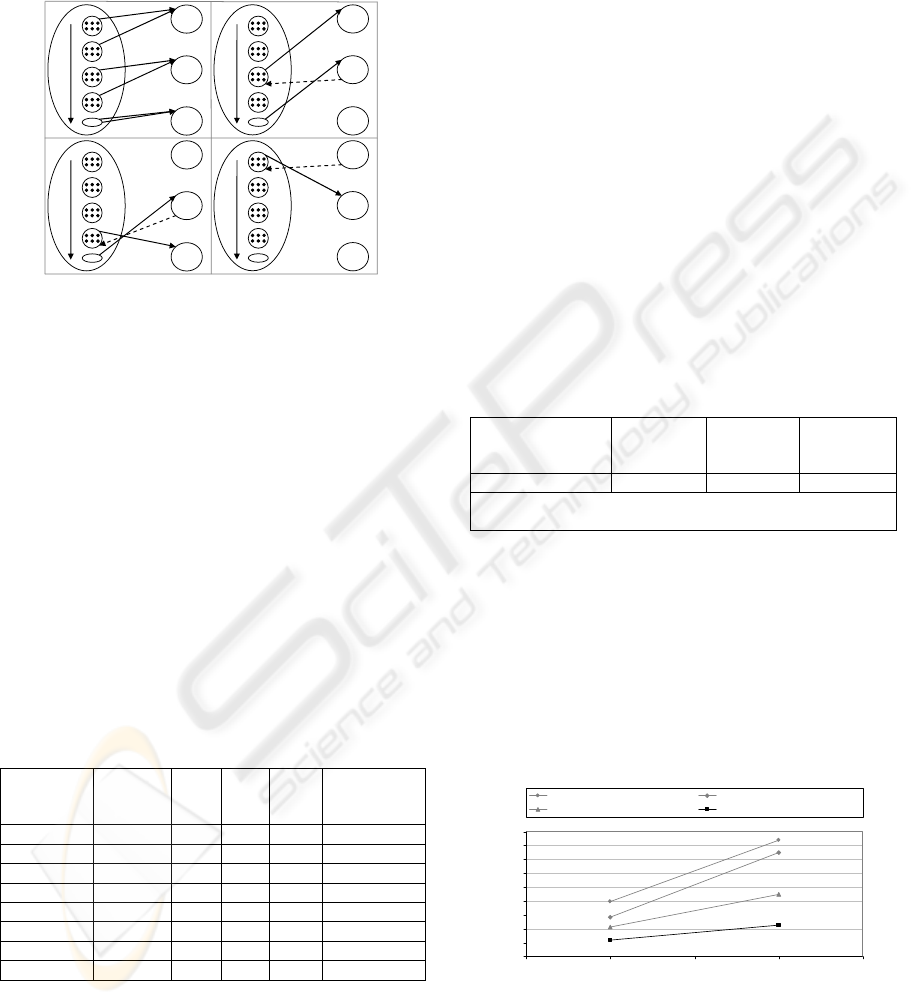
find any it instantly sends new requests concerning
objects from not yet analyzed R-tree leaves to all
nodes with less than two requests. The process ends
after computing total scores of all objects, which
were not discarded thus yielding the best-k objects.
cfd
f
1
...
f
c
f
d
...
f
f
cfd
f
g
...
f
i
cfd
ctd
A
B
C
D
1 2
cfd
f
1
...
f
c
f
d
...
f
f
cfd
f
g
...
f
i
cfd
ctd
A
B
C
D
cfd
f
1
...
f
c
f
d
...
f
f
cfd
f
g
...
f
i
cfd
ctd
A
B
C
D
3
cfd
f
1
...
f
c
f
d
...
f
f
cfd
f
g
...
f
i
cfd
ctd
A
B
C
D
4
AB
CD
EF
ABC
DG
EF
ABC
GH
EFD
BC
GHA
EFD
Figure 4: DMDL algorithm’s execution schema.
Figure 4 presents the schema of this algorithm.
The node storing target data is labeled as “ctd” and
nodes storing feature data are labeled as “cfd”. Sets
of objects from one leaf are presented as circles
containing dots. Solid lines represent requests and
dashed lines represent responses.
6 ALGORITM’S EFFICIENCY
In order to examine the efficiency of DMDL
algorithm an experiment was conducted aiming at
comparing it to algorithms realizing the queries on
locally available data. Such algorithms do not
require data transmission and have access to all
information about the query execution process.
Table 1: Preferences of the executed query.
Neighbor-
hood
Definition
Data
Set
Attri-
bute
Range
Value
Computation
Method
Preference 1 NN F
1a
p1 N/A N/A
Preference 2 NN F
1b
p2 N/A N/A
Preference 3 NN F
2
p1 N/A N/A
Preference 4 NN F
2
p2 N/A N/A
Preference 5 RNG F
3
p1 3 maximum
Preference 6 RNG F
3
p2 3 maximum
Preference 7 RNG F
4
p1 3 maximum
Preference 8 RNG F
4
p2 3 maximum
The experiment based on executing a query
moderately prone to all optimization techniques
implemented in score computation algorithm. It
searches for the objects from set D which satisfy the
conditions presented in table 1 to the greatest extent.
Four of the preferences define the neighborhood of
the object as its nearest neighbor (NN) and four
classify all objects located within some specified
distance from the object as its neighbors (RNG). The
conditions are based on attributes of objects from
differetn data sets. The distance parameter of all
range preferences equals 3 units and they utilize the
highest attribute value of objects from the area as a
base for the partial score.
To realize the comparison the query was being
executed by DMDL and L1P1S1 (Gorawski and
Dowlaszewicz, 2008.09) algorithms. The experiment
based on an assumption that three computers are
available. First, the distributed application was setup
on the computers as described by table 2 and
employed to execute the query. Later, assuming that
it would be possible to aggregate the data required
by the query, each of the computers was used to
execute the query using L1P1S1 algorithm. The
cardinality of utilized data sets equalled 10000 and
20000.
Table 2: Character of the distributed environment.
Configuration Intel
Pentium M
1,7GHz
Intel Core 2
Duo
1,83GHz
AMD Duron
1,6GHz
distributed system aF
1
aD, aF
3
, pF
4
aF
2
(75%)
aX
[y]
: application responsible for operating on data sets X
[y[n]]
(XX%): percent of generated artificial processor load
Figure 5 presents the results. In the test case the
distributed algorithm executed the query in
significantly shorter time than the local algorithm,
despite the need of data transmission. It stems from
the fact that the algorithm not only minimizes
transmitted data and utilizes existing optimization
techniques, but also further optimizes the execution.
Also, further rise of data sets’ cardinality resulted in
increasing DMDL’s relative performance.
0
5
10
15
20
25
30
35
40
45
5000 10000 15000 20000 25000
time [s]
AMD Duron 1,6GHz 640MB RAM Intel Pentium M 1,7GHz 1,5GB RAM
Intel Core 2 Duo 1,83GHz 1,5GB RAM distributed system
Figure 5: Time of query execution using local L1P1S1 and
distributed DMDL algorithm for data sets’ cardinality
equal 10000 and 20000 objects.
Another experiment concerned executing the
query while generating artificial load on one of the
ALGORITHMS FOR EFFICIENT TOP-K SPATIAL PREFERENCE QUERY EXECUTION IN A HETEROGENEOUS
DISTRIBUTED ENVIRONMENT
47

computers. The load modelled a different process.
The cardinality of data sets utilized during this
experiment equalled 20000. The results are
presented on figure 6.
In the future we consider extending the query
definition possibilities. One of the possible upgrades
is defining an area in which the query is executed.
This is a straightforward modification, which can
leverage the functionality and substantially reduce
the time required to obtain relevant results.
The experiment proved that executing queries in
a distributed environment is much more efficient
when the computers comprising the system are
simultaneously used for other tasks. It can utilize
computers shared by many queries less frequently
and move the main processing effort to computers
specific for each query. Such behaviour is
particularly desired when many queries are executed
in parallel.
REFERENCES
Yiu, M., L., Dai, X., Mamoulis, N., Vaitis, M. ‘Top-k
Spatial Preference Queries’, In proceedings of
International Conference on Data Engineering,
Istanbul, Turkey, 2007, pp. 1076 – 1085.
Guttman, A. ‘R-trees: A Dynamic Index Structure for
Spatial Searching’, In proceedings of ACM SIGMOD
International Conference on Management of Data,
Boston, USA, 1984, pp. 47 – 57.
0
50
100
150
200
250
no load 75% load
time [s]
AMD Duron 1,6GHz 640MB RAM Intel Pentium M 1,7GHz 1,5GB RAM
Intel Core 2 Duo 1,83GHz 1,5GB RAM distributed system
Gorawski, M., Dowlaszewicz, K. ‘Optimization of Top-k
Spatial Preference Queries’ Execution Process Based
on Similarity of Preferences’, In proceedings of
International Conference on Multimedia & Network
Information Systems, Wrocław, Poland, 2008.09, pp.
140 – 151.
Güntzer, U., Balke, W-t., Kießling W. ‘Towards Efficient
Multi-feature Queries in Heterogeneous
Environments’, In proceedings of International
Conference on Information Technology: Coding and
Computing, Las Vegas, USA, 2001, pp. 622 – 628.
Figure 6: Time of query execution using local L1P1S1 and
distributed DMDL algorithm while generating artificial
load on one of the computers.
Michel, S., Triantafillou, P., Weikum, G. ‘KLEE: A
Framework for Distributed Top-k Query Algorithms’,
In proceedings of International Conference on Very
Large Data Bases, Trondheim, Norway, 2005, pp. 637
– 648.
7 SUMMARY AND OUTLOOK
The paper presents a proposition of an algorithm for
execution of top-k spatial preference queries in a
distributed environment. The specifics of the query
and the target environment necessitated developing
adequate mechanisms that would ensure efficient
execution. Data processing was therefore split on all
nodes taking part in query execution and the number
of data transmitted through the network was
minimized. Apart from that further optimization
mechanisms were introduced. The paper discussed
both the specifics that motivated the development of
each technique and the technique itself. It also
presents an analysis of algorithm’s efficiency based
on conducted experiments. The results confirm that
the DMDL algorithm, which employs an efficient
auto adaptation method is capable of efficient
executing the queries in a heterogeneous distributed
environment. It can be utilized in a closed dedicated
system or in an open system comprising different
computers owned by different parties. The
experiments also proved that data can be distributed
on purpose in order to shorten the time of executing
complex top-k spatial preference by employing the
developed algorithm.
Bruno, N., Gravano, L., Marian, A. ‘Evaluating Top-k
Queries over Web-Accessible Databases’, In
proceedings of International Conference on Data
Engineering, San Jose, USA, 2002, pp. 369 – 380.
Gorawski, M., Dowlaszewicz, K. ‘: An Analysis and
Extension of Top-K Spatial Preference Queries
Optimization Methods’, In proceedings of
International Conference on Information Technology,
Gdańsk, Poland, 2008.05, pp. 227 – 230.
Hjaltson, G., R., Samet, H. ‘Distance Browsing in Spatial
Databases’, ACM Transactions on Database Systems,
vol. 24, issue 2, June 1999, pp. 265 – 318.
Braun, T., D., Siegel H., J., Beck, N., Bölöni, L.,
Maheswaran, M., Reuther, A. I., Robertson, J., P.,
Theys, M., D., Yao, B., Hensgen, D., Freund, R., F. ‘A
Comparison of Eleven Static Heuristics for Mapping a
Class of Independent Tasks onto Heterogeneous
Distributed Computing Systems’, Parallel and
Distributed Computing, vol. 61, 2001, pp. 810 – 837.
Munir, E., U., Li, J., Shi, S., Zou, Z., Yang, D. ‘MaxStd: A
Task Scheduling Heuristic for Heterogeneous
Computing Environment’, Information Technology
Journal, vol. 7, issue 4, 2008, pp. 679 – 683.
ICEIS 2009 - International Conference on Enterprise Information Systems
48