
ANT PAGERANK ALGORITHM
Mahmoud Zaki Abdo, Manal Ahmed Ismail
Communciation Dept. Faculty of Engineering, Helwan Uninersity, Cairo, Egypt
Mohamed Ibraheem Eladawy
Communciation Dept. Faculty of Engineering, Helwan Uninersity, Cairo, Egypt
Keywords: Search engine, PageRank algorithm, Ranking algorithms, Ant algorithm.
Abstract: The amount of global information in the World Wide Web is growing at an incredible rate. Millions of
results are returned from search engines. The rank of pages in the search engines is very important. One of
the basic rank algorithms is PageRank algorithm. This paper proposes an enhancement of PageRank
algorithm to speed up the computational process. The enhancement of PageRank algorithm depends on
using the Ant algorithm. On average, this technique yields about 7.5 out of ten relevant pages to the query
topic, and the total time reduced by 19.9 %.
1 INTRODUCTION
The amount of information on the web is growing
rapidly, as well as the number of new users
inexperienced in the art of web search engine.
World Wide Web search engines have become the
most heavily used online services, with millions of
searches performed each day (B. Davision, 2000).
The web search engines use the structure present in
hypertext to provide much higher quality search
results (S. Brain, 1998).
The rank of pages is an integral component of
any search engine. In the context of the web search
engines, the role of ranking becomes even more
important. The most important researches proposing
Link Analysis Ranking (A. Borodin, 2005) are
found in Kleinberg (J. Kleinberg, 1999), and Brin
and Page (S. Brain, 1998).
Link Analysis Ranking can be described as the
use of hyperlink structure for the purpose of ranking
web documents. Link Analysis Ranking operates on
the graph representation of hyperlinked web
documents. The hyperlink graph is based on the
representation of a web page as a node and
hyperlink between pages as a directed edge. The
goal of Link Analysis Ranking is to extract this
information, and use it to determine a particular
weight for every page, and use these weights to rank
the web documents. This paper proposes an
enhancement to speed up the computation of
PageRank algorithm (S. Brain, 1998) by using Ant
algorithm.
The rest of the paper is organized as follows.
Section two presents an overview on the Link
Analysis Ranking Algorithms. Section three
explains Ant System. Section four explains the
proposed Ant PageRank algorithm. Section five
presents the experimental data preparation. Section
six presents experimental results. Finally, Section
seven concludes the paper.
2 LINK ANALYSIS RANKING
ALGORITHMS
All the Link Analysis Ranking algorithms start with
a collection of Web pages to be ranked. These
algorithms proceed as follows:
Extraction: extracting the hyperlinks between
the pages
Construction: constructing the underlying
hyperlink graph. The hyperlink graph is
constructed by creating a node for every Web
page, and a directed edge for every hyperlink
between two pages.
Calculation of Node Weight: The graph is
given as input to the Link Analysis Ranking
algorithms. The algorithms operate on the
73
Zaki Abdo M., Ahmed Ismail M. and Ibraheem Eladawy M. (2009).
ANT PAGERANK ALGORITHM.
In Proceedings of the 11th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
74-80
DOI: 10.5220/0001863400740080
Copyright
c
SciTePress
graph, and calculate a weight for each Web
page. This weight is used to rank the pages.
In the following two subsections; the In-degree
algorithm (P. Tasparas, 2004) and PageRank
algorithm (S. Brain, 1998) will be briefly described
as examples of Link Analysis Ranking algorithms.
2.1 In-degree Algorithm
The In-degree algorithm depends on the popularity
of pages. The number of pages that link to this page
measures the popularity of a page. It ranks pages
according to their in-degree pages (the number of
pages that link to the page).
2.2 The PageRank Algorithm
The algorithm depends on the computation of the
PageRank weight of all pages in the graph by Eq.
(1). The PageRank weight of a page A is given as
follows:
1
(1)
1
where:
- PR (A) is the PageRank weight of the page A.
- Page A has pages T
1
, T
2
... T
n
which point to it,
as shown in Figure 1.
- The parameter d is a damping factor which can
be set between (0, 1); usually set d to 0.85.
- C (T) is the number of links going out of page
T.
- B (A) the set of nodes that point to node A
(Backwards links).
Figure 1: The PageRank graph.
The intuition underlying the In-degree algorithm
is that a page has a good weight is a page that is
pointed to by many nodes in the graph. Brin and
Page (S. Brain, 1998) extended this idea further by
observing that not all pages have the same weight.
Links from pages of high quality should confer more
weight. It is not only important how many pages
point to a page, but also what the quality (value of
the page weight ) of these pages is.
Therefore, Brin and Page (S. Brain, 1998) had
proposed a one-level weight propagation scheme,
where a page has a good weight is the one that is
pointed by many pages have a good weights. Figure
2 shows the PageRank algorithm.
Due to the huge size of actual web, an
approximate iterative computation is usually applied
to calculate the PageRank weight. This means that
each page is assigned an initial starting value and the
PageRank weights of all pages are then calculated in
several computation circles based on Eq. (1). The
minimum PageRank of a page is given by (1 - d);
while the maximum PageRank is determined as dN
+ (1 - d), where N is the number of pages. This
maximum PageRank weight can theoretically
achieved, only when all web pages solely link to one
page, and this page also solely links to itself (Nan
Ma, 2008).
Figure 2: PageRank Algorithm.
W
1
2
3
123
11
0…
0…1
01
0…
1…1
1
1
1
0
0
0
1
1
1
…
…
…
1
1
1
…
…
…
1
0
0
The PageRank algorithm uses a matrix W to
represent the hyperlink graph. where:
• Matrix W represents the hyperlink graph
- “1” in row i and column j means that page
j points to page i.
- “0” in row i and column j means that page
j does not point to page i.
• Matrix W is N * N, where N is the number of
nodes.
Page
A
Page
T
1
Page
T
2
Page
T
n
PR
i
1d
d
PRj
Cj
B
PageRank Algorithm
Initialize all PageRank weights to 1
Repeat until the PageRank weights are convergent
For every node i
ICEIS 2009 - International Conference on Enterprise Information Systems
74

3 ANT SYSTEMS
Ant System introduced by Dorigo (Dorigo, 1991).
Dorigo's artificial ants (called ants) have some major
differences with real (natural). First, ants have a
memory. Second, ants are not completely blind.
While natural ants rely on chemical signals to
navigate. Finally, due to obvious constraints
imposed by the architecture of current computers,
artificial ants live in a world where time is discrete
(Islam, 2005). In the case of Travel salesman
Problem (TSP)
- Ants have a memory; this memory is used to
store a list of previously visited cities.
- Ants are not completely blind. Ants are aware
of the distance between cites.
To examine the ant algorithms, apply them to the
well-known travelling salesman problem (TSP) (E.
L. Lawler, 1985)
3.1 Ant System and Travel Salesman
Problem (TSP)
Given a set of n towns, the TSP problem can be
stated as the problem of finding a minimal length
closed tour that visits each town once. The distance
between town i and town j is calculated by
Euclidean distance equation (2).
x
x
y
y
(2)
An instance of the TSP problem is given by a
weighted graph (N,E), where N is the set of towns
and E is the set of edges between towns, weighted
by the distances. assume b
t
i1,...,n is the
number of ants in town i at time t. Then the total
number of ants is calculated by equation (3)
m
∑
b
t
(3)
Each ant is a simple agent with the following
characteristics:
• When going from town i to town j it lays a
substance, called trail, on edge (i,j);
• It chooses the town to go to with a probability
that is a function of the town distance and of the
amount of trail present on the connecting edge.
• Each ant has a data structure, called a tabu list.
That memorizes the towns already visited up to
time t and forbids the ant to visit them again
before a tour has been completed. When a tour is
completed the tabu list is emptied and the ant is
free again to choose its way. The vector
containing the tabu list of the k-th ant is tabu
k
and tabu
k
(s) is the s-th element of the tabu list of
the k-th ant. Let
(t) be the intensity of trail on
edge (i,j) at time t. At each iteration of the
algorithm trail intensity becomes
τ
t1
ρ.τ
t
∆τ
t,t 1
(4)
where ρ is a coefficient such that 1 ρ represents
the evaporation of trail. The coefficient ρ must be set
to a value <1 to avoid unlimited accumulation of
trail
∆τ
t,t 1
∑
∆τ
t,t 1
(5)
where ∆τ
t,t 1 is the quantity per unit of length
of trail substance (pheromone in real ants) laid on
edge (i,j) by the k-th ant between time t and t+1.
The transition probability from town i to town j for
the k-th ant is
p
t
τ
α
.η
β
∑
τ
α
.η
β
if j allowed
0 otherwise
(6)
where allowed = {j is not in tabu
k
} and η
is the
visibility of town j from town i, which is simply the
value 1/ d
ij
. Where
α and β are parameters that allow
a user to control the relative importance of trail
versus visibility. Therefore the transition probability
is a tradeoff between visibility (which says that close
towns should be chosen with high probability) and
trail intensity (that says that if on edge (i,j) there has
been a lot of traffic then it is highly desirable, thus
implementing the autocatalytic process).
Different choices about how to compute ∆τ
t,t
1
and when to update the τ
t
cause different
Instantiations of the ant algorithm. In the next two
sections Dorigo (Dorigo, 1991) present the three
approaches. Dorigo (Dorigo, 1991) used as
experimental test-bed for ideas, namely Ant-density,
Ant-quantity, and Ant-cycle.
3.2 The Ant-density and Ant-quantity
Approaches
Initially, two approaches where developed by
Dorigo (Dorigo, 2000) to exploit his Ant System
heuristic named : Ant-density and Ant-quantity. In
the Ant-density approach a quantity Q1 of trail for
every unit of length is left on edge (i,j) every time an
ant goes from i to j; in the Ant-quantity approach an
ant going from i to j leaves a quantity Q2/dij of trail
for every unit of length.
ANT PAGERANK ALGORITHM
75
Therefore, in the Ant-density approach
∆τ
t,t 1
1
0
(7)
And in the Ant-quantity approach
∆τ
t,t 1
1
0
(8)
where: Q
1
and Q
2
are the same quantity of
pheromone. Thus, an increase in trail intensity on
edge (i,j) when an ant goes from i to j is independent
of dij in the Ant-density approach and is inversely
proportional to dij in the Ant-quantity approach (i.e.,
shorter edges are made more desirable by ants in the
Ant-quantity approach, thus further reinforcing the
visibility factor in equation (6)).
3.3 The Ant-cycle Approach
The approach introduced a major difference with
respect to the two previous systems. Here ∆τ
is not
computed at every step, but after a complete tour (n
steps). The value of ∆τ
(t,t+n) is given by
∆τ
,
,
0
(9)
where Q3 is a constant and L
k
is the tour length of
the k-th ant. The entire Ant-Cycle approach is
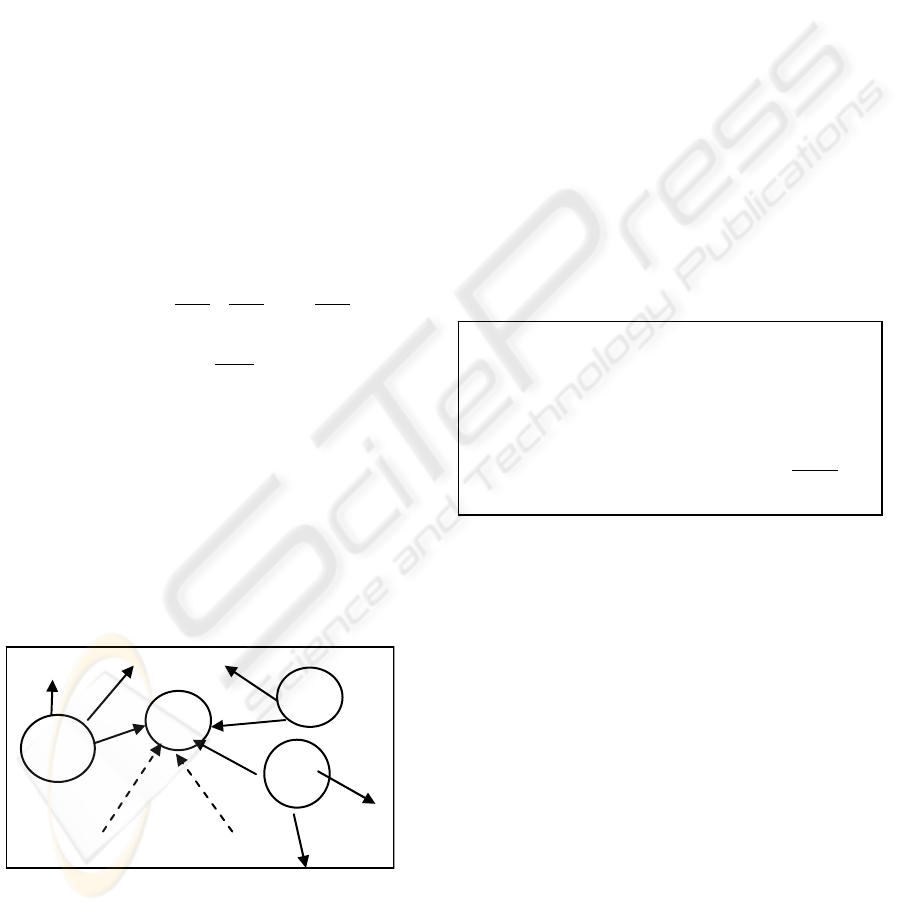
demonstrated in (Islam, 2005)
Figure 3: The Path of one ant with high in-degree selected
from out-degree pages.
4 PROPOSED ANT PAGERANK
ALGORITHM
The main objective behind Ant PageRank algorithm
is reducing the execution time for computing the
PageRank weight of the pages. The PageRank
weight of the page depends on the weight of the in-
degree pages as shown in equation (1). The proposed
algorithm locates ants in the pages without in-degree
pages, and release the ant move on the graph (as
Figure 3) and calculate the PageRank weight of the
pages in the tabu of the ant.
The ant moves to one page from out-degree page.
This paper introduces novel PageRank approaches to
be used the conjunction with the Ant algorithm.
1- Ant PageRank approach 1: Locate one ant in
every page without in-degree pages. The ant
moves to one page from out-degree pages as
random selected.
2- Ant PageRank approach 2: Locate one ant in
every page without in-degree pages. The ant
moves to one page from out-degree page as high
in-degree page selected.
3- Ant PageRank approach 3: Locate two ants in
every page without in-degree pages. Every ant
move to one page from out-degree page as
random selected.
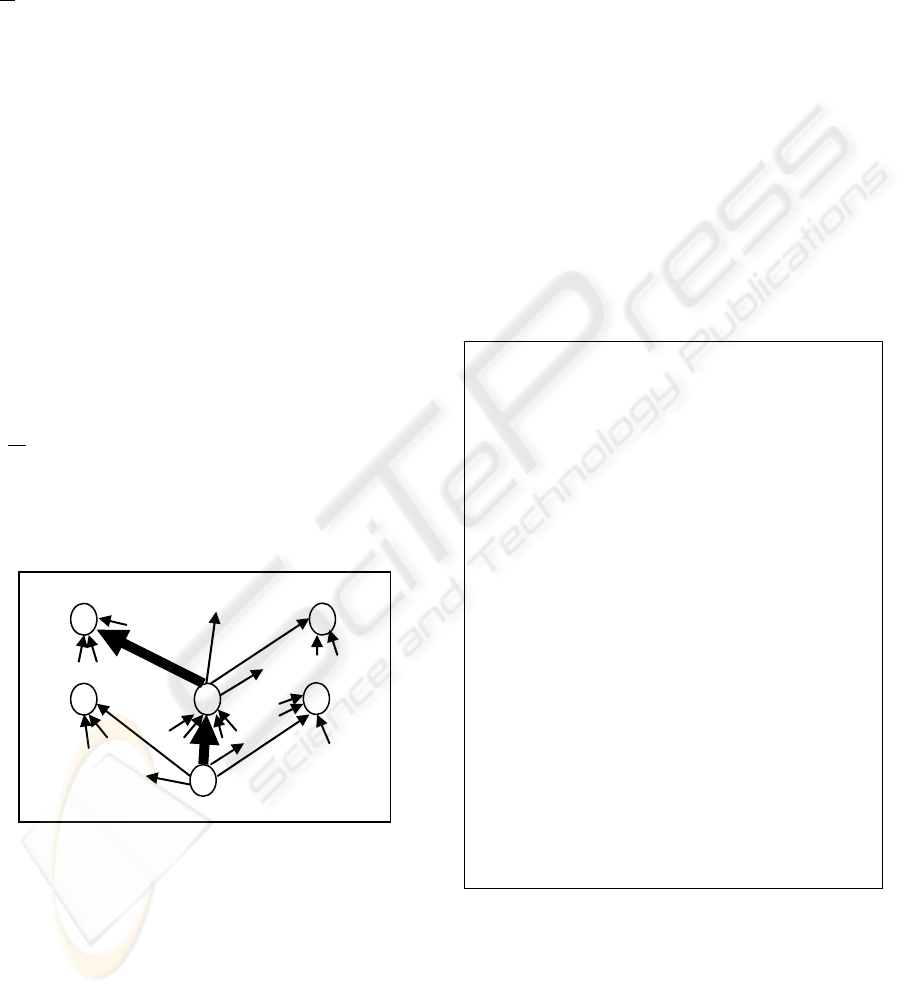
Figure 4: Ant PageRank algorithm.
Figure 4 shows the Ant PageRank algorithm. The
algorithm divided into three approaches:
- Approach 1: Locate one ant in every page
without in-degree and select the next page as
random.
- Approach 2: Locate one ant in every page
without in-degree and select the next page as
A
D
E
F
C
B
1. Place N ant on every page without In-degree Pages.
- Approach 1: N=one Ant
- Approach 2: N=one Ant
- Approach 3: N=two Ant
2. Every ant will start its tour by selecting the next
page to be visiting from out-degree pages as:
- Approach 1: Random
- Approach 2: Higher in-degree pages
- Approach 3: Random
3. Add next page visited to the ant’s tabu list.
4. Repeat step 2 for every ant until the page being
visit exists in the ant story (a cycle is found) or visit
the page without out-degree Page.
5. When step 4 is completed, applying the equation
(1) of the element in every ant’s tabu list.
6. After step 5 is completed the voting determine the
best pages
7. Return the top ten pages.
ICEIS 2009 - International Conference on Enterprise Information Systems
76

higher in-degree page.
- Approach 3: Locate two ants in every page
without in-degree and select the page as
random.
The change of the number of ants and the method of
selecting the next page of the ant are used to get the
best time and high top ten pages for matching of the
result in the PageRank algorithm.
5 EXPERIMENTAL DATA
PREPARATION
This section presents a brief description of
experimental results of the proposed algorithm. The
experimental results data are text files (
P.Tsaparas,
2008). These text files contain information about
queries used in the experimental phase. These text
files represent the following 33 queries namely:
"abortion", "affirmative action", "alcohol",
"amusement parks", "architecture", "armstrong",
"automobile industries", "basketball", "blues",
"cheese", "classical guitar", "complexity",
"computational complexity", "computational
geometry", "death penalty", "genetic",
"geometry", "globalization", "gun control", "iraq
war", "jaguar", "Jordan", "movies", "national
parks", "net censorship", "randomized
algorithms", "recipes", "roswell", "search
engines", "shakespeare", "table tennis", "vintage
cars", "weather".
Each query represented by three text files named
"nodes", "adj_list", and “inv_adj_list".
The nodes.txt file is formatted as follows:
• Number of pages
• Information of each page, each page is
described as follows [Page ID, http address of
the page, page title, number of in-degree
pages, Number of out-degree pages]
The Adjacency List file contains a list of out-degree
page IDs for each page. An example of a page entry
can be describes as follow:
1:20 500 6
This means that the page with ID= 1, points to the
pages with IDs = {20, 500, 6}.
The Inverted Adjacency List file contains a list of
in-degree page IDs for each page. An example of a
page entry can be describes as follow:
20:1 5 80 -1
This means that the page with ID =20, is pointed to
by the pages with IDs = {1, 5, 80}.
Table 1: Array of structure to represents the data of the
graph.
Node 1
ID
Node 1
Indegree
Number
Node 1
Outdegree
Number
[ ]
Node 1
Indegree
[ ]
Node 1
Outdegree
Node 2
ID
Node 2
Indegree
Number
Node 2
Outdegree
Number
[ ]
Node 2
Indegree
[ ]
Node 2
Outdegree
… … … … …
… … … … …
… … … … …
Node
N ID
Node N
Indegree
Number
Node N
Outdegree
Number
[ ]
Node N
Indegree
[ ]
Node N
Outdegree
The implementation steps of the proposed algorithm
are detailed as follow:
1- Data preprocessing step.
2- Executing proposed algorithm.
3- Comparing the results.
The preprocessing step includes the creation of an
array of structure to represent the data. The structure
is as follows:
NodeID: a unique identifier for the Page
NodeIndegreeNumber: Number of in-degree
Pages
NodeOutdegreeNumber: Number of out-
degree Pages
[ ] NodeIndegree: Array of NodeID of in-
degree pages
[ ] NodeOutdegree: Array of NodeID of out-
degree pages
where: Length of the array is number of pages.
Table 1 shows this structure. This structure only
needs to store ID of in-degree pages and ID of out-
degree pages of each node. This structure replaced
by the matrix
nn
W
*
used in the classical PageRank
algorithm as explained in subsection 2-2.
6 EXPERIMENTAL RESULTS
This section illustrates experiment results of the
proposed algorithm. The experiments done by
running the proposed algorithm on the 33 query
illustrated in section 5. The comparison between the
proposed algorithm and the classical PageRank
algorithm depends on the following factors:
• Number of memory cells used.
• Number of iteration for each query.
• Total computation time.
• Number of pages matched in top ten pages with
the classical PageRank algorithm.
ANT PAGERANK ALGORITHM
77
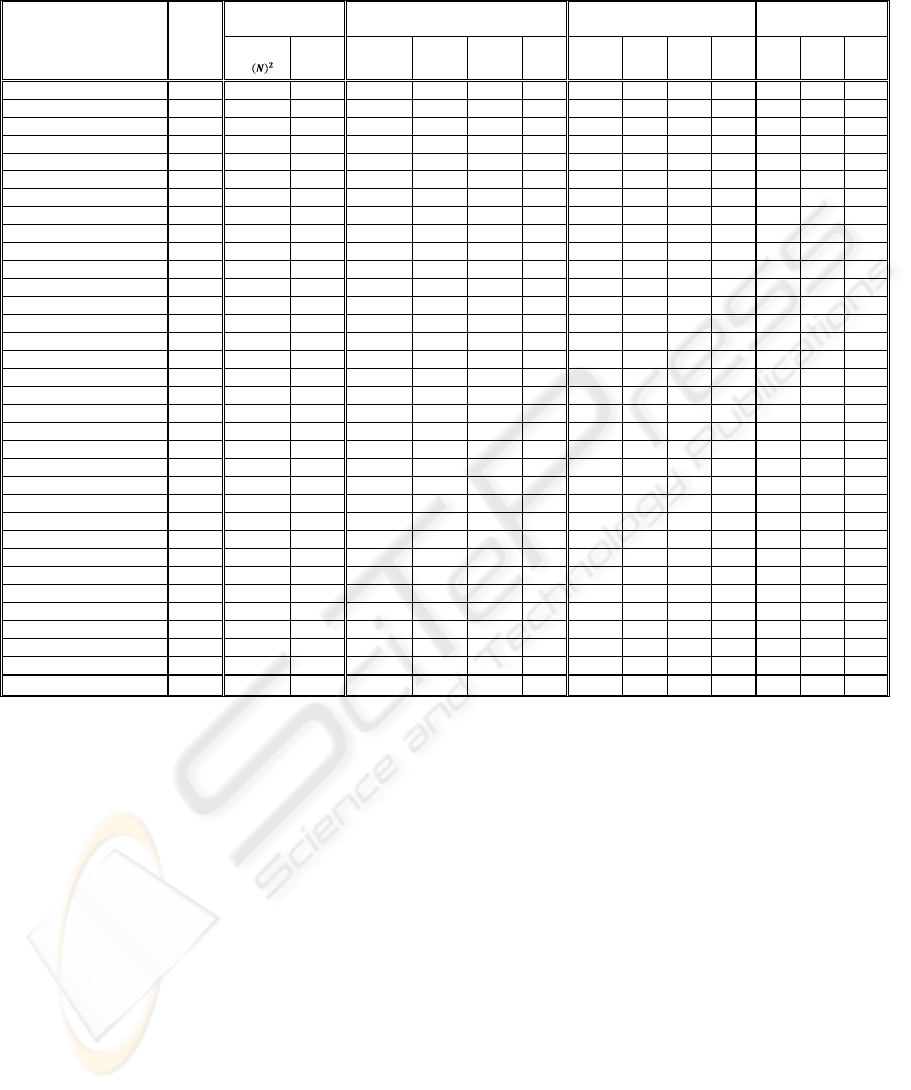
Table 2: Memory used, total number of iterations, computation time, and number of pages matched for classical PageRank
algorithm versus Ant PageRank algorithm approaches.
Table 2 compares the results of both algorithms in
terms of memory used, number of iteration,
computation time, and number of pages matched
with classical PageRank algorithm.
The main contributions of the proposed
algorithm are:
The percentage in average of the memory used in
the proposed Ant PageRank algorithm versus
conventional PageRank algorithm is 0.2 %. The
memory used in the classical PageRank
algorithm is N
2
, while the memory used in the
proposed algorithm is based on the number of in-
degree pages and the number of out-degree pages
as shown in Table 1.
The percentage in average of the number of
iteration in all pages in the classical PageRank
algorithm versus Ant PageRank algorithms are
(as shown in Table 2):
- Ant PageRank algorithm approach 1 reduces
the number of iteration by 95.5 %.
- Ant PageRank algorithm approach 2 reduces
the number of iteration by 96.1 %.
- Ant PageRank algorithm approach 3 reduces
the number of iteration by 93.9 %.
The average of the computation time in all pages
in the classical PageRank algorithm versus Ant
algorithms are (as shown in Table 2):
- Ant PageRank algorithm approach 1 reduces
the computation time by 19.9 %.
- Ant PageRank algorithm approach 2 reduces
the computation time by 21.5 %.
- Ant PageRank algorithm approach 3 reduces
the computation time by 18.7 %.
The average top ten pages results are matched
with the classical PageRank algorithm in each
approach are (as shown in Table 2):
- Ant PageRank algorithm approach 1 is 7.5 pages.
- Ant PageRank algorithm approach 2 is 6.9 pages.
- Ant PageRank algorithm approach 3 is 7.5 pages.
Query
Numbe
r of
Pages
( N )
Memory used
( Cell )
Number of iteration Computation time (Sec)
Number of pages
matched with PR alg.
PR alg. Ant PR
alg.
PR alg.
Ant
PR1
Ant
PR2
Ant
PR3
PR alg.
Ant
PR1
Ant
PR2
Ant
PR3
Ant
PR1
Ant
PR2
Ant
PR3
abortion 3340 11155600 44574 163660
5147 4287 6952
0.70
0.59 0.55 0.61 8 8 8
affirmative action 2523 6365529 9314 131196
4431 3910 6109
0.41
0.30 0.25 0.30 9 7 10
alcohol 4594 21104836 33342 220512
9642 10575 14248
1.016
0.86 0.80 0.90 8 8 8
amusement parks 3410 11628100 21160 153450
4106 3448 5397
0.66
0.64 0.55 0.61 4 4 4
architecture 7399 54745201 72242 369950
12484 10830 17668
2.58
3.02 4.02 2.97 4 4 5
automobile industries 1196 1430416 6114 52624
1875 1394 2121
0.11
0.09 0.10 0.11 9 8 9
armstrong 3225 10400625 16318 148350
6255 5686 9431
0.55
0.45 0.38 0.48 8 7 8
basketball 6049 36590401 48818 229862
12293 10256 17003
2.06
1.58 1.46 1.58 8 8 8
blues 5354 28665316 48778 256992
10250 8586 14447
1.47
1.25 1.141 1.28 8 8 9
cheese 3266 10666756 23320 150236
6526 5653 8935
0.56
0.55 0.48 0.55 4 6 4
classical guitar 3150 9922500 24088 113400
5314 4509 7326
0.56
0.52 0.44 0.53 5 5 5
complexity 3564 12702096 26962 128304
5139 3857 6542
0.80
0.61 0.53 0.61 7 7 6
computational complexity 1075 1155625 4362 38700
1504 1226 2022
0.09
0.078 0.06 0.11 8 8 8
computational geometry 2292 5253264 16378 38964
3373 2683 4385
0.36
0.30 0.23 0.28 7 7 7
death penalty 4298 18472804 43912 171920
6194 5015 8157
1.36
0.77 0.64 0.78 8 7 8
Genetic 5298 28068804 38522 227814
10581 10041 15229
1.48
1.15 1.03 1.19 8 5 8
Geometry 4326 18714276 26726 211974
7386 6478 10045
1.14
0.84 0.73 0.86 8 8 8
globalization 4334 18783556 34848 216700
6533 5884 9040
1.14
0.89 0.75 0.86 6 5 7
gun control 2955 8732025 23476 153660
4756 3801 6203
0.61
0.45 0.41 0.45 8 8 8
iraq war 3782 14303524 30746 158844
5899 4876 7467
0.84
0.63 0.52 0.63 7 7 7
Jaguar 2820 7952400 16784 141000
5516 4826 7905
0.48
0.36 0.31 0.39 8 8 9
Jordan 4009 16072081 21874 200450
7799 7192 11646
0.73
0.61 0.55 0.66 8 7 8
Movies 7967 63473089 57628 294779
15754 13425 22601
3.45
2.87 2.73 2.86 8 8 7
national parks 4757 22629049 28312 228336
10148 8927 14843
1.18
0.81 0.80 0.86 7 7 8
net censorship 2598 6749604 15776 124704
3927 3402 5059
0.47
0.39 0.36 0.38 8 8 8
randomized algorithms 742 550564 2410 6678
1128 1070 1631
0.0625
0.05 0.14 0.078 9 9 9
Recipes 5243 27489049 36304 272636
10540 9445 15251
1.31
1.13 1.11 1.16 9 7 8
Roswell 2790 7784100 16974 150660
4641 4153 6304
0.5
0.41 0.47 0.42 7 4 7
search engines
11659 135932281
584472 524655
17023 12981 22428
9.73
6.88 6.55 6.77 8 8 7
shakespeare 4383 19210689 27150 219150
8758 8347 12714
0.98
0.72 0.72 0.80 9 7 9
table tennis 1948 3794704 10930 54544
3440 2788 4575
0.25
0.22 0.28 0.23 7 7 7
vintage cars 3460 11971600 25592 148780
4739 3810 6523
0.64
0.64 0.64 0.64 6 4 5
Weather 8011 64176121 69344 376517
18947 14601 27233
3.59
2.94 0.64 3.06 10 8 10
percentage in average 100 0.2 100
4.5 3.9 6.1
100
80.1 78.5 77.3 7.5 6.8 7.5
ICEIS 2009 - International Conference on Enterprise Information Systems
78

7 CONCLUSIONS
This paper has proposed the Ant PageRank
algorithm. This algorithm has a flexible parameters
to control the behaviour of the Ant algorithm. These
can be achieved through three approaches, which are
proposed to enhance the classical PageRank
algorithm. The enhancement is based on two factors,
computation time and memory required.
As demonstrated, the top ten pages which are
achieved by the proposed algorithm are matched
with the top ten pages of the classical PageRank
algorithm, with lower execution time, number of
memory cells, and number of iteration. Presents
The best experimental is Ant PageRank
algorithm experimental 1. This experimental use one
ant with random selected. This experimental reduces
the percentage in average execution time by 19.9%
and matches with 7.5 pages from top ten pages with
classical PageRank algorithm.
REFERENCES
A. Borodin, G. O. Roberts, J. S. Rosenthal, and P.
Tsaparas. Link Analysis Ranking Algorithms Theory
and Experiments”. ACM Transactions on Internet
Technologies, ,Vol. 5, No. 1, Pages 231–297,
February 2005
Dorigo Marco, Vittorio Meniezzo, and Alberto Colorni.
“Positive Feedback as a Search Strategy”, Technical
report n91-016. Department of Electronics, Milan
Polytechnic Institute, June 1991.
Dorigo Marco, Eric Bonabeau, and Guy Theraulaz. “Ant
Algorithms and Stigmergy”, future Generation
Computer System, 16(2000), 851-871.
E.L.Lawler, J.K.Lenstra, A.H.G.Rinnooy-Kan,
D.B.Shmoys eds., The Travelling Salesman Problem,
New York:Wiley, 1985.
Islam A.Elgawad “ Development in web search engine
optimization “, M.sc Thesis, Computers and
Information - Helwan university, 2005
J. Kleinberg. “Authoritative sources in a hyperlinked
environment”. Journal of ACM (JASM), vol. 46,
pages 604-632, 1999.
Nan Ma,Jiancheng Guan,Yi Zhao. "Bringing PageRank to
the citation analysis”, Information Processing &
Management, Volume 44, Issue 2, 2008, Pages 800-
810.
P. Tsaparas (2004), “Link Analysis Ranking”, Ph.D
Thesis, University of Toronto, March 2004.
P.Tsaparas(2008)“http://www.cs.toronto.edu/~tsap/experi
ments/download/download.html”
S. Brin and L. Page, “The anatomy of a large-scale hyper
textual Web search engine”. In Proceedings of the 7th
International World Wide Web Conference, Brisbane,
Australia, 1998.
ANT PAGERANK ALGORITHM
79
