Evolving System’s Modeling and Simulation through

Reﬂective Petri Nets

Lorenzo Capra and Walter Cazzola

Department of Informatics and Communication

Universit

a degli Studi di Milano, Italy

Abstract. The design of dynamic discrete-event systems calls for adequate mod-

eling formalisms and tools to manage possible changes occurring during system’s

lifecycle. A common approach is to pollute design with details that do not regard

the current system behavior rather its evolution. That hampers analysis, reuse

and maintenance in general. A reﬂective Petri net model (based on classical Petri

nets) was recently proposed to support dynamic discrete-event system’s design,

and was applied to dynamic workﬂow’s management. Behind there is the idea that

keeping functional aspects separated from evolutionary ones and applying them

to the (current) system only when necessary, results in a simple formal model on

which the ability of verifying properties typical of Petri nets is preserved. In this

paper we provide the reﬂective Petri nets with a (labeled) state-transition graph

semantics.

1 Introduction

Most existing discrete-event systems are subject to evolution during their lifecycle.

As an example consider of mobile ad-hoc networks, adaptable software, business pro-

cesses, and so on. Designing dynamic discrete-event systems calls for adequate model-

ing formalisms and tools. Unfortunately, well-established formalisms for discrete-event

systems, such as classical Petri nets [10], lack features for naturally expressing possible

run-time changes to system’s structure. An approach commonly followed consists of

polluting system’s functional aspects with details concerning evolution. This practice

hampers system analysis, reuse and maintenance.

Reﬂective Petri nets [3] were recently proposed as a formal model for dynamic

discrete-event systems. This approach is based on a reﬂective layout formed by two

logical levels. The achieved clean separation between functional and evolutionary con-

cerns results in a simple formal model for systems exhibiting a high dynamism in which

the analysis capabilities of classical Petri nets should be preserved. Reﬂective nets were

successfully applied to specify dynamic workﬂows [2, 4], in which the workﬂow’s tem-

plate can change according to business needs. On the line of [9], the approach imple-

ments a smart transfer mechanisms of running workﬂow instances on the modiﬁed pro-

cess template, which prevents already completed, bypassable tasks from being redone

from scratch. It relies on checking the preservation of structural Petri net properties that

permit an efﬁcient characterization of workﬂow’s soundness [12] over the time.

Capra L. and Cazzola W. (2009).

Evolving System’s Modeling and Simulation through Reﬂective Petri Nets.

In Proceedings of the 4th International Conference on Evaluation of Novel Approaches to Software Engineering - Evaluation of Novel Approaches to

Software Engineering, pages 59-70

DOI: 10.5220/0001955300590070

 SciTePress

On the perspective of implementing an automatic solver and a discrete-event sim-

ulation engine, Reﬂective Petri nets are provided in this paper with a (labeled) state-

transition semantics. Any analysis/simulation techniques based on state-space inspec-

tion has to face a crucial question, that is how to recognize possible equivalent states

during base-level’s evolution. That major topic is managed by exploiting the symbolic

state (marking) deﬁnition that the particular ﬂavor of Colored Petri nets [8] used for the

meta-level is provided with, and represents the paper’s main technical contribution.

The balance of the paper is as follows: background information are in sections 2,3,

where the focus is put there on those elements directly connected to the paper’s contri-

bution, which is presented in section 4 where the state-transition semantics for Reﬂec-

tive Petri nets is deﬁned. An application to an instance of dynamic system is presented in

section 5. Finally section 6 is about work-in-progress. Assuming the readers have some

basic knowledge about Petri nets, a semi-formal presentation is adopted, and a simple

example is used. Unessential notions\notations are skipped, especially in introductory

parts.

2 WN Basics

The formalisms employed for the two layers (meta- and base-level) of the reﬂective lay-

out are Well-formed Nets (WN) [6], a ﬂavor of Colored Petri nets (CPN) [8], and their

unfolding, an extension of ordinary Place/Transition nets [10] respectively. This choice

has revealed convenient for two main reasons: i) the behavior of reﬂective Petri nets can

be formally stated in terms of classical Petri nets; ii) the symbolic state representation

the WN formalism is provided with leads to an effective state-transition semantics for

Reﬂective Petri nets, in which the intriguing question related to recognition of equiv-

alent evolutions is efﬁciently handled.ding, an extension of ordinary Place/Transition

nets [10] respectively. This choice has revealed convenient for two main reasons: i) the

behavior of reﬂective Petri nets can be formally stated in terms of classical Petri nets; ii)

the symbolic state representation the WN formalism is provided with leads to an effec-

tive state-transition semantics for Reﬂective Petri nets, in which the intriguing question

related to recognition of equivalent evolutions is efﬁciently handled.

There is also a third reason, which is interesting in the perspective of doing perfor-

mance analysis: our feeling is that if we considered the stochastic extension of WNs

(SWN) [5], and their unfolding, that is Generalized Stochastic Petri nets (GSPN) [1],

for the meta- and base-level, we might set a timing semantics for Reﬂective Petri nets

inherited in large part from the GSPN (SWN) timing semantics (which is deﬁned in

terms of a Markov process). In the sequel of this work only the untimed behavior of

Reﬂective Petri nets will be deﬁned.

While retaining CPN’s expressive power, WNs are characterized by a structured

syntax which is used by efﬁcient analysis algorithms, based on the symbolic marking

notion. This section does not present all the features of WNs, for which the reader is

suggested to look at the original work, but just introduces them informally, focusing on

the symbolic marking deﬁnition.

Unlike CPNs, WNs (and their unfolding as well) include transition priorities and in-

hibitor arcs. Both these features enhance the CPN formalism expressiveness. In partic-

ular, priorities are useful to represent the transactional execution of evolutionary strate-

gies, as well as the implicit synchronization between base- and meta-level.

Because of the structured syntax of WN color annotations, behavioral symmetries

can be automatically discovered and exploited to build an aggregate state space (called

symbolic reachability graph or SRG) and (in SWN) a corresponding lumped Continu-

ous Time Markov Chain (CTMC).

2.1 WN Color Annotations

In Colored Petri nets places, as well as transitions, are associated to color domains,

i.e., tokens in places have an identiﬁer (color), similarly transitions are parameterized,

so that different color instances of a given transition can be considered. A marking

M maps each place p to a multiset on the corresponding color domain C(p). Any arc

connecting p to a transition t is labeled by a function mapping any element of C(t) (i.e.,

any color instance of t) to a multiset on C(p).

The peculiar and interesting feature of the WN formalism is the ability of captur-

ing system’s symmetries thanks to the structured syntax of color annotations. Efﬁcient

analysis/simulation algorithms can be applied that exploit such symmetries. These al-

gorithms rely upon the notion of symbolic marking (SM).

SWN color domains are deﬁned as Cartesian products of basic color classes C

that may be in turn partitioned into static subclasses C

i,k

. A SM provides a syntactical

equivalence relation on ordinary colored markings: two markings belong to the same

SM if and only if they can be obtained from each other by means of permutations on

color classes that preserve static subclasses. A SM is formally expressed in terms of

dynamic subclasses.

2.2 The Symbolic Marking (SM) Notion

The deﬁnition of a SM (denoted

M) [6] comprises two parts specifying the so called

dynamic subclasses and the distribution of colored symbolic tokens (tuples built of

dynamic subclasses) over the net places, respectively.

Dynamic subclasses deﬁne a parametric partition of color classes preserving static

subclasses: let D

and s

denote the set of dynamic subclass of C

(in

M), and the

number of static subclasses of C

(if C

is not split then s

= 1). The j-th dynamic

subclass of C

, Z

∈ D

, refers to a static subclass, denoted d(Z

), 1 ≤ d(Z

) ≤ s

and has an associated cardinality |Z

|, i.e., it represents a parametric set of colors (in

the sequel we shall consider cardinality one dynamic subclasses). It must hold, for each

k : 1...s

j:d(Z

)=k



= | C

i,k

The token distribution in

M is deﬁned by a function (denoted itself

M) mapping

each place p to a multiset on the symbolic color domain of p, obtained replacing each

with D

in C(p).

Among several possible equivalent representations, the canonical representative [6]

provides SM with a univocal formal expression, based on a lexicographic ordering of

dynamic subclass distribution over the net places.

guards checking

begin strategies

strategies

Reﬂective Framework

Shift Up Action

Base Level Petri Net

Evolutionary Meta-Program

Evolutionary Interface

Base-Level Reiﬁcation

newP

delP

newT

ext_ev

start up

ext_ev

true

shift-down

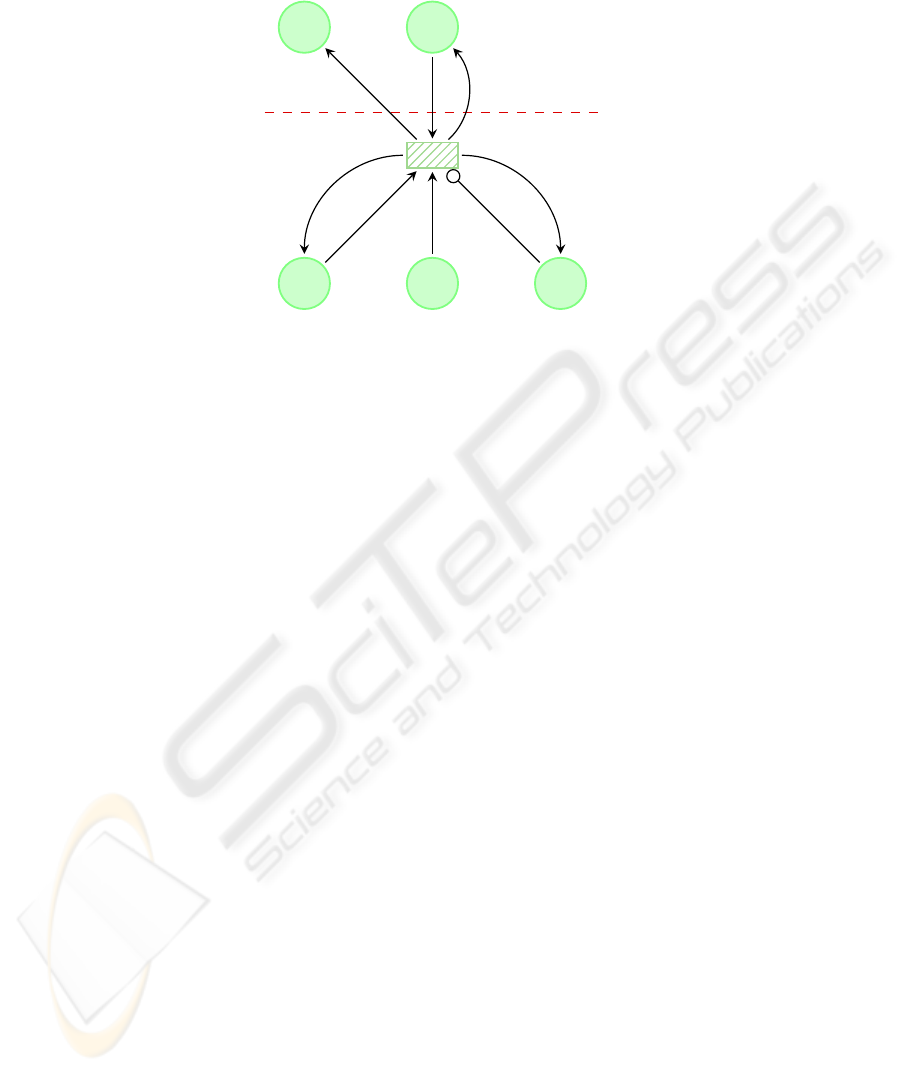
Fig. 1. Snapshot of the reﬂective PN model.

3 Reﬂective Petri Nets

The reﬂective Petri net approach permits developers to model a discrete-event system

and separately its possible evolutions, and to dynamically adapt system’s model when

evolution occurs.

The approach is based on a reﬂective architecture structured in two logical layers

(Fig. 1). The ﬁrst one, called base-level, is an ordinary Petri net (a P/T net with priori-

ties and inhibitor arcs) representing the system prone to evolve (base-level PN); while

the second layer, called meta-level, consists of a high-level Petri net (a colored Petri

net) representing the evolutionary strategies (the meta-program, following the reﬂec-

tion parlance) that drive the evolution of the base-level when certain conditions/events

occur.

Meta-level computations in fact operate on a representative of the base-level, called

(base-level) reiﬁcation. The reiﬁcation is deﬁned as a (high-level Petri net) marking,

whose a portion, encoding the base-level PN current state (marking), is updated ev-

ery time the base level Petri net enters a new state. The reiﬁcation is used by the

meta-program to observe (introspection) and manipulate (intercession) the base-level

PN. Any change to the reiﬁcation is reﬂected to the base-level at the end of a meta-

computation (shift-down action)

The meta-program is implicitly activated (shift-up action) and then a suitable strat-

egy is put into action, under two conditions: i) either when it is triggered by an external

event, or ii) when the base-level enters a given state.

The reﬂective framework, a high-level Petri net component as well, is responsible

for really carrying out the base-level evolution in a transparent way. It should be con-

sidered as a transparent (meta-)layer of the reﬂective model, therefore it is formed by

higher-priority transitions. Intercession on the base-level PN is carried out in terms of

a minimal but complete set of basic operations (called the evolutionary interface): ad-

dition/removal of places, transitions, arcs - change of transition priorities (base-level’s

NODE

reifM

base-level petri net

meta-level petri net

<S p

>+2<S x

<S p

ShUp|shift-up

Fig. 2. Reiﬁcation implemented at Petri nets level.

structure change), free moving tokens overall the base-level PN places (base-level’s

state change). If one such operation reveals inconsistent, the meta-program is restarted

and any change caused in the meanwhile to the base-level reiﬁcation is discarded. In

other words, evolutionary strategies have a transactional semantics. After a strategy’s

succeeding execution, changes are reﬂected down to the base-level Petri net.

Developers have been provided with a tiny ad-hoc language, inspired to Hoare’s

CSP that allows anybody to specify his own strategy in a simple way, without any

skills in high-level Petri net modeling being required. An automatic translation to a

corresponding high-level Petri net is done. Several strategies could be candidate for

execution at a given instant: different policies might be adopted in that case to select

one, ranging from a deterministic choice to a static assignment of priorities.

According to the reﬂective paradigm, the base-level runs irrespective of the meta-

program, being even not aware of its existence. That raises consistency issues, that are

faced by determining, for any strategies, local inﬂuence areas on the base-level that are

temporarily locked by the meta-level while strategies are being executed.

The interaction between base- and meta- levels, and between meta-level entities, is

formalized in [3]. Let us only outline some essential points:

1. The structure of the reﬂective framework is ﬁxed, while the evolutionary strategies

are coupled to the base-level PN, so they vary from time to time. More precisely, the

meta-program’s model is built according to a predeﬁned pattern, whose strategies

represent the variable component.

2. The reﬂective framework and the meta-program are separated (high-level Petri

net) components, sharing two disjoint sets of boundary places denoted hereafter

reiﬁcation-set and evolutionary interface, respectively. Their composition through

a simple place superposition rises to the meta-model, called hereafter meta-level

PN.

3. The reiﬁcation-set is formed by the following colored places: reifN, reifA,

reifΠ, reifM. The corresponding color domains, which will be speciﬁed later,

are built of basic color class Node, a logically unbounded repository holding all po-

tential base-level nodes, considering any evolutions. A well-deﬁned marking of the

set above, hereafter simply denoted reiﬁcation, encodes the structure (i.e., nodes,

arc connections and transition priorities, respectively), and the current marking, of

the base-level PN. What is the most important, there is a one-to-one correspon-

dence, formalized by a bijection, between reiﬁcations and P/T nets.

4. The initial reiﬁcation, from time to time, refers to the base-level Petri net modeling

the initial system conﬁguration.

5. The shift-up action and the reiﬁcation update after any base-level change of state,

are implemented in transparent way at net level, by suitably connecting any base-

level PN transition to place reifM , that holds the reiﬁcation of base-level PN’s

current marking. The resulting model will be hereafter denoted base-meta PN. The

idea is illustrated in Fig. 2. Any changes of state at the base-level Petri net are

instantaneously reproduced on the reiﬁcation, conceptually maintaining base-level

unawareness about the meta-program. As an example, the ﬁring of transition t

results in withdrawing one and two tokens from places p

and x

, respectively, and

putting one in p

. While token consumption is emulated by (input) arc function

hS p

i + 2 · hS x

i, token production is emulated by (output) arc function hS p

A complete splitting of class Node is required to refer to any places added to the

base-level (e.g., x

), by means of WN constant functions.

6. The shift-down action, i.e., the reﬂection of changes performed by the meta-program,

is modeled by a homonym highest-priority transition of the meta-level PN; it is a

kind of meta-transition that adheres to the usual ﬁring rule as concerns the meta-

level PN, further, it replaces the (current) base-level PN by the P/T net encoded by

the reiﬁcation.

The ﬁxed part of the reﬂective architecture (the reﬂective framework) is used to put

evolution into practice for any kind of system being modeled. It is responsible for the

reﬂective behavior of the architecture, hiding the work of the evolutionary component

to the base-level PN. This approach permits a clean separation between evolution and

evolving system, and prevents the base-level PN from being polluted by details related

to the evolution.

4 State-transition Semantics for Reﬂective PN

The adoption of WN formalism [6] for the meta-program permits an effective deﬁnition

of behavior, in terms of state-transitions. In particular, the WN symbolic marking notion

is exploited to identify equivalent states a Reﬂective Petri net model (possibly) reaches

during the evolution.

On the light of the causal connection established between base- and meta-level,

the behavior of a Reﬂective Petri net model between any meta-level activations is fully

described in terms of a WN model, the meta-level PN, which includes (better, is suitably

connected to) an uncolored part, the base-level PN. That model will be hereafter denoted

base-meta PN. Therefore, it comes to be natural providing Reﬂective Petri nets with the

notion of state below:

Deﬁnition 1 (State). A state of a Reﬂective Petri net is a marking M

of the base-meta

PN obtained by composing the base-level PN and the meta-level PN.

Letting t (6= shiftdown) be any transition (color instance) enabled in M

, ac-

cording to the classical Petri net’s ﬁring rule, and M

be the marking reached upon its

ﬁring, we have the labeled state-transition

−→ M

There is nothing to do but consider the case where m

is a marking enabling the

pseudo-transition shiftdown: then,

shiftdown

−→ M

being the marking of the base-meta PN obtained by ﬁrst replacing the (current)

base-level PN with that one which is isomorphic to the reiﬁcation marking (once it has

been suitably connected to the meta-level PN), then ﬁring shiftdown as it were an

ordinary transition.

4.1 Recognizing Equivalent Evolutions

The state-transition graph semantics just introduced precisely deﬁnes the (timed) be-

havior of a reﬂective Petri net model but suffers from two evident drawbacks. First, it

is highly inefﬁcient: the state description is exceedingly redundant, comprising a large

part concerning the meta-level PN which is unnecessary to describe the evolving sys-

tem. The second concern is even more critical and indirectly affects efﬁciency: there

is no way of recognizing whether the modeled system, during its dynamics/evolution,

reaches equivalent states. The ability of deciding about a system’s state-transition graph

ﬁniteness and strongly-connectedness (both issues being strictly related to the ability

of recognizing equivalent states) are in fact mandatory preconditions for performance

analysis: we know that a sufﬁcient condition for a ﬁnite CTMC to have stationary so-

lution (steady-state) is to include one maximal strongly connected component. More

generally, any technique based on state-space inspection relies on the ability above.

Recognizing equivalent evolutions is tricky. It may happen that (apparently) differ-

ent strategies cause in truth equivalent transformations to the base-level Petri net (the

evolving system), that cannot be identiﬁed by Def. 1. Yet, the combined effect of dif-

ferent sequences of evolutionary strategies might produce the same effects. Even more

likely, the internal dynamics of the evolving system might lead to reach equivalent con-

ﬁgurations. The above question, that falls into a graph isomorphism sub-problem, as

well as the global efﬁciency of the approach, are tackled by resorting to the peculiar

characteristic of WN: the symbolic marking notion. The color domains of the meta-

level PN are built of color class N ode, representing the base-level PN nodes (places

plus transitions) at the meta-level. As concerns the reiﬁcation-set, they are:

C(reifN ), C(reif M), C(reif ) : N ode

C(reifA) : N ode × N ode

Arcs are represented by 2-tuples belonging to N ode×Node, since there are no inhibitor

arcs in the running example (Fig. 3). Class Node is logically partitioned as follows:

named

z }| {

∪ . . . p

∪Unnamed

| {z }

places

∪

named

z }| {

∪ . . . t

∪Unnamed

| {z }

transitions

Symbols {p

}, {t

} denote singleton static subclasses. Conversely, Unnamed

and Unnamed

are static subclasses collecting all anonymous (i.e., indistinguishable)

places / transitions. The intuition behind is simple: while some (“named”) nodes, for

the particular role they play, preserve the identity during base-level evolution, and may

be explicitly referred to during base-level manipulation, others (“unnamed”) are indis-

tinguishable from each other. In other words any pair of “unnamed” places (transitions)

might be freely exchanged on the base-level PN, without altering the model’s semantics.

There are two extreme cases: named

(named

) = ∅ and, on the opposite, Unna−

med

(Unnamed

) = ∅. The former meaning that all places/transitions can be per-

muted, the latter instead that all nodes are distinct. Note that this static partition is dif-

ferent from that one actually used on the base-meta PN, where any places of base-level

PN must be explicitly referred to when connecting the base-level PN to the meta-level

PN (Fig. 2).

The technique we use to recognize equivalent base-level evolutions relies on the

base-level reiﬁcation and the adoption of a symbolic state representation for the base-

meta PN that, we recall, results from composing in transparent way the base-level PN

and the meta-level PN.

We only have to set as initial state of the Reﬂective Petri net model a symbolic

marking (

) of the base-meta PN, instead of an ordinary one: any dynamic subclass

of Unnamed

(Unnamed

) will represent an arbitrary “unnamed” place (transition)

of the base-level PN.

Because of the simultaneous update mechanism of the reiﬁcation and the conse-

quent one-to-one correspondence along the time between the current base-level PN and

its reiﬁcation at the meta-level, we can state the following:

Deﬁnition 2 (Equivalence Relation). let

be two symbolic states of the reﬂec-

tive Petri net model.

≡

if and only if their restrictions on the reiﬁcation set of

places have the same canonical representative.

Lemma 1. let

≡

. Then the base-level PNs at states

and

are isomor-

phic.

The transition between symbolic states of the reﬂective Petri net model is deﬁned

as follows.

Deﬁnition 3 (Symbolic State Transition). Let σ denote a (possibly empty) meta-level

PN’s transition ﬁring sequence, shiftdown /∈ σ. Then

−→

Fig. 3. Equivalent base-level Petri Nets.

iff t is either shiftdown or a base-level PN’s transition, and there exists σ,

−→

Of course

≡

, as well as any intermediate marking crossed by σ.

Consider the very simple example in Fig. 3, that depicts three base-level PN con-

ﬁgurations, at different time instants. The hypothesis is that while symbols t

denote

a “named” transition, symbols x

and y

denote “unnamed” places and transitions, re-

spectively. We assume that all transitions have the same priority level, so we disregard

the reiﬁcation of priorities.

We can observe that the Petri nets on the left and on the middle are the same, but for

their current marking: we can imagine that they represent a possible (internal) dynamics

of the base-level Petri net. Conversely, we might think of the right-most Petri net as an

(apparent) evolution of the base-level PN on the left, in which new connections and a

new marking are set.

Nevertheless, the three base-level conﬁgurations are equivalent, according to deﬁni-

tion 2. It is sufﬁcient to take a look at their respective reiﬁcations, encoded as symbolic

markings (multisets are expressed as formal sums): consider for instance the base-level

PN on the left and on the middle of Fig. 3, whose reiﬁcation are:

M(reifN) = y

+ y

+ t

+ x

M(reifM) = x

+ x

M(reifA) = hx

, t

i + ht

, x

i + hx

, y

i + hy

, x

i + hx

, t

i + ht

, x

i + hx

, y

i + hy

, x

and

(reifN) = y

+ y

+ t

+ x

(reifM) = x

+ x

(reifA) = hx

, t

i + ht

, x

i + hx

, y

i + hy

, x

i + hx

, t

i + ht

, x

i + hx

, y

i + hy

, x

respectively.

They can be obtained from each other by the following permutation of “unnamed”

places and transitions (we denote by a ↔ b the bidirectional mapping: a → b, b → a):

↔ x

, x

↔ x

, y

↔ y

thus, they are equivalent. With similar arguments we might show that the base-level

PN on the left and on the right of Fig. 3 are equivalent too. The right-hand Petri net’s

reiﬁcation is:

(reif N ) = y

+ y

+ t

+ x

(reif M ) = x

+ x

(reif A) = hx

, t

i + ht

, x

i + hx

, y

i + hy

, x

i + hx

, y

i + hy

, x

i + hx

, t

i + ht

, x

M and

can be obtained from each other by the following permutation:

↔ x

}

The canonical representative of these equivalent states is

5 Applying the Semantics

The (symbolic) state-transition semantics of Reﬂective Petri nets has been tested on the

hurried philosophers problem [11], a variant of the well known dining philosophers

problem that introduces a high dynamism and mobility degree: philosophers can join

and leave the table upon invitation. The version here considered meets the following

requirements:

– (at least) two philosophers are initially sitting at the table;

– each philosopher can eat only when he contemporary gets both adjacent forks, ac-

cording to the classical problem’s formulation;

– those philosophers sitting at the table that are not eating have the following addi-

tional capabilities:

• they can invite another philosopher (arbitrarily chosen) to join the table and sit

down at his side, if the table capacity has not been exceeded yet;

• they can ask one of the adjacent philosophers to leave the table (if more than

two are currently sitting);

– each philosopher is going around with his own fork; when he joins the table he

keeps the fork, when he leaves he brings the fork with him.

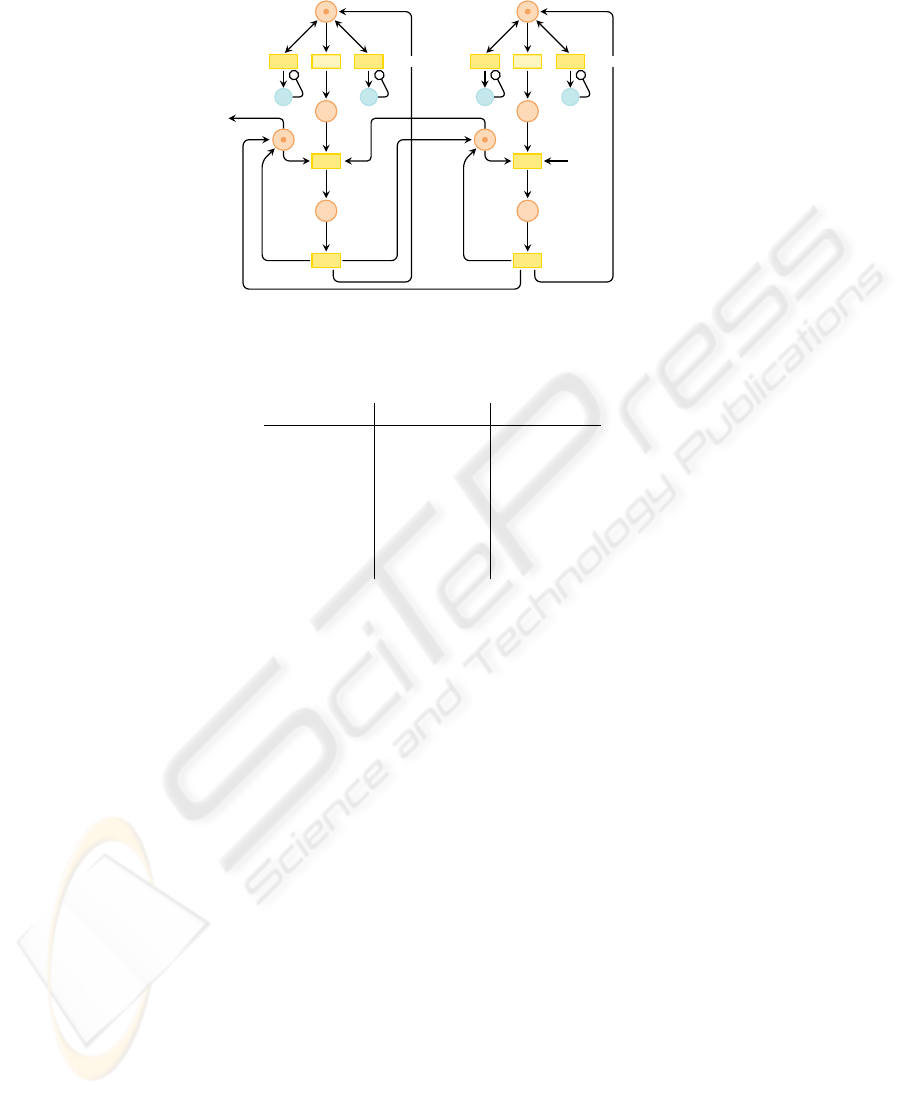
Figure 4 shows the base-level Petri net modeling the initial conﬁguration, where two

philosophers are sitting on the dining table. The invitation and chasing away capabili-

ties provoke the evolution of this simple model. Any arrivals/departures of philosophers

cause a local reconﬁguration of the system’s topology, that consists of carefully chang-

ing adjacencies and fork sharing in a consistent way. All that is completely managed at

meta-program level, as speciﬁed in [3].

Table 1 reports some evidences of the effectiveness of the symbolic state repre-

sentation adopted for Reﬂective Petri nets, versus the ordinary one. The experiment

was conducted using the GreatSPN tool and an ad-hoc script procedure emulating the

shift-down action. The ﬁrst column indicates the problem size, i.e., the table capacity.

All philosophers can be permuted with one another. We can appreciate a sensible re-

duction, even for small problem sizes, due to the very high symmetry degree exhibited

by the system during its evolution.

take fks

release fks

eat

think

invite

chase away

take fks

release fks

eat

think

invite

chase away

Fig. 4. Base-level Petri net modeling the initial hurried philosopher’s table.

Table 1. Symbolic vs. ordinary state-space size; — data not available.

# philosophers symbolic states ordinary states

3 423 2567

4 2843 374809

5 23560 1765836

6 147812 96905034

7 960345 —

8 4767385 —

9 12097086 —

6 Conclusions

We have semi-formally introduced a state-transition semantics for reﬂective Petri nets,

a formal layout based on classical Petri nets (Well formed Nets, and their unfolding)

well suited to model dynamic discrete-event systems. In particular, we have addressed

a major topic related to recognizing equivalent system’s evolutions, through the WN’s

symbolic state notion. We are planning to integrate the GreatSPN tool [7], that natively

supports WN (and their stochastic extension, SWN), with new modules (plug-in’s) for

the graphical editing and the analysis/simulation of reﬂective Petri net models. We are

studying the possibility of deﬁning a timed semantics for Reﬂective Petri nets, which

should be in large part inspired by SWN (GSPN) timed semantics. Finally, we are con-

sidering possible applications of reﬂective Petri nets for the simulation of protocols for

mobile, ad-hoc networks.

References

1. Ajmone Marsan, M., Conte, G., Balbo, G., 1984. A Class of Generalized Stochastic Petri

Nets for the Performance Evaluation of Multiprocessor Systems, ACM Transaction on Com-

puter Systems, bf 2, (2): 93–122.

2. Capra, L., Cazzola, W., 2007a. A Reﬂective PN-based Approach to Dynamic Workﬂow

Change, Proceedings of the 9th International Symposium in Symbolic and Numeric Algo-

rithms for Scientiﬁc Computing (SYNASC’07), IEEE, Timis¸oara, Romania, pp. 533–540.

3. Capra, L., Cazzola, W., 2007b. Self-Evolving Petri Nets, Journal of Universal Computer

Science, 13, (13): 2002–2034.

4. Capra, L., Cazzola, W., 2008. Evolutionary Design through Reﬂective Petri Nets: an Ap-

plication to Workﬂow, Proceedings of the IASTED International Conference on Software

Engineering (SE’08), Innsbruck, Aut.

5. Chiola, G., Dutheillet, C., Franceschinis, G., Haddad, S., 1993. Stochastic Well-Formed

Coloured Nets for Symmetric Modelling Applications, IEEE Transactions on Computers,

42, (11): 1343–1360.

6. Chiola, G., Dutheillet, C., Franceschinis, G., Haddad, S., 1997. A Symbolic Reachability

Graph for Coloured Petri Nets, Theoretical Computer Science B (Logic, Semantics and The-

ory of Programming), 176, (1& 2): 39–65.

7. Chiola, G., Franceschinis, G., Gaeta, R., Ribaudo, M., 1995. GreatSPN 1.7: GRaphical

Editor and Analyzer for Timed and Stochastic Petri Nets, Performance Evaluation, 24, (1-

2): 47–68.

8. Jensen, K., Rozenberg, G. (eds), 1991. High-Level Petri Nets: Theory and Applications,

Springer-Verlag.

9. Qiu, Z.-M., Wong, Y. S., 2007˙ Dynamic Workﬂow Change in PDM Systems, Computers in

Industry, 58, (5): 453–463.

10. Reisig, W., 1985. Petri Nets: An Introduction, Vol. 4 of EATCS Monographs on Theoretical

Computer Science, Springer.

11. Sibertin-Blanc, C., 2001. The Hurried Philosophers, in G. Agha, F. De Cindio, G. Rozenberg

(eds), Concurrent Object-Oriented Programming and Petri Nets, Advances in Petri Nets,

LNCS 2001, Springer, pp. 536–538.

12. van der Aalst, W. M. P., Basten, T., 2002. Inheritance of Workﬂows: An Approach to Tackling

Problems Related to Change, Theoretical Computer Science, 270,(1-2): 125–203.