The Elaboration and Clinical Testing of a New

Technique of Image Quality Improvement in Ultrasound

Medical Diagnostics

N. S. Kulberg

, T. V. Yakovleva

, Yu. R. Kamalov

, V. A. Sandrikov

L. V. Osipov

, P. A. Belov

Dorodnicyn Computing Centre of the Russian Academy of Science

Vavilova st., 40, Moscow 119333, RF

National Research Centre of Surgery

Abrikosovsky per. 2, Moscow 119992, RF

Izomed, ltd

Timiryazevskaya st. 1 corp. 2 Moscow 127422, RF

Abstract. The subject of the present research is solving the problem of the noi-

sy and the informative texture elements separation with taking into account the

specific traits of the ultrasound visualization. A noise suppression procedure is

realized on the basis of the elaborated mathematical model. The elaborated

technique has been tested in a clinic. The testing has confirmed its efficiency.

The work has been implemented under the support of the Russian Foundation

of Basic Research (RFBR), project № 08-01-12011-ofi.

1. Introduction

The main purpose of the investigations in the ultrasound medical visualization con-

sists in getting the most comprehensive information about the structure of the scatter-

ing biological tissue on the basis of scattered signal data analysis, and in further loca-

lization and characterization of the lesions. This task is far from its final solution. In

this field various particular applied tasks appear, such as the resolution improvement,

noise influence decrease, etc. Their main point is to insure the capability of the physi-

cian to identify the pathological changes on the background of the secondary image

elements that appear during the ultrasound image formation due to the influence of

various physical factors. The presence of the speckle structure is well known factor in

the visualization tasks. The speckle noise inevitably appears in the coherent imaging

systems. It is caused by the signals’ interference at scattering by the randomly distri-

buted very small objects. The speckle structure is imposed upon the useful texture of

the image. This kind of distortions is one of the most difficult for processing.

In the present work the speckle elements origination mechanism has been ana-

lyzed. The mathematical model has been developed to describe the basic elements of

the speckle structure according to the criteria of clinical usefulness and in correlation

with their spectral properties. Image improvement algorithm based upon the proposed

model has been developed and tested.

Kulberg N., Yakovleva T., Kamalov Y., Sandrikov V., Osipov L. and Belov P. (2009).

The Elaboration and Clinical Testing of a New Technique of Image Quality Improvement in Ultrasound Medical Diagnostics.

In Proceedings of the 2nd International Workshop on Image Mining Theory and Applications, pages 63-72

DOI: 10.5220/0001962300630072

 SciTePress

2. Comparison with Similar Results

Traditionally the noise suppression in digital visualization is based upon a priori

information about the differences in spatial spectra of the noisy and the useful ele-

ments of an image [1]. Thus, for some classes of images (for example, in digital pho-

tography) one can introduce a hypothesis that the useful elements’ spectrum is shifted

to lower band in comparison with the noise spectrum. Images in this case can be im-

proved by low frequency filtering.

Such approach works well only if the useful and noisy elements’ spectra can be re-

liably separated (e.g., for the small-grained photos). Such a processing is not applica-

ble when these spectra can not be distinguished between each other. The coherent

images which are characterized by the relatively large-scale interference noise ele-

ments cannot be improved by this way: depending upon the filter adjustments either

the image remains significantly noised, or the unacceptable meaningful small details

loss takes place.

In proposed technique the described drawbacks of the traditional approaches are

absent: the sharpness of the boundaries and the small-scale useful elements of the

image are kept even at high degrees of noise suppression.

Some investigators undertake the attempts to find such numeral parameter which

variations could become an indication of the presence of some pathologies in tissues

[2]. These works deal more with the attempts to automate the diagnostics process

rather than with the image quality improvement.

The most close prototype of the proposed technique is the method GOPView, that

was developed in 1980-s by Swedish company ContextVision [3]. All the software

products based upon this method are characterized by a common approach at which

the image being processed is described by means of a set of vector “features”, the

vector direction characterizing the “class” of an object (for example, the direction of

the boundary between two areas), and the vector length characterizing the “certainty”

of a feature. The image processing by means of this method consists in finding the

fields of “features” and their further analysis.

In our approach there is no intermediate step with the finding and analysis of the

“features”: the initial image elements are analyzed and filtered directly .

3. A Medical Problem Statement

Before discussing the mathematical criteria of the recognition of “useful” and “noisy”

elements of an image it is necessary to present a verbal “intuitive” description of the

investigated objects in such a way as they are perceived by a physician. Taking into

account the medical aspects of the problem together with the formal-mathematical

ones allows to increase the chances that the obtained solution will be really useful for

medics.

At visual analysis of an image the physician pays attention to two informative le-

vels in the image. They differ by size of the visualized objects relatively to the so-

called “resolution spot” of the acoustical system. This term means the minimal image

element which is distinguishable by the observer. This size in lateral area is deter-

mined by the acoustical system frequency: the smaller the frequency is, the worse its

lateral resolution is, and, consequently, the wider the “resolution spot” is. Its longitu-

dinal size is determined by the duration of the irradiated pulse: the longer the pulse is,

the worse is the longitudinal resolution and bigger is the “resolution spot”. The easiest

way to estimate the size of the “resolution spot” of a certain acoustical system is to

observe bright point reflectors of the acoustical phantom.

The first informative level (mentioned above) is a large-scale structure of the ob-

ject under investigation. At this level one can estimate the boundaries of organs and

their mutual disposition, the focal lesions and the large vessels. The macrostructure is

determined by the objects which size is larger than the “resolution spot” of the acous-

tical system. Due to this fact the definition of the correspondence of the macro-objects

in the acoustical image to real anatomic objects and the estimation of these objects’

properties is implemented relatively easily (we do not discuss here the various arti-

facts that can make the task more difficult). At diagnostics process the “direct” fea-

tures are estimated: the organs’ deformation (local or diffuse increase or decrease, the

presence of the local outpouching or retraction) and the violation of their normal

topography, the smoothness and clearness of the contours of the focal lesions, the

uniformity of the diameter and the right run of vessels.

The second informative level is presented by the small-scale structure. Here we

mean the various texture filling of extensive and relatively homogeneous areas of an

image of the parenchymatous organs. The structure of the scattering medium in this

case is characterized by the presence of a lot of scattering objects whose characteristic

size is of the order of tenth and hundredth portions of a millimeter. These are the the

cells layers of various orientation, arterioles and venules, small ducts, fibrous and fat

interlayers. At disease the morphological structure of these objects is changed. This

may lead to the changes of their acoustical properties. The local variations of the

brightness caused, for example, by small vessels, single small stones, etc., can also be

attributed to the small-scale structure level.

Thus, the microstructure of an image is determined by the scattering objects which

are smaller than “the resolution spot” of the acoustical system. An acoustical image of

such objects in principle does not have any geometric likeness with the original object

whereas within a single “resolution spot” there are tens and hundreds inhomogeneities

which are added statistically. As we deal here with the coherent adding of the acous-

tical oscillations, an interference amplification or weakening of the scattered signal

take place, which are not directly caused by the real changes of the reflective charac-

teristics of micro-objects (speckle-noise).

Nevertheless the change of the micro-objects’ scattering properties at various de-

ceases leads (though not directly) to the change of the image features. That is why the

characteristics of the texture structure of the picture that is obtained from these micro-

objects (including the speckle-noise) can serve as an indirect source of the informa-

tion about the disease nature. The changes of the brightness (the signal intensity), the

texture homogeneity and the degree of the attenuation of ultrasound signal are esti-

mated.

So, the morphological features of the objects under the study at macro- and micro-

levels are principally different. This fact causes the difference in approaches to their

analyzing. Obviously this leads to choosing the different mathematical means for

these informative levels’ processing.

4. Separation of Macro- and Micro- Structures

A two-dimensional discrete function f

, obtained as a result of ultrasound transducer

scanning along one special coordinate

, is being processed. Depending upon a real

scanning coordinates system this coordinate may correspond both to polar angle (the

convex and the sector transducers) and to one of the Cartesian coordinates (the linear

transducers).

An image comes to processing in the coordinate system of scanning, i.e. before

passing the scan-converter. These data have already been passed the procedure of

quadrature detection and logarithmic compression of the dynamic range.

For convenience of the mathematical estimations let us transfer from discrete func-

tions to the function of continuous variable:

⇒ fx

, y

(

)

⇒ fx, y

(

)

. This is possi-

ble under Nyquist-Shannon sampling theorem for functions having the finite spec-

trum. It should be noticed that the latter condition, i.e. the limited spectra’s ranges, is

valid with some approximations. However its validity is believed to be sufficient for

the most part of practical cases.

In order to separate the small-scale and large-scale image structures let us use the

procedure similar to the known method of pyramidal coding. We shall represent an

initial image

fx, y

()

as a sum:

fx, y

()

= M

x, y

(

)

+ m

x, y

(

)

(1)

Here m

x, y

()

is a function of the small-scale structure including mainly the in-

formation about small details of the initial image.

The function of large-scale structure is the following:

x, y

(

)

= fx, y

(

)

∗ψ x, y

(

)

(2)

It contains the information about large details of an initial image and is calculated

by means of the low frequency filtering (LFF) of the initial image function

fx, y

()

Here ψ x, y

()

is a pulse characteristic of some LFF, a sign

∗

means convolution. Let

us denote the spatial spectrum of this filter as

ΨΩ

, Ω

(

)

As the simulation results have shown the type of the LFF is not critical. The only

critical condition is the velocity of the monotonous decrease of the filter amplitude-

frequency characteristic (AFC) behind the cut frequency, which must be not less than

10 dB per octave. The principle meaningful factor is the choice of the cut frequencies,

what directly depend on the specific traits of the acoustical image acquisition. Let us

consider this issue in more detail.

The most important parameter of the images under our study is the so-called local

correlation radius. The results of many theoretical and experimental investigations

have shown its value to be determined mainly by the ratio between the emitted sig-

nal’s wavelength, the ultrasound pulse duration and correlation characteristics of the

object under the study. For the homogeneous areas which are characterized only by

the presence of a texture, the correlation radius is the least one and is determined by

the sizes of the “resolution spot” of the acoustical transducer R

. The filter cut fre-

quency is determined by the following formula:

1 R

(3)

The two-dimensional filter ψ x, y

(

)

can be built as a superposition of one-

dimensional LFFs with the cut frequencies calculated by the formula (3).

It should be noticed that the requirement to the scale properties of the filters to be

used depending upon the correlation characteristics of an image makes it difficult to

apply the wavelet transform, at which the spectral filter characteristics are rather de-

pendent upon the scale of the discrete image.

To build an improved image

x, y

(

)

we shall use an auxiliary “reconstruction

function”

Rx, y

()

for macrostructure and rx, y

(

)

for microstructure:

x, y

()

= M

x, y

()

+ m

x, y

(

)

= Rx, y

(

)

x, y

(

)

+ rx, y

(

)

x, y

(

)

(4)

The key moment of the present work determining its scientific novelty are the me-

thods of functions

Rx, y

()

and rx, y

(

)

calculation. These functions represent the

numerical criteria of the “usefulness” of any image element. Determining the function

rx, y

()

is of particular importance for us as the analysis and the processing of the

macrostructure, according to the authors’ opinion, present a less complicated task than

the processing of the textured “homogeneous” areas.

5. The Macrostructure and the Microstructure Processing

The macrostructure processing is relatively simple to implement. The main objects of

interest in the images determined by the function

x, y

(

)

, are the large objects’

boundaries. That is why the processing and improvement of such images can be con-

sidered as a kind of automated “retouch”. These techniques are well known and wide-

ly used in various graphical applications. For example, the most simple and evident is

the usage of an un-sharp masking method with the threshold criteria [1]. The other

ways of processing are also possible and their elaboration is not a difficult task. That

is why we shall not consider them here in detail. Significantly more difficult and

interesting task is the microstructure processing.

In order to explain the essence of the technique of the small-scale structure

processing developed in the present work, let us describe its main components and

provide their mathematical grounding. We shall suppose that the signal is emitted as

the focused Gaussian beam and that the signal spectrum is also Gaussian. We shall

consider the correlation radiuses

for both coordinates to be the same (this condi-

tion is easy to implement by simple change of one of the coordinates).

The main elements of speckle-structure are the “interference maximum” and the

“interference zero” (Fig. 1). Besides, some components of the macrostructure persist

in a function m

x, y

()

: first of all, the brightness “jumps”, determining the sharpness

of the objects’ boundaries.

1st scatterer signal

2nd scatterer signal

Summary signal (linear scale)

Summary signal (log. scale)

Sharp boundary signal

Fig. 1. Basic elements of the small-scale structure represented by the function m

x, y

()

(the

cross-sections of the values of two-dimensional function are presented along

-axis). Two

antiphase scattering objects result in the oscillation signal having two interference maxima

(useful) and one interference zero (harmful)

The interference maximum can be presented approximately as a logarithm of an in-

itial Gaussian “resolution spot” with some limit of the special extension:

− y

()

− x

()

rect

(

)

rect

(

)

(5)

Having implemented the Fourier transform we obtain the spatial spectrum that de-

creases while the frequency grows with the velocity ∼ 1 Ω

sin Ω

−

cos Ω

⎛

⎝

⎜

⎞

⎠

⎟

⋅

sin Ω

−

cos Ω

⎛

⎝

⎜

⎞

⎠

⎟

(6)

Within the surroundings of the “interference zero” the image function’s behavior

is, as a rule, linear, before the calculation of its logarithm. After the logarithm calcula-

tion we get a function

ln x rect

(

)

⋅ ln y rect

(

)

, (7)

with the spectrum :

⎛

⎝

⎜

⎞

⎠

⎟

∗

sin Ω

⎛

⎝

⎜

⎞

⎠

⎟

(8)

At last, the extensive boundary of two objects that is oriented along y -axis, is de-

scribed in the function

x, y

()

by the following expression:

ϑ x

(

)

∗δx

(

)

−ψ x, y

(

)

(

)

, (9)

where ϑ x

()

is a Heaviside function. The spectrum of (9) is the following:

⋅δ Ω

()

⋅ 1 −Ψ Ω

, Ω

()

(

)

(10)

Having averaged the obtained characteristic for all the angles of the boundary

orientation we get the formula:

+Ω

⋅ 1 −Ψ Ω

, Ω

()

(

)

(11)

From (11) it follows that the function will have a local maximum near the filter cut

frequency

ΨΩ

, Ω

(

)

. The presence of this maximum can be easily proved taking

into account the above introduced condition concerning the function

ΨΩ

, Ω

()

decreasing velocity.

The usefulness of three described elements is estimated on the basis of the analysis

of the investigated data distribution. Traditionally the behavior of the local amplitude

of the speckle-noise (let us denote it as

v ) is described by means of the Rayleigh

distribution:

()

exp

−v

⎛

⎝

⎜

⎞

⎠

⎟

, v > 0

. (12)

However this distribution is not applicable for all the cases (e.g., see [4], p. 213).

As an evident case of “non-Rayleigh” reflective medium one can propose the model

of a medium consisting of a lot of the reflectors of the same amplitude

and random

phases, these reflectors being distanced by

. The amplitudes of signals that have

been received from such a medium obey to the so-called

-distribution:

()

π vv

− v

()

, v ∈ 0, v

()

(13)

This distribution has a U-shaped density function, while the reflectors’ amplitude

which is to be estimated by us, is the upper boundary of the distribution values.

The distributions (12) and (13) just represent two extreme cases of the interference

picture behavior, and in practice we have something average. It is important for us

that the value under the estimation always lies between the mathematical expectation

and the maximum of the real distribution. This fact leads us to the following practical-

ly important conclusion: the “

interference zeros” in the image should be believed

to be more “harmful” elements of a texture than the interference maxima.

The comparison of the objects’ spectral characteristics with the degree of their use-

fulness has shown that the most “harmful” object is characterized by slower decreas-

ing of its spatial spectrum, and the most “useful” one possesses the local spectral

maximum near the frequency

. For this reason we propose to suppress harmful

texture details and to amplify useful ones by means of a filter characterized by the

amplification of the spatial frequencies within the range from 0 up to

, and by

suppression of higher spatial frequencies:



mx, y

(

)

= m

x, y

(

)

∗ψ

x, y

(

)

(14)

The certain shape of the filter pulse characteristic ψ

x, y

(

)

is determined empiri-

cally based upon the subjective estimation of the acquired image quality. It depends

upon the specific conditions of the measurements.

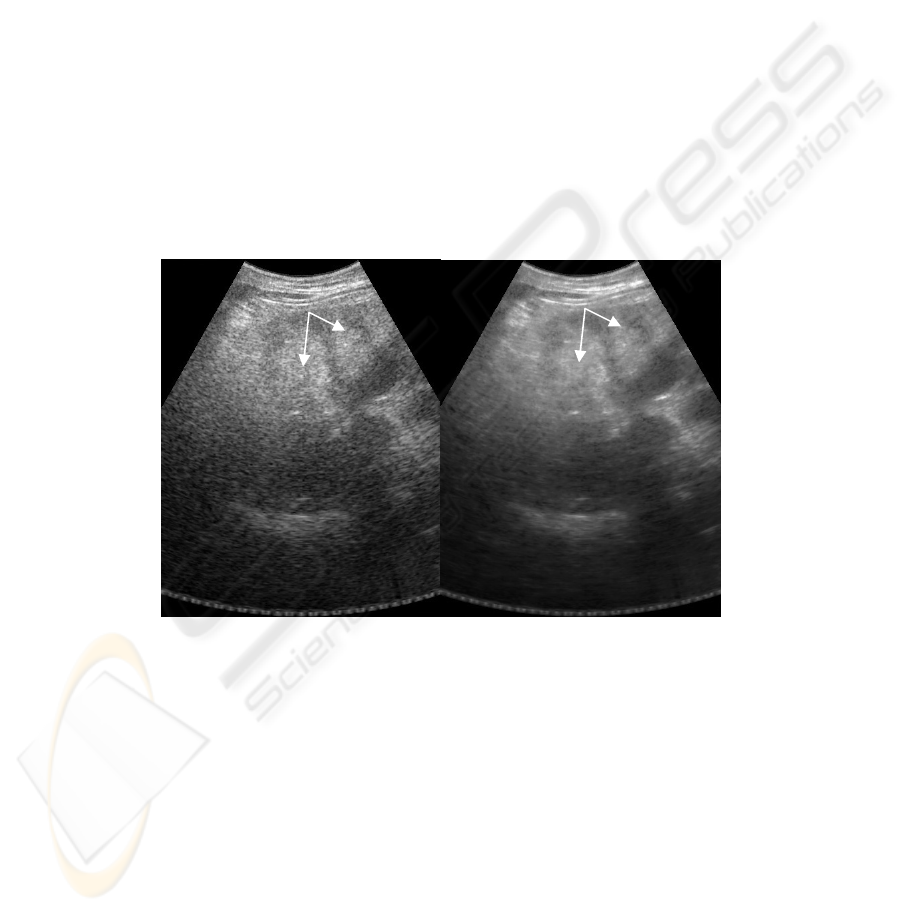
a) b)

Fig 2. An oblique scanning from under the right subcostal area: image of the gall-bladder

(marked by arrow) and right lobe of the liver. a) unprocessed image; b) processed image. After

the processing one can notice an improvement of the visualization of the walls of gall-bladder,

what makes it possible to get more reliable information about its shape. It is also possible to get

a more reliable estimation of the state of the internal gall-bladder’s contents

The main property of the function



mx, y

(

)

consists in the fact that its absolute

value in any point of the image increases with the degree of the usefulness of an

object situated in this point.

Consequently this function can be used as a function of

the microstructure reconstruction in formula (4). For additional tuning of the recon-

struction function properties one can introduce the nonlinear scaling of the small-scale

structure reconstruction function:

rx, y

()

=α

mx, y

()

(

)

(15)

where the

and

are parameters of the algorithm being available for the user

adjusting. By means of changing the parameters

and

one can achieve practically

a complete suppression of the small-scale texture areas of an image without loss of

large objects boundaries’ sharpness. The usage of the above described macro-objects

“retouch” procedure can still make them more clear. Thus processed picture approx-

imately resembles MR-image and can produce a good impression upon non-

specialists. Nevertheless, such excessive noise-suppression, according to the physi-

cians’ estimation, is not desirable and is even harmful.

6. Clinical Approbation

The techniques developed in the present work have been implemented as a soft-

ware package called RASP System

. This software was installed in the medical ultra-

sonic scanner A-4000 developed by Russian company Izomed, ltd. This scanner has

been approbated in the process of ultrasound examinations of patients in National

Research Centre of Surgery. Some results of clinical testing are included into the

present paper.

a) b)

Fig. 3. Scanning of the subcostal area from the right: image of the focal lesion in a liver (the

nodes of liver cells carcinoma are marked by arrows) on the background of the liver cirrhoses.

a) unprocessed image; b) processed image. The processing makes the contours of the liver

lesion more clear due to improving the visualization of the hypo-echoic area around it, and also

the visualization of the nearby situated hypo-echoic node on the background of the diffuse

changes of the liver parenchyma

During the tests we have compared the results of ultrasound visualization of some

organs of health people with the data obtained while examining the patients with

various diseases. These approbations have confirmed the efficiency of the proposed

techniques of the ultrasound image visual characteristics improvement, and, conse-

quently, a real possibility to increase the informative capacity and reliability of ultra-

sound medical diagnostics at the detected images processing. The results of this

processing are presented in Figs. 2—3.

At visual analysis of various abdominal objects images obtained in normal condi-

tion and in the cases of various diseases, by means of our program it has been found

out that:

1) The method makes it possible to make more certain conclusion about the shape

of the texture objects (liver, pancreas, spleen, kidneys), that provides the opportunity

of more confident their differentiation from the surrounding tissues and structures, to

get more reliable opinion about the smoothness or non-smoothness of these objects

boundaries and more precise definition of their sizes.

2) While using this processing one get the possibility of more assured revealing of

the focal lesions of the liver (both hyper-, and hypo-echoic) due to having more accu-

rate information about their boundaries, sizes and internal structure.

3) Clearer contouring of the liquid-containing objects (vessels, bile ducts, cysts) al-

lows more assured differentiation of these organs from the surrounding medium and

more reliable judgments about their anatomic construction.

4) The larger range of the contrast if compared with the standard imaging modes,

makes it possible to reveal more reliably the sludge (sand, small stones, etc.) in bile

ducts, and also to differentiate the liver ligaments.

7. Conclusion. The Perspectives of Further Investigation

The present paper is devoted to the processing of significantly “roughed” signals

that have passed the quadrature detection and the logarithmic compression of the

dynamic range. This results from the obvious fact: in most modern series devices it is

relatively easy the get an access to such a data. That is why, in spite of the obvious

insufficiency of these data their investigation and processing continue to be of a sig-

nificant interest. However according to the authors’ opinion the most perspective

direction in the ultrasound images improvement is the investigation and processing of

the radiofrequency “raw” data which are not practically used at the present time. Re-

ceiving the “raw” data in series devices will significantly extend the boundaries of the

ultrasound visualization due to the introduction of new techniques of the digital signal

processing.

References

1. R. Gonsalez and R. Woods, Digital Image Processing, second ed. Prentice Hall,

2001;

Wen-Chun Yen, Sheng-Wen Huang and Pai-Chi Li. Liver fibrosis classification

with B-mode ultrasound. Ultrasound in Med. & Biol., vol. 29, No 9, pp. 1229—

1235;

Official site of company ContextVision http://www.contextvision.com;

Physical Principles of Medical Ultrasonics. Edited by C. R. Hill, J. C. Bamber and

G. R. ter Haar. John Wiley & Sons, Ltd, 2003;