Data Improvement using Form Factors

Reconstructed in Latent Dimensions

Alexander Vinogradov

and Yury Laptin

Dorodnicyn Computing Centre of the Russian Academy of Sciences

Vavilov str. 40, 119333 Moscow, Russian Federation

Glushkov Institute of Cybernetics of the Ukrainian National Academy of Sciences

Academician Glushkov pr. 40, 03680 Kiev, Ukraine

Abstract. A new approach to the problem of enhanced description of cluster

boundaries in the sample is developed. New density estimates calculated on the

base of nonlinear reconstruction latent form factors in additional dimensions are

used for resolving critical loci in empirical distributions

1 Introduction

The idea to use form factors from accompanying dimensions, with a view of the im-

proved reconstruction of aprioristic density, is not new and is actively realized in the

ﬁeld of Image Processing and Image Mining. A typical example: aposteriori estima-

tions of an arrangement of the boundary points, depending on contextual conditions of

type of elasticity, entropy minimization, etc., used in functionals for Active Contours

and Balloons [1] [2] [3].

The reconstructed contour or spatial border of object can be considered as an exam-

ple of the substantial knowledgemined from the image. For a problem of tracing objects

in structure of scene or video sequence when the time interrelations are the subject to

be mined, adequate use of the contextual information is even more important. So, at

elimination scratches on the image, at segmentation of video sequence, at construction

of tools of type Time Machine for GIS [4], etc., aprioristic data on character of display

of the factor of time in data are used. The same is valid for use of other dominating

latent parameters proving in structure of the image. The choice both necessary types of

procedures and their parameters directly depends on the correct account of such data. In

an ideal, it is possible to look for systematization of aprioristic data, and for automatic

adjustment of data processing procedures on this base. Researches in this direction are

actual, ﬁrst of all, in the ﬁeld of Image Mining where the choice of a method directly

depends on type of the image [5] [7], but also in many other areas of data analysis [4]

[6]. In this paper a new approach to a problem of reconstruction of aprioristic density

is proposed in which improvement of the geometrical form of empirical distributions is

carried out on the basis of form factors determined by the relevant contextual informa-

tion.

Vinogradov A. and Laptin Y. (2009).

Data Improvement using Form Factors Reconstructed in Latent Dimensions.

In Proceedings of the 2nd International Workshop on Image Mining Theory and Applications, pages 93-99

DOI: 10.5220/0001963800930099

 SciTePress

2 Latent Dimensions

Methods of reconstruction and estimation of aprioristic distributionsare most demanded

in the problems related to research of cluster structures. As a rule, the incorrectness of

the problem of separation of clusters arises in view of the fact that attributes in used

space set a mediated data representation, and their numerical values in some combined

form reﬂect interrelation of various (stochastic and determined) factors deﬁning indi-

viduality of a class and localization of its representatives. From all variety of the state-

ments concerning to a problem of reconstruction of latent parameters, we address to a

situation when there is a uniformity of such mediation within the limits of a sample.

This assumption yields to investigate opportunities of the resolving critical variations

of empirical density on the basis of its reconstruction in latent dimensions. In case of

one additional dimension, on this way a problem arises that’s inverse to the problem

of estimation of integrated density on subspaces of co-dimension 1. For a direct prob-

lem there is the fast algorithm based on the use of geometrical properties of clusters of

representation [8]. In this work the speciﬁed inversion is formulated as a problem of a

choice of the optimal discrete K-layer scaling which corresponds to weakly changing

distributions of density in layers and itself satisﬁes to structural restrictions of type of

smoothness.

3 Hidden Exact Dependencies and Model of Data

In case of images the accompanying dimensions are present in initial representation

from the very beginning, but, in case of abstract feature spaces R

the comprehensible

kind of the latent parameters is not guaranteed in advance, and substantiations of a cor-

rectness of their reconstruction in additional coordinate subspace are necessary every

time. We shall be limited to a case when ontological assumptions specify an acceptabil-

ity of such treatment. In what follows, there is proposed a computational scheme where

these requirements are consolidated, and a method is developed for aprioristic density

estimation for that of involved in a solving rule in the form of projections on actual fea-

ture space some natural approximations of the distributions of classes reconstructed in

extended space with use of these structural restrictions. It is shown, that thus the various

difﬁculties related to overﬁtting and to adequate involvement of objects of type outliers

can be overcome. More strictly, we shall use the following model of data:

a) For the some n there are the strict analytical dependencies setting domain X in

space R

N +n

as admissible for representatives of a class.

b) These dependencies are smooth, and the geometrical form of immersing X ⊂

N +n

is simple.

c) Essential share of tangent spaces T

, x ∈ X, contains vectors from initial space

(i.e., in arrangement of sample there are local correlations between the latent and

observable dimensions).

d) Stochastic components bring their contribution to the mediated representation at

the stage of realization of the class in actual feature space R

e) Within the limits of area X stochastic components vary insigniﬁcantly.

Let’s explain in more detail the condition of item c). If there is more then one latent

parameter, metric parities between them are coordinated with scales of actual repre-

sentation, and degrees of their dependence on accessible dimensions can be compared

among themselves. Hence, every two smooth curves in R

N +n

are compatible on de-

gree of visibility in actual space (i.e., on the sum of nonzero local projections on R

that is, among them there is the best in this sense. We can not know both the value n

and nature of latent parameters, but, if some curve as their combination dominates over

others in the speciﬁed sense (’main hyper-surface’ of the sample, in a considered case

it’s ’main curve’), then it will be automatically reconstructed on the proposed way.

4 Clusters with Longitude

We shall search at ﬁrst stages of algorithm for some natural longitude of the cluster,

considering variations of empirical density as displays of non-linearity in X ⊂ R

N +n

which determine local relations between latent and actual coordinates.

4.1 Algorithm in Case of One Additional Dimension

1. Choose model of a layer (for example, unique Gaussian kernel) that describe local

features of realization of sample in R

, including both geometrical and stochastic com-

ponents. It is important to provide transformability of the density function p

on a layer

in R

in a density p

′

of a prototype of this layer L

′

in R

N +1

2. Build approximation of the whole empirical distribution in the form of convo-

lution of discrete set of points with the model of a layer (normal mixture with equal

weights and ﬁxed kernel is an example). Let F

be the functional of the quality of

approximation, C is a set of central points of the mixture C ⊗ L =

L(c

3. Build smooth ordering the centers of a mixture. It’s the central item of the method.

Let F

be a functional of quality of approximation of the discrete sequence of the centers

by some smooth curve S in R

. Let s

be the nearest to centers c

points on S.

Obligatory condition consists in that smooth should be either the evolution of distances

on S between new centers of consecutive layers. These restrictive condition gives an

opportunity of representation C in R

as a projection of some smooth uniform chain

′

merged in space R

N +1

4. Build prototype S

′

⊂ R

N +1

of the curve S ⊂ R

so that images s

′

∈ S

′

consecutive points from S settle down through the same intervals equal to the maximal

distance between consecutive centers in C. Corresponding fragments become horizon-

tal in R

N +1

(i.e., parallel to R

in immersion S

′

⊂ R

N +1

5. Fill extended space with models L

′

of the layer L transformed from dimension

to R

N +1

. The goal is to construct smooth tube S as an approximation of the proto-

type distribution in R

N +1

. The simplest way is to choose lot of equidistant points and

place transformed layers uniformly with corresponding small weights.

6. Projecting S back in R

, we receive improved estimation of the empirical den-

sity.

It is above presented the simple structure of algorithm which basic elements are

available in a ready form in MatLab environment. Furthermore, if back projections on

all transformed models of layers L

′

restore these layers without changes then items

4)-6) correspond simply to convolution of curve S with model of layer L of a kind

S ⊗ L =

We recall once again that in advance it is not known, which latent parameter will get

representation in additional dimension, but it will be one of the those better represented

in actual space, according to the assumption of item c).

So, on Fig. 1 a modelling example of an arrangement of clusters for two deeply

overlapped training classes describing two similar types of plants are represented.

Fig.1. An example of two deeply overlapped classes. Some representatives merged in alien media

seem to be outliers.

On Fig. 2 the result of modelling in additional dimension of the dominating latent

parameter is shown. At substantial interpretation it is visible, that representation re-

ceives the time scale which in this case is presented in the form of seasonal changes of

parameters of objects (color of leaves, and so on). Thus it is found out, that the main

distinction between classes consists in duration of the green period of vegetation of

these two types of plants while in all other respects they do not differ essentially from

each other.

On Fig. 3 it is shown, that adequate use of conditions of smoothness can lead to

separability of models of clusters reconstructed in extended feature space on the basis

of form factors. In particular, certain elements in an initial mix which from the point

of view of many criteria would be assigned to the category of outliers, in the extended

space take natural positions in own classes and bring therefore positive contribution to

the decision making.

5 Discussion

Introduction in structure of algorithm of more complex stages allows to involve the

important new opportunities. So, items 2 and 3 are closely interconnected, and for them

it is possible to construct joint functional of a kind F

= (F

, F

). This junction

determines a search of such approximation of cluster by a mix

L(x

), in which

the conﬁguration of the centers of layers provides their comprehensible ranking along

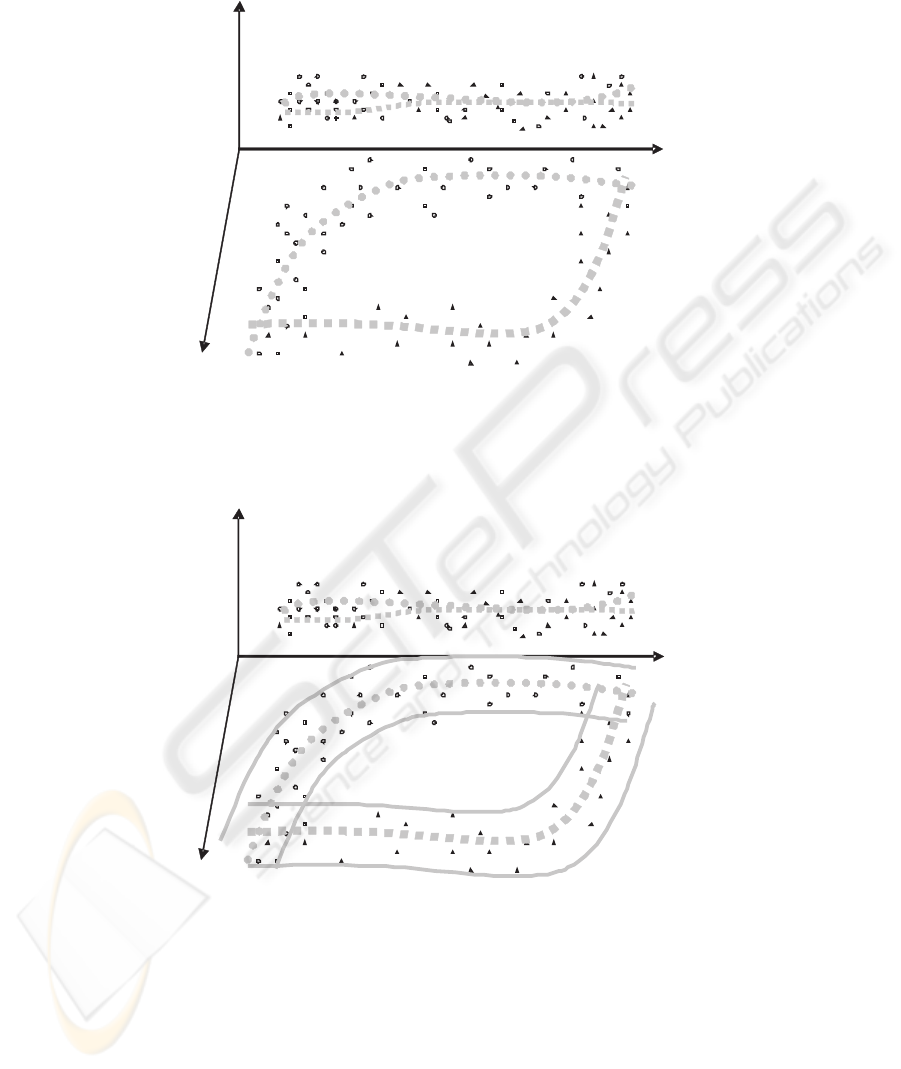
Fig.2. Modelling the dominating latent parameter in additional dimension. It becomes visible

that unique essential distinction between two classes of plants consists in duration of the green

period of vegetation. Equi-moment surfaces cross the lower plane from top-left to bottom-right.

Fig.3. Use of conditions of smoothness in the extended space. Some candidates to category of

outliers are rehabilitated and take natural positions in own classes.

a smooth curve, and either smooth evolution of distances between the adjacent centers.

In particular, for the sample originally represented by small symmetric kernels, this

problem can be put as a problem of a choice one-dimensional scaling in which the

model of a layer (item 1) serves as good approximation for all crossings of own layers

of the scaling with initial representation of the cluster. Thus, the constructed scale will

deﬁne the necessary ordering by itself.

Far more complicated variant assumes association of items 1, 2 and 3, i.e., simulta-

neous optimization of a choice as well the model of layer.

By introduction of the given complications it would be possible to build better ap-

proximations of the sample by ordered mix

L(x

), but even for F

the optimiza-

tion space can appear too complex and inaccessible for gradient methods. Inclusion

in analysis also a changing layer more aggravates the situation. One of possible ways

here can be the direct search and use of parallel calculations. Let {C} be the set of

initial conﬁgurations of the centers, {L} be the set of models of a layer. Product of their

counters can serve as rough lower estimate for the factor of parallelizing.

Certainly, domination any one of the latent parameters takes place not always and

even not often. Suitable approximation of the set of the centers C, for instance, on a

plane in the form of a discrete grid which could serve as a projection of the uniform

grid placed on a smooth surface in R

N +2

, in alternative cases can be more adequate.

But, the latter is considerably more challenging task, and a development of the method

at least for plane hardly will be immediate.

Therefore, the most natural niche for the method is its use in big systems for multi-

modal data analysis, where choice of procedures is coordinated with aprioristic infor-

mation. Systems of this type accumulate multiple partial decisions, the individual po-

tential of each of which can be limited, but the contribution in aggregated or collective

decision can become essential at association with other partial decisions.

Acknowledgements

This work was done in the framework of Joint project of the National Academy of

Sciences of Ukraine and the Russian Foundation for Basic Research No 08-01-90427

’Methods of automatic intellectual data analysis in tasks of recognition objects with

complex relations’.

References

1. Laurent D. Cohen: On active contour models and balloons. In: CVGIP: Image Understanding.

Volume 53, Issue 2 (1991) 211–218.

2. Yang Xiang, Albert C. S., Chung Jian Ye: An active contour model for image segmentation

based on elastic interaction. In: Journal of Computational Physics. Volume 219 Issue 1 (2006)

455–476.

3. Dimitris N. Metaxas, Ioannis A. Kakadiaris: Elastically Adaptive Deformable Models. In:

IEEE Transactions on Pattern Analysis and Machine Intelligence. Volume 24 Issue 10 (2002)

1310–1321.

4. Mikael Andersson, Bo Dahlin, Magnus Mossberg: Decision Support Systems for Forest Man-

agement. The Forest Time Machine - a multi-purpose forest management decision-support

system. In: Computers and Electronics in Agriculture. Volume 49 Issue 1 (2005) 114–128.

5. Joachim Gudmundsson, Marc van Kreveld, Giri Narasimhan: Region-restricted clustering for

geographic data mining. In: Computational Geometry. Volume 42 Issue 3 (2009) 231–240.

6. Yong Joon Lee, Jun Wook Lee, Duck Jin Chai, Bu Hyun Hwang, Keun Ho Ryu: Mining

temporal interval relational rules from temporal data. In: Journal of Systems and Software.

Volume 82 Issue 1 (2009) 155–167.

7. Colantonio S., Gurevich I. B., Salvetti O., Trusova Y.: An Image Mining Medical Warehouse.

In: Proceedings of International Workshop on Image Mining: Theory and Applications (IMTA

2008). I.Gurevich, H.Niemann, and O.Salvetti (eds.), INSTICC Press (2008) 83–92.

8. Alexander Vinogradov: Fast Multi-View Evaluation of Data Represented by Symmetric Clus-

ters. In: Proceedings of International Workshop on Image Mining: Theory and Applications

(IMTA 2008). I.Gurevich, H.Niemann, and O.Salvetti (eds.), INSTICC Press (2008) 53–57.