Adaptive Committees of Feature-specific Classifiers for
Image Classification
Tiziano Fagni, Fabrizio Falchi and Fabrizio Sebastiani
Istituto di Scienza e Tecnologia dell’Informazione
Consiglio Nazionale delle Ricerche
Via Giuseppe Moruzzi 1 – 56124 Pisa, Italy
Abstract. We present a system for image classification based on an adaptive
committee of five classifiers, each specialized on classifying images based on a
single MPEG-7 feature. We test four different ways to set up such a committee,
and obtain important accuracy improvements with respect to a baseline in which
a single classifier, working an all five features at the same time, is employed.
1 Introduction
An automated classification system is normally specified by specifying two essential
components. The first is a scheme for internally representing the data items that are the
objects of classification; this representation scheme, that is usually vectorial in nature,
must be such that a suitable notion of similarity (or closeness) between the representa-
tions of two data items can be defined. Here, “suitable” means that similar representa-
tions must be attributed to data items that are perceived to be similar. If so, a classifier
may identify, within the space of all the representations of the data items, a limited re-
gion of space where the objects belonging to a given class lie; here, the assumption of
course is that data items that belong to the same class are “similar”. The second com-
ponent is a learning device that takes as input the representations of training data items
and generates a classifier from them.
In this work we address single-label image classification, i.e., the problem of setting
up an automated system that classifies an image into exactly one from a predefined set
of classes. Image classification has a long history (see e.g., [1]), most of which has
produced systems that conform to the pattern described at the beginning of this section.
In this paper we take a detour from this tradition, and describe an image classifi-
cation system that makes use not of a single representation, but of five different ones
for the same data item; these representations are based on five different descriptors, or
“features”, from the MPEG-7 standard, each analyzing an image under a different point
of view. As a learning device we use a “committee” of five feature-specific classifiers,
i.e., an appropriately combined set of classifiers each based on the representation of the
image specific to a single MPEG-7 feature. The committees that we use are adaptive,
in the sense that, for each image to be classified, they dynamically decide which among
the five classifiers should be entrusted with the classification decision, or decide whose
decisions should be trusted more. We study experimentally four different techniques of
Fagni T., Falchi F. and Sebastiani F. (2009).
Adaptive Committees of Feature-specific Classifiers for Image Classification.
In Proceedings of the 2nd International Workshop on Image Mining Theory and Applications, pages 113-122
DOI: 10.5220/0001968501130122
Copyright
c
 SciTePress

combining the decisions of the five individual classifiers, using a dataset consisting of
photographs of stone slabs classified into different types of stone.
As a technique for generating the individual members of the classifier committee
we use distance-weighted k nearest neighbours, a well-known example-based learn-
ing technique. Technically, this method does not require a vectorial representation of
data items to be defined, since it simply requires that, given two data items, a distance
between them is defined. In the discussion that follows this will allow us to abstract
away from the details of the representation specified by the MPEG-7 standard, and sim-
ply specify our methods in terms of distance functions between data items. This is not
problematic, since distance functions both for the individual MPEG-7 features and for
the image as a whole have already been studied and defined in the literature.
Since distance computation is so fundamental to our methods, we have also studied
how to compute distances between data items efficiently, and have implemented an
efficient system that makes use of metric data structures explicitly devised for “nearest
neighbour search”.
The rest of the paper is organized as follows. Section 2 describes in detail the learn-
ing algorithm, while Section 3 discusses how we have implemented efficiently these
learning algorithms by recurring to metric data structures. In Section 4 we move to
describing our experiments, and to discuss conclusions that can be drawn from them.
2 Automatic Image Classification by means of Adaptive,
Feature-specific Committees
Given a set of documents D and a predefined set of classes (also known as labels, or
categories) C = {c
1
, . . . , c
m
}, single-label (aka 1-of-m, or multiclass) document clas-
sification (SLC) is the task of automatically building a single-label document classifier,
i.e., a function
ˆ
Φ that predicts, for any d
i
∈ D, the correct class c
j
∈ C to which d
i
belongs. More formally, the task is that of approximating, or estimating, an unknown
target function Φ : D → C, that describes how documents ought to be classified, by
means of a function
ˆ
Φ : D → C, called the classifier, such that Φ and
ˆ
Φ “coincide as
much as possible”
1
.
The solutions we will give to this task will be based on automatically generating
the classifiers
ˆ
Φ by supervised learning. This will require a set Ω of documents as
input which are manually labelled according to the classes C, i.e., such that for each
document d
i
∈ Ω the value of the function Φ(d
i
) is known. In the experiments we
present in Section 4 the set Ω will be partitioned into two subsets T r (the training set)
and T e (the test set), with T r ∪ T e = Ω; T r will be used in order to generate the
classifiers
ˆ
Φ by means of supervised learning methods, while T e will be used in order
to test the effectiveness (i.e., accuracy) of the generated classifiers.
1
Consistently with most mathematical literature we use the caret symbol (ˆ) to indicate estima-
tion.
114

2.1 Image Classifiers as Committees of Single-feature Classifiers
The image classifier
ˆ
Φ : D → C that we will generate will actually consist of a classi-
fier committee (aka classifier ensemble), i.e., of a tuple
ˆ
Φ = (
ˆ
Φ
1
, . . . ,
ˆ
Φ
n
) of classifiers,
where each classifier
ˆ
Φ
s
is specialized in analyzing the image from the point of view
of a single feature f
s
∈ F , where F is a set of image features. For instance, a classi-
fier
ˆ
Φ
colour
will be set up that classifies the image only according to its distribution of
colours, and a further classifier
ˆ
Φ
texture
will be set up that classifies the image accord-
ing to texture considerations. As image features we will use five visual “descriptors” as
defined in the MPEG-7 standard
2
, each of them characterizing a particular visual aspect
of the image. These five descriptors are Colour Layout (CL – information about the spa-
tial layout of colour images), Colour Structure (CS – information about colour content
and its spatial arrangement), Edge Histogram (EH – information about the spatial distri-
bution of five types of edges), Homogeneous Texture (HT – texture-related properties of
the image), and Scalable Colour (SC – a colour histogram in the HSV colour space)
3
.
The “aggregate” classifier
ˆ
Φ takes its classification decision by combining the de-
cisions returned by the feature-specific classifiers
ˆ
Φ
s
by means of an adaptive combi-
nation rule, i.e., a combination rule that pays particular attention to those
ˆ
Φ
s
’s that are
expected to perform more accurately on the particular image that needs to be classified.
This is advantageous, since different features could be the most revealing for classify-
ing different types of images; e.g., for correctly recognizing that an image belongs to
class c
′
the Homogeneous Texture feature might be more important than Colour Layout,
while the contrary might happen for class c
′′
. In the techniques that we have used in this
work, whether and how much a given feature is effective for classifying a given docu-
ment is automatically detected, and automatically brought to bear in the classification
decision.
For implementing the classifier committee, i.e., for combining appropriately the
outputs of the
ˆ
Φ
s
’s, we will experiment with four different techniques. In Sections 2.1
to 2.1 we will describe these techniques, while in Section 2.2 we will describe how to
generate the individual members of these committees.
Dynamic Classifier Selection. The first technique we test is dynamic classifier selec-
tion (DCS) [2–4]. This technique consists in
1. identifying the set
χ
w
(d
i
) = arg
w
min
d
p
∈T r
δ(d
i
, d
p
) (1)
of the w training examples closest to the test document d
i
, where δ(d
′
, d
′′
) is a
(global) measure of distance to be discussed more in detail in Section 3);
2. attributing to each feature-specific classifier
ˆ
Φ
s
a score g(
ˆ
Φ
s
, χ
w
(d
i
)) that measures
how well it classifies the examples in χ
w
(d
i
); see below for details;
2
International Organization for Standardization, Information technology - Multimedia content
description interfaces, Standard ISO/IEC 15938, 2002.
3
For definitions of these MPEG-7 visual descriptors see: International Organization for Stan-
dardization, Information technology - Multimedia content description interfaces - Part 3: Vi-
sual, Standard ISO/IEC 15938-3, 2002.
115

3. adopting the decision of the classifier with the highest score; i.e.,
ˆ
Φ(d
i
) =
ˆ
Φ
t
(d
i
)
where
ˆ
Φ
t
= arg max
ˆ
Φ
s
∈
ˆ
Φ
g(
ˆ
Φ
s
, χ
w
(d
i
)).
This technique is based on the intuition that similar documents are handled best by
similar techniques, and that we should thus trust the classifier which has proven to
behave best on documents similar to the one we need to classify.
We compute the score from Step (2) as
g(
ˆ
Φ
s
, d
i
) =
X
d
p
∈χ
w
(d
i
)
(1 − δ(d
i
, d
p
)) · [
ˆ
Φ
s
(d
p
) = Φ(d
p
)] (2)
where [α] is an indicator function, i.e.,
[α] =

+1 if α = T rue
−1 if α = F alse
Equation 2 thus encodes the intuition that the more examples in χ
w
(d
i
) are correctly
classified by
ˆ
Φ
s
(i.e., are such that
ˆ
Φ
s
(d
p
) = Φ(d
p
)), and the closer they are to d
i
(i.e,
the lower δ(d
i
, d
p
) is), the better
ˆ
Φ
s
may be expected to behave in classifying d
i
.
Weighted Majority Vote. The second technique we test is weighted majority vote
(WMV), a technique similar in spirit to the “adaptive classifier combination” technique
of [3]. WMV is different from DCS in that, while DCS eventually trusts a single feature-
specific classifier (namely, the one that has proven to behave best on documents similar
to the test document), thus completely disregarding the decisions of all the other clas-
sifiers, WMV uses a weighted majority vote of the decisions of all the feature-specific
classifiers
ˆ
Φ
s
∈
ˆ
Φ, with weights proportional to how well each
ˆ
Φ
s
has proven to be-
have on documents similar to the test document. This technique is thus identical to DCS
except that Step 3 is replaced by the following two steps:
3. for each class c
j
∈ C, all evidence in favour of the fact that c
j
is the correct class of
d
i
is gathered by summing the g(
ˆ
Φ
s
, χ
w
(d
i
)) scores of the classifiers that believe
this fact to be true; i.e.,
z(d
i
, c
j
) =
X
f
s
∈F :
ˆ
Φ
s
(d
i
)=c
j
g(
ˆ
Φ
s
, χ
w
(d
i
)) (3)
4. the class that obtains the maximum z(d
i
, c
j
) score is chosen, i.e.,
ˆ
Φ(d
i
) = arg max
c
j
∈C
z(d
i
, c
j
) (4)
Confidence-rated Dynamic Classifier Selection. The third technique we test is confi-
dence-rated dynamic classifier selection (CRDCS), a variant of DCS in which the confi-
dence with which a given classifier has classified a document is also taken into account.
From now on we will indeed assume that, given a test document d
i
, a given feature-
specific classifier
ˆ
Φ
s
returns both a class c
j
∈ C to which it believes d
i
to belong and a
116

numerical value ν(
ˆ
Φ
s
, d
i
) that represents the confidence that
ˆ
Φ
s
has in its decision (high
values of ν correspond to high confidence). In Section 2.2 we will see this to be true
of the feature-specific classifiers we generate in our experiment. Note also that, with
respect to the “standard” version of DCS described in Section 2.1, this “confidence-
aware” variant is more in line with the developments in computational learning theory
of the last 10 years, since confidence is closely related to the notion of “margin”, which
plays a key role in learning frameworks based on structural risk minimization, such as
kernel machines and boosting [5].
The intuition behind the use of these confidence values is that a classifier that has
made a correct decision with high confidence should be preferred to one which has
made the same correct decision but with a lower degree of confidence; and a classifier
that has taken a wrong decision with high confidence should be trusted even less than a
classifier that has taken the same wrong decision but with a lower confidence.
CRDCS is thus the same as DCS in Section 2.1, except for the computation of
the g(
ˆ
Φ
s
, d
i
) score in Step 2, which now becomes confidence-sensitive. In CRDCS
Equation (2) thus becomes
g(
ˆ
Φ
s
, d
i
) =
X
d
p
∈χ
w
(d
i
)
(1 − δ(d
i
, d
p
)) · [
ˆ
Φ
s
(d
p
) = Φ(d
p
)] · ν(
ˆ
Φ
s
, d
p
) (5)
Therefore,a classifier
ˆ
Φ
s
may be expected to perform accurately on an example d
i
when
many examples in χ
w
(d
i
) are correctly classified by
ˆ
Φ
s
, when these are close to d
i
, and
when these correct classifications have been reached with high confidence.
Steps 1 and 3 from Section 2.1 remain unchanged.
Confidence-rated Weighted Majority Vote. The fourth technique we test, confidence-
rated weighted majority vote (CRWMV), stands to WMV as CRDCS stands to DCS;
that is, it consists of a version of WMV in which confidence considerations, as from the
previous section, are taken into account. CRWMV has thus the same form of WMV; the
only difference is that the g(
ˆ
Φ
s
, d
i
) score as from Step 2 is obtained through Equation
(5), which takes into account the confidence with which the
ˆ
Φ
s
classifiers haveclassified
the training examples in χ
w
(d
i
), instead of Equation (2), which does not. Steps 1, 3 and
4 from Section 2.1 remain unchanged.
2.2 Generating the Individual Classifiers
Each individual classifier
ˆ
Φ
s
(i.e., each member of the various committees described in
Section 2.1) is generated by means of the well-known (single-label, distance-weighted)
k nearest neighbours (k-NN) technique. This technique consists in the following steps;
for a test document d
i
1. (similarly to Equation 1) identify the set
χ
k
(d
i
) = arg
k
min
d
p
∈T r
δ
s
(d
i
, d
p
) (6)
of the k training examples closest to the test document d
i
, where δ
s
(d
′
, d
′′
) is a
distance measure between documents in which only aspects specific to feature f
s
are taken into consideration, and k is an integer parameter;
117

2. for each class c
j
∈ C, gather the evidence q(d
i
, c
j
) in favour of c
j
by summing the
complements of the distances between d
i
and the documents in χ
k
(d
i
) that belong
to c
j
; i.e.,
q(d
i
, c
j
) =
X
d
p
∈χ
k
(d
i
) : Φ(d
p
)=c
j
(1 − δ
s
(d
i
, d
p
)) (7)
3. pick the class that maximizes this evidence, i.e.,
ˆ
Φ
s
(d
i
) = arg max
c
j
∈C
q(d
i
, c
j
) (8)
Standard forms of distance-weighted k-NN do not usually output a value of confidence
in their decision. We naturally make up for this by adding a further step to the process,
i.e.,
4. set the value of confidence in this decision to
ν(
ˆ
Φ
s
, d
i
) = q(d
i
,
ˆ
Φ
s
(d
i
)) −
P
c
j
6=
ˆ
Φ
s
(d
i
)
q(d
i
, c
j
)
m − 1
That is, the confidence in the decision taken is defined as the strength of evidence in
favour of the chosen class minus the average strength of evidence in favour of all the
remaining classes.
Distance-weighted k-NN classifiers have several advantages over classifiers gener-
ated by means of other learning methods:
– Very good effectiveness, as shown in several text classification experiments [6–
9]; this effectiveness is often due to their natural ability to deal with non-linearly
separable classes;
– The fact that they scale extremely well (better than SVMs) to very high numbers
of classes [9]. In fact, computing the |T r| distance scores and sorting them in de-
scending order (as from Step 1) needs to be performed only once, irrespectively of
the number m of classes involved; this means that distance-weighted k-NN scales
(wildly) sublinearly with the number of classes involved, while learning methods
that generate linear classifiers scale linearly, since none of the computation needed
for generating a single classifier
ˆ
Φ
′
can be reused for the generation of another
classifier
ˆ
Φ
′′
, even if the same training set T r is involved.
– The fact that they are parametric in the distance function they use. This allows the
use of distance measures customized to the specific type of data involved, which
turns out to be extremely useful in our case.
3 Efficient Implementation of Nearest Neighbour Search by
Metric Data Structures
In order to speed up the computations of our classifiers we have focused on imple-
menting efficiently nearest neighbour search, which can be defined as the operation of
finding, within a set of objects, the k objects closest to a given target object, given a
suitable notion of distance. The reason we have focused on speeding up this operation
is that
118

1. it accounts for most of the computation involved in classifying objects through the
k-NN method of Section 2.2; Step 1 of this method requires nearest neighbour
search;
2. it also accounts for most of the computation involved in combining base classi-
fiers through each of the four methods of Section 2.1; Step 1 of each of these four
methods also requires nearest neighbour search.
Efficient implementation of nearest neighbour search requires data structures in sec-
ondary storage that are explicitly devised for this task [10–12]. As such a data structure
we have used an M-tree [13]
4
, a data structure explicitly devised for speeding up near-
est neighbour search in metric spaces, i.e., sets in which a distance function is defined
between their members that is a metric
5
. We have been able to use M-trees exactly
because
– as the five feature-specific distance functions δ
s
of Equation 6, we have chosen the
distance measures recommended by the MPEG group (see [14] for details), which
are indeed metrics;
– as the global distance function δ of Equation 1 we have chosen a linear combination
of the previously mentioned five δ
s
functions, which is by definition also a metric.
As the linear combination weights w
s
we have simply adopted the weights derived
from the study presented in [15], i.e., w(CL) = .007, w(CS) = .261, w(EH) =
.348, w(HT ) = .043, w(SC) = .174.
Note that, in reality, the δ
s
functions from [14] that we have adopted do not range
on [0, 1], but on five different intervals [0, α
s
]; in order to have them all range on
[0, 1] we have multiplied all distances by the normalization weights z(CL) = .174,
z(CS) = .075, z(EH) = .059, z(HT ) = .020, z(SC) = .001.
4 Experiments
The dataset that we have used for our experiments (here called the Stone dataset) is
a set of 2,597 photographs of stone slabs, subdivided under 37 classes representing
different types of stone
6
. The dataset was randomly split into a training set, containing
approximately 30% of the entire dataset, and a test set, consisting of the remaining
70%. For each photograph an internal representation in terms of MPEG-7 features was
generated and stored into an M-tree.
4
We have used the publicly available Java implementation of M-trees developed at Masaryk
University, Brno; see http://lsd.fi.muni.cz/trac/mtree/.
5
A metric is a distance function δ on a set of objects X such that, for any x
1
, x
2
, x
3
∈ X, it is
true that (a) δ(x
1
, x
2
) ≥ 0 (non-negativity); (b) δ(x
1
, x
2
) = 0 if and only if x
1
= x
2
(iden-
tity of indiscernibles); (c) δ(x
1
, x
2
) = δ(x
2
, x
1
) (symmetry); (d) δ(x
1
, x
3
) ≤ δ(x
1
, x
2
) +
δ(x
2
, x
3
) (triangle inequality).
6
The dataset was provided by the Metro S.p.A. Marmi e Graniti company (see
http://www.metromarmi.it/),and was generated during their routine production pro-
cess, according to which slabs are first cut from stone blocks, and then photographed in order to
be listed in online catalogues that group together stone slabs produced by different companies.
119

As a measure of effectiveness we have used error rate (noted E), i.e., the percentage
of test documents that have been misplaced in a wrong class.
As a baseline, we have use a “multi-feature” version of the distance-weighted k-
NN technique of Section 2.2, i.e., one in which the distance function δ mentioned at
the end of Section 3, and resulting from a linear combination of the five feature-specific
δ
s
functions, is used in place of δ
s
in Equation 6. For completeness we also report five
other baselines, obtained in a way similar to the one above but using in each a feature-
specific distance function δ
s
. In these baselines and in the experiments involving our
adaptive classifiers the k parameter has been fixed to 30, since this value has proved
the best choice in previous experiments involving the same technique [7, 8]. The w
parameter of the four adaptive committees has been set to 5, which is the value that
had performed best on previous experiments we had run on a different dataset. In future
experiments we plan to optimize these parameters more carefully by cross-validation.
The results of our experiments are reported in Table 1. From this table we may
notice that all four committees (2nd row, 2nd to 5th cells) bring about a noteworthy
reduction of error rate with respect to the baseline (2nd row, 1st cell). The best performer
proves the confidence-rated dynamic classifier selection method of Section 2.1, with
a reduction in error rate of 39.7% with respect to the baseline. This is noteworthy,
since both this method and the baseline use the same information, and only combine
it in different ways. The results also show that confidence-rated methods (CRDCS and
CRWMV) are not uniformly superior to methods (DCS and WMV) which do not make
use of confidence values. They also show that dynamic classifier selection methods
(DCS and CRDCS) are definitely superior to weighted majority voting methods (WMV
and CRWMV).
This latter result might be explained by the fact that, out of five features, three (CS,
CL, SC) are based on colour, and are thus not completely independent from each other;
if, for a given test image, colour considerations are not relevant for picking the correct
class, it may be different to ignore them anyway, since they are brought to bear three
times in the linear combination. In this case, DCS and CRDCS are more capable of
ignoring colour considerations, since they will likely entrust either the EH- or the HT-
based classifier with taking the final classification decision.
The same result also seems to suggest that, for any image, there tends to be a single
feature that alone is able to determine the correct class of the image, but this feature is
not always the same, and sharply differs across categories. For instance, the SC feature
is the best performer, among the single-feature classifiers (1st row), on test images
belonging to class GIALLO VENEZIANO (E = .11), where it largely outperforms the
EH feature (E = .55), but the contrary happens for class ANTIQUE BROWN, where
EH (E = .01) largely outperforms SC (.22). That no single feature alone is a solution
for all situations is also witnessed by the fact that all single-feature classifiers (1st row)
are, across the entire dataset, largely outperformed by both the baseline classifier and
all the adaptive committees. This fact confirms that splitting the image representation
into independent feature-specific representations on which feature-specific classifiers
operate is a good idea.
120

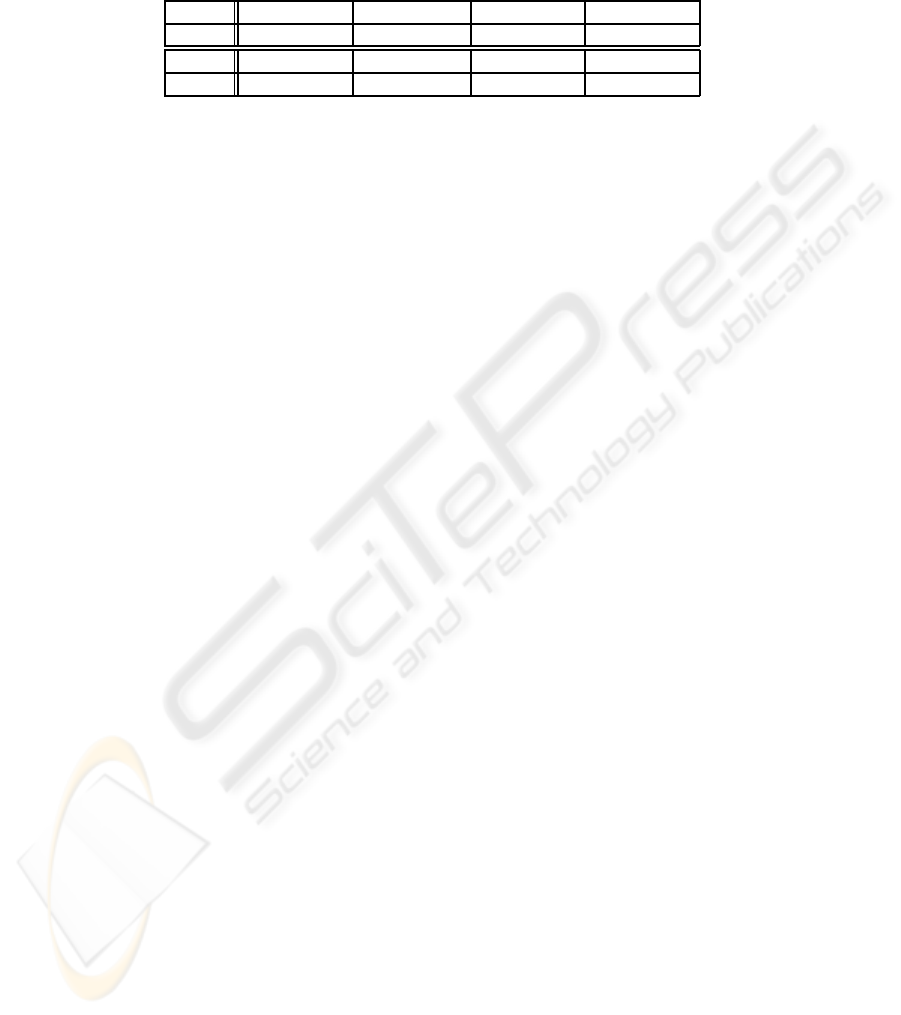
Table 1. Error rates of the techniques as tested on the Stone dataset; percentages indicate de-
crease in error rate with respect to the baseline. The first five results are relative to the five
feature-specific baselines. Boldface indicates the best performer.
CL CS EH HT SC
0.479 0.318 0.479 0.410 0.419
Baseline DCS CRDCS WMV CRWMV
0.297 0.183 (-38.4%) 0.179 (-39.7%) 0.225 (-24.2%) 0.227 (-23.6%)
Acknowledgements
This work has been partially supported by Project “Networked Peers for Business”
(NeP4B), funded by the Italian Ministry of University and Research (MIUR) under
the “Fondo per gli Investimenti della Ricerca di Base” (FIRB) funding scheme. We
thank Gianluca Fabrizi and Metro S.p.A. Marmi e Graniti for making the Stone dataset
available. Thanks also to Claudio Gennaro and Fausto Rabitti for useful discussions.
References
1. Lu, D., Weng, Q.: A survey of image classification methods and techniques for improving
classification performance. International Journal of Remote Sensing 28(5) (2007) 823-870
2. Giacinto, G., Roli, F.: Adaptive selection of image classifiers. In: Proceedings of the 9th
International Conference on Image Analysis and Processing (ICIAP’97), Firenze, IT (1997)
38-45
3. Li, Y.H., Jain, A.K.: Classification of text documents. The Computer Journal 41(8) (1998)
537-546
4. Woods, K., Kegelmeyer Jr, W., Bowyer, K.: Combination of multiple classifiers using local
accuracy estimates. IEEE Transactions on Pattern and Machine Intelligence 19(4) (1997)
405-410
5. Schapire, R.E., Singer, Y.: Improved boosting using confidence-rated predictions. Machine
Learning 37(3) (1999) 297-336
6. Joachims, T.: Text categorization with support vector machines: Learning with many rel-
evant features. In: Proceedings of the 10th European Conference on Machine Learning
(ECML’98), Chemnitz, DE (1998) 137-142
7. Yang, Y.: An evaluation of statistical approaches to text categorization. Information Retrieval
1(1/2) (1999) 69-90
8. Yang, Y., Liu, X.: A re-examination of text categorization methods. In: Proceedings of the
22nd ACM International Conference on Research and Development in Information Retrieval
(SIGIR’99), Berkeley, US (1999) 42-49
9. Yang, Y., Zhang, J., Kisiel, B.: A scalability analysis of classifiers in text categorization. In:
Proceedings of the 26th ACM International Conference on Research and Development in
Information Retrieval (SIGIR’03), Toronto, CA (2003) 96-103
10. Ch·vez, E., Navarro, G., Baeza-Yates, R., Marroqu
`
In, J.L.: Searching in metric spaces. ACM
Computing Surveys 33(3) (2001) 273-321
11. Samet, H.: Foundations of Multidimensional and Metric Data Structures. Morgan Kaufmann,
San Francisco, US (2006)
121

12. Zezula, P.,Amato, G., Dohnal, V., Batko, M.: Similarity Search: The Metric Space Approach.
Springer Verlag, Heidelberg, DE (2006)
13. Ciaccia, P., Patella, M., Zezula, P.: M-tree: An efficient access method for similarity search
in metric spaces. In: Proceedings of the 23rd International Conference on Very Large Data
Bases (VLDB ’97), Athens, GR (1997) 426-435
14. Manjunath, B., Salembier, P., Sikora, T., eds.: Introduction to MPEG-7: Multimedia Content
Description Interface. John Wiley & Sons, New York, US (2002)
15. Amato, G., Falchi, F., Gennaro, C., Rabitti, F., Savino, P., Stanchev, P.: Improving image
similarity search effectiveness in a multimedia content management system. In: Proceedings
of the 10th International Workshop on Multimedia Information System (MIS’04), College
Park, US (2004) 139-146
122