
MATHPORT
Web Application to Support Enhancement in Elementary Mathematics Pedagogy
Barbara Koroušić Seljak, Gregor Papa
Computer Systems Department, Jožef Stefan Institute, Jamova c. 39, Ljubljana, Slovenia
Barbara Japelj Pavešić
Educational Research Institute, Gerbičeva 62, Ljubljana, Slovenia
Keywords: Web application, Open-source software, Genetic algorithm, Elementary school mathematics, Pedagogy
enhancement.
Abstract: The paper presents a Web application MatPort that is aimed to support enhancement in elementary
mathematics pedagogy. In Slovenia, there is a lack of e-Learning courses on elementary school mathematics
that would provide teachers and students with verified mathematics problems in Slovene language. The
MatPort offers a databank of verified mathematics problems that may be solved on paper or at a computer,
or combined into a paper and pencil form of tests. In this paper, we describe the structure and the
functionality of the application, providing an insight into the MatPort decision system that supports
automatic search of math problems so that students may reach a certain level of knowledge in a thoughtful
way. The decision support system is based upon the genetic algorithm. The application has been evaluated
by a group of teachers and students, who have been actively involved into the MatPort development.
1 INTRODUCTION
One of modern ways of education delivery is e-
Learning, which is a broad term used to describe
learning done at a computer, usually connected to
the World Wide Web. It is widely accepted that e-
Learning can be as rich and as valuable as the
classroom experience or even more so. With its
unique features e-Learning is an experience that
leads to comprehension and mastery of new skills
and knowledge, just like its traditional counterpart.
Instructional design for e-Learning, which is the
systematic process of translating general principles
of learning and instruction into plans for
instructional materials and learning, has been
perfected and refined over many years using
established teaching methods, with many benefits to
students.
1.1 Learning Styles
There are three predominant learning styles
(Donovan, 2000):
Visual;
Auditory;
Tactile/kinesthetic.
Broken down further, people learn by reading and
seeing (visual style), listening and speaking
(auditory style) and doing (tactile/kinesthetic style).
Reading, listening and seeing are passive types of
learning, while speaking and doing are active types
of learning. How much we tend to remember is a
function of the type of learning we prefer and our
level of involvement in the learning. People often
learn through a combination of the ways described
above. To a lesser degree, environment is a factor
too.
Given a good learning environment, most people
tend to understand and remember (i.e., learn) best
when practicing the real thing. Being actively
engaged in hard and challenging activities strongly
supports them to construct knowledge for
themselves. Next, a combination of observing
people we respect, doing and speaking about what
we learn produces a high retention rate, followed by
speaking alone.
In e-Learning, it is important to provide a variety
of activities supported by human intervention. A lot
81
Korouši
´
c Seljak B., Papa G. and Japelj Paveši
´
c B. (2009).
MATHPORT - Web Application to Support Enhancement in Elementary Mathematics Pedagogy .
In Proceedings of the First International Conference on Computer Supported Education, pages 81-88
DOI: 10.5220/0001974000810088
Copyright
c
SciTePress
of passive learning may be done through reading
text, listening to audio clips, and seeing graphics,
while the active mode should be stimulated through
practising, e.g., solving mathemathics problems.
1.2 Unique e-Learning Features
There are several unique features of e-Learning:
e-Learning is self-paced and gives students a
chance to speed up or slow down as
necessary;
e-Learning is self-directed, allowing students to
choose content and tools appropriate to their
differing interests, needs, and skill levels;
Designed around the learner;
Geographical barriers are eliminated, opening
up broader education options;
Enhances computer and internet skills.
1.3 Mathematics e-Learning Support
in Slovenia
Učiteljska.net (http://uciteljska.net/) and e-um
(http://www.e-um.si/) are good examples of Slovene
Web applications aimed to support e-Learning of
elementary school mathematics. While the first one
is intended to support exchange of teacher
experience and information, the second one provides
interactive online courses for students.
However, there is a lack of online courses in
Slovene language on solving verified mathematics
problems for children under 15 years of age. For this
reason, we have developed a new Web application
for e-Learning of elementary school mathematics in
an active learning mode, called MatPort
(http://sinica.ijs.si/matport/).
The rest of the paper is organized as follows:
Section 2 describes the content and the technology
aspects of the Web application. Section 3 outlines
the concept of the decision support system that may
be used as an automatic search facility. The
experimental work is presented in Section 4.
Conclusions and directions for further work are
given in Section 5.
2 WEB APPLICATION MATPORT
The Web application MatPort is based upon the
national curriculum for elementary school
mathematics and upon verified mathematical
problems.
2.1 Web Content Aspect
For the pilot stage of the project, we decided to use a
collection of verified sets of mathematics problems
in Slovene language, published in the form of flash
cards, which have been used for many years in our
schools. These problem solving items already passed
through many steps of evaluation, therefore, they are
valuable. Some of the real life items needed to be
updated for the present time. By this stage, we have
focused on the grades 6 to 9 or the age group 12 to
15 years old students.
With the help of experienced teachers we
classified the items into subgroups with respect to
the knowledge required for problem solving by
content and three difficulty levels.
Finally, we designed and developed the MatPort
Web application with the following modules for:
1. Entering math items, their solutions and
teaching instructions into a database for
teachers and administrators;
2. Solving math items;
3. Preparing a paper and pencil form of test;
4. Providing other information relevant for
teaching the elementary school mathematics.
The first and the third module are aimed for
teachers, the second one for students and the last one
for teachers and parents.
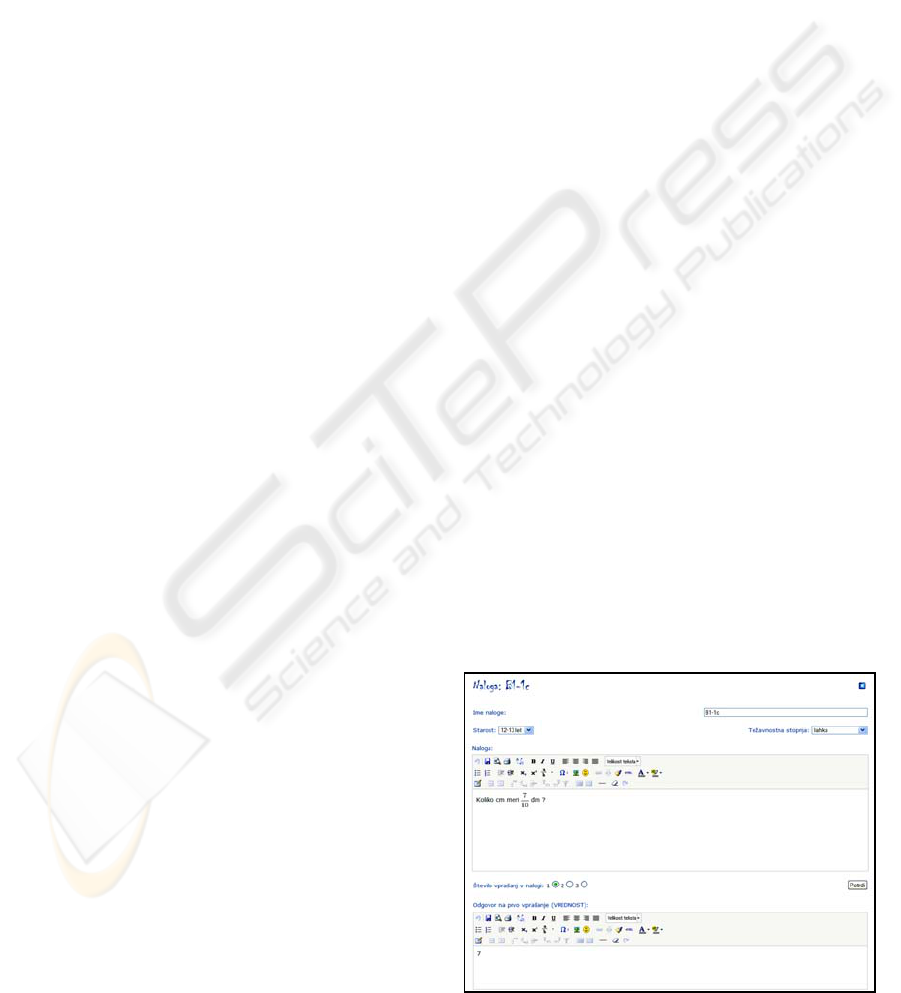
2.1.1 Entering Math Items
A user registered as a teacher may enter his/her
items into the MatPort database (Fig. 1). Each item
is described with a problem definition, solution(s) in
terms of values and units, content area, difficulty
level, source or author, and teaching instructions.
The user may copy an already validated math item
and adapt it to its needs.
Figure 1: Entering Math Items.
CSEDU 2009 - International Conference on Computer Supported Education
82

The math items saved in the database are
accessible only to the user. However, (s)he can
outbid any of his/her items to other MatPort users.
Before publishing this item as a public one, experts
verify it and suggest modifications if required.
Teachers are informed of their activities through
a simple statistics on math items collected in the
MatPort database.
2.1.2 Solving Math Items
A user registered as a teacher or a student may solve
any public or his/her own math item from the
MatPort databank. The application provides manual
and automatic search of math items in content areas
defined by the national curriculum for elementary
school mathematics. The automatic search is
provided by a decision support system that is
described in detail in Section 3.
Ones an item is selected, the user can print it and
solve the problem in a classical paper and pencil
way, or directly provide solution(s) to the MatPort.
The application evaluates the answer(s) and denotes
the item as correctly or incorrectly solved problem
by this user.
Users are given information on the progress in
solving math items through graphycal symbols and
stimulative words (Fig. 2). More specifically, if the
user correctly solves more than 45%, 60%, 75% or
90% of dealt items, respectively, (s)he is rewarded
with one, two, three, four or five stars, respectively.
Figure 2: Solving Math Items – information.
If required, users may get teaching instructions
for math items (Fig. 3). They can also use a forum
integrated into the application to communicate with
other users or experts.
2.1.3 Preparing Tests
The MatPort supports design of paper and pencil
form tests to examine the students’ knowledge in a
classroom. A user may select a set of items, modify
them if needed, define the test’s header and print the
test. The application also offers a printout of
solutions to the selected math items.
Figure 3: Solving Math Items - teaching instructions.
2.1.4 Providing Information
We support teachers and parents with information on
elementary school mathematics, such as (Fig. 4):
Results on the IEA (International Association
for the Evaluation of Educational
Achievement) TIMSS Advanced Assessment
Frameworks, which – carried out every four
years at the fourth and eighth grades provides
data about trends in mathematics and science
achievement over time;
The national curriculum for elementary school
mathematics;
Practical advices to parents on helping students
learning mathematics at home;
Education debate on motivation methods and
tools for engaging students in the process of
active learning mathematics.
Figure 4: MatPort web application.
2.2 Web Technology Aspect
The MatPort was designed and developed using
state-of-the-art technologies. We applied a UML
(Unified Modelling Language) based model-driven
MATHPORT - Web Application to Support Enhancement in Elementary Mathematics Pedagogy
83

methodology (http://www.uml.org/) to cover the
life-cycle of the Web application development.
2.2.1 Design
To design the application sympathetically with the
way students, teachers and parents actually use the
Web, not how we think they should, we directly
involved experienced teachers into the project.
The MatPort database was designed as a
rational database, consisting of tables that store data
on:
User profiles;
Math items;
Knowledge required for solving items;
Relations between the content areas;
History of items’ solving.
The database structure is given in Fig. 5.
Figure 5: Rough draft of the MatPort database structure.
The application consists of several dynamic and
static modules, such as:
Module for providing math items;
Math item solver module;
Test generator module;
Informer module;
Forum;
Download center.
The informer module has a static content that is
managed by a content management system, while
the others may change their content in a dynamic
way. The Web application structure is shown in Fig.
6.
2.2.2 Development
As the project’s budget was low and we needed to
minimize the cost, we decided to make good use of
open-source and freely available software. We
applied:
Figure 6: Rough draft of the MatPort use case.
Apache (http://www.apache.org/) as a Web
server that replies to Web clients’ requests via
HTTP (HyperText Transfer Protocol);
MySQL (http://www.mysql.com/) as a
database management system that is based
on the relational model;
PHP5 (HyperText Preprocessor)
(http://www.php.net/) as a server-side
technology. This is also a scripting language
that has evolved to include a command line
interface capability and can be used in
standalone graphical applications. PHP5 offers
standardized means for specifying the variety
of property scopes typically offered by object-
oriented languages (Hayder, 2007);
JavaScript (Darie et al, 2006) as a client-side
technology. This is another scripting
language, whose code is written in plain text
and can be embedded into HTML (HyperText
Markup Language) pages to empower them.
The MatPort is aimed for doing mathematics,
which means that mathematical symbols need to be
supported. For this reason, we integrated TinyMCE
(http://tinymce.moxiecode.com/) as a platform
independent JavaScript WYSIWYG editor. It has
the ability to convert HTML TEXTAREA fields or
other HTML elements to editor instances. Because
CSEDU 2009 - International Conference on Computer Supported Education
84

TinyMCE supports only standard HTML math
symbols, we extended its library with a module for
handling mathematical expressions. Once entered,
these are rendered into images using the
LatexRender scripts
(http://www.mayer.dial.pipex.com/tex.htm).
All MatPort printouts have the standard PDF
(Portable Document Format) format.
The MatPort forum is based upon the PHPBB
TM
(http://www.phpbb.com/) open-source forum
solution.
Last but not least, we set formatting MatPort
visual options in a centralized document that is
referenced from PHP files by using CSS (Cascading
Style Sheets).
3 DECISION SUPPORT SYSTEM
We are aware of the fact that only providing a
dataset of math items is not enough. We need to
incorporate an extrinsic motivation system to
“bribe” the 6
th
to 9
th
grade students to practice
mathematics. There are rare children who are
intrinsically motivated to do repetitive, boring tasks.
3.1 How to Motivate Children?
A student who solves a MatPort math item receives
information on the progress through graphical
symbols and stimulative words (Fig. 2).
In addition, the application provides information
on math items that need to be further solved to
receive a higher score. These can be supplementary
or additional items to help strengthen or increase
knowledge, respectively. The information is
provided by the MatPort decision support system,
when the automatic search facility is used.
3.2 Genetic Algorithm
The MatPort decision support system that motivates
students to continue solving exercises is based upon
an evolutionary computation method, i.e., the
genetic algorithm (GA) (Goldberg, 1989; Bäck,
1996).
The GA is based on a heuristic method, which
requires little information to search effectively in a
large search space. The algorithm employs an initial
population of chromosomes, which evolve to the
next generation by probabilistic transition rules
(randomized genetic operators) such as selection,
crossover and mutation. The objective function
evaluates the quality (fitness) of solutions coded as
chromosomes. This information is used to perform
an effective search for better solutions. There is no
need of other auxiliary knowledge. The GA tends to
take advantage of the fittest solutions by giving them
greater weight and by concentrating the search in the
regions of the search space with likely improvement.
The GA mechanism is presented in Fig. 7.
Initialize the population of
chromosomes;
While stop condition not met do:
Calculate the fitness for each
member in the population using the
fitness function
;
Select and reproduce individuals
according to their fitness;
Perform genetic operators
(crossover and mutation) on the
population.
Figure 7: The GA’s pseudocode.
The GA is a population-based evolutionary
approach that allows searching within a broad set of
solutions from the search space simultaneously.
Namely, because there are many math items (few
hundreds or even more than thousand math items per
a grade) and interrelated content areas (more than
100 content areas per a grade), the student may
continue solving items in many possible ways that
may or may not lead to a higher score. Moreover,
math items are dynamically generated by teachers
(i.e., the item dataset expands with time) and the
student may start solving them anywhere in the
dataset. In the GA, there is a risk of converging to a
local optimum, but good results of various research
work obtained in other optimization problem areas
(Papa and Koroušić Seljak, 2005; Koroušić Seljak,
2006; Tušar et al, 2007; Korošec and Šilc, 2008)
encouraged us to consider the GA approach as a
promising approach to the decision making problem.
The idea is to find a set of math items within
different content areas that, when solved
correctly, improve the user’s knowledge and
increase his/her score as much as possible. The set
of items should consist of math problems from all
poorly scored content areas and the areas that
precede these areas. Therefore, before start
searching, the system identifies all the feasible
items, i.e., math problems from the poorly scored
content areas. These items form some kind of a pool
of relevant items P for current score improvement.
3.2.1 Encoding
The suggested list of math items needed to improve
the score is encoded into a chromosome, where each
MATHPORT - Web Application to Support Enhancement in Elementary Mathematics Pedagogy
85

gene represents the identification (ID) number of the
item in the MatPort database. The chromosome
length has been fixed to 15, while this number
represents a reasonable number of items to perform,
in order to significantly improve the score. Fig. 8
presents the chromosome with such number of genes
and the IDs of the items to be performed in the order
as encoded in the chromosome.
1 2 3 4 5 14
15
45 124 33 79 186 … 247
31
Figure 8: Chromosome of length 15 that represents a set of
items to be solved to increase the current score.
3.2.2 Population Initialization
The initial population consists of n chromosomes.
Each chromosome is initialized with randomly
chosen items from the pool of relevant math items.
3.2.3 Genetic Operators
In the selection process, the elitism strategy is
applied through the substitution of the least-fit
chromosomes with the equal number of the best-
ranked chromosomes.
With the one-point crossover scheme,
chromosome mates are chosen randomly and with a
probability p
c
all values after randomly chosen
position are swapped, which leads to two new
solutions that replace their original sources. Fig. 9
shows a crossover example.
45 124 33 79 186 … 247
31
12 14 233 56 228 … 269
41
⇓
⇓
45 124 33 56 228 … 269
41
12 14 233 79 186 … 247
31
Figure 9: One-point crossover.
In the mutation process each value of the
chromosome mutates with a probability p
m
. If the
value of the chromosome needs to be changed, than
some new value from the pool of relevant math
items is chosen. However, since a high mutation rate
resulted in a random walk through the GA search
space, p
m
has to be chosen to be somewhat low. Fig.
10 shows a mutation example.
45
124
33
79
186 … 247 31
⇓
⇓
45
137
33
56
12 … 269 41
Figure 10: Mutation.
3.2.4 Fitness Evaluation
After the recombination operators modify the
solutions, the whole new population of
chromosomes is ready to be evaluated. In the
evaluation process the set of math items is assumed
to be solved correctly and the score improvement is
calculated. The calculated score improvement is
used as a fitness value of each chromosome. Here all
the items are weighted with their difficulty grade;
the order of items is relevant when the problems
belong to different content areas that derive from
each other.
3.2.5 Parameter Settings
In order to ensure optimal solutions in a reasonable
response time robust parameter settings need to be
found for the population size, number of
generations, selection criteria and genetic operator
probabilities:
If the population size and the number of
generations are too small, the GA converges
too quickly to a local optimal solution and
may not find the best solution. On the other
hand, a large population and too much
iteration require long time to converge to a
region of the search space with significant
improvement. In our case, we have used the
population size n=15 and number of
generations n
g
=30;
Applying the elitism strategy, fitter solutions
have greater chance to be reproduced. But
when the number of worse solutions to be
exchanged with better ones (the selection
criteria) is too high, the GA is trapped too
quickly in a local optimum solution. Our
selection rate has been 20%;
Too low crossover probability preserves
solutions to be interchanged and longer time is
required to converge. This probability should
be large enough to crossover almost all mated
solutions. In our case, efficient setting for p
c
has been 70%;
Too high mutation probability may introduce
too much diversity and takes longer time to
reach an optimal solution. Too low mutation
CSEDU 2009 - International Conference on Computer Supported Education
86

probability tends to miss some near-optimal
solutions. Again, the efficient setting for p
m
has been 5%.
3.2.6 Termination
When a certain number of populations are generated
and evaluated, the system is assumed to be in a non-
converging state. A chromosome with the highest
score improvement is chosen as a final result.
On average, the GA finds an optimal selection of
math items that need to be further solved by the user
to receive a higher score in order of few seconds. As
it is implemented as a background process, it does
not slow down the application.
4 EXPERIMENTAL WORK
During the current pilot stage of the MatPort
application, we have involved a group of elementary
school teachers and a group of the 8
th
grade students
to test the application facilities.
We have examined the MatPort effectiveness for
delivery of elementary mathematics e-Learning. In
the group of teachers, we have been interested in:
1. The number of new math items provided by
the teachers;
2. The number of copied and modified already
validated math items;
3. The number of written tests designed by the
MatPort.
In the group of students, we have been interested
in:
1. The time spent in each content area;
2. The number of correctly and incorrectly
solved exercises in each knowledge field;
3. The correlation between the MatPort scores
and school marks before and after the period
of testing the MatPort;
4. Frequency of using the MatPort automatic
search (decision support system) facility.
Both groups have been asked to complete a
survey that includes an assessment of likeability,
intention to use exercises and information, and
demographic indicators.
The main aim of the study is to prove a predicted
hypothesis that participants keep or even increase
their level of knowledge in elementary mathematics
by practising math problems provided by the
MatPort. In this way, we could conclude that the
MatPort actually supports enhancement in
elementary mathematics pedagogy.
5 CONCLUSIONS
In this paper, the instructional design of the MatPort
Web application, which is aimed for elementary
mathematics e-Learning in the active way, were
presented. We upgraded this design by incorporating
a high-performance evolutionary computation
method to support automatic search of relevant math
items. In this way, the MatPort may lead its users
toward higher scores in a thoughtful way. Finally,
we described the method for evaluation of the
application’s effectiveness.
After the pilot stage of the project, we are
planning to expand the dataset of math items to other
elementary school grades. We will increase its
efficiency through additional motivation tools, such
as winner lists or computer games, which will be
activated as soon as a student will gain a certain
score. Much work needs to be done to find an
adequate level of human intervention. In cooperation
with teachers, we will try to improve the way of
providing teaching instructions and intermediate
solutions. Last but not least, we will discuss the
problem of cheating.
In addition, we will do some experimental work
on the application of the efficient parameter-less
evolutionary search method (Papa, 2008) as a
substitution for the currently implemented genetic
algorithm.
ACKNOWLEDGEMENTS
This research project was supported by a joint action
of the Jožef Stefan Institute and the Educational
Research Institute Ljubljana under financial support
to education and training of the European Social
Fund.
The authors are most grateful to Breda Koroušič
for her guidance in the MatPort development. As an
experienced teacher of mathematics for many years
she has significantly contributed to the project,
providing a large collection of math items and all the
knowledge and experience gained through many
years of successful work with children.
REFERENCES
Bäck, T., 1996. Evolutionary Algorithms in Theory and
Practice. Oxford University Press.
Darie, C., Brinzarea, B., Chereches-Tosa, F., Bucica, M.,
2006. AJAX and PHP, PACKT Publishing.
Birmingham, 1
st
edition.
MATHPORT - Web Application to Support Enhancement in Elementary Mathematics Pedagogy
87

Bransford, J. D., Brown, A. L., Cocking, R. R. (Eds.),
2000. How People Learn: Brain, Mind, Experience,
and School. NATIONAL ACADEMY PRESS,
Washington, D.C., Expanded Edition.
Goldberg, D., 1989. Genetic Algorithms in Search,
Optimization, and Machine Learning. Addison-
Wesley.
Hayder, H., 2007. Object-Oriented Programming with
PHP5, PACKT Publishing. Birmingham, 1
st
edition.
Koroušić Seljak, B., 2006. Computer-based dietary menu
planning. WSEAS Transactions on Computers,
5(8):1650-1655.
Korošec, P., Šilc, J., 2008. Using stigmergy to solve
numerical optimization problems. Computing and
Informatics, 7 (3):377-402.
Papa, G., Koroušić Seljak, B., 2005. An artificial
intelligence approach to the efficiency improvement of
a universal motor. Engineering applications of
artificial intelligence, 18(1):47-55.
Papa, G., 2008. Parameter-Less Evolutionary Search. In
GECCO’08, Genetic and Evolutionary Computation
Conference: 1133-1134.
Tušar, T., Korošec, P., Papa, P., Filipič, B., Šilc, J., 2007.
A comparative study of stochastic optimization
methods in electric motor design. Applied Intelligence
27(2):101-111.
CSEDU 2009 - International Conference on Computer Supported Education
88
