
FOCUSING THE DIAGNOSIS FOR STUDENT MODELLING ON
AN INSTRUCTIONAL DESIGN
Angélica de Antonio, Jaime Ramírez
Facultad de Informática, Universidad Politécnica, Boadilla del Monte, Madrid, Spain
Julia Clemente
Departamento de Automática, Universidad de Alcalá, Campus Universitario, Alcalá de Henares, Spain
Keywords: Intelligent Tutoring System, Student Model, Cognitive Diagnosis, Non-monotonic reasoning.
Abstract: The advances in the educational field and the high complexity of student modelling have provoked it to be
one of the aspects more investigated in Intelligent Tutoring Systems (ITSs). The Student Models (SMs)
should not only represent the student’s knowledge, but rather they should reflect, as faithfully as possible,
the student’s reasoning process. To facilitate this goal, in this article a new approach to student modelling is
proposed that benefits from the advantages of Ontological Engineering, advancing in the pursue of a more
granular and complete knowledge representation. It’s focused, mainly, in the SM cognitive diagnosis
process, and we present a method based on instructional design, providing a rich diagnosis about the
student’s knowledge state –especially, about the state of learning objectives reached or not-, with non-
monotonic reasoning capacities, and supporting the detection and resolution of contradictions raised during
the reasoning on the student’s knowledge state. The main goal is to achieve SMs with a good adaptability to
the student’s features and a high flexibility for its integration in varied ITSs.
1 INTRODUCTION
The SM, core of ITSs, and, particularly, the
cognitive diagnosis process, has always been one of
the most important research lines in the area of ITSs
due to its complexity. Ohlsson (Ohlsson, 1986)
defines Cognitive Diagnosis (CD) like “the process
of inferring the cognitive state of a person starting
from their performance”. The difficulty in solving
this problem lies in giving an efficient answer to
important questions such as the following ones: what
types of knowledge about the student should be the
basis of the SM so that it can be adaptive to the
current individual characteristics of the student, and
the diagnosis process can provide more complete
information about the current cognitive state of the
student?, what characteristics should the SM
mechanisms have so that they can be applied to
several domains?, how to manage in the diagnosis
process the existence of inconsistencies that can
arise in the student’s performance throughout their
learning?, how to solve the diagnosis so that it does
not only allow to "detect" the state of the student's
knowledge but it also serves as an essential support
to the tutor to guide each individual student
appropriately during their learning?, etc. In order to
give proper answer to these questions, we present a
new Student Modelling mechanism based on
Ontological Engineering, a taxonomy to facilitate
the adaptation and extension of SM to different
types of ITSs and a rich diagnosis method with non-
monotonic reasoning capacities able to infer the state
of the learning objectives encompassed by the ITS
and correspondingly infer the student’s knowledge
state.
This article starts with some highlights about
Student Modelling and CD, proceeds with a
description of the adopted solution including the
ontology proposed for the SM, as well as the
diagnostic process, based on a set of diagnostic rules
and supported by a conflict manager. After an
application example, some conclusions put an end to
the paper.
2 STUDENT MODELLING IN ITS
So far, numerous approaches to SM have been
285
de Antonio A., Ramírez J. and Clemente J. (2009).
FOCUSING THE DIAGNOSIS FOR STUDENT MODELLING ON AN INSTRUCTIONAL DESIGN.
In Proceedings of the First International Conference on Computer Supported Education, pages 284-289
DOI: 10.5220/0001979902840289
Copyright
c
SciTePress

proposed in the field of ITS, representing different
information types (Petrushin, 1995), (Holt, 1994)
and using different methods to infer the student's
cognitive state. Most of the approaches to SM just
represent the state of the student’s knowledge about
the subject matter, including SMs that only represent
correct knowledge (Overlay or Differential Models)
and SMs that also represent wrong knowledge with
different approaches to the development of the error
library (Burton, 1982). A step forward are SMs that
also represent the student’s reasoning process,
which, according to Clancey (Clancey, 1986), can be
divided into Behavior simulation models, that only
describe the actions the student is carrying out, and
Functional simulation models, that describe the
student’s beliefs and goals.
In addition, some taxonomies for student's
knowledge modelling deserve to be highlighted by
their interesting contributions to this field. The
taxonomy of De Koning and Bredeweg (Koning,
1998), based on the multi-stratified framework
KADS (Wielinga, 1992), distinguishes as an added
knowledge level the strategic knowledge. Worth
mentioning is also the McCalla and Greer’s
taxonomy (McCalla, 1994), sustained in the idea of
granularity-based reasoning. However, most
approaches don't consider a complete taxonomy of
knowledge about the student; also, most of them
have validity only in certain domains or they are
hard to be adapted for different ITSs. At the same
time, most of them do not consider the student's
individual features to carry out a truly adaptive
teaching-learning process. Some exceptions are
(White, 1990), (Del Soldato, 1992), or the Chen and
Mizoguchi’s proposal (Chen, 2004), where an
ontology and an agent for SM are defined.
As far as Cognitive Diagnosis (CD) is concerned,
the evolution in the methods and techniques for
student modelling has forced the development of
new CD solutions. The first advances were based on
diagnostic methods coming from Artificial
Intelligence (AI). Other works, such as the Self
(Self, 1993), that uses the General Diagnosis Engine
(GDE) paradigm (De Kleer, 1989), helped to define
the nature of the CD problem, as a peculiar case of
device diagnosis in AI but with differences. Later,
an adapted version of GDE (Bredeweg, 1993),
sought to solve one of the problems outlined
previously by Self: defining a meta-diagnostic level.
However, the fundamental limitation of all these
approaches is that they try to apply model-based
techniques. Frequently, the student doesn't have an
only method for solving a problem, so there is not a
concrete a priori device model to be managed by the
cognitive diagnosis. In contrast, the decomposition-p
method (Tsybenko, 1995) allows generating the
associated models of the student that are used by the
CD during the problem resolution.
Another research line in the field of CD is
constituted by those methods that involve the student
in diagnosis to improve the system adaptability, such
as the collaborative student modelling (Bull, 1997),
scrutinized learner models (Kay, 1999), etc.
However, there are just a few methods that include
in their formulation the non monotonic nature of
reasoning about the student. Some exceptions are the
Ikeda et al.'s diagnosis system SMDS (Ikeda, 1993)
as well as the diagnosis system of the shell UMT
(Brajnik, 1994), supported both by an ATMS
(Assumption-based Truth Maintenance System).
Besides, in general, the CD methods are not able to
carry out a wide diagnosis that is based on a wide
student's taxonomy for the SM, integrating different
aspects like different types of demonstrated
knowledge, learning objectives that have been
reached, personal profile, traces of behaviour, etc.
3 PROPOSED SOLUTION
Our proposed solution for SM is based on a
pedagogical design approach (Figure 1). The design
of any ITS requires an instructional design for the
subject matter to be taught (X), which implies, in our
framework, defining a group of activities and the
objectives that the student should achieve in each
activity. For each activity that is effectively posed to
the student, the Expert module, using an automated
planner, will determine the steps or actions
(application of operators) that should be carried out to
conclude the activity successfully. Each operator
should have been defined with a set of preconditions
and consequences. The planner allows dynamic
construction of solution plans taking into account the
current state of the learning environment and the
possible student’s actions. When the student executes
a certain action (operator), this execution is registered
according to the SM ontology, which not only
contains different concepts but also relationships
among them, such as the ones that relate the learning
objectives (meaningful for the tutoring module) and
the knowledge objects (meaningful for the expert
module) that the student should acquire in order to be
able to reach those objectives. This relation is
fundamental given that it
allows inferring the concrete student’s knowledge
state (cognitive diagnosis) from the diagnosis of
reached or not learning objectives (pedagogical
diagnosis).
Based on what action the student performs and how
(registered during the activity in the execution
CSEDU 2009 - International Conference on Computer Supported Education
286

Add/Remove Data
PEDAGOGIC DIGNOSIS MODULE
Inference
Engine
CONFLICT SOLVER
STUDENT MODEL
Environment
Nogood
register
ATMS
Student/Tutor
Justifications
Control
Querys
Pedagogic
Diagnosis
Rules &
Contradiction Rules
Student/Tutor action
Heuristics:
Detection &
Resolution of
Contradictions
Student
Traces
Initial State
Objective state
Student
State
World
State
Student Profile
Knowledge Objects
Objectives
Traces
Student State
Ontology
Ontology
WORLD STATE
TUTORING MODULE
O1 ... Oi ... Op
EXPERT MODULE
Activity
D
Y
N
Á
M
I
C
Step1 Step2 ... Stepn
Operatorj
Planner
preconditions
postconditions
{
C1
C2
.
.
.
Cn
Knowledge
STUDENT MODULE
Learn X
S
T
Á
T
I
C
Activ1 Activ2 ... Activn
Objectives
Instructional design
Oi1 Oi2 ... Oiq
O1 ... Oi ... Op
Figure 1: Diagram of proposed student modelling.
trace included in the ontology) and on the objectives
that have already been reached or not when the
action is executed, the Pedagogic Diagnosis (PD)
module is responsible of determining the learning
objectives reached or not by the student. For that
purpose the PD uses a group of diagnostic rules.
During the diagnostic process diverse types of
contradictions can arise, and they must be solved by
the Conflicts Manager. This last capability will be
based on an ATMS system and a conflict solver
(CS).
The main steps of the proposed diagnosis
method are detailed below (Figure 1):
1. The initial state of the SM is established with
assumptions about the state of the learning
objectives (see section 3.2.1.).
2. The student executes an action in the context of
the learning activity he is carrying out.
Information could also come from the tutor if,
during the learning experience, he supplies a hint
or instructions, according to the tutoring strategy.
This step implies adding information to the SM
ontology regarding the trace, state and other
knowledge related to the action.
3. The characteristics of the specific action
executed by the student cause the triggering of
some diagnosis rules defined in the PD module.
By querying the SM ontology and an additional
ontology describing the current state of the
world, the PD module is responsible for inferring
which objectives are acquired or not by the
student. For this task, Jena forward chaining
inference engine has been chosen (Jena, 2006).
The inferences carried out by the PD module are
informed to the ATMS as justifications, and are
registered by it. If during the reasoning process
of the PD module a contradiction is detected,
then: a) The contradiction is communicated as a
justification to the ATMS, which obtains the
environment that supports the contradiction,
storing it in the so-called nogood register and b)
the PD module invokes the CS to solve the
contradiction. Different contradiction types,
depending on their cause, are solved differently,
based on certain heuristics defined by rules. CS
looks for candidate consistent environments
checking the assumptions that maintain the
inconsistency (nogood). The resolution of the
inconsistency will mean the modification, as
appropriate, of the objectives’ state in the SM
ontology.
4. The PD module continues the reasoning from the
updated state of the SM ontology.
3.1 Overview of the Ontology
The SM representation is based on ontologies, using
the OWL language and the Protégé tool. The Figure
2 shows some ontology’s outstanding hierarchies.
Student
_
Profile represents student's personal
information (demographic data, preferences,
physical and psychological features, etc.).
Learning
_
Objectives describes the learning
objectives defined for an educational process, at a
cognitive, psychomotor or affective level (De
Antonio, 2007).
Student
_
State describes the student’s
knowledge, their performance (regarding the
execution of activities, actions and associated
preconditions and postconditions, sessions,
trajectories throughout the learning environment,
etc.), their pedagogical state (regarding completion
of the learning plan, courses, activities, etc.), their
emotional state, and their general capacities and
competences (memory, attention, etc.).
FOCUSING THE DIAGNOSIS FOR STUDENT MODELLING ON AN INSTRUCTIONAL DESIGN
287
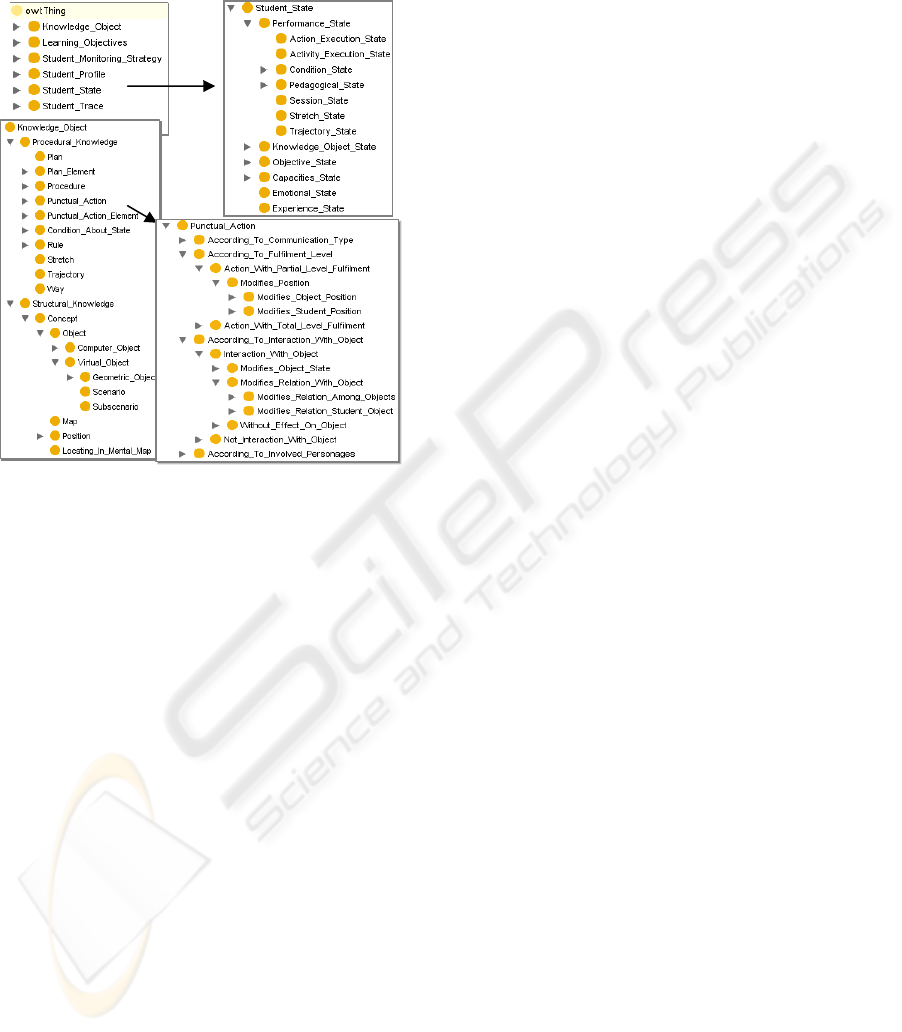
Student
_
Trace contains a temporal register of
the educational path (sessions, activities, actions,
trajectories, variables,etc.) and a historical register of
objective states.
Figure 2: Important hierarchies on SM’s ontology.
Knowledge_Object describes knowledge
elements involved in student’s learning. They can be
structural, such as concepts (e.g., objects present in a
3D environment), or procedural (actions and their
types, preconditions and postconditions, plans, etc.).
3.2 Pedagogic Diagnosis Rules
In the PD module, a set of rules to carry out the
diagnosis process is defined. These rules will infer
the state of learning objectives. When a rule infers
that the student has not achieved a certain objective;
the information that the SM provides on the student's
trace will be crucial to determine if the student has
forgotten some previously acquired knowledge or if
he has never achieved those objectives. The
pedagogic diagnosis rules match some rule patterns
according to a taxonomy of diagnosis criteria:
Diagnosis according to the type of action that a
student performs. These rules will infer the learning
objectives that can be assumed whenever the student
executes correctly/incorrectly a given action
depending on its relevancy and appropriateness (e.g.,
if the student picks up a designated visible object
correctly, it can be assumed that s/he is able to
recognize the appearance of the object). Other rule
patterns consider if the action is correctly executed
but it is not in the target sequence of actions; if the
action is in the plan but in the wrong order; if it is
impossible to execute the action because some of the
preconditions associated with the operator are not
met; if the student tries to apply the right operator
but to the wrong object; etc.
Diagnosis based on the number and type of
questions formulated by the student. These rules
infer the degree of knowledge that the student has of
the existent objects in the scenario, of the operators,
or of the activity itself, depending on the type of
questions posed by the student (what is this object
for? Where is the object X? What should I do next?
Why can’t I do this? What would it happen if I do
this?...).
As an example, let’s suppose that the student
executes an action on an object, a type of tray, which
is part of another object, a drawer, containing
several trays, but the tray on which the action has
been applied is not the correct one. According to the
established diagnosis criteria, this example could
match two patterns: a) an action involving
interaction with an object (tray), with coincidence of
the applied operator with the expected next one in
the plan (put in something), but without coincidence
of the objects to which the operator is applied, and
b) it is related to choosing the wrong part (tray) of an
object (drawer) that contains several parts.
) objy)) ,(objx' Of(Part
ChooseOfAbleIs SM(Add
objy) ,Of(objx'Part
objy) Of(objx,Part
)objx' Eq(objx,
)Plan(objx'ActNextObj
Plan(opx)ActNextOp
objx) Obj(opx,ToApply IF :R(b)
) ))Plan(objx'ActNextKnow(Obj
SM(Add
)objx' Eq(objx,
)Plan(objx'Act
NextObj
objx) Obj(opx,ToApply IF :R(a)
-
----
-
-
---
---
--
---
-
---
--
¬
⇒
∧
∧¬
∧
∧
∧
¬
⇒¬
∧
∧
(1)
The defined rules for those situations (1), deduce: a)
“The student does not know the object to be used in
the following action”, and b) “The student is not
able to choose the correct part (tray) of an object
(drawer).
3.2.1 ATMS Data Structures
The information about the student’s knowledge
inferred by the system is characterized by the lack of
completeness. The initial SM must be configured
with the assumed states for the objectives required
by the learning activity. An assumed objective state
can take the following values: true (the system
knows that the student achieved the objective), false
CSEDU 2009 - International Conference on Computer Supported Education
288

(the system knows that the student didn’t achieve the
objective) and unknown (the system doesn’t know
anything about the objective achievement). An
objective won’t be considered completely achieved
if the number of times it has been demonstrated
doesn’t reach a certain reliability threshold (these
values are established by properties of the concepts
Specific
_
Objective and Objective
_
State on the SM
ontology). The PD module informs the ATMS of the
initial objectives status with the following assumed
ATMS nodes:
>< }}
i
{{o}},
i
{{o),
i
state,
i
obj(objsup_state_
(2)
The first term of this triple represents the state
state
i
assumed for the objective obj
i
and o
i
is the
assumption identifier.
The firing of instantiated diagnostic rules during
the inference process is also informed to the ATMS
with the following justifications:
m
H...
1
H
i
H );
i
state,
i
(obj obj
-
state
i
θ
i
H ∧∧=⇒∧
~
~
(3)
)
i
r
exectime,
i
rplausible(
i
θ
-
=
(4)
θ
i
is an assumed node provided to the ATMS,
which may be retracted in the case of the CS needs
to annul the firing of the rule for solving an
inconsistency, and Hi is a fact in RDFS triple
format: (subject, predicate, object)). Moreover, the
contradiction rule fire is also input as justification of
ATMS.
3.2.2 Classification of Contradictions
The student’s behaviour, reflected through action
executions, tends to be inconsistent due to different
reasons, leading to inconsistencies in the objective
states. The contradiction causes are inferred by the
CS module by means of different types
heuristics.adapting the contradiction classification
given by (Chen, 2004):
Contradictions caused by non-monotonicity in
student’s behaviour or knowledge:
- Contradictions caused by changes in the student’s
mind. The student keeps acquiring new knowledge,
maybe giving rise to inconsistent objective states at
one particular moment. A tutor providing a hint or
an instruction could cause this contradiction type:.
change)mind (objx,ContradictType
)Hints(objxByObtained
true),State(objxCurrent (objx)Contradict IF
:ChangeMindRule
--
--
-
--
⇒
∧
(5)
- Contradictions caused by mistakes. Domain
dependent heuristics are defined in the PD module to
detect typical errors in each subject matter. Also,
domain independent heuristics can be defined to
distinguish the following types of contradictions
caused by mistakes: Contradictions caused by the
forgetting of knowledge and Contradictions caused
by oversights.
- Contradictions caused by the student’s own
inconsistent knowledge. This type of contradictions
is not detected at the moment in the method although
certain heuristics based on the analysis of objective
traces could be defined. They should not be resolved
(an effective tutoring strategy needs them).
- Contradictions caused by the student’s ignorance.
The student might behave sometimes apparently
randomly.
Contradictions caused by incorrect assumptions
adopted during the modelling: In the course of the
student’s learning process, some assumptions
regarding objective states deduced by the PD
module can become inconsistent.
3.2.3 Solving Contradictions
All contradictions except the ones caused by
inconsistent knowledge must be solved by the
method. The way of doing it is also based on
heuristics. Generally, the most recent objective state
in the contradiction is kept on the SM ontology,
although there are exceptions (e.g., if a contradiction
caused by a change in student’s mind is detected,
and later on another contradiction caused by
oversight is detected on the same objective, it would
be advisable to keep the previous state, not the most
current one).
4 DIAGNOSIS EXAMPLE
To demonstrate the solution proposed we have
designed a course to “Learn programming a washing
machine”. The possible operators for the course
activities have been defined as well as the concrete
objectives associated to them. The initially assumed
state for the objectives presented here is false (property
acquired=false) and this has been informed to the
ATMS as assumed nodes (see (2)). The activity 2 of
the course (phase 0), is being carried out by the student:
“Programming the washing machine with laundry
detergent”. When an action is executed by the student,
usually more than a PD rule is triggered, according to
the possible mappings with the SM ontology state, but
for brevity we will center here only in a pair of them.
The student, after executing some previous actions, has
put the washing powder in an incorrect tray, the bleach
tray in the detergents drawer (this drawer consists of 3
trays for washing powder, bleach and softener). As a
result, the rules R(a) and R(b) (1), among others, are
triggered and the ATMS is informed of the associated
FOCUSING THE DIAGNOSIS FOR STUDENT MODELLING ON AN INSTRUCTIONAL DESIGN
289

assumed node (3), and its corresponding justification
(4). Focusing on the first rule R(a), “The student does
not know the object to be used in the following action
(put in washing powder)” is inferred by R(a). An
assumed state for this objective was already stored in
the initial model of the SM ontology (Objective
_
State
→ Specific
_
Objective
_
State → state1, with its property
acquired=false). When the rule R(a) is fired, the action
on the consequent, Add
_
SM, causes the value of the
property levelCurrentReliability of state1 to be
increased in 1.
Afterwards, the tutoring strategy decides giving a
hint about the correct object with which the student
must interact (detergent tray). This tutor’s action
involves the firing of the rule (6). “The student knows
the object to be used in the following action” is
deduced as a result. For this objective, there was not an
instance in the ontology with property acquired=true.
The action Add
_
SM in this case sets to 1 the property
levelCurrentReliability. Likewise, the ATMS is
informed of the assumed node (3) and its justification
(4). A contradiction detection rule is triggered and the
ATMS is informed with the corresponding
justification. Also, the CS is invoked and one heuristic
rule (5) establishes the cause of the contradiction as a
change in the student’s mind and the contradiction is
resolved by keeping the more recent objective state
(acquired=true).
)precondx)) plan,act(next Precond(Req
SM(KnowAdd
precondx)) plan,act(next PrecondHints(ReqGive
) action)nextHints(typeGive IF :R(c)
---
-
----
---
⇒
∧
(6)
5 CONCLUSIONS
This article has described a solution based on
ontologies to student modelling in an ITS. The
general objective has been developing a SM with the
following main characteristics: genericity,
adaptability, non-monotonic diagnosis, extensibility
and reusability. The associated non-monotonic
diagnosis method has also been presented, relying
on an ATMS, the Jena framework and a pedagogic
diagnosis module.
REFERENCES
Brajnik, G., Tasso, C., 1994. A Shell for developing non-
monotonic user modelling systems. In International
Journal Human-Computer Studies, pp. 31—62.
Bredeweg, B. , Breuker, J., 1993. Device Models for
model-based diagnosis of student behaviour. In
Proceedings of AIED'93, pp.441–448.
Bull. S., 1997. Collaborative Student Modelling in Foreign
Language Learning. PhD thesis, U. of Edinburgh.
Burton R. R., 1982. Diagnosing bugs in a simple
procedural skill. In Intelligent tutoring systems. Ed.
Sleeman, D. H, pp. 157-184, Academic Press.
Chen, W., Mizoguchi, R., 2004. Learner Model Ontology
and Learner Model Agent. In Cognitive Support for
Learning –Imagining the Unknown, pp. 189-200.
Clancey, W. J., 1986. Qualitative student models. In
Annual Review of computer Science, Vol.1,pp.381-
450.
De Antonio, A., Ramírez, J., Clemente, J., 2007. A
proposal of Student Modelling Based on Ontologies.
In Proceedings of the 17
th
European-Japanese
Conference on Information Modelling and Knowledge
Bases, EJC 2007, pp. 302-309.
De Kleer, J., Williams, B. C., 1989. Diagnosing with
behavioral modes. In Proceedings of the International
Joint Conference on Artificial Intelligence, Detroit.
Del Soldato, T., 1992. Detecting and reacting to the
learner’s motivational state. 2nd International
Conference on Intelligent Tutoring Systems, Lecture
Notes in Computer Science, Vol. 608, pp. 567-574.
Holt, P., Dubs S., Jones, M., Greer, J., 1994. The State of
Student Modelling. In Student Modelling: The Key to
Individualized Knowledge-Based Instruction.
Springer-Verlag, pp. 3-39.
Ikeda, M., Kono, Y., Mizoguchi, R., 1993. Nonmonotonic
model inference. Proceedings of IJCAI’93, pp. 467-
473.
Jena-A semantic Web Framework for Java, 2006.
http://jena.sourceforge.net/index.html.
Kay, J. A., 1999. Scrutable User Modelling Shell for User-
Adapted Interaction. PhD thesis, University of Sydney
Koning, K., Bredeweg, B., 1998. Using GDE in
Educational Systems. 12nd International Workshop on
qualitative reasoning, pp. 42-49.
McCalla, G.I., Greer, J.E., 1994. Granularity-based
reasoning and belief revision in student models. In
Student Modelling: The key to Individualized
Knowledge-based instruction, eds. Greer, J.E. and
McCalla, G.I, Springer-Verlag, pp. 39-62.
Petrushin, V. A., 1995. Intelligent Tutoring Systems:
Architecture and Methods. In Journal of Computer
and Systems Sciences Internat., Vol. 33, No.1, pp.
117-139.
Self, J. A., 1993. Model-based cognitive diagnosis. User
Modeling and User-Adapted Interaction, Vol. 3, pp.
89-106.
Tsybenko, Y., 1995. Device Models in Student Modeling.
In Proceedings of AIED\'95, pp.525—532.
White, B., Frederiksen, J., 1990. Causal model progresions
as a foundation for intelligent learning environments. In
Artificial Intelligence, Vol. 42, pp. 52-121.
Wielinga, B. J. Schreiber, A. Th., Breuker, J. A., 1992.
KADS: A modelling approach to knowledge engineering,
vol. 4, No. 1, pp. 5-53.
CSEDU 2009 - International Conference on Computer Supported Education
290
