ENTERPRISE SYSTEM DEVELOPMENT WITH INVARIANT

PRESERVING

A Mathematical Approach by the Homotopy Lifting and Extension Properties

Kenji Ohmori

Faculty of Computer and Information Sciences, Hosei University, Koganei-shi,Tokyo184-8584, Japan

Tosiyasu L. Kunii

Morpho, Inc. The University of Tokyo, Entrepreneur Plaza 5F, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan

Keywords:

Homotopy, HLP, HEP, π-calculus, Abstraction hierarchy, Invariant preserving.

Abstract:

In this paper, a theoretical method for developing enterprise systems represented by the π-calculus is intro-

duced. The method is based on the modern mathematics of homotopy theory. The homotopy lifting and

extension properties are applied to developing systems in bottom-up and top-down ways with the incremen-

tally modular abstraction hierarchy, where system development is carried out by climbing down abstraction

hierarchy with adding invariants linearly. It leads to avoid combinatorial explosions causing an enormous

waste of time and cost on testing. The system requirements and a state transition diagram drive the actions

of an event by applying the HEP. Then, the state transition diagram and actions bring π-calculus processes by

applying the HLP. These processes do not need testing because of invariant preserving.

1 INTRODUCTION

Why are tests necessary in the development process

of enterprise systems? The Rational Uniﬁed Pro-

cess (RUP) widely used as an iterative software de-

velopment process framework includes tests as en-

gineering disciplines. The designers preferably us-

ing the RUP believe that tests are inevitable, while

knowing that much time and cost are spent on tests.

When developing systems by the RUP, system re-

quirements are modeled using the Uniﬁed Modeling

Language (UML) consisting of several kinds of dia-

grams including class, use-case and activity diagrams.

The individual-dependent and non-theoretical profes-

sional work from system requirements to UML dia-

grams leads to the necessity of tests. Activity dia-

grams and class diagrams are naturally different when

designers are different. How do you verify theoret-

ically that these different diagrams meet the system

requirements? Without showing the correctness of

modeling process, tests are required as the last tools

for veriﬁcation.

Invariants and invariant preserving are the most

important concepts in science. By deﬁning the

most abstract invariants ﬁrst and adding less abstract

or more speciﬁc invariants step by step with pre-

serving the previously added invariants, the correct-

ness of modeling process is guaranteed. The incre-

mentally modular abstraction hierarchy (IMAH) has

been introduced in these papers(Kunii, 2005), (Ku-

nii and Ohmori, 2006), (Ohmori and Kunii, 2006),

(Ohmori and Kunii, 2007a), (Ohmori and Kunii,

2007b), (Ohmori and Kunii, 2008a), (Ohmori and Ku-

nii, 2008b), where the IMAH has seven abstraction

levels from the homotopy level to the set theoretical

level, topological space level, adjunction space level,

cellular space level, presentation level and view level.

Invariants are added linearly while climbing down the

abstraction hierarchy. The IMAH has been applied

for architecture and modeling of cyberworlds.

On the way of climbing down the IMAH, methods

of top-down, bottom-up or mixture of them are re-

quired for architecture and modeling of systems. The

homotopy lifting property (HLP) and homotopy ex-

tension property (HEP) give theoretical backgrounds

(Havey, 2005), (Sieradski, 1992), (Spanier, 1966) for

a top-down and bottom-up method, respectively. Dif-

ﬁcult problems can be solved by a divide and conquer

116

Ohmori K. and L. Kunii T. (2009).

ENTERPRISE SYSTEM DEVELOPMENT WITH INVARIANT PRESERVING - A Mathematical Approach by the Homotopy Lifting and Extension

Properties.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Information Systems Analysis and Speciﬁcation, pages

116-123

DOI: 10.5220/0001981501160123

 SciTePress

method in computer science, where a difﬁcult prob-

lem is divided into two simple problems. The HLP

consists of a total, base and lifting space, where the

total space is complicated and is obtained in a bottom-

up way from two simple spaces of the base and lifting

space. As the HEP is dual to the HLP, the HEP gives

a top-down way.

In this paper, the energy purchase problem is de-

signed from its speciﬁcation to a model represented

by the π-calculus (Milner, 1999), (Sangiorgi and

Walker, 1999), (Hennessy, 2001) using the HLP and

HEP while climbing down the IMAH from the ab-

stract level of the system requirements to the spe-

ciﬁc level of a π-calculus model.@It is shown that the

most important concepts in this paper, that is, invari-

ants and invariant preserving are formally and theo-

retically described by modeling the energy purchase

problem (Havey, 2005) so that enterprise system de-

velopment is changed from a hand-made professional

job with testing to a theoretical and intelligent work

without testing.

2 MATHEMATICAL

BACKGROUNDS FOR

DEVELOPING ENTERPRISE

SYSTEMS

2.1 The Incrementally Modular

Abstraction Hierarchy

The IMAH has the following levels starting from

the most abstract to the most speciﬁc: the homo-

topy level; the set theoretical level; the topological

space level; the adjunction space level; the cellular

space level; the presentation level and the view level.

On the homotopy level, the most abstract invariants

with homotopyequivalenceare deﬁned using the HLP

or HEP. On the set theoretical level, sets of spaces,

which are mostly discrete, are deﬁned with logical

operations. On the topological space level, impor-

tant invariants with isomorphism is introduced. On

the adjunction level, invariants presenting the prop-

erties of dynamic changes, which are very important

characteristics for organizing the structure of infor-

mation, are deﬁned using adjunction mapping. On

the cellular space level, abstract physical structures

such as frameworks of state transition diagrams are

represented. On the presentation level, which is the

starting point in the traditional architecture and mod-

eling, designing entities such as UML diagrams and

concrete state transition diagrams are deﬁned. On the

view level, program codes including π-calculus pro-

cesses are obtained.

2.2 The Homotopy Lifting Property and

Homotopy Extension Property

The mathematical backgrounds for the HLP and HEP

are summarized as follows.

Def. 1: Continuous maps p, q are homotopic if there

exists a continuous map H : X × I → Y such that

H(x,0) = p(x) and H(x,1) = q(x), where I is the

unit interval [0,1]. H is called homotopy of p and

q, denoted by p ≃ q.

Def. 2: A continuous map λ : I → X yields a path.

λ(0) = x and λ(1) = y are called the initial and ter-

minal points. The path is denoted by w = (W,λ)

where W = λ(I).

Def. 3: A ﬁber bundle is a quadruple ξ = (E,B, F, p)

consisting of a total space E, a base space B, a

ﬁber F, and a bundle projection that is a contin-

uous surjection called F−bundle p : E → B such

that there exists an open covering U = {U} of B

and, for each U ∈ U , a homeomorphism called

a coordinate chart ϕ

: U × F → p

−1

(U) exists

such that the composite U × F → p

−1

(U) → U

is the projection to the ﬁrst factor U. Thus the

bundle projection p : E → B and the projection

: B × F → B are locally equivalent. The ﬁber

over b ∈ B is deﬁned to be equal to p

−1

(b), and we

note that F is homeomorphic to p

−1

(b) for every

b ∈ B, namely ∀b ∈ B,F

∼

−1

(b).

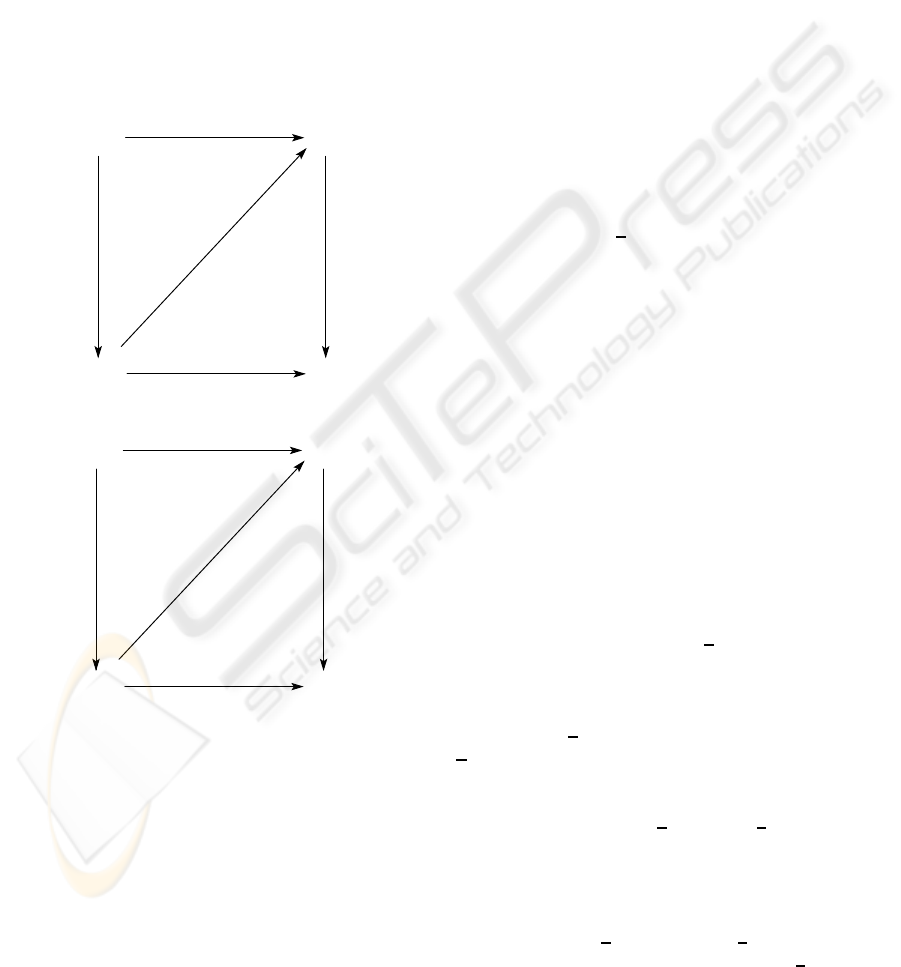
Def. 4: Given any commutative diagram of continu-

ous maps as shown in Fig. 1, the map p : E → B

has the homotopy lifting property if there is a con-

tinuous map

H : Y × I → E such that

H × i

= h

and p ◦

H = H. The homotopy

H thus lifts H

through p and extends h over i

where i

(a) =

(a,0).

Def. 5: A ﬁbration is a continuous map p : E → B

that has the homotopy lifting property.The homo-

topy extension property is dual to the homotopy

lifting property. The homotopy extension prop-

erty is deﬁned as follows.

Def. 6: Given any commutative diagram of continu-

ous maps as shown in Fig. 2, there is a contin-

uous map

K : X → Y

such that p

K = k and

K × i = K. The homotopy

K thus extends K over

i and lifts k through p

where p

(λ) = λ(0).

Def. 7: An inclusion of a closed subspace i : A ֒→ X

is a coﬁbration if i has the homotopy extension

property. Y

is the path space on Y. The path

space is deﬁned as follows.

ENTERPRISE SYSTEM DEVELOPMENT WITH INVARIANT PRESERVING - A Mathematical Approach by the

Homotopy Lifting and Extension Properties

117

Def. 8: The path space on X, denoted X

, is the

space {λ : I → X|continuous} endowed with the

compact-open topology.

Def. 9: Let us start with a topological space X and

attach another topological space Y to it. Then,

= Y ⊔

X = Y ⊔X/ ∼ is an adjunction space ob-

tained by adjunctingY to X by an adjunction map,

f (or by identifying each point y ∈ Y

| Y

⊂ Y with

its image f(y) ∈ X by a continuous map f). ⊔

denotes a disjoint union. The adjuncting map f

is a continuous map such that f : Y

→ X, where

⊂ Y. Thus, the adjuncting space Y

= Y ⊔X/ ∼

is a case of quotient spaces

Y ⊔ X/ ∼= Y ⊔

X = Y ⊔ X/(x ∼ f(y) | ∀y ∈ Y

Y × I

Figure 1: Homotopy Lifting Property.

Figure 2: Homotopy Extension Property.

3 APPLYING THE HOMOTOPY

THEORY TO AN ENERGY

PURCHASE PROBLEM

3.1 An Energy Purchase Problem

The energy purchase@problem is shown in the book

(Havey, 2005). The outline of this problem is as fol-

lows. A customer is registerd to an energy supplier.

The customer ordinarily buys energy from the energy

supplier. Because of deregulation, the customer is al-

lowed to buy energy from a retailer. As there are sev-

eral retailers, the custome is also allowed to switch

retailers. When the customer wants to switch retail-

ers, he has to notify the energy supplier of a retailer

switch and the energy supplier reports this switch to

the retailers. The customer also switches back to the

energy supplier

3.2 The π-calculus Process

The π-calculus is a parallel processing model where

communication links are dynamically changed. The

action preﬁxes π are a generalization of actions. An

action preﬁx expresses either sending or receiving a

message or making a silent transition. The π-preﬁxes

are deﬁned as follows.

π ::= x(y) receive y along x

::= x(y) send y along x

::= τ unobservable action

The set P

of π-calculus process expressions is de-

ﬁned as follows:

P ::= 0 |

∑

λ∈Λ

| P

| new a P | !P

0 is an inaction process that can do nothing. The pro-

cesses

∑

λ∈Λ

are called sums. Each item is a pro-

cess and only one item is executed. Λ is any ﬁnite

indexing set. In a sum

∑

λ∈Λ

, it is said that P

guarded by π

since the action by π

has to proceed

before P

becomes active. P

can proceed indepen-

dently and interact by shared names. new a P restricts

the scope of the name a to P. !P repeats P inﬁnitely.

Two examples are given for explaining the π-

calculus. The ﬁrst example x(y).P

|x(z).P

shows

how a message is sent via a communication link.

x(y) of an action preﬁx π can receive any name and

y is bounded to the name or substituted by the re-

ceived name. x(y).P

|x(z).P

executes two processes.

x(y).P

, where x is used as a communication link,

sends y via x. x(z).P

receives y via x where z is sub-

stituted by y.

The second example x(y).P

|x(z).z(u).P

|y(w).P

shows how a communication link is dynamically

changed. The ﬁrst process notiﬁes the second process

of a communication link name, which will be used by

the second process for communicating with the third

process. That is, x(y).P

and x(z).z(u).P

changes a

message like the above explanation. x(z).z(u).P

re-

ceives y via x, it sends u via y since z is bounded to y.

Finally, y(w).P

receives u via y.

ICEIS 2009 - International Conference on Enterprise Information Systems

118

3.3 A Hep Application

The energy purchasing problem is solved by the fol-

lowing steps.

1) A state transition diagram is obtained by climb-

ing down from the homotopy level to the presentation

level.

2) Using the HEP, the actions for an event caus-

ing a situation change are obtained from the system

requirements and the state transition diagram. The

actions are also generated by climbing down the ab-

straction hierarchy.

3) Using the HLP, the processes for the energy

purchase problem are obtained.

At ﬁrst, the system requirements are formed as a

topological space. Assuming that there are one cus-

tomer, one energy supplier and two suppliers without

losing generality, the system requirements consist of

the following elements.

: The customer ordinarily buys energy from the

energy supplier.

: The customer can buy energy from a retailer.

: When the customer changes his purchasing

place from the supplier to a retailer, he has to notify

the supplier of his enrollment.

: When the customer changes his purchasing

place from a retailer to another retailer, he has to no-

tify the supplier of his switch.

: When a customer changes his purchasing

place from a retailer to the supplier, he has to notify

the supplier of his drop.

The set of these elements forms a topological

space by introducing discrete topology.

A state transition diagram is constructed by ex-

tracting states and transitions from the system require-

ments. This process is achieved by providing two ab-

stract states, e

for purchase on standard supply and

for purchase by taking advantage of deregulation

and three state transitions, e

from e

to e

caused by

an enrollment, e

from e

to e

by a drop and e

from

to e

by a switch. As states and transitions are or-

dinary represented as vertexes and edges, e

and e

are deﬁned as 0-dimensional spaces and e

and e

as 1-dimensional spaces. The set of {e

}

is formed as a topological space by introducing dis-

crete topology. States and transitions are connected to

form a state transition diagram by applying adjunct-

ing maps. For this problem, both boundaries of ∂e

are attached to e

and e

. In the same way, the bound-

aries of other state transitions are attached to the cor-

responding states.

To form the state transition diagram as a CW-

complex, two 2-dimentional spaces: e

and e

, are

provided and these boundaries are attached to the cor-

responding edges. The CW complex is further trans-

formed to a more speciﬁc state transition diagram

on the presentation level as shown in Fig. 3. The

state transition diagram is a subset of the system re-

quirements where e

and e

correspond to

and x

, respectively.

Enroll

Drop

Switch

Supplier

Retailer

The cellular space level

The presentation level

Figure 3: State transition diagram.

The energy purchasing problem has three situations:

for purchasing from the energy supplier,Z

for pur-

chasing from retailer A and Z

for purchasing from

retailer B. Sometimes, a situation is called a use-

case. As the customer is allowed to change a pur-

chasing place, the sequence of situations generated by

changing purchase places is represented in the form of

)

∗

)

∗

. One example sequence is shown from

Fig. 4 to Fig. 7. The change of a purchasing place

is caused by events such as an enrollment, switch and

drop. Each of them has a series of actions.

Now, let’s consider obtaining actions in an event

using the HEP. Later, the actions are transformed into

π-processes. In the HEP, X is the system requirements

and A is the state transition diagram. Y is a series of

actions for an event. There are three events: enroll-

ment E

, switch E

and drop E

. E

, E

and E

cause

transitions of Z

→ Z

, Z

→ Z

and Z

→ Z

, respectively. Each event has a

series of actions such that Y

= Y × E

has {1) Mike

notiﬁes Sup of the purchase enrollment to RetA, 2)

Sup receives from Mike the purchase enrollment to

RetA, 3) Sup reports to RetA the purchase enroll-

ment of Mike, 4) RetA receives from Sup the pur-

ENTERPRISE SYSTEM DEVELOPMENT WITH INVARIANT PRESERVING - A Mathematical Approach by the

Homotopy Lifting and Extension Properties

119

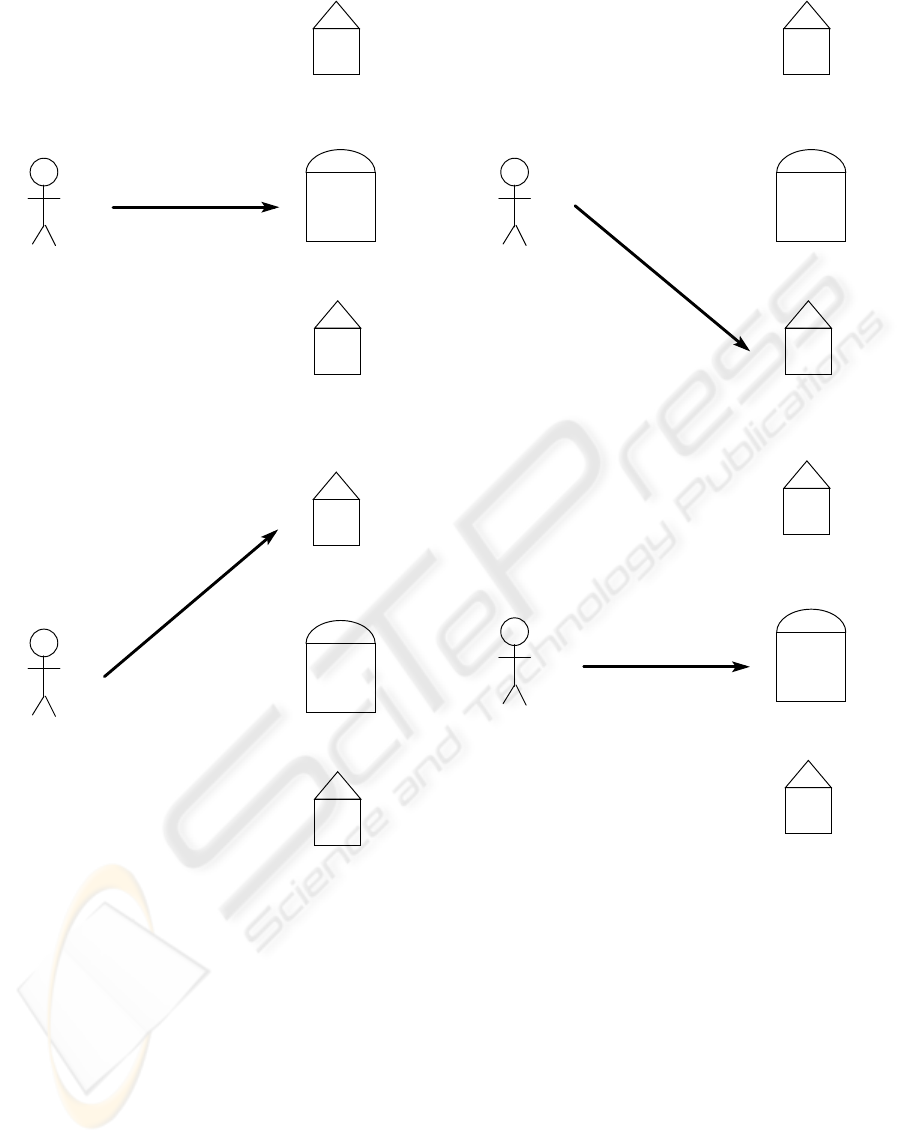
Retailer A

Retailer B

Supplier

Customer

Standard supply

Figure 4: Customer is not enrolled with a retailer, on stan-

dard supply.

Retailer A

Retailer B

Supplier

Customer

Enroll A

Figure 5: Customer enrolls with retailer A.

chase enrollment of Mike} where the customer, the

energy supplier and two retailers are represented by

Mike,Sup,RetA and RetB. Actions are obtained from

the system speciﬁcation. In the above case, x

deﬁnes

its actions.

For each event, the following actions are obtained.

1. Event: Y

(Purchase change from the energy

supplier to a retailer)

1) Sub event: Y

(Change from Sup to RetA)

: Mike notiﬁes Sup of a purchase enrollment

to RetA.

: Sup receives from Mike a purchase enroll-

ment to RetA.

Retailer A

Retailer B

Supplier

Customer

Switch B

Figure 6: Customer switches to retailer B.

Retailer A

Retailer B

Supplier

Customer

Drop B, back to

Supplier

Figure 7: Customer drops retailer, back to standard supply.

: Sup reports to RetA a purchase enrollment of

Mike.

: RetA receives from Sup a purchase enroll-

ment of Mike.

2) Sub event: Y

(Change from Sup to RetB)

: Mike notiﬁes Sup of a purchase enrollment

to RetB.

: Sup receives from Mike a purchase enroll-

ment to RetB.

: Sup reports to RetB a purchase enrollment of

Mike.

: RetB receives from Sup a purchase enroll-

ment of Mike.

ICEIS 2009 - International Conference on Enterprise Information Systems

120

2. Event: Y

(Purchase change among retailers)

1) Sub event: Y

(Change from RetA to RetB)

: Mike notiﬁes Sup of a purchase switch from

RetA to RetB.

: Sup receives from Mike a purchase switch

from RetA to RetB.

: Sup reports to RetA a purchase drop of Mike.

: Sup reports to RetB a purchase enrollment of

Mike.

: RetA receives from Sup a purchase drop of

Mike.

: RetB receives from Sup a purchase enroll-

ment of Mike.

2) Sub event: Y

(Change from RetB to RetA)

: Mike notiﬁes Sup of a purchase switch from

RetB to RetA.

: Sup receives from Mike a purchase switch

from RetB to RetA.

: Sup reports to RetB a purchase drop of Mike.

: Sup reports to RetA a purchase enrollment of

Mike.

: RetB receives from Sup a purchase drop of

Mike.

: RetA receives from Sup a purchase enroll-

ment of Mike.

3. Event: Y

(Purchase change from the retailer to

the energy supplier)

1) Sub event: Y

(Change from RetA to Sup)

: Mike notiﬁes Sup of a purchase drop out of

RetA.

: Sup receives from Mike a purchase drop out

of RetA.

: Sup reports to RetA a purchase drop of Mike.

: RetA receives from Sup a purchase drop of

Mike.

2) Sub event: Y

(Change from RetB to Sup)

: Mike notiﬁes Sup of a purchase drop out of

RetB.

: Sup receives from Mike a purchase drop out

of RetB.

: Sup reports toRetB a purchase drop of Mike.

: RetB receives from Sup a purchase drop of

Mike.

Let’s consider constructing Y

. The interval I is rep-

resented by (E

∗

)

∗

. Y

is a set of paths, each of

which is the sequence of the i

action along I such

that

= { ((y

)(y

)

∗

))

∗

((y

)(y

)

∗

((y

))

∗

,...}.

However, a path yielded by Y

is not allowed to in-

clude y

and y

where m 6= n, and y

and

where m = n as it part.

It is not hard to show that A is included in X, K

and

K are homotopies and

K extends K over i.

3.4 A HLP Application

Now, consider obtaining π-calculus processes of the

energy purchase problem using the HLP where B and

Y × I are described as a state transition diagram and

events, and π-calculus processes are accommodated

in E. E consists of layers for agents in the energy pur-

chasing problem, where the customer, supplier and

customers are agents. When solving this problem, the

agent for the customer is categorized into two types:

the customer purchasing on standard supply and the

customer purchasing from a retailer. The obtained

processes are shown from Fig. 8 to Fig. 11, where

there are four processes: P

for the supplier, P

for re-

tailers, P

for the customer on standard supply and P

for the customer purchasing from retailer. Each pro-

cess is represented in the same CW-complex on the

cellular space level as the state transition diagram.

= enroll(ret,cus)ret(Add,cus).P

ret2(Add,cus).P

= drop(ret,cus)ret(Drop,cus).P

ret1(Drop,cus)

= switch(ret1,ret2, cus)

Supplier

Retailer

Figure 8: Process for the supplier.

= ret(mesg,cus).P

Supplier

Retailer

Figure 9: Process for the retailers.

ENTERPRISE SYSTEM DEVELOPMENT WITH INVARIANT PRESERVING - A Mathematical Approach by the

Homotopy Lifting and Extension Properties

121

+ebroll(RetB, Mike).P

(RetB)

= enroll(RetA,Mike).P

(RetA)

Supplier

Retailer

Figure 10: Process for the customer on standard supply.

(RetB) =

(RetA) = drop(RetA,Mike).P

(RetB) = drop(RetB,Mike).P

(RetA) =

switch(RetA,RetB,Mike).P

(RetB)

switch(RetB,RetA,Mike).P

(RetA)

Supplier

Retailer

Figure 11: Process for the customer purchasing from a re-

tailer.

However, these are different on the presentation level.

Arcs of the presentation level are obtained from the

events as follows. Firstly, Y

is mapped into these

state diagrams. As Y

has two subspaces Y

and

, both of them are mapped step by step in the

following way. y

that is an element of Y

mapped as a process enroll(RetA,Mike). P4(RetA)

for the customer purchasing on standard sup-

ply. y

and y

are mapped as a process

enroll(ret,cus).ret(Add,cus). P1 for the supplier. y

is mapped as a process ret(message, cus). P2(ret) for

the retailer. Other mappings are carried out in the

same way for all events. It is not also hard to prove

that H and

H are homotopies and

H lifts H through

4 REFINEMENT STEPS

A state diagram is a connected CW-complex that is

homotopy equivalent to a point. If a state transition

diagram is reduced to a point, then the processes dis-

tributed on arcs are assembled into a single expres-

sion. The processes for the supplier, retailers, cus-

tomer on standard supply and customer purchasing

from a retailer are obtained by the following expres-

sions.

= enroll(ret,cus)ret(Add,cus)

+switch(ret1,ret2, cus))

ret1(Drop,cus)ret2(Add,cus)

+drop(ret,cus)ret(Drop, cus)).P

= ret(mesg,cus).P

∑

ret∈{RetA,RetB}

enroll(ret,Mike).P

(ret).

(ret1) =

∑

ret2∈{RetA,RetB}∩(ret16=ret2)

switch(ret1,ret2, Mike).P

(ret2)

+drop(ret1,Mike).P

where ret1 ∈ {RetA,RetB}.

The generalized expression is also obtained using the

HLP. When the problem is extended to have several

customers and retailers, the above processes are gen-

eralized from the HLP as follows, where Cus and Ret

are the sets of the customers and retailers and cus and

ret1 are elements of Cus and Ret, respectively.

(cus) =

∑

ret∈Ret

enroll(ret, cus).P

(cus,ret).

(cus,ret1) =

∑

ret2∈Ret∩(ret16=ret2)

switch(ret1,ret2, cus).P

(cus,ret2)

+drop(ret1,cus).P

(cus).

5 CONCLUSIONS

A new development method using homotopy theory

has been introduced. The HEP and HLP are the most

abstract and powerful tools for categorizing mathe-

matical objects. Homotopy equivalence are main-

tained within the HEP and HLP. In this paper, the

HEP and HLP have been introduced for establishing

fundamentals in software science. Architecture, mod-

eling and designing are performed by climbing down

the abstraction hierarchy adding invariants incremen-

tally using the HEP and HLP. The IMAH has 7 lev-

els from the homotopy space level to the set theoret-

ical level, the topological space level, the adjunction

level, the cellular space level, presentation level and

the view level. The system requirements for the en-

ergy purchase problem on the set theoretical level is

transformed to the π-calculus processes on the view

ICEIS 2009 - International Conference on Enterprise Information Systems

122

level using the HEP and HLP. While climbing down

the abstraction hierarchy, invariants are incrementally

added from abstract to speciﬁc ones while keeping

homotopy equivalence on all levels and topological

equivalence on less abstract levels than topological

space level. The invariant preserving by homotopy

equivalence and topological equivalence makes test

unnecessary and enables to avoid combinatorial ex-

plosions that the conventional method is facing now.

The HEP and HLP have been introduced for a

top-down and bottom-up design, respectively. This

is a new application ﬁeld of the HEP and HLP. When

solving the energy purchase problem, the state transi-

tion diagram and events, which are speciﬁc modeling

and designing entities from the system requirements

on the set theoretical level, have been obtained using

the HEP in a top-downway, where the system require-

ments, state transition diagram and events are homo-

topy equivalent. Then, the π-calculus processes on

the view level have been obtained from the state tran-

sition diagram and events using the HLP in a bottom-

up way. The introduced method gives a mathemati-

cal foundation for a top-down and bottom-up design,

which are carried out by individual know-how in the

conventional system. The top-down and bottom-up

design also keeps invariants with making tests neces-

sary.

The development steps introduced here start from

the system requirements, move to obtain the state

transition diagram and actions for events and end with

the π-calculus processes. These operations are au-

tomatic. By developing a development framework

along these steps, the development of enterprise sys-

tems will be automated from the system requirements

to its BPEL codes.

This paper has constructed a bridge between com-

puter science and the modern mathematics of homo-

topy theory. The introduced method is general and

applicable to any ﬁelds of computer science includ-

ing computer graphics, computer architecture, net-

work architecture and cyberworlds. In this paper, the

π-calculus is used to express processes for enterprise

systems. It is easily applicable to communicating se-

quential processes, which is another process algebra

and powerful tools in the ﬁeld of embedded systems.

REFERENCES

Havey, M. (2005). Essential Business Process Modeling.

O’Reilly Media, Inc, Cambridge.

Hennessy, M. (2001). A Distributed Pi-Calculus. Cam-

bridge University Press, Cambridge.

Kunii, T. L. (2005). Cyberworlds -theory, design and

potetial-. The Transactions of The Institute of Elec-

tronics, Information and Communication Engineers,

E88-D(5):790–800.

Kunii, T. L. and Ohmori, K. (2006). Cyberworlds: Ar-

chitecture and modeling by an incrementally mod-

ular abstraction hierarchy. The Visual Computer,

22(12):949–964.

Milner, R. (1999). Communicating And Mobile Systems:

Pi-Calculus. Cambridge University Press, Cam-

bridge.

Ohmori, K. and Kunii, T. L. (2006). An incrementally mod-

ular abstraction hierarchy for linear software develop-

ment methodology. Int. Conf. on Cyberworlds 2006,

pages 216–223.

Ohmori, K. and Kunii, T. L. (2007a). Development of an

accounting system. ICEIS2007, pages 437–444.

Ohmori, K. and Kunii, T. L. (2007b). The mathematical

structure of cyberworlds. Int. Conf. on Cyberworlds

2007, pages 100–107.

Ohmori, K. and Kunii, T. L. (2008a). Mathematical model-

ing of ubiquitous systems. Int. Conf. on Cyberworlds

2008, pages 69–74.

Ohmori, K. and Kunii, T. L. (2008b). A pi-calculus model-

ing method for cyberworlds systems using the duality

between a ﬁbration and a coﬁbration. Int. Conf. on

Cyberworlds 2008, pages 363–370.

Sangiorgi, D. and Walker, D. (1999). The Pi-Calculus: A

Theory of Mobile Processes. Cambridge University

Press, Cambridge.

Sieradski, A. J. (1992). An introduction to topology and

homotopy. PWS-Kent Publishing Company, Boston.

Spanier, E. H. (1966). Algebraic topology. Springer-Verlag,

New York.

ENTERPRISE SYSTEM DEVELOPMENT WITH INVARIANT PRESERVING - A Mathematical Approach by the

Homotopy Lifting and Extension Properties

123