T
OWARDS A UNIFIED DOMAIN FOR FUZZY TEMPORAL
DATABASES
M. C. Garrido
Junta de Andaluca, Spain
N. Mar
´
ın and O. Pons
Dept. of Computer Science and Artificial Intelligence, University of Granada, ETSI Inform
´
atica, Spain
Keywords:
Fuzzy data, Temporal database, Fuzzy interval, Data manipulation.
Abstract:
Temporal Databases (TDB) have as a primary aim to offer a common framework to those DB applications
that need to store or handle temporal data of different nature or source, since they allow to unify the concept
of time from the point of view of its meaning, its representation and its manipulation. At first sight, it may
seem that incorporation of time to a DB is a direct and even simple task, but, on the contrary, it is a quite
complex aim because time may be provided by different sources, with different granularities and meaning.
The situation gets more complex when the time specification is not made in precise but in fuzzy terms, where
together with the inherent problems of the time domain, we have to consider the imprecision factor. To deal
with this problem, the first task to perform is to unify as much as possible the representation of time in order
to be able to define the range and the semantics of the necessary operators to handle data of this type.
1 INTRODUCTION
1.1 Previous Concepts
Temporal Databases, in the widest sense, offer a com-
mon framework for all database applications that in-
volve some temporal aspects when organizing data.
These databases allow to unify the time concept from
several points of view: the representation, the seman-
tics and the manipulation.
Database applications involving temporal data are
not a new subject. In fact, they have been devel-
oped since the relational databases began to be used,
but applications programmers were responsible for
designing, representing, programming and managing
the necessary temporal concepts.
Temporal Databases (from now on TDB) have
partially solved the problem because they provide
data types and operators for handling time.
From the point of view of the real world, there ex-
ist two basic ways for associating temporal concepts
to a fact:
1. Punctual facts: a fact is related to an only time
mark that depends on the granularity and informs
about the time when it happened. As instances,
birthdays, the date for an order, an academic year,
...
2. Time periods: that are represented by a starting in-
stant and an ending one, so the duration (or valid
time) of the fact is implicit. Some examples are:
[admission date, discharge date], [start contract
date, end contract date], ...
This way of time interpretation is called valid
time.
In the valid time relation EMP (see fig. 1) each
tuple represents a version for the available informa-
tion about an employee, and this version is valid only
when used in the time interval [VST,VET]. The up-
to-date version, also called valid tuple, is undefined-
valued in the attribute VET (a special value).
Sometimes it is not possible for the user to give
an exact but an imprecise starting/ending point for the
validity period of a fact. This is the case, for example,
when a patient does not exactly know when a concrete
ailment or symptom started. In this case, the use of
fuzzy sets theory is necessary for not missing such
important information since fuzzy time values could
be defined (Barro et al., 1994). This situation give
355
C. Garrido M., Marín N. and Pons O. (2009).
TOWARDS A UNIFIED DOMAIN FOR FUZZY TEMPORAL DATABASES.
In Proceedings of the 11th International Conference on Enterprise Information Systems - Information Systems Analysis and Specification, pages
355-358
DOI: 10.5220/0001982603550358
Copyright
c
 SciTePress

Undefined15-06-1997987740006579STREEP
10-08-200801-05-2005458828001278BROWN
Undefined01-04-1997998922009877REDFORD
31-03-199701-02-1996458815009877REDFORD
31-01-199620-08-1994458812009877REDFORD
Undefined01-06-1998987718001245GRANT
31-05-199815-06-1997987715001245GRANT
VETVSTBOSSSALARYEMPIDEMPNAM
Undefined15-06-1997987740006579STREEP
10-08-200801-05-2005458828001278BROWN
Undefined01-04-1997998922009877REDFORD
31-03-199701-02-1996458815009877REDFORD
31-01-199620-08-1994458812009877REDFORD
Undefined01-06-1998987718001245GRANT
31-05-199815-06-1997987715001245GRANT
VETVSTBOSSSALARYEMPIDEMPNAM
Figure 1: Instance example of the valid time relation EMP.
rise to a large number of new problems (Bettini et al.,
1998), and this paper is devoted to the definition of
time domain that allows the representation of different
fuzzy time specifications.
1.2 Previous Concepts on Fuzzy Sets
A fuzzy value is a fuzzy representation about the real
value of a property (attribute) when it is not precisely
known.
In this paper, according to Goguen’s Fuzzification
Principle (Goguen, 1967), we will call every fuzzy
set of the real line fuzzy quantity. A fuzzy number is a
particular case of a fuzzy quantity with the following
properties:
Definition 1.-
The fuzzy quantity A with membership function
µ
A
(x) is a fuzzy number (Dubois and Prade, 1987)
iff:
1. ∀ α ∈ [0, 1], A
α
= {x ∈ R | µ
A
(x) ≥ α} (α-cuts of
A) is a convex set.
2. µ
A
(x) is an upper-semicontinuous function.
3. The support set of A, defined as Supp(A) = {x ∈
R | µ
A
(x) > 0}, is a bounded set of R, where R is
the set of real numbers.
We will use
∼
R
to denote the set of fuzzy numbers,
and h(A) to denote the height of the fuzzy number A.
For the sake of simplicity, we will use capital letters at
the beginning of the alphabet to represent fuzzy num-
bers.
The interval [a
α
, b
α
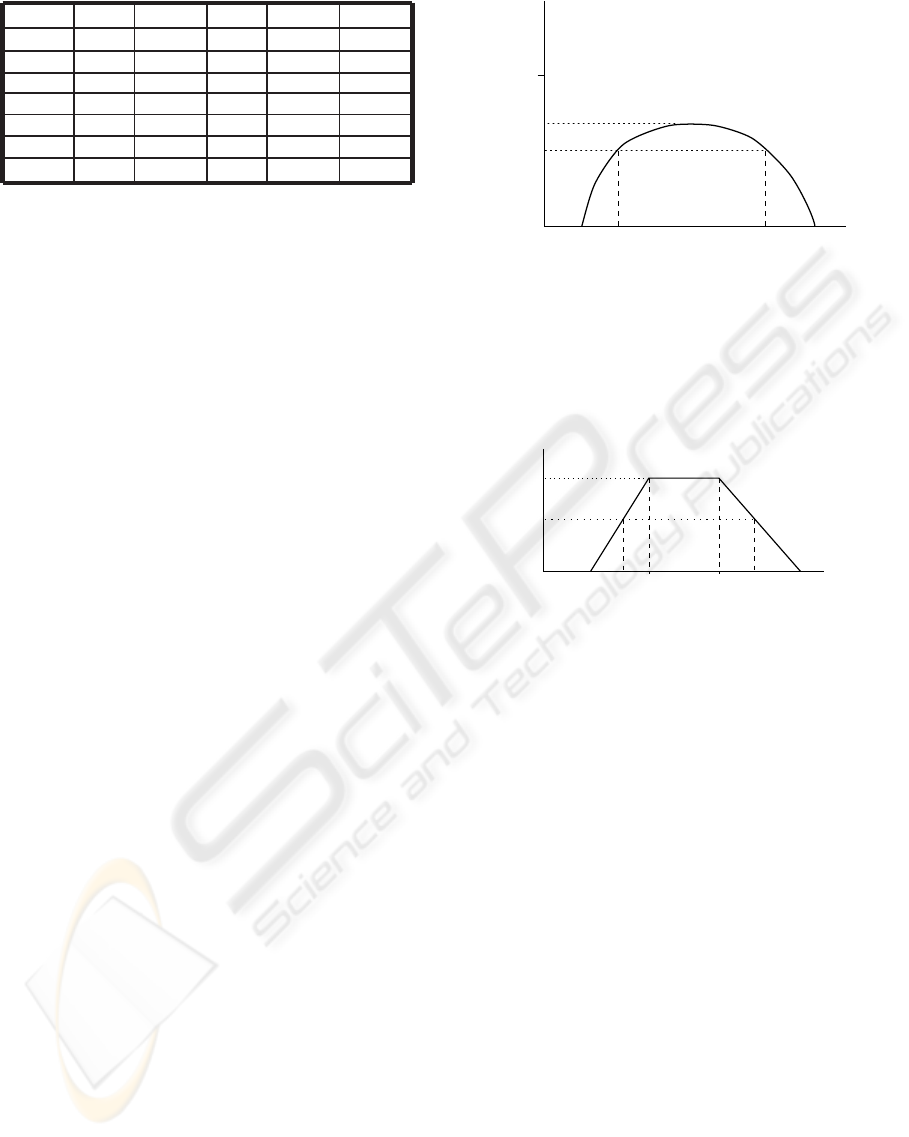
] (see figure 2) is called the α-
cut of A. So then, fuzzy numbers are fuzzy quantities
whose α-cuts are closed and bounded intervals: A
α
=
[a
α
, b
α
] with α ∈ (0, 1].
If there is, at least, one point x verifying µ
A
(x) = 1
we say that A is a normalized fuzzy number.
Sometimes, a trapezoidal shape is used to repre-
sent fuzzy values. This representation is very useful
as the fuzzy number is completely characterized by
four parameters (m
1
, m
2
, a, b) as shows figure 3 and
the height h(A) when the fuzzy value is not normal-
ized. We will call modal set all values in the interval
A
h(A)
α
1
α
ba
α
Figure 2: Fuzzy number.
[m
1
, m
2
], i.e, the set {x ∈ Supp(A) | ∀ y ∈ R, µ
A
(x) ≥
µ
A
(y)}. The values a and b are called left and right
spreads, respectively.
In our approach, we will use trapezoidal and nor-
malized fuzzy values.
A
m −a m
α
a
α α
m
2
m +b
1 1 2
b
1
Figure 3: Trapezoidal fuzzy number.
2 FUZZY TIME
REPRESENTATION
2.1 Imprecision Measure on Fuzzy
Values
As pointed out in the previous section, we are going
to translate fuzzy uncertainty into imprecision under
certain conditions. The most important of these con-
ditions is that the amount of information provided by
the fuzzy number remains equal before and after the
transformation. So then, the first step is to define an
information function for fuzzy numbers.
In (Gonz
´
alez et al., 1999) we propose an ax-
iomatic definition of information, partially inspired in
the theory of generalized information given by Kamp
´
e
de F
´
eriet (de Feri
´
et, 1973) and that can be related to
the precision indexes (Dubois and Prade, 1987) and
the specificity concept, introduced by Yager in (Yager,
1981).
Definition 1.-
Let D ⊆
∼
R
| R ⊆ D ; we say that the application I
defined as:
ICEIS 2009 - International Conference on Enterprise Information Systems
356

I : D −→ [0, 1]
is an information on D if it verifies:
1. I(A) = 1, ∀ A ∈ R
2. ∀ A, B ∈ D | h(A) = h(B) and A ⊆ B =⇒ I(B) ≤
I(A).
The information about fuzzy numbers may depend
on different factors, in particular, on imprecision and
certainty (Chountas and Petrounias, 2000). We focus
on general types of information related only to these
two factors.
To compute a measure of the imprecision con-
tained in a fuzzy number, we will consider a measure
of the imprecision of its α-cuts, which are closed in-
tervals on which the following function is defined:
∀ A ∈
∼
R
, f
A
(α) =
½
b
α
− a
α
i f α ≤ h(A)
0, otherwise
From this imprecision function on the α-cuts, we
define the total imprecision of a fuzzy value as a com-
bination of the imprecision in every level α. When
α = 0, we will consider that f
A
(0) is the length of the
support set.
Definition 2.-
The imprecision of a fuzzy number is defined as
follows:
f :
∼
R
−→ R
+
0
∀ A ∈
∼
R
, f (A) =
Z
h(A)
0
f
A
(α) dα
That is, the imprecision function f coincides with
the area below the membership function of the fuzzy
value. Since we are considering that fuzzy time values
are always normalized, then h(A) = 1.
2.2 Unified Domain for Temporal Data
In the introduction we have seen that, in classical
TDB, the valid time is managed thanks to the exten-
sion of the tables schemata by adding two new at-
tributtes (Clifford and Rao, 1987) (Elmasri and Wuu,
1990), the valid start time -VST- and the valid end
time -VET- to determine the period of validity of the
fact expressed by a tuple.
In this paper we are going to consider that the in-
formation provided by the VST and VET for the clas-
sical TDB is fuzzy, in the sense that we are not com-
pletely sure about when the current values of the tuple
began to be valid.
The more immediate solution to this problem is to
soften the VST and the VET in such a way that they
may contain fuzzy dates represented by means of a
fuzzy number. This means that, if we use the para-
metrical representation for fuzzy numbers, we need to
store four values for the VST and four values for the
VET, as shown in figure 4. Since the meaning of the
attributes VST and VET is the period of time during
which the values of a tuple are valid, it is more conve-
nient to summarize the information given by the two
fuzzy attributes in an only but fuzzy interval (from
now on FVP or fuzzy validity period). This situation
can be represented by the trapezoidal fuzzy set shown
in figure 5 which incorporates the semantics of our
problem. As can be seen in such figure, the left and
right sides of the interval is the part that reflects the
imprecision about the starting and ending time point
of the validity time of the facts associated.
9877
9877
BOSS
JUNIOR
TRAINEE
EXPERTISE
~ 31-05-1998~15-06-199715001245
GRANT
~undefined~01-06-199815001245
GRANT
VETVSTSALARYEMPIDEMPNAM
9877
9877
BOSS
JUNIOR
TRAINEE
EXPERTISE
~ 31-05-1998~15-06-199715001245
GRANT
~undefined~01-06-199815001245
GRANT
VETVSTSALARYEMPIDEMPNAM
(01-06-1998,01-06-1998,2,2)
(31-12-2050,31-12-2050,0,0)
Figure 4: Internal representation of a fuzzy date.
03/02/0831/01/08
1
04/03/0828/02/08
By February
Figure 5: Fuzzy Period of Time for a Valid Tuple.
This representation has the advantage that, not
only periods of time, but fuzzy dates can also be rep-
resented in a unified way. Think that a parametrical
representation as (m,m,a,b) represents a central time
point with some imprecision at both sides, what is in-
terpreted as a fuzzy date.
The problem now is that the imprecision provided
by the two fuzzy dates must be translated to the in-
terval that summarizes the considered period of time.
That is, all the imprecision of the starting date must
be converted in the imprecision of the left side of the
interval and, in the same way, all the imprecision of
the ending date must be converted in the imprecision
of the right side of the interval.
If we consider that a way to measure the impreci-
sion of a fuzzy set is to compute its area, the problem
we have in hands is a matter of geometrical computa-
tion.
TOWARDS A UNIFIED DOMAIN FOR FUZZY TEMPORAL DATABASES
357

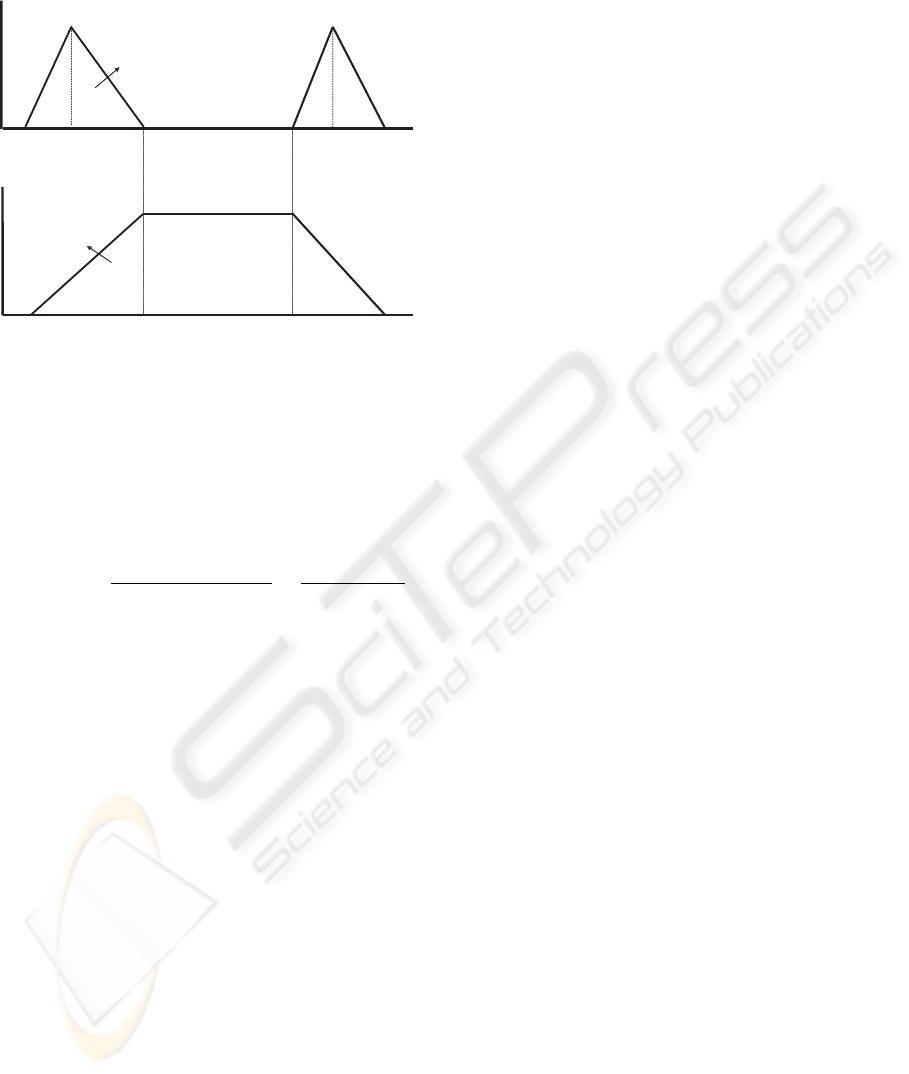
The posed problem is shown in a graphical way in
figure 6.
ds-as ds ds+bs de-ae de de+be
Starting Date Ending Date
Initial Data
d1-a d1 d2 d2+b
Transformed Data
S1
S2
Figure 6: Transformation of two fuzzy dates into a fuzzy
period preserving imprecision.
The resulting fuzzy interval is obtained by means
of the equality S
1
= S
2
that obliges to maintain the
same amount of imprecision after the transformation
is performed.
S
1
= S
2
=⇒
(d
s
+ b
s
) − (d
s
− a
s
)
2
=
d
1
− (d
1
− a)
2
If we assume that the data associated to this time
specification are precisely known from (d
s
+ b
s
) to
(d
e
− a
e
), then d
1
= d
s
+ b
s
and both terms become
equal and d
1
− a = d
s
− a
s
, as shown in figure 6. The
same substitution should be made to obtain the right
part of the interval.
As it was explained in section 1.2, it is quite easy
to represent a fuzzy interval with this characteristics
since only four parameters need to be stored in order
to specify it. In (Medina et al., 1994) (Medina et al.,
1995) is presented a generalized model of fuzzy DB
that supports this representation for fuzzy data and the
corresponding implementation in a classical relational
DB system (Oracle).
3 CONCLUSIONS AND FUTURE
WORK
In this paper we have shown how to represent differ-
ent time specifications in a unified way. The repre-
sentation considered is the fuzzy interval, which re-
sults very suitable for both precise and imprecise time
points and periods when the time is interpreted as
valid time. For the case that two fuzzy dates are pro-
vided by the user, it is necessary to perform a transfor-
mation to convert this original time information into a
fuzzy interval that preserves the imprecision involved.
ACKNOWLEDGEMENTS
This work has been partially supported by research
projects TIN2008-02066/TIC and P07-TIC-03175.
REFERENCES
Barro, S., Mar
´
ın, R., Mira, J., and Pat
´
on, A. R. (1994). A
model and a language for the fuzzy representation and
handling of time. Fuzzy Sets Syst., 61(2):153–175.
Bettini, C., Wang, X. S., and Jajodia, S. (1998). A general
framework for time granularity and its application to
temporal reasoning. Annals of Mathematics and Arti-
ficial Intelligence, 22(1-2):29–58.
Chountas, P. and Petrounias, I. (2000). Modelling and rep-
resentation of uncertain temporal information. Re-
quirements Eng., 5:144–156.
Clifford, J. and Rao, A. (1987). A simple, general structure
for temporal domains. In Temporal Aspects in Infor-
mation Systems, pages 17–28.
de Feri
´
et, J. K. (1973). La theorie generalise
´
ede
l’information et le mesure subjetive de l’information.
In de F
`
eriet, K. and Picard., C., editors, Lecture notes
in Math: Th
´
eories de l’information., volume 398,
pages 1–28. Springer-Verlag.
Dubois, D. and Prade, H. (1987). Fuzzy numbers: An
overview. In Bezdek, J., editor, Analysis of Fuzzy In-
formation, Vol.I: Mathematics and Logic, pages 3–39.
CRC Press, Boca Raton, FL.
Elmasri, R. and Wuu, G. T. J. (1990). A temporal model and
query language for er databases. In Proceedings of the
Sixth International Conference on Data Engineering,
pages 76–83, Washington, DC, USA. IEEE Computer
Society.
Goguen, J. (1967). L-fuzzy sets. Journ. of Math. Anal. and
Applications, 18:145–174.
Gonz
´
alez, A., Pons, O., and Vila, M. A. (1999). Dealing
with uncertainty and imprecision by means of fuzzy
numbers. Int. J. Approx. Reasoning, 21(3):233–256.
Medina, J. M., Pons, O., and Vila, M. A. (1994). Gefred: a
generalized model of fuzzy relational databases. Inf.
Sci. Inf. Comput. Sci., 76(1-2):87–109.
Medina, J. M., Vila, M. A., Cubero, J. C., and Pons, O.
(1995). Towards the implementation of a general-
ized fuzzy relational database model. Fuzzy Sets Syst.,
75(3):273–289.
Yager, R. (1981). Measurement of properties on fuzzy sets
and possibility distributions. In Klement, E., editor,
3rd Intern. Seminar on Fuzzy Set Theory, pages 211–
222. Johannes Keplas Univ. Liuz.
ICEIS 2009 - International Conference on Enterprise Information Systems
358