BUILDING TAILORED ONTOLOGIES FROM VERY LARGE

KNOWLEDGE RESOURCES

Victoria Nebot and Rafael Berlanga

Departamento de Lenguajes y Sistemas Inform´aticos, Universitat Jaume I

Campus de Riu Sec, 12071, Castell´on, Spain

Keywords:

Ontology generation, Ontology indexing, Knowledge repositories.

Abstract:

Nowadays very large domain knowledge resources are being developed in domains like Biomedicine. Users

and applications can beneﬁt enormously from these repositories in very different tasks, such as visualization,

vocabulary homogenizing and classiﬁcation. However, due to their large size and lack of formal semantics,

they cannot be properly managed and exploited. Instead, it is necessary to provide small and useful logic-

based ontologies from these large knowledge resource so that they become manageable and the user can take

beneﬁt from the semantics encoded. In this work we present a novel framework for efﬁciently indexing and

generating ontologies according to the user requirements. Moreover, the generated ontologies are encoded

using OWL logic-based axioms so that ontologies are provided with reasoning capabilities. Such a framework

relies on an interval labeling scheme that efﬁciently manages the transitive relationships present in the domain

knowledge resources. We have evaluated the proposed framework over the Uniﬁed Medical Language System

(UMLS). Results show very good performance and scalability, demonstrating the applicability of the proposed

framework in real scenarios.

1 INTRODUCTION

Ontologies are a knowledge representation formalism

that capture the semantics of the real world entities

by deﬁning concepts and the relationships between

them. The knowledge captured in ontologies can be

used, among other things, to share common under-

standing of the structure of information among people

and/or software agents, to enable the reuse of domain

knowledge and to introduce standards to allow inter-

operability (Noy et al., 2001). Recently, many ap-

plication domains are being represented using ontolo-

gies, one of the most prominent being the life-science

ﬁelds. An example of a large repository of biomedi-

cal information is the Uniﬁed Medical Language Sys-

tem (UMLS). This knowledge resource is a vast and

very comprehensive repository of information. How-

ever, the large amount of different terminologies it

gathers makes it hard to select a relevant and man-

ageable subset for an speciﬁc application. Moreover,

UMLS is not represented in a standard interchange

ontology language such as the W3C recommended

OWL, which prevents the knowledge base from the

beneﬁts of logic-based formalisms.

In this paper, we tackle the evident scaling prob-

lems when dealing with very large and complex

knowledge resources. Our proposal consists of

a framework for building compact and customized

logic-based ontologies from large knowledge re-

sources. The proposed system allows the user to spec-

ify a query as free-text, which encapsulates the se-

mantics the output ontology should gather. The input

query goes through a process of semantic annotation

and later assessment in order to obtain a set of rel-

evant and meaningful ontology concepts. These set

of concepts, called signature, is used by the Ontology

Extractor to obtain a speciﬁc application-oriented on-

tology in OWL format. To our best knowledge, our

approach is the ﬁrst one on addressing the following

requirements:

• Scalability. Knowledge resources tend to be

large and complex repositories of information.

We achieve scalability through the use of tools

aimed at extracting customized ontologies from

the knowledge resources, which just involve the

necessary elements.

• Ontology Compactness. Speciﬁc application

ontologies are usually subject-oriented, which

means they gather semantically related concepts.

The compactness of these ontologies depends

greatly on the precision of the semantic annota-

144

Nebot V. and Berlanga R. (2009).

BUILDING TAILORED ONTOLOGIES FROM VERY LARGE KNOWLEDGE RESOURCES.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

144-151

DOI: 10.5220/0001984001440151

 SciTePress

tion of the user query. Therefore, we propose an

assessment step that ﬁlters the semantic annota-

tions obtained based on the conceptual density of

each selected ontology concept.

• Logic-based Formalism. The ontologies built

from the knowledge resources are represented in

OWL, which offers several advantages such as

reasoning capabilities, consistency of terminol-

ogy, sharing and reusing knowledge, etc.

The rest of the paper is organized as follows. Sec-

tion 2 describes an application scenario that motivates

the proposed approach of building OWL ontologies

from large knowledgeresources. Section 3 explainsin

detail the different components of the framework and

Section 4 shows the evaluation performed. Finally,

Section 5 gives some conclusions and future work.

2 APPLICATION SCENARIO

In the biomedical domain, the gathering and repre-

sentation of knowledge have been the main concerns

of researchers and domain experts for several years.

Supporting evidence is the great effort made by the

National Library of Medicine (US) in developing the

UMLS over the past 18 years. UMLS can be thought

as a large repository of biological and clinical infor-

mation covering multiple domains: from genetics and

celular to disease level. The version 2007AC has

1,516,299 concepts and 13,226,382 relations. UMLS

includes three resources: the Metathesaurus, the Se-

mantic Network, and the Specialist Lexicon. The ﬁrst

one consists of several thesauri (more than 100 differ-

ent sources such as FMA, MeSH, etc.) The Seman-

tic Network consists of 135 semantic types organised

in 7 main groups - e.g. anatomical structure or bi-

ologic function - and linked by “is

a” relationships.

There are also 53 kind of non-hierarchical relation-

ships among these semantic types, e.g. causes(Virus,

Disease). A concept of the metathesaurus can be as-

signed at one or more semantic types in the Semantic

Network. The SPECIALIST Lexicon, the third re-

source of UMLS, has been developed in order to pro-

vide lexical information needed for an NLP applica-

tion e.g. syntactic, morphological. It includes many

biomedical terms, dictionaries of abbreviations, etc.

The conceptual model of UMLS is centred on

Sources (i.e. ICD-10, MesH), which contain Atoms

(the distinct concepts within each source). Each Atom

is assigned to one and only one Concept, whose iden-

tiﬁer is called CUI. Concepts consist in Terms ow-

ing the same meaning. One Term can belong to sev-

eral concepts but not often. Terms consist of Strings,

i.e. string variants. Figure 1 shows an example of

the conceptual model of UMLS. The proposed frame-

work works at the level of concept identiﬁers (CUIs).

Figure 1: Conceptual model of UMLS.

UMLS can be considered a vast and complex on-

tology, from which is hard to select a relevant man-

ageable subset for a speciﬁc application. Moreover,

the metathesaurus gathers vocabularies that have been

developed independently, resulting in a lot of incon-

sistencies such as cycles in hierarchies. Moreover,

the UMLS knowledge resource has a proprietary for-

mat, which prevents interoperability and the use of

standard languages and tools designed for the Seman-

tic Web. One could think of translating the whole

metathesaurus into OWL. However, authors such as

(Cornet and Abu-Hanna, 2002) and (Kashyap and

Borgida, 2003) claim this is not feasible since the se-

mantics of the relations present in the vocabularies

(e.g. ICD, MeSH) is often underspeciﬁed. Therefore,

UMLS relations can be interpreted in several ways.

As a result, only the Semantic Network has been

translated into OWL (Kashyap and Borgida, 2003).

Our proposal addresses this issue by building speciﬁc

ontologies tailored to the needs of a concrete applica-

tion. The output ontology should be used by knowing

that it is a speciﬁc interpretation of the metathesaurus.

Moreover, we put special emphasis in building on-

tologies in a logic-based formalism such as OWL due

to the several advantages it offers. OWL brings pow-

erful reasoning based on Description Logic (DL). In

the biomedical domain, reasoning can be a very pow-

erful tool to infer new or implicit knowledge. For ex-

ample, it can serve to make relevant links between two

different biomedical domains. Moreover, we can also

check the consistency of the terminology and perform

more meaningful queries. On the other hand, adding

a description logic to a large coarse-grained concep-

tual model of a biomedical domain serves to disam-

biguate imprecise representations. Finally, by using

OWL, which is a W3C standard, we can beneﬁt from

the tools made available for OWL as well as share and

reuse knowledge in an easy way.

BUILDING TAILORED ONTOLOGIES FROM VERY LARGE KNOWLEDGE RESOURCES

145

3 SYSTEM ARCHITECTURE

In this section we present the framework for building

tailored application ontologies from very large knowl-

edge resources. Figure 2 shows the different compo-

nents of the framework. The workﬂow of the frame-

work is as follows: the user speciﬁes a free-text query

that describes the application ontology he wants to

obtain. The Symbol Searcher tool performs the Se-

mantic Annotation of the user query with the lexicon

of the knowledge resource. The set of obtained con-

cepts go through an Assessment step that ﬁlters the

concepts according to their conceptual density. The

output of the Symbol Searcher tool is the signature,

which is composed by the knowledge resource con-

cepts that best match the user query both syntacti-

cally and semantically. Taking as input the signature,

the Ontology Extractor retrieves from the knowledge

resource the sub-ontology (necessary concepts along

with their taxonomic relationships) that best covers

the signature. In a ﬁnal step, the ontology is converted

into OWL format and further enriched with additional

OWL axioms.

Figure 2: Framework for building logic based application

ontologies from knowledge resources.

Next sections are devoted to explain with more de-

tail the main components of the framework, which are

in turn the Symbol Searcher, Ontology Extractor and

OWL Converter.

3.1 Symbol Searcher

The Symbol Searcher is in charge of ﬁnding the ap-

propriate set of ontology concepts that best match the

user query. This process is carried out in two phases,

which will be explained in turn: Semantic Annotation

and Assessment.

3.1.1 Semantic Annotation

The main idea behind semantic annotation is the iden-

tiﬁcation of relevant terms and the linking of these

terms to thesauri, databases or ontologies. In our ap-

plication scenario, we are interested in ﬁnding rel-

evant terms in the user query and linking them to

UMLS concepts. One option consists of performing

manual annotation. However, this process is subject

to human errors and factors such as familiarity with

the domain, scale of the knowledge resource, etc. An

alternative to overcome these difﬁculties is the auto-

matic semantic annotation of text. MetaMap (Aron-

son, 2001) and Whatizit (Rebholz-Schuhmann et al.,

2007) are examples of automatic semantic annotators

that use large terminological databases as input lexi-

cons. MetaMap has been speciﬁcally designed to map

text into concepts from the UMLS Metathesaurus

while Whatizit can be used on several resources such

as UniProtKb/Swiss-Prot, GO, UMLS, etc. Both se-

mantic annotators have been tested in the context of

the application scenario and, although they are effec-

tive, a supervised process is still required to complete

and verify the obtained annotations. Since we want all

the steps of the framework to be as automatic as pos-

sible, in the next section we propose an assessment

step that ﬁlters out the concepts found by the seman-

tic annotator.

3.1.2 Assessment

The quality and compactness of the resulting applica-

tion ontology is severely affected by the input signa-

ture used to generate it. As earlier mentioned, auto-

matic semantic annotators are subject to imprecission

and ambiguity. Therefore, the objectiveof this assess-

ment step is to evaluate and rank the output ontology

concepts found by the semantic annotator according

to their conceptual density. Let C be the set of con-

cepts found by the semantic annotator and N its size.

We deﬁne the conceptual density of a concept of C as

follows:

CD(c) =

∑

∈C,c

6=c

d(c,c

)

(1)

where d(c, c

) is the taxonomic distance between con-

cepts c and c

in the knowledge resource.

Notice that CD(c) = 1 if the rest of concepts from

C are direct neighbours of c. Therefore, concepts with

biggerCD are closer one another in the knowledge re-

source, while concepts with smaller CD are far away

from the rest of concepts in C. The latter probably

correspond to incorrect or ambiguous semantic anno-

tations. In order to ﬁlter them out the user can specify

ICEIS 2009 - International Conference on Enterprise Information Systems

146

a minimum Threshold as shown in Figure 2. With this

procedure we remove concepts found by the seman-

tic annotator that may introduce noise in the resulting

ontology.

3.2 Ontology Extractor

The Ontology Extractor task consists of retrieving

from the knowledge resource an application ontology

(e.g. a set of concepts along with their taxonomic re-

lationships) that fulﬁls the user needs. The applica-

tion ontology has to provide the necessary semantics

demanded by the user query while keeping a reduced

size in order to achieve scalability. In order to ac-

complish both requirements we have developed and

tested an indexing mechanism over the “is-a” rela-

tionships of the knowledge resource that enables us to

efﬁciently retrieve a small subset that satisﬁes the user

query. Next section describes the indexing process of

the knowledge resource and then we present an ontol-

ogy retrieval strategy based on the indexes created.

3.2.1 Knowledge Resource Indexing Process

In most knowledge resources, as is the case of UMLS,

concepts are organized into “is-a” hierarchies, which

constitute the backbone of the repository. This leads

to an underlying graph-like structure. In order to efﬁ-

ciently retrieve a sub-ontology from this graph struc-

ture guided by the signature, we need some kind of

indexing scheme over the graph that encodes descen-

dant and ancestor relationships in a compressed and

efﬁcient way. We have adopted a labeling scheme,

which assigns to each node in the graph some iden-

tiﬁer that allows the computation of relationships

between nodes using simple arithmetic operations.

For our purposes, we have adopted and extended

Agrawal’s interval scheme (Agrawal et al., 1989) but

with a labeling variation from (Schubert et al., 1983),

which takes preorder identiﬁers of nodes instead of

postorders used in Agrawal’s technique. The ap-

proach can be applied to directed trees and Directed

Acyclic Graphs (DAGs), which will be the underly-

ing structure of most ontologies (Christophides et al.,

2003). With respect to our application scenario, we

have preprocessed UMLS in order to delete cycles in

the “is-a” hierarchy and obtain a DAG.

Figure 3 (left graph) shows a labeled DAG. The

process is as follows: in an initial step, disjoint com-

ponents can be hooked together by creating a virtual

root node. The compression scheme ﬁrst ﬁnds a span-

ning tree T for the given graph (solid edges). Then it

assigns an interval to each node based on the preorder

traversal of T. That is, the interval associated with a

node v is [pre(v), maxpre(v)], where pre(v) is the pre-

order number of v and maxpre(v) is the highest pre-

order number of v’s descendants. Notice the preorder

of each node is used as its unique identiﬁer. Next, all

nodes of the graph are examined in the reverse topo-

logical order so that for every edge from node p to

q, all the intervals associated with node q are added

to the intervals associated with node p, taking into

account that if one interval is subsumed by another,

the subsumed interval is not added. In the ﬁgure, the

interval [2, 7] is associated to node d when labeling

the spanning tree. Then, during the reverse topologi-

cal traversal, node d inherits intervals [6, 6], [4, 6] and

[5, 5] corresponding to nodes g, e and h, which come

from the dashed edges not belonging to the spanning

tree. Since these intervals are already subsumed by

d’s interval [2,7], they are not added to d. Otherwise,

they would be included.

The storage requirements for trees labeled with

this interval scheme is O(n), since one interval per

node is enough. For DAGs, the worst case requires

O(n

) space. However, this situation is unlikely be-

cause Agrawal’s approach for DAGs ﬁnds the opti-

mum spanning tree, that is, the spanning tree that

leads to minimum amount of intervals per node and

thus, minimum storage requirements.

Next step consists of obtaining analogous infor-

mation about ancestors of each node. The strategy ap-

plied is as follows. First, we reverse the edges of the

original structure so that each node now points to its

parent/s (see right graph of Figure 3). Then, a virtual

root node has to be created to hook together what are

leaf nodes in the original structure. Then, the same la-

beling scheme described previously is applied to the

reversed structure. Since now the edges denote an-

cestor relationships, the labeling scheme will encode

ancestor nodes. Notice that each node identiﬁer is its

preorder number and both the original structure and

the reversed one have each own preorder system.

We ﬁnally deﬁne the descriptor function of a node

v as follows:

descriptor(v) =<descpre(v), descintervals(v),

ancpre(v), ancintervals(v),

topo(v) >

where descpre(v) denotes the preorder number of v in

the original structure, descintervals(v) denotes the set

of intervals encoding v’s descendants, ancpre(v) de-

notes the preorder number of v in the reversed struc-

ture, ancintervals(v) denotes the set of intervals en-

coding v’s ancestors and topo(v) denotes the topolog-

ical order of v.

Gathering all together, we have designed an en-

coding mechanism for concepts in a knowledge re-

BUILDING TAILORED ONTOLOGIES FROM VERY LARGE KNOWLEDGE RESOURCES

147

Figure 3: Compressed transitive closure of descendants (left graph) and ancestors (right graph).

source based on interval labeling schemes that is able

to encapsulate in a compressed and efﬁcient way all

the descendants and ancestors of each concept. The

information encapsulated in the concept descriptors

can be exploited to efﬁciently retrieve related con-

cepts. Therefore, we deﬁne a set of operations in-

tended to manipulate the intervals of the descriptors.

The most important operations are the next:

• The descendants of v is the serialization of

descintervals(v).

• The ancestors of v is the serialization of

ancintervals(v).

• The topological order of v is topo(v).

• Concept v

subsumes v

if:

descintervals(v

) ∩ descintervals(v

) ==

descintervals(v

)

• Common ancestors of v

and v

are:

ancintervals(v

) ∩ ancintervals(v

• Nearest common ancestor of v

and v

is:

max{topo(commonAncestors(v

, v

))}.

3.2.2 Ontology Retrieval Strategy

The aim of the strategy presented in this section is to

extract ontologies with a reduced size and relevant to

the user query. The output constitutes the skeleton

of the application ontology (“is-a” relationships with

tree-like structure). This ontology skeleton can be

further enriched with additional “is-a” relationships

in order to obtain a DAG structure, which has the

property of preserving all the taxonomic relationships

among the input signature concepts. This section is

dedicated to describe the strategy followed in order

to achieve such a goal.

Algorithm 1: Compute spanning tree.

Require: L list of output nodes sorted by preorder number

Ensure: G spanning tree of the output nodes

Stack parents =

C = next node(L)

D = next node(L)

while L do

if subsumes(descintervals(C), descintervals(D) then

add edge(G, edge(C, D))

push(parents, D)

C = D

D = next node(L)

else

pop(parents)

C = top(parents)

end if

end while

All Signature Ancestors (ASA). The ontology re-

trieval strategy presented consists of extracting all an-

cestors from the signature concepts encoded in the de-

scriptors. Then, Algorithm 1 computes a spanning

tree with the signature and their ancestors based on

their subsumption relationships encoded in the de-

scendant intervals. The output ontology contains all

concepts from the signature plus all their ancestors

organized by their “is-a” relationships.

Figure 4 shows an example of the output ontolo-

gies (tree-like structure) that would be retrieved by

this strategy and the reﬁnement presented next tak-

ing as starting point the same signature. Figure 4.a

shows the underlying graph-like “is-a” relationships

of the original knowledge resource, in which thicker

lines correspond to the spanning tree calculated by the

interval labeling scheme described in Section 3.2.1.

Figure 4.b including the crossed out nodes corre-

sponds to the ontology skeleton that would be re-

trieved by ASA strategy, in which black nodes are the

input signature.

ICEIS 2009 - International Conference on Enterprise Information Systems

148

Figure 4: Output ontology skeleton. a) Original knowledge

resource “is-a” relationships; b) Output ontology of ASA

(all nodes) and ASA-ST (crossed out nodes not included).

Algorithm 2: Search additional edges to get a DAG.

Require: G output tree structure of ASA or ASA-ST

Ensure: G with DAG-structure

sorted nodes = topological order(G)

for all node n in sorted nodes do

ancestors = ancestors(n)

while ancestors do

nearest ancestor =

get nearest ancestor(n, ancestors)

add edge(G, edge(nearest ancestor, n)

nodes to root =

get nodes to root(nearest ancestor)

delete from(ancestors, nodes to root)

end while

end for

All Signature Ancestors Spanning Tree (ASA-ST).

In the previous approach, retrieving all ancestors

from the signature concepts can result in an excessive

amount of nodes in the output ontology that are not

relevant to the reconstructed hierarchy. Thus, we

have introduced an enhancement by just selecting

ancestor nodes that relate concepts of the signature

through the spanning tree calculated (see crossed

out nodes of Figure 4.b). This approach can be

considered an extension of ASA strategy, since it is

applied to the ASA output ontology. In this strategy,

deleted nodes do not participate in the transitive

closure of the signature, thus, it is not altered. The

experiments performed show that ASA-ST strategy

is more adequate when working with UMLS due

the great amount of unrelevant ancestors pruned.

Therefore, we take ASA-ST strategy as the one

suitable for our application scenario.

Obtaining a DAG. The output ontology consists of a

tree structure for simplicity, since many applications

do not require all “is-a” relationships among concepts

but rather a tree hierarchy (e.g. datawarehouse dimen-

sions). However, in many cases it is necessary to get

the complete DAG structure. For this purpose, the Al-

gorithm 2 has been designed.

This algorithm adds the remaining relationships

between pairs of nodes belonging to the signature.

This is accomplished by calculating nearest ancestors

using the topological order of nodes.

This algorithm does not add an extra temporal

complexity because all operations have a linear cost

w.r.t. the number of nodes if they make use of the

descriptor functions of each node.

3.2.3 UMLS Speciﬁc Customizations

The indexing scheme and ontology retrieval strategy

presented in this paper are not speciﬁc to UMLS.

They can be applied to any knowledge resource with

some kind of transitiverelationship (e.g. “is-a”, “part-

of”, etc.). However, once the ontology skeleton is ob-

tained one can enrich it with speciﬁc features from the

knowledge resource. In the case of UMLS, concepts

belong to one or more semantic types as explained

in Section 2. Therefore, we enrich the graph structure

obtained in the previous phase with the corresponding

semantic types and “is-a” relationships.

3.3 OWL Converter

The ﬁnal step performed by the system consists of

building an interchangeable OWL ﬁle with the graph-

based structure returned by the Ontology Extractor.

Table 1 summarizes the patterns applied to the graph

to obtain the ﬁnal OWL ontology. For the sake of

space, we use DL notation instead of OWL construc-

tors. Axiom 1 converts a node, which represents a

concept, into an OWL class. Then, axiom 2 adds a

subClassOf axiom for each edge, which represents an

“is-a” relationship. By applying the previous axioms

we obtain a taxonomy where classes are primitive, i.e.

without explicit deﬁnition. In order to enrich the on-

tology with reasoning capabilities, we need to make

explicit some concept deﬁnitions using existing ones.

Axioms 3 and 4 performthis task. In particular,axiom

3 deﬁnes a concept as the intersection of its parents,

while axiom 4 deﬁnes a concept as the union of its

children. Additionally, axiom 5 includes UMLS re-

lationships as ObjectProperties and Restrictions over

the involved concepts only if both domain and range

are included in the graph so that we obtain closed on-

tologies. Following (Kashyap and Borgida, 2003), we

only add axiom 5 if the corresponding relationship is

not blocked in the Semantic Network. Finally, we can

further enrich the ontology concepts and properties

with annotations provided by the knowledge resource

(e.g. label, comment, user-deﬁned annotation proper-

ties, etc).

BUILDING TAILORED ONTOLOGIES FROM VERY LARGE KNOWLEDGE RESOURCES

149

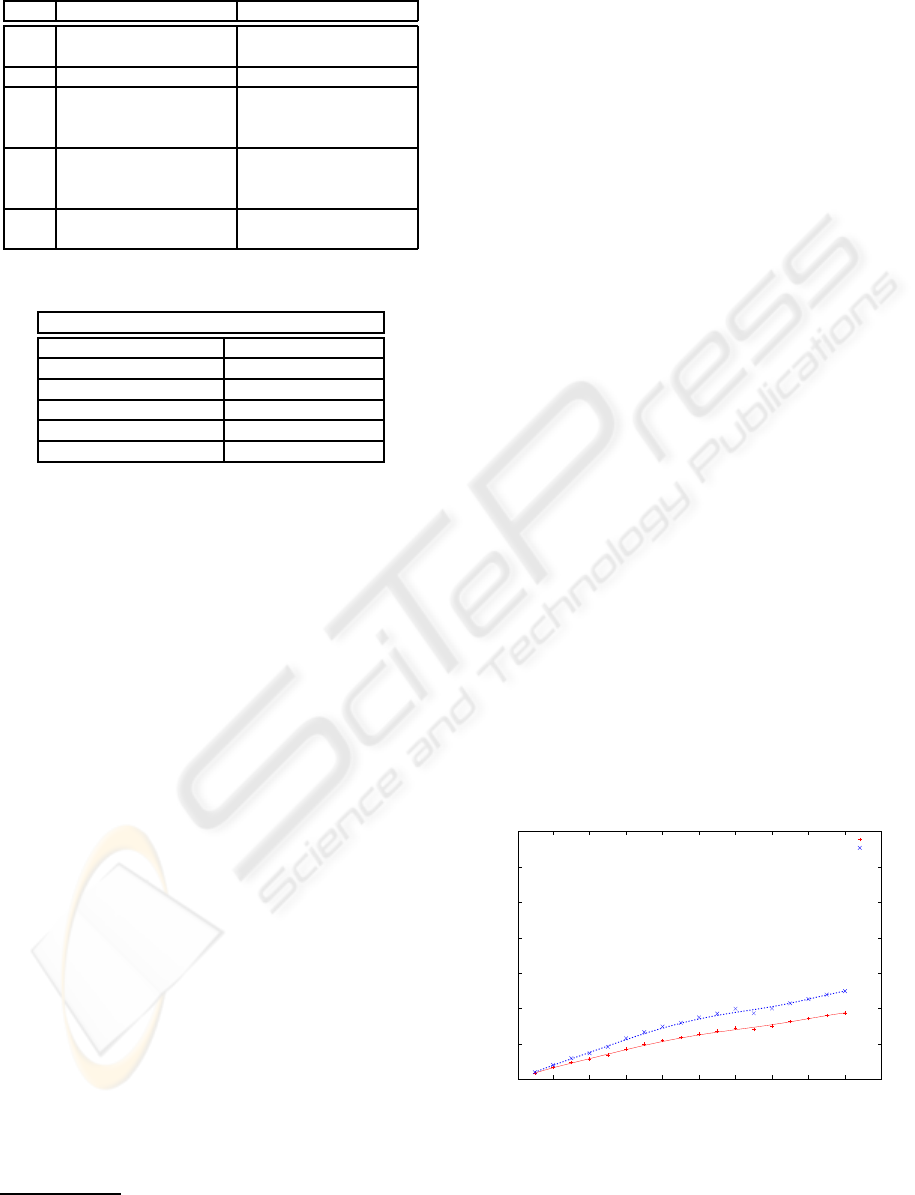
Table 1: OWL conversions from a DAG structure.

DAG OWL (DL)

(1) node(C) C

C ∈ CUIs∪Semtypes

(2) edge(D,C) C ⊑ D

(3) edge(D

,C)

. . . C ⊑ (≡)D

⊓ . . . ⊓ D

edge(D

,C)

(4) edge(C, D

)

. . . C ≡ D

⊔ . . . ⊔ D

edge(C, D

)

(5) node(A), node(C) A ⊑ ∃R.C

R(A,C)

Table 2: UMLS statistics: # intervals per descriptor.

UMLS number of intervals per descriptor

Number of descriptors 293041

Avg. descendants 2.28

Max. descendants 2326

Avg. ancestors 11.46

Max. ancestors 114

Depth 27

4 EVALUATION

In the following, we describe the experiments per-

formed over the UMLS to prove that our framework

is both scalable and able to retrieve relatively small

sized ontologies compared to the whole knowledge

resource. A prototype was implemented in Python

and MySql has been used as back-end storage system

for the indexes.

Firstly, Table 2 shows some statistics about the

size of the indexes generated by our ontology index-

ing system (concept descriptors) for UMLS. As we

can observe, the maximum number of intervals in a

concept descriptor can be quite large but this is not

usual at all since the average in the descendant inter-

vals is really low while in the ancestors’ increases but

not too much. Thus, we can state that our indexes

are scalable when dealing with large knowledge re-

sources. Some of these repositories have a high de-

gree of dynamism, since they are continously evolv-

ing and growing(e.g. a new version of UMLS is made

available every few months, more or less). This is not

quite a problem for our framework since newer ver-

sions of repositories can be indexed in a few minutes.

The performance evaluation of the framework has

been carried out over a set of 100 different signatures

derived from a collection of 15000 abstracts taken

from MEDLINE. These signatures have been devel-

oped in the context of the Health-e-Child

project,

Health-e-Child Project: http://www.health-e-child.org

where each signature represents a different perspec-

tive for the study of a given disease. We selected

the diseases Juvenile Idiopathic Arthritis (JIA) and

Tetralogy of Fallot (TOF). Abstracts are processed

with a semantic tagger, in our case (Jimeno et al.,

2008), which identiﬁes UMLS concepts from texts.

These concepts are grouped according to the target

disease (JIA or TOF) and their semantic type. For

the assesment phase, the conceptual density has been

shown quite useful to detect both wrongly annotated

strings and non-relevant concepts derived from the

user’s request. In the experiments, we have com-

bined the conceptual density with the frequency in

which concept strings occur in the collection. In this

way, concepts with high frequency and low density

are likely to be wrong annotations, whereas concepts

with low frequency and relative low density are not

relevant to the signature. In both cases, concepts are

removed from the signature. Notice that this reduc-

tion contributes to the increase of both the compact-

ness and the performance of the ontology construction

process. In our experiments the density threshold is

around 0.1, under which concepts can be potentially

rejected. The resulting groups constitute the signa-

tures for the experiments.

Figure 5 shows the size of the output ontology as

the size of the signature increases for both versions

of strategy ASA-ST (tree and DAG). The size of the

ontology (axis Y) is measured in number of edges

since both versions extract an ontology with the same

amount of nodes. The increase of edges in the DAG

version is due to the fact that UMLS mixes different

classiﬁcations over the same concepts, and this leads

to multiple inheritance. Overall, we can predict a lin-

ear tendency of the ontology size as the signature in-

creases in both versions.

200

400

600

800

1000

1200

1400

20 40 60 80 100 120 140 160 180 200

# of edges

signature’s size

Increase of edges from spanning tree to DAG with ASA-ST

spanning tree

DAG

Figure 5: Signature’s size vs. ontology’s size.

We have also evaluated the temporal complexity

of both ASA-ST versions (see Figure 6). Although

ICEIS 2009 - International Conference on Enterprise Information Systems

150

the time required to generate a DAG is slightly larger,

the general tendency is linear in both cases.

0 20 40 60 80 100 120 140 160 180

time (s)

signature’s size

Signature’s size vs. time

ASA-ST (tree)

ASA-ST (DAG)

Figure 6: Signature’s size vs. temporal complexity.

5 CONCLUSIONS

Using semantics and managing efﬁciently very large

domain knowledge resources suffers severely from

scaling problems. The framework presented in this

paper is a way of overcoming these difﬁculties. De-

velopers can use it to quickly create an application

logic-based ontology that covers just a small part of

the knowledge resource. Moreover, ontologies gener-

ated and enriched with a DAG-structure preserve the

taxonomic relationships over the signature concepts.

Evaluation has shown ontologies generated with

this framework keep their size relatively small and

manageable according to their signature. There-

fore, the framework presented achieves scalability by

providing compact and logic-based OWL ontologies

from very large knowledge resources.

In the future, we plan to study different relevance

judgements for the assessment phase that help ﬁlter-

ing out semantic annotations. We are also interested

in ﬁnding an automatic method for the calculation of a

threshold in this phase. Other future lines focus more

on the relationships of the knowledge resource and in

ﬁnding efﬁcient indexing techniques that allow to ef-

ﬁciently manage them.

REFERENCES

Agrawal, R., Borgida, A., and Jagadish, H. V. (1989). Ef-

ﬁcient management of transitive relationships in large

data and knowledge bases. In SIGMOD ’89: Proceed-

ings of the 1989 ACM SIGMOD international confer-

ence on Management of data, pages 253–262, New

York, NY, USA. ACM.

Aronson, A. R. (2001). Effective mapping of biomedical

text to the UMLS metathesaurus: the metamap pro-

gram. Proc AMIA Symp, pages 17–21.

Christophides, V., Plexousakis, D., Scholl, M., and Tourtou-

nis, S. (2003). On labeling schemes for the semantic

web. In WWW, pages 544–555.

Cornet, R. and Abu-Hanna, A. (2002). Usability of expres-

sive description logics – a case study in UMLS. In

Proc. AMIA Symp, pages 180–4.

Jimeno, A., Jimenez-Ruiz, E., Lee, V., Gaudan, S.,

Berlanga, R., and Rebholz-Schuhmann, D. (2008).

Assessment of disease named entity recognition on a

corpus of annotated sentences. BMC Bioinformatics,

9(Suppl 3):S3.

Kashyap, V. and Borgida, A. (2003). Representing the

UMLS semantic network using owl: (or ”what’s in a

semantic web link?”). In Fensel, D., Sycara, K. P., and

Mylopoulos, J., editors, International Semantic Web

Conference, volume 2870 of Lecture Notes in Com-

puter Science, pages 1–16. Springer.

Noy, N. F., Sintek, M., Decker, S., Crub´ezy, M., Fergerson,

R. W., and Musen, M. A. (2001). Creating seman-

tic web contents with prot´eg´e-2000. IEEE Intelligent

Systems, 16(2):60–71.

Rebholz-Schuhmann, D., Arregui, M., Gaudan, S., Kirsch,

H., and Yepes, A. J. (2007). Text processing through

web services: Calling whatizit. Bioinformatics, pages

btm557+.

Schubert, L. K., Papalaskaris, M. A., and Taugher, J.

(1983). Determining type, part, color and time rela-

tionships. IEEE Computer, 16(10):53–60.

BUILDING TAILORED ONTOLOGIES FROM VERY LARGE KNOWLEDGE RESOURCES

151