AN USER-CENTRIC AND SEMANTIC-DRIVEN QUERY

REWRITING OVER PROTEOMICS XML SOURCES

Kunalè Kudagba, Omar El Beqqali

MISI Research Group, USMBA University, Dhar El Mehraz Faculty of sciences, Fes, Morocco

Hassan Badir

SIC Department, National School of Applied Science (ENSA), Tangier, Morocco

Keywords: Proteomics, Ontology, XML, Trees, Semantic Web, Query Rewriting, Minimal Transversals.

Abstract: Querying and sharing Web proteomics data is not an easy task. Given that, several data sources can be used

to answer the same sub-goals in the Global query, it is obvious that we can have many candidates

rewritings. The user-query is formulated using Concepts and Properties related to Proteomics research

(Domain Ontology). Semantic mappings describe the contents of underlying sources. In this paper, we

propose a characterization of query rewriting problem using semantic mappings as an associated

hypergraph. Hence, the generation of candidates’ rewritings can be formulated as the discovery of minimal

Transversals of an hypergraph. We exploit and adapt algorithms available in Hypergraph Theory to find all

candidates rewritings from a query answering problem. Then, in future work, some relevant criteria could

help to determine optimal and qualitative rewritings, according to user needs, and sources performances.

1 INTRODUCTION

The rapid progress of biotechnologies and the

multiple genome project (Davidson, 1995) (Bishop,

1999) about organisms and diverse species have

generated an increasing amount of proteomic data

stored in many sources (Kohler, 2004), available and

publicly accessible on the Web. They contain data

about metabolic pathways, protein 3D structures,

DNA Sequences, organisms, diseases, and so on.

Many biological questions require that data from

several data sources are queried, searched, and

integrated. The first step in this process of Data

Integration is the Query rewriting which consists of

reformulating a global query in several specific local

queries. The query rewriting problem has recently

received significant attention because of its

relevance to a wide variety of data management

problems (Halevy, 2001): query optimization,

maintenance of physical data independence, data

integration, and data warehouse design.

Semantic mappings can be used to adapt a

global query expressed in terms of a Domain

Ontology in terms of specific local sources. In fact,

as several sources could provide expected resources,

more than one could be relevant to rewrite the global

query.

The motivation of this work is to investigate how

to generate candidate rewritings when user-query is

posed over XML Sources, and mappings are

expressed in LAV Approach. To achieve this goal,

we characterize the query rewriting problem as

minimal Transversals Discovery from an associated

Hypergraph. From this set of generated rewritings,

we would compute an optimal and best quality

rewriting based on some defined and relevant

criteria. We illustrate an intuitive execution of the

rewriting algorithm proposed, using a scenario of

Proteomics data sources.

The following two XML sources contain data

that are semantically similar, but are described with

autonomous and heterogeneous schemas. They both

represent the same proteomics data, but not

identically. They give an idea of differences in terms

of terminologies, structures and contents.

123

Kudagba K., El Beqqali O. and Badir H. (2009).

AN USER-CENTRIC AND SEMANTIC-DRIVEN QUERY REWRITING OVER PROTEOMICS XML SOURCES .

In Proceedings of the 11th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages

123-130

DOI: 10.5220/0001986301230130

 SciTePress

 XML Data Source 1

 XML Data Source 2

We can remark also some semantics

heterogeneities, like ACC_NUMBER attribute in

Source 2 which is equivalent with ACCESSION

Element in Source 1.

Although both data sources contain semantically

similar proteomic data, the simple user query

”Which are proteins that are encoded by the gene

named by CSF2RB2 in Mus Musculus Organism? ”

need to be formulated quite differently with existing

XML query languages, like Xquery or XPath for

both sources.

So, flexible, user-centric and semantic

strategies of discovering relevant sources are needed

to compute optimal and best quality rewriting,

according to suitable criteria.

The rest of the paper is structured as follows.

Section 2 gives a brief survey on our related work

regarding existing query rewriting approach in

Mediators. Section 3 discusses the basic concept of

Knowledge representation. The hypergraph-based

semantic query rewriting algorithm is presented in

Section 4. The last section 5 draws the conclusions

and future work.

2 RELATED WORK

One of the first LAV systems that allow the

integration of XML is AGORA (Manolescu, 2001).

But AGORA still makes an extended use of the

relational model: Although it offers an XML view

for relational and XML data, this view is translated

into a generic relational schema, XML resources are

described as relational views over this schema and

XQuery expressions are translated to standard SQL

queries, which are then decomposed and evaluated.

Information Manifold (Levy, 1996) also follows

a local-as views approach. In this system, the global

schema is a flat relational schema, and Description

Logics are used to represent hierarchies of classes.

The sources are expressed as relational views over

this schema. Query rewriting is done by the Bucket

algorithm which rewrites a conjunctive query

expressed of the global schema using the source

views. It examines independently each of the query

sub-goals and tries to find rewritings but loses some

by considering the sub-goals in isolation.

STyX system (Fundulaki, 2002) already uses a

domain Ontology as global schema language and

translates an OQL-like global query language to

XQuery expressions on the heterogeneous XML

sources. STyX maps XPath expressions to ontology

concepts. (Amann, 2002) discuss a data integration

system whereby XML sources are mapped into a

simple ontology (supporting inheritance and roles,

but no description logic-style definitions).

In (Lehti, 2004) authors have also used to

integrate XML heterogeneous data sources. Their

work consists to map XML schema constructs to

concepts. The main difference to STyX is the

approach to semantic mapping. Although Lehti’s

approach is not as flexible and powerful as using

XPath mappings, it is in principle able to detect

inconsistencies in the mapping with the help of a

description logic reasoner (Baader¸ 2003).

Other data integration approaches that use an

Ontology as Global Schema, are either based on an

extended data warehouse. Semantic mediation in C-

Web (Baader¸ 2003) is based on thesauri. In Xyleme

mediator (Delobel, 2003), the global schema is a set

of abstracted DTDs which are terms Trees according

to domain vocabularies such as Culture or Tourism.

Both follow GLAV (GAV and LAV together)

because correspondences between Mediator

vocabulary and Sources vocabularies are expressed

by simpler path mappings.

Recently, with the development of Semantic

Web, mediation systems have been developed.

Project Piazza (Halevy, 2003) proposes an

<PROTEIN_SET>

<ENTRY_NAME>IL3B_MOUSE</ENTRY_NAME>

<PROTEIN_NAME>Interleukin-3 receptor

class II beta chain [Precursor]

</PROTEIN_NAME>

<GENE_NAME>CSF2RB2</GENE_NAME>

<ORGANISM taxonomy_id="10090">Mus

musculus</ORGANISM>

</PROTEIN>

…

</PROTEIN_SET>

<PROTEIN_BASE>

<ENTRY>IL3B_MOUSE</ENTRY>

<PROTEIN_NAME>Interleukin-3 receptor

class II beta chain [Precursor]

</PROTEIN_NAME>

<TAX_ID >10090</TAX_ID >

<NAME> Mus musculus</NAME>

</ORGANISM>

</PROTEIN>

….

</PROTEIN_BASE>

ICEIS 2009 - International Conference on Enterprise Information Systems

124

infrastructure based on Peer-to-Peer (like a

decentralized mediator) for RDF and OWL data

integration.

According to the query rewriting algorithm, you

can refer to (Halevy, 2001) for a large survey on the

Query rewriting problem. Our approach is inspired

by WS-CatalogNet’s semantic-driven Algorithm. In

this work, (Benatallah, 2006) have developed a

novel and more advanced query rewriting techniques

for flexible and effective E-Catalogs selection.

3 REPRESENTING

KNOWLEDGE

In order to rewrite semantically a global query, it is

essential to make a choice of an adequate abstraction

model for local sources and to express in a common

formalization language all available knowledge.

This last case concerns the domain ontology, the

semantic mappings, and the user query.

The proteomics sources which we are working

with are stored and available as XML Documents

according to their XML Schemas. XML (Bray,

1998) is presently becoming the standard for the

exchange of biological data sources. So, the reason

for the use of XML Sources for the data Integration

is obvious. XML Schemas (Thompson, 2000) are

more suitable than DTDs for expressing the syntax,

structural, cardinality and typing constraints required

by proteomics data. We propose to abstract sources

XML Schemas as unordered Trees, and we try to

propose a specification language based on

description logic (DL) (Baader, 2003) formalization

and reasoning (Trees Logics).

3.1 Trees Abstract Model

We know that XML Schemas are special XML

Documents. Various models have been proposed to

represent XML Documents. The W3C proposed a

generic model named Document Object Model

(DOM). In this model, presented in the current

section, XML Documents can be abstracted as

Trees. Our motivation using this way of abstraction

is to further exploit some achieved and well known

results on Trees Embedding Problem (Schielder,

2001) as knowledge semantic retrieval in an

integration framework.

3.2 Logic-based Trees Descriptions

To provide a semantic formalization, necessary for

rigorous characterisation of proteomic queries and

knowledges, we propose to use a description

language of hierarchic structures such as Trees,

based on Logics and called Trees-Logics.

Many researchers have addressed the question of

using logics over Trees. In (Deutsch, 2003 and

2005) authors have translated XQuery global queries

into local conjunctive queries over Trees in a Data

integration processes. In (Schielder, 2001) a

language called ApproXQL, which exploits among

others logical operators, to formalize more richer

and expressive requests, has been developed. These

requests expressed as conjunctive queries could be

illustrated and interpreted as Trees. Then, in the

paper (Gotlob and Koch, 2004) authors have studied

the complexity and the expressive power of

conjunctive queries over Trees.

So, we believe strongly that it is possible to

describe data Trees with a suitable subset of logical

formalisms (Baader, 2003). We want to exploit all

these works in order to provide a logical description

of hierarchical structures, such as Trees and

consequently Paths in particular. In our final

integration framework, both the phases of Trees

generation and their specification in Trees-Logics

are totally transparent for the user. We precise that

Description Logics (Baader, 2003) are a family of

logics which were developed for modeling complex

hierarchical structures and to provide a specialized

reasoning engine to do inferences on these

structures.

Due to the space limitation, we could not give

more details on Trees-Logics and so this paper will

focus only on the query rewriting problem.

4 QUERY REWRITING

In this section, we begin by presenting an abstraction

of our approach for query rewriting. Then, we show

that using some hypergraph Theory results can help

generate candidate rewritings. Therefore we present

the Classical algorithm to compute minimal

Transversals of a hypergraph. Finally, we illustrate

an execution of this alogorithm to find candidate

rewritings, given concrete case of bio-query

reformulation.

We recall that the main goal of query rewriting

phase is to reformulate a Global query

Q expressed

as Trees-Logics over Domain ontology, into Local

AN USER-CENTRIC AND SEMANTIC-DRIVEN QUERY REWRITING OVER PROTEOMICS XML SOURCES

125

queries

that are expressed in terms of Local

schemas. This operation is realized using semantic

mappings pre-calculated and stored on the mediator.

Semi-automatic detection of semantic mappings has

no impact on the processing time of the user query.

The concrete algorithm showing how these semantic

mappings are calculated is out of scope of this paper.

The domain Ontology is abstracted as a Tree and

expressed using the defined language, Trees-Logics.

The knowledge domain concerns proteomics

research including concepts such Protein Family, 3D

Structures, Coding Genes, Motifs, Domains, amino-

acids sequences, Active Sites, Binding Sites,

Enzymes, Chains, Chemical Bonds, … and their

relative properties, so we call the ontology by

O’proteomics. Due to space constraints, we could

not give more details on O’proteomics.

The Ontology constitutes a support for user

query formulation and gives an idea of which

concepts, it is possible (but not obliged) to find or

retrieve in the underlying Proteomics sources.

Therefore, the first initiative consists of determining

the part of the query that cannot be answered by

available proteomics sources.

4.1 Query Rewriting Formalization

We represent by the following couple

),'(' mappingsMproteomicsOOSch = , the set of semantic

knowledges about our domain of interests, which is

proteomics.

The concepts annotations, defined

proteomicsO' will serve to enrich Global query

before rewriting process. The semantic mappings

will show query answering capabilities of the

underlying sources.

Given a Global query

Q and the knowledges

couple

O'Sch , our rewriting approach consist to

determine two sub-queries

valide

Q and

invalide

Q .

Explicitly, we shall calculate:



invalide

Q''Q = having a size as minimal as

possible. The Size of a query is the number of

atomic goals that it contains. Sub-Query

''Q

cannot be answered by underlying sources, at

the moment of the sending of the Global

query

Q . This initial operation has the role of

cleaning up

of domain concepts/properties

which are not yet available, as Web

proteomics registered resources. So, no

processing will be realized on

''Q , in the

future.



valide

Q'Q

is the part of Q that will be

rewrite using semantic mappings

M of

O'Sch . Sub-query 'Q can be answered by

registered sources. Our final goal is to propose

an intelligent subdivision of

valide

Q'Q = into

sub-queries

'Q ,

'Q ,…,

'Q with nm1 ≤≤ ,

is the number of sources available in the

integration while

m denotes the number

sources which are necessary to provide an

answer to the query

Q . So, we might find the

set

{

}

)m,'Q('Q

of couples

)m,'Q(

such

be an atomic subdivision of 'Q that

will be answered by mapping

We can easily remark that several rewritings can

be proposed, we will call them Candidate rewritings.

In fact, more than one source, and so mapping, could

provide the same resources searched.

The algorithm receives as input a global

query

, a schema O'Sch and generate as output all

candidates’ rewritings

)Q(r

4.2 Hypergraph-based Algorithm

In practice, Global queries are expressed like

conjunctive queries using Trees-Logics. So, a

rewriting

is a suitable conjunction of constraints.

These constraints might be checked by all final

answers of the global query

Q , because they

constitute an indication of resources that may be

retrieved from adequate sources.

In order to provide a characterization of our

query rewriting problem, we give an alternative

formulation of the rewriting formalization.

Given a Global Query

Q and the semantic

knowledges couple

O'Sch , query rewriting consists

to compute two sub queries

valide

Q and

invalide

Q on

the basis of mappings set

, such as:

invalidevalide

QQQ

∧

(1)

We are searching for all candidates rewritings,

formulated as the conjunction of constraints:

1ivalide

C'QQ

(2)

All constraints

C are logical representation of the

user specific needs. Finally, our motivation is to

answer the fundamental question which is to find,

given

Q a new query called rewriting expressed by

ICEIS 2009 - International Conference on Enterprise Information Systems

126

1ivalide

C'QQ

such as

denotes as much as

possible the resources expected by query

Q ?

We have said that several and alternatives

rewritings are possible, due to the fact that more

than one mapping could be used to reformulate an

atomic goal of the Global query. From this point of

view, rewriting problem which requires generating

all candidates’ rewritings can be characterized as a

current Hypergraph Theory problem of computing

all minimals Transversals of an Hypergraph.

Generate a Transversal Hypergraph consists of

generate all minimals Transversals.

4.2.1 Definition of Hypergraph (Kavvadias,

2005)

An Hypergraph

is an ordered pair ),( EVH

where

{}

n21

v,...,v,vV = is a finite set of elements

and

{}

m21

E,...,E,EE = is a family of subsets of

such that

E )m,...,1i(, =

∪

The elements of

V are called nodes while the

elements of

E are called hyperedges of the

hypergraph

. A hypergraph can be seen as a

generalization of a graph where the restriction of an

edge having only two nodes does not hold.

4.2.2 Definition of Transversals (Kavvadias,

2005)

Let )E,V(H = be an hypergraph. A set VT ⊆ is

called a Transversal of

if it intersects all its

hyperedges, i.e,

ET EE,

. A transversal

is called minimal if no proper subset '

of T is a

transversal of

The Transversal Hypergraph

)H(Tr of an

hypergraph

is the family of all minimal

transversals of

From a rewriting query problem, we need to give

a mathematical characterization, by defining an

associated Hypergraph

)E,V(H

M,Q

, built as

follows:

 For every mapping

m , describing a local

concept from

, as a logical function of

O’proteomics global concepts, we associate a

vertice

V in the hypergraph

)E,V(H

M,Q

and

[]

{

}

n,1i,VV

 For every constraint

C of the Global query Q ,

we associate an hyperedge

E in the

hypergraph

),(

EVH

. To simplify, we

suppose that all these constraints are

describing atomics goals. So, each

hyperedge

E is a set of mappings, calculated

by considering those mappings which are

relevant to answer these goals.

A classical algorithm to compute minimal

Tranversals of an hypergraph is proposed and

available in (Mannila, 1994). Many papers (Eiter,

1995) have discussed about algorithm of generation

of Hypergraph Transversal, which is a set of

minimal Transversals. One of the first results

remains Berge’s Algorithm (Berge, 1989), but

several variants have been proposed in order to deal

with the algorithm complexity (Rey, 2003).

Now, we present our Query rewriting algorithm

called Q-Candidates’Finder, which integrates the

better and efficient complexity of the classical

Algorithm:

Q-Candidates’Finder Algorithm.

Input: A Query Q and

mappings)M,proteomics(O'OSch' =

Output:The set

f candidates rewriting such

{

}

)

invalide

valide

candidates

Q =

1: Build the associated Hypergraph

),(

EVH

2: Compute

1iinvalide

= such as

is not

provided by any mappings in

M .

3: Build the associated Hypergraph

)E,V(H

M,Q

candidates

5: Generate the Hypergraph Transversal

)E,V(H

M,Q

- Let be HypTransv - Using the Classical

Algorithm [Mannila, 1994]

6: For all edge

{

}

HypTransvV,...,V,VX

p21

mmm

[]

{

}

pjmQQQrQ

jjvalide

,1),,'(')( ∈===

where

'Q is a subdivision of

valide

that will be answered by the mapping

validecandidatescandidates

QQQ ∪

9: End For

10 : Return

candidates

AN USER-CENTRIC AND SEMANTIC-DRIVEN QUERY REWRITING OVER PROTEOMICS XML SOURCES

127

4.3 Q-Candidates’ Finder Illustration

To illustrate the proposed rewriting approach, let us

consider the following mappings (L.A.V approach).

As the domain Ontology is characterized as a Tree,

semantic mappings might express subsomption

(Sub) and equivalence (Eq) relations that exist

between Local XML Schemas, also abstracted as

Trees, and the Ontology’s Tree model. We suppose

in order to simplify this illustration that we have

only simple paths mappings (and so, no sub-Trees)

between Concepts, according to 1:1 cardinality. For

every registerd proteomics’source, we provide the

LHS (Left Hand Side expressing Local

Concepts/Properties), the TYPE (the type of

mappings), and the RHS (Right Hand Side,

expressing Ontology Concepts/Properties) of the

current mapping.

Table 1: Mapping Table.

LHS TYPE RHS

O’proteomics

Ontology

Gene (Genes, Proteins, Species, Organisms)

Proteine (IdProteins, Peptides, DevStadium)

…

Mapping m1:

Description Of

Source 1

S1_Gene (

S1_GeneName,

S1_ProteinName;

S1_species,

S1_organisms)

…

Gene (

Genes,

Proteins,

Species,

Organism)

Mapping m2:

Description Of

Source 2

S2_Gene (

S2_NomGenes,

S2_NomProteine,

S2_Especes,

S2_Organismes)

….

Gene (

Genes

Proteins

Species

Organisms)

Mapping m3:

Description Of

Source 3

S3_TreeLife (

S3_Species,

S3_Genus…)

Sub

…

Gene (

Species,

Organisms)

We have just shown mappings which are

relevant for the Query we shall process. Note once

again, that we are considering corresponding paths

of these Concepts/Properties in their abstract Trees.

According to this mapping table, we can say that

the ontology includes Concept Gene and Proteine

with their relative Properties such as Genes,

Proteins, and Species … Mappings m1 and m2 show

that Source I and Source II provide the properties

such as Gene, Proteins, Species, and Organisms,

while the mapping m3 illustrate that Source III only

provides properties such as Species and Organisms.

Let us consider now the following query which is

expressed over the domain ontology, O’proteomics :

What are the genes which proteins could have a

peptide Signal and for which, it is assumed that they

are expressed at Tardive Shizont stadium for the

Plasmodium falciparum?

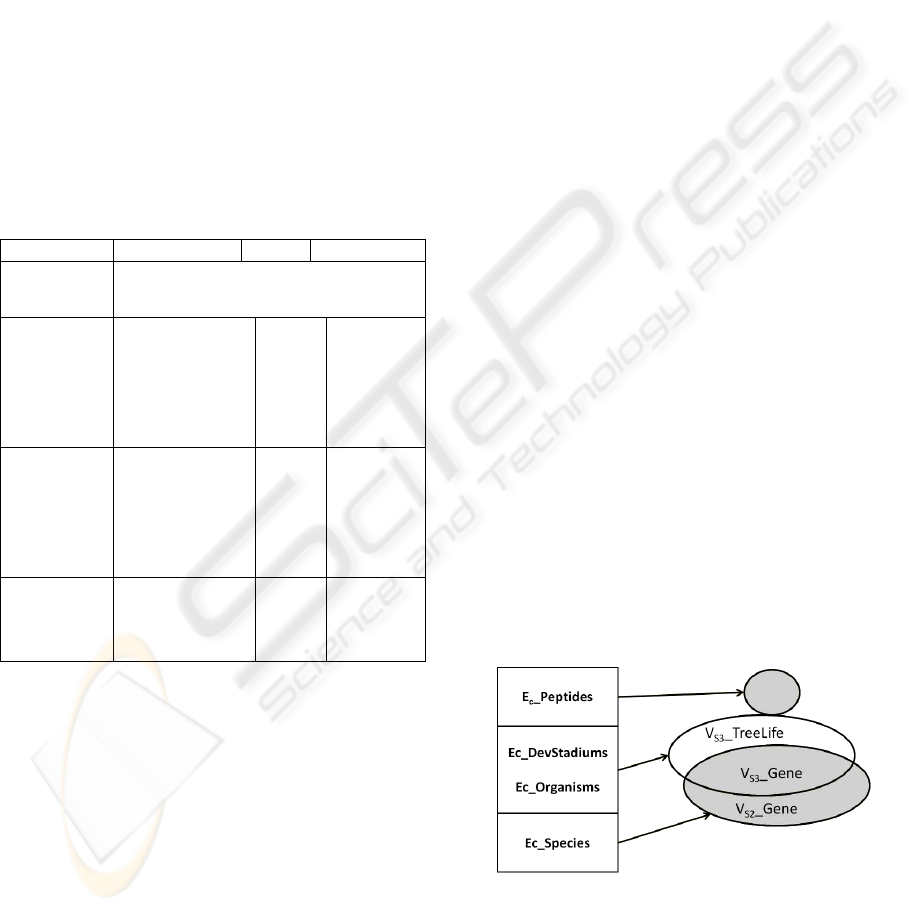
4.3.1 Hypergraph Construction

Intuitively,

can be expressed like a conjunction of

the following constraints:

SpeciesOrganisms

sDevStadiumPeptidesGenes

CCCQ

Proteins

∧

(3)

In practice, the user will formulate this request

by using an user-friendly graphic interface, and the

generation of its Trees-Logics version is done

automatically. He will choose the Concept Genes

and indicate for each property Gene, Proteins,

Species, Organisms, Peptides, DevStadiums the

expected values.

The associated hypergraph

),(

EVH

consists

of the following sets of vertices and edges:

{

}

3_1_2 TreeLifeSGeneSGeneS

VVVV

−

(4)

and

,,,

__Pr_

__,_

EE E

EEE

C Genes C oteins C Peptides

C DevStadiums C organisms C Species

⎧

⎫

⎪

⎨

⎬

⎪

⎩⎭

(5)

We could see this illustration using a

Sets’Theory point of view. We materialize all query

constraints as Sets that contain the providers’

mappings.

We show graphically these sets of mappings:

Figure 1: Associated Hypergraph of the illustration.

4.3.2 Determination of

invalide

Q is the part of Q that cannot be answered by

available sources. That means, we might constitute

ICEIS 2009 - International Conference on Enterprise Information Systems

128

invalide

Q with all Q ’s constraints, which are

characterized by empty hyperedges of

hypergraph

),(

EVH

We can easily see that no mapping provides the

hyperedges DevStadiums and Peptides. These

hyperedges are empty of associated mappings (Q-

Candidates’Finder: Line 2).

Hence:

sDevStadiumPeptidesinvalide

CCQ =

(6)

4.3.3 Determination of

valide

Q is the part of Q that can be answered by

available sources. That means, we might constitute

valide

Q with all

’s constraints, which are

characterized by non-empty hyperedges of

hypergraph

),(

EVH

So, we have:

SpeciesOrganismsGenesvalide

CCCQ C

Proteins

∧=

(7)

In fact,

valide

means that we could only answer

the following request, given semantic mappings:

Give the genes which code all proteins, for the

Plasmodium falciparum?

4.3.4 Determination of

candidates

From calculated above, we generate associated

hypergraph Hypergraph

),(

EVH

, (see Line 3).

Intuitively, according to Sets’Theory vision,

finding all candidates rewriting suppose firstly to

construct the Cartesian product of all sets of

mappings. It is obvious that Elements of the

Cartesian product are 4-uplets in our illustrative

example. So, we must generate for each 4-uplet, an

associated Set (These sets correspond to

Transversals). In fact, it will be useful to use a

minimal number of Sources that would be requested.

This condition is guaranteed if we consider only

associated sets that not contain another associated

Set (These sets are minimals Transversals). That is

why we call the Classical Algorithm (see Line 5).

The maximal cardinality of our example

Transversals is 4, it is the size of

valide

Q .

From Sets’Theory point of view we can say that

any set that contain

GeneS

and

GeneS

is a

Transversal and constitutes possible rewritings of

Q .

The minimal Transversal are

{}

GeneS

and

{

}

GeneS

constitute two candidates rewritings.

In our case, we could find 36 4-uplets, associated

with 6 Transversals but only 2 are minimal

Transversals.

5 CONCLUSIONS

This paper deals with Global query rewriting, which

consists in data integration context, to rewrite the

global query expressed in terms of concepts and

their properties defined in global schema domain

ontology) into suitable terms of local data sources.

The Query rewriting process is based on semantic

mappings. Our knowledge domain concern

Proteomics research, and so we have proposed

ontology according to interviews and talks with

biologists and bio-informaticians, called

O’proteomics. We provide a characterization of the

Query rewriting problem based on Hypergraph

Theory. We have presented the classiscal algorithm

that computes all minimals Tranvsersals, given an

Hypergraph. We observe that those minimals

Transversals correspond to Candidates rewritings of

the Global Query.

The formalization and the specification of the

proteomics semantic knowledges and some efforts to

find automatically mappings between the ontology

and the different local Schemas. Therefore, we need

to better defined a logical formalisme or language to

specify synatx and semantics data Trees. It could be

seen as a subset of Description Logics or based on

Psi-terms formalism. After this essential choice, we

will try to provide a prototype.

This paper shows briefly our current research

that aims to provide a semantic framework to realize

a Data Integration over XML bio-Sources on the

Web. We will define some relevant criteria to rank

candidates rewritings, necessary to select an optimal

and qualitative rewriting

optimal

Q . An efficient way

for selecting best rewritings, iteration by iteration,

will permit us to investigate the properties and the

optimiwation of our algorithm. These relevant

criteria could concern user preferences, quality of

underlying sources, etc…

REFERENCES

Amann, B., Beeri C., Fundulaki I., Scholl, M., 2002.

Ontology-based integration of XML web resources. In

Proceedings of International Semantic Web

Conference '02

, Pages: 117-131.

AN USER-CENTRIC AND SEMANTIC-DRIVEN QUERY REWRITING OVER PROTEOMICS XML SOURCES

129

Baader, F., Calvanese, D., McGuinness, D., Nardi, E.D.,

Patel-Schneider, P., 2003.

The Description Logic

Handbook, Theory, Implementation and Applications

Cambridge University Press, Cambridge.

Benatallah, B., Hacid M-S., Paik H-y., Rey C., Toumani

F., 2006. Towards semantic-driven, flexible and

scalable framework for peering and querying e-catalog

communities, In

Elsevier’s Journal of Information

Systems

, Pages: 266-294.

Berge, C., 1989.

Hypergraphs. North Holland,

Amsterdam, ISBN 0 444 874895; QA166.23.B4813.

Bishop, M., 1999. Genetics Databases, Academic Press.

Bray, T., Paoli, J., Sperberg-McQueen, 1998. “

Extensible

Markup Language (XML) 1.0

,” W3C February

Recommendation, available online at

http://www.w3.org/TR/REC-xml.

Davidson, S.B., Overton, C., Buneman, P., 1995.

Challenges in integrating biological data sources.

Journal of Computational Biology, 2(4):557–572.

Delobel, C., Reynaud, C., Rousset, M-C., Sirot, J-P.,

Vodislav, D., 2003. Semantic integration in Xyleme: a

uniform tree-based approach, In

Elsevier’s Journal of

Data & Knowledge Engineering

44, Pages: 267–298.

Deutsch, A., Tannen, V., 2003. Reformulation of XML

Queries and Constraints, In Proceedings of the 9th

International Conference on Database Theory (ICDT)

Pages 225-241.

Deutsch, A., Tannen, V., 2005. XML queries and

constraints, containment and reformulation,

Elsevier’s

Journal of Theoretical Computer Science

, 336 Pages:

57-87

Eiter, T., Gottlob, G., 1995. Identifying the minimal

transversals of a hypergraph and related problems.

SIAM Journal on Computing, 24(6), Pages: 1278-

1304.

Fundulaki, I., Amann, B., Beeri, C., Scholl, M., 2002.

STYX: Connecting the XML World to the World of

Semantics Web resources. In Proceedings of EDBT'

2002, Prague, Czech Republic

Gottlob, G., Koch, C., Schulz, K.U, 2004. Conjunctive

Queries over Trees, In Proceedings 23rd ACM

SIGMOD-SIGART Symposium on Principles of

Database Systems (PODS 2004)

, Paris, France. ACM

Press, New York, USA, Pages: 189-200.

Halevy, A., 2001. Answering queries using views: a

survey, In

Proceedings of Very Large Data Bases. 10

(4), Pages: 270–294.

Halevy, A., Ives Z., Tatarinov I., Mork P., 2003. Piazza:

Data management infrastructure for semantic web

applications

. In Proceedings of the International

World Wide Web Conference

Kavvadias, D., Stavropoulos, E., 2005. An Efficient

Algorithm for The Transversal Hypergraph

Generation, In

Journal of Graph Algorithms and

Applications

, Vol.9, No.2, Pages: 239-264.

Kohler, J., 2004. Integration of Life Science databases, In

Elsevier's Drug Discovery Today Journal,

BIOSILICO Vol.2, No.2.

Lehti, P., Fankhauser, P., 2004. XML Data Integration

with OWL: Experiences and Challenges, In

Proceedings of Symposium on Applications and the

Internet (SAINT'04), Pages: 160 -170.

Levy A., Rajaraman A., Ordille J., 1996. Querying

Heterogeneous Information Sources Using Source

Description

s, In Proceedings of Very Large Data

Bases Conference

, pages 251-262, Mumbai, India.

Mannila, H., Raiha, K-J, 1994.

The Design of Relational

Databases

. Addison -Wesley, Wokingham, England.

Manolescu, I., Florescu, D., Kossmann, D.K, 2001.

Answering XML queries over heterogeneous data

sources. In

Proceedings of the 27th International

Conference on Very Large Data Bases (VLDB ’01)

Orlando, Pages: 241–250.

Rey, C., Toumani, F., Hacid, M.-S., Leger, A., 2003,

algorithm and a prototype for the dynamic discovery

of e-services, Technical Report, LIMOS, Clemont-

Ferrand, France.

Schlieder, T., 2001. ApproXQL: Design and

Implementation of an Approximate Pattern Matching

Language for XML, Technical Report, Freie

Universitat Berlin.

Thompson, H.S., 2000. “XML Schema Part 1: Structures,”

W3C, work-in-progress, current as of Apr. 2000.

ICEIS 2009 - International Conference on Enterprise Information Systems

130