
FORECASTING TOTAL SALES OF HIGH-TECH PRODUCTS
Daily Diffusion Models and a Genetic Algorithm
Masaru Tezuka and Satoshi Munakata
Research and Development Section, Hitachi East Japan Solutions, Ltd.
2-16-10, Honcho, Aoba ward, Sendai, Japan
Keywords:
Demand forecast, Diffusion model, Genetic algorithm, New product.
Abstract:
In recent years, the release interval of high-tech consumer products such as mobile phones and portable media
players is getting shorter. New models of mobile phones are released three times a year in Japan. The manu-
factures have to avoid dead stock because the value of the previous model drops sharply after the launch of the
new model. In this paper, we propose a method to forecast the total sales of the products. The method utilizes
diffusion models for forecasting. Only short-term sales record is available since the sales are forecasted one
month after the release. In order to make effective use of the available data, we use a day as the time unit
of forecasting. To apply the diffusion models to daily demand forecasting, we derive the difference equation
representation of the models and propose discrete-time diffusion models. Day-of-week-dependent parameters
are introduced to the models. The proposed method is tested on the data provided by a high-tech consumer
products manufacturer. The result shows that the proposed method has an excellent forecasting ability.
1 INTRODUCTION
In recent years, the release interval of high-tech con-
sumer products such as mobile phones, portable me-
dia players, and PDAs is getting shorter. After the
launch of a new model of the products, the com-
mercial value and the sales of its previous model
drop sharply. Thus, the manufacturers have to sell
out the previous model before the launch of the new
model. At the same time, they have to avoid opportu-
nity losses in order to maximize profitability. Conse-
quently, accurate forecasting of the total sales of the
products just after the launch is desired.
New models of mobile phones are released three
times a year in Japan. That means their effective sales
period is only four months. In this paper, we propose
a method that the total sales of high-tech products in
four months are forecasted one month after the release
of the products.
Only short-term sales record is available since the
total sales are forecasted just one month after the re-
lease. In our case, only one-month sales record is
available. If the unit of time is a week, only four sales
records are available. However, if it is a day, so are 28
or more sales records. Thus, we use a day as the time
unit of forecasting.
Diffusion models(Mahajan et al., 2000) are used
to forecast the demand of new products. In order to
apply diffusion models to daily demand forecast, we
derive the difference equation representation of diffu-
sion models and discretize the models with respect to
time. A real-valued genetic algorithm is employed for
estimation of the parameters of the models.
2 DIFFUSION MODELS
In this section, four diffusion models are briefly re-
viewed. x(t) denotes the cumulative sales amount at
time t and dx(t)/dt represents the sales rate at time
t. On the assumption that a certain proportion p of
the consumers who have not yet bought the product
buy the product at time t, sales rate can be stated as
follows:
dx(t)
dt
= p(m− x(t)) (1)
where m is the market size. Solving (1), we obtain
negative exponential diffusion model as follows:
x(t) = f
NE
(t;m, p,τ) = m
1− e
−p(t−τ)
(2)
Logistic model assumes that the purchase is pro-
moted by word-of-mouth and the influence of word-
of-mouth is proportional to penetration rate x(t)/m.
335
Tezuka M. and Munakata S. (2009).
FORECASTING TOTAL SALES OF HIGH-TECH PRODUCTS - Daily Diffusion Models and a Genetic Algorithm.
In Proceedings of the 11th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
335-338
DOI: 10.5220/0001991903350338
Copyright
c
SciTePress

The sales rate can be states as follows:
dx(t)
dt
= q
x(t)
m
(m− x(t)) (3)
Solving (3), we obtain logistic model as follows:
x(t) = f
Log
(t;m, q,τ) =
m
1+ e
q(t−τ)
(4)
Bass model involves both external and internal in-
fluences. Its sales rate is stated as follows:
dx(t)
dt
=
p+ q
x(t)
m
(m− x(t)) (5)
Equation (5) corresponds to (1) when q = 0 and (3)
when p = 0. Solving (5), Bass model is:
x(t) = f
Bass
(t;m, p,q,τ) = m
p− pe
−(p+q)(t−τ)
p+ qe
−(p+q)(t−τ)
(6)
PNE(Power of Negative Exponential) model (Mu-
nakata and Tezuka, 2008) is an extension of negative
exponential model and is written as:
x(t) = f
PNE
(t;m, p,r,τ) = m
1− e
p(t−τ)
r
(7)
3 TOTAL SALES FORECASTING
ON DAILY BASIS
3.1 Problems of Daily Forecasting
Previous studies applied diffusion models to monthly
or weekly forecasting, i. e., the time unit of the model
is month or week. However, in this paper, the total
sales of a product, which are the cumulative sales in
four months or in 120 days, are forecasted on the 28th
day from the launch of the product.
When time unit of t is a day, sales rate dx(t)/dt
depends on the day of the week. Usually, more con-
sumers go to buy products on holidays than on week-
days. Thus, sales rate is higher on holidays than on
weekdays. That means the parameters of the diffu-
sion models have to be time-variant.
3.2 Derivation of Discrete-time
Diffusion Models
In order to apply the diffusion models to sales fore-
casting on daily basis, we derive the difference equa-
tion representation of diffusion models and discretize
the models with respect to time. Then, we introduce
parameters depending on the day of the week to the
models.
We modify the models and develop a discretized
negative exponential, logistic, Bass, and PNE models
as:
x
t+1
=
ˆ
f
NE
(x
t
,m, p) = m
1− e
−p
+
x
t
m
e
−p
, (8)
x
t+1
=
ˆ
f
Log
(x
t
,m, q) =
m
1+
m
x
t−1
− 1
e
q
, (9)
x
t+1
=
ˆ
f
Bass
(x
t
,m, p,q)
= m
q+ pe
−(p+q)
x
t−1
+
p− pe
−(p+q)
m
q− qe
−(p+q)
x
t−1
+
p+ qe
−(p+q)
m
,
(10)
x
t+1
=
ˆ
f
PNE
(x
t
,m, p,r)
= m
1− e
−p
+
x
t
m
1
r
e
−p
r
.
(11)
3.3 Day-of-Week-Dependent
Parameters
Parameter m, that is the market size, can vary over
time in the long-term depending on the economic con-
dition in the market. However, we assume that m is
time-invariant in the case of high-tech products whose
sales period is very short.
On the other hand, we assume that p, q, and r are
time-variant. They depend on the day of the week
because so do the behavioral pattern of consumers.
As mentioned before, they differ between on holidays
and on weekdays. Thus, we introduce parameters p
h
,
q
h
, and r
h
for holidays and p
w
, q
w
, and r
w
for week-
days.
Then, we have discretized diffusion models with
time-variant (day-of-week-dependent) parameters:
x
t+1
= g
·
(x
t
;m, θ
h
,θ
w
)
=
ˆ
f
·
(x
t
;m, θ
h
) if t + 1 is holiday
ˆ
f
·
(x
t
;m, θ
w
) if t + 1 is weekday
(12)
where θ
h
and θ
w
are {p
h
} and {p
w
} for the nega-
tive exponential model, {q
h
} and {q
w
} for the logis-
tic model, {p
h
,q
h
} and {p
w
,q
h
} for Bass model, and
{p
h
,r
h
} and {p
w
,r
h
} for PNE model.
3.4 Parameter Estimation With a
Genetic Algorithm
Sales record for T periods, s
1
,s
2
,...,s
T
are available.
The parameter estimation problem is formulated as
follows:
Min.
1
T − 1
T−1
∑
t=1
g
·
(s
t
;m, θ
h
,θ
w
) − s
t+1
2
(13)
ICEIS 2009 - International Conference on Enterprise Information Systems
336

subject to m− s
T
≥ 0
m, p
h
, p
w
,q
h
,q
w
,r
h
,r
w
≥ 0
p
h
− p
w
≥ 0
q
h
− q
w
≥ 0 (14)
Market size m can not be negative value and is
naturally larger than the latest sales amount s
T
. The
domains of the other parameters also have to be posi-
tive real number because the range of the function g,
that is forecasted demand, have to be positive.
The third and fourth constraints are based on the
empirical observation that the sales rate is larger on
holidays than on weekdays in our case. This observa-
tion certainly depends on the products.
Since g
·
(s
t
;m, θ
h
,θ
w
) is either of (8), (9), (10),
or (11) according to (12), the objective function of
the parameter estimation problem (13) is nonlinear
and complex. It is unable to estimate the param-
eters by solving normal equations or a linear least-
square method. From some preliminary experiments,
it is found that the solution obtained by quasi-Newton
method such as BFGS method highly depends on the
selection of initial search point and has large vari-
ance. Thus, we employed real-coded genetic algo-
rithms known as efficient optimization methods for
such problems(Eshelman and Schaffer, 1993; Fogel,
1997).
4 NUMERICAL EXPERIMENTS
The proposed total sales forecasting method is eval-
uated on the data provided by a high-tech consumer
products manufacturer. The data consist of the sales
record of seven models of their products for 120 days
from the date of release.
The sales record of the first 28 days, s
1
, s
2
, ..., s
28
are used for the parameter estimation. Then, x
29
, x
30
,
..., x
120
, are forecasted as:
x
t+1
=
g(s
28
;m, θ
h
,θ
w
), (t = 28)
g(x
t
;m, θ
h
,θ
w
), (otherwise)
(15)
The objective is to forecast total sales of a high-tech
product in four months. Thus, the absolute error on
120th day,
x
120
− s
120
s
120
(16)
is evaluated.
Since GAs are stochastic search algorithms and
their performance varies from time to time, ten runs
are performed with each model. Thus, 70 runs (10
runs multiplied by 7 models) are performed with each
diffusion model. Then mean and standard deviation
of the absolute error over 70 samples are evaluated.
The computation time required for one run con-
sisting of parameter estimation and demand forecast-
ing is as short as about 1 second on Microsoft Win-
dows XP PC with Intel Core Solo T1300 1.66GHz
and 1Gbytes RAM.
Table 1 shows the mean and standard deviation
(stdev) of the absolute error over 70 samples. For
comparison, the result of the conventional method,
which uses the diffusion models with time-invariant
parameters, is also shown. The proposed method
achieved better performance than the conventional
method. The mean forecasting error of the nega-
tive exponential model with the proposed method is
about 11% while with the conventional method is
about 44%. This is a considerable improvement. PNE
model with the proposed method also achieved a big
improvement.
T-test is conducted and the significance probabil-
ity between proposed method and conventional time-
invariant parameter method is shown. There are sig-
nificant differences between proposed and conven-
tional method.
Although the forecasting accuracies of the logis-
tic and Bass model are also improved with proposed
method, the forecasting error with the models is much
higher (worse) than the other models. We consider
that the logistic and Bass model themselves do not fit
the product we tested.
Figure 1 shows an example of the sales forecasted
with proposed and conventionalmethod and an actual
sales record. In the figure, actual sales slows down
on around 30th day by some unknown reason. Af-
ter that, however, the sales rate of the actual record
and the forecasts with the proposed method are al-
most same while the sales rate with the conventional
method declines gradually and the forecasts deviate
from the actual sales.
Figure 2 shows an another example of the fore-
casted and the actual sales. The figure is a close-up of
the data from 29th day to 42nd day. 33rd, 34th, 41st,
and 42nd day are holidays and you can see from the
figure that the actual sales rate on the days is higher
than the other days. The proposed method follows
the change of the sales rate while the conventional
method does not. Accumulation of the small differ-
ence of the sales rate results in a considerable differ-
ence of total sales forecasting.
5 CONCLUSIONS
In this paper, we proposed a method to forecast the
total sales of products whose effective sale period is
very short.
FORECASTING TOTAL SALES OF HIGH-TECH PRODUCTS - Daily Diffusion Models and a Genetic Algorithm
337
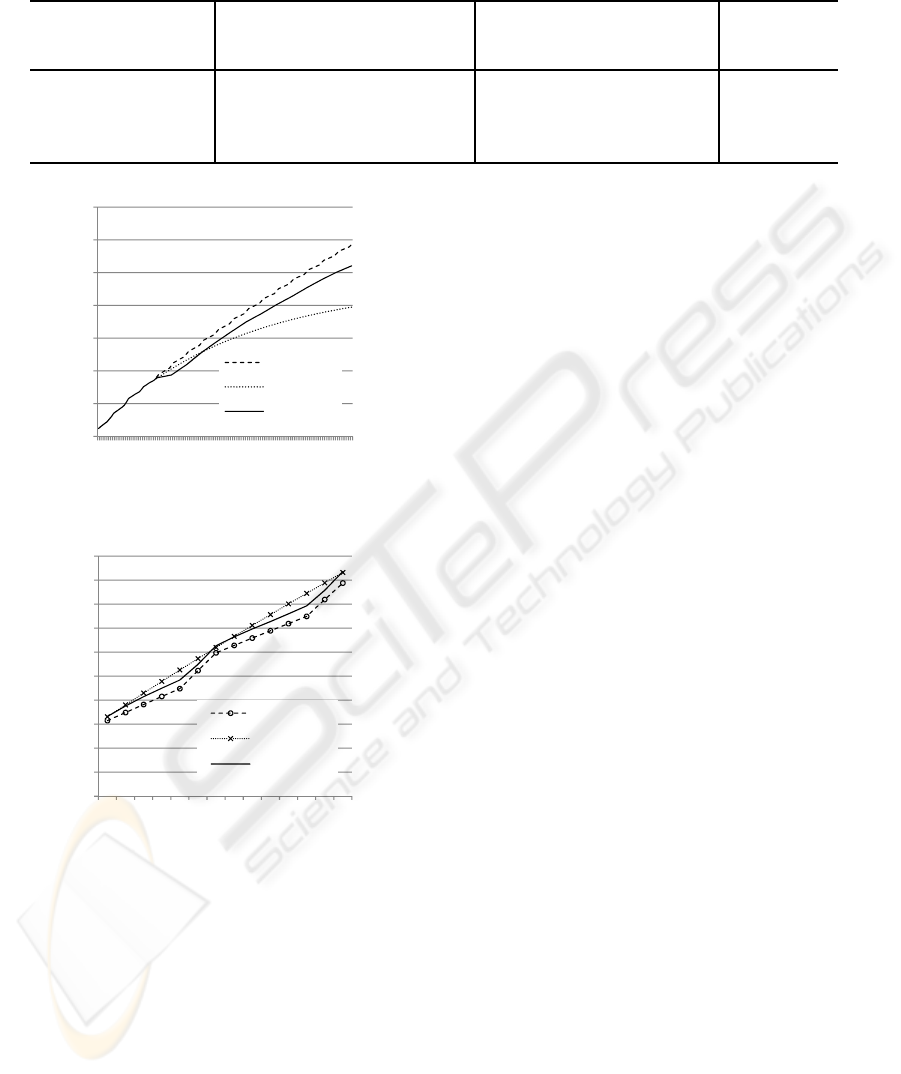
Table 1: Absolute errors of proposed method with time-variant parameters and conventional method with time-invariant
parameters.
Proposed discrete time model Conventional method significance
with time-variant params. with time-invariant params. probability.
mean variance mean variance
Negative Exponential 0.1121 0.0892 0.4425 0.2012 0.0000
Logistic
0.6353 0.0394 0.6825 0.0727 0.0000
Bass 0.3339 0.1835 0.5364 0.2286 0.0000
PNE
0.1563 0.1550 0.4448 0.2616 0.0000
250000
300000
350000
0
50000
100000
150000
200000
proposed
conventional
record
1
8
15
22
29
36
43
50
57
64
71
78
85
92
99
106
113
Figure 1: An example of the sales forecasted with proposed
and conventional method and an actual sales record.
270000
280000
290000
300000
200000
210000
220000
230000
240000
250000
260000
proposed
conventional
record
200000
29 30 31 32 33 34 35 36 37 38 39 40 41 42
Figure 2: Closeup of another example of the forecasted and
the actual sales.
The method uses the diffusion models to forecast
demand. It is better to forecast the total sales at the
earliest possible time. In this paper, it is forecasted
one month after the release of the new model. Since
only one-month sales record is available, we use a
day as the time unit of forecasting. In order to ap-
ply the diffusion model to daily demand forecast, we
derive the difference equation representation of diffu-
sion models and discretize the models with respect to
time. Then, day-of-week-dependent parameters are
introduced to the discrete-time diffusion models.
The parameter estimation is formulated as a lin-
early constrained non-linear minimization problem.
Since the objective function is non-linear, we em-
ployed a GA to estimate the parameters. We add sev-
eral practical constraints in order to reduce the search
space and to improve the optimization efficiency.
The proposed method is tested on the data pro-
vided by a high-tech consumer products manufac-
turer. Total sales in 120 days from the release of
their products are forecasted and compared to the ac-
tual sales record. The result shows that the proposed
method has an excellent forecasting ability.
REFERENCES
Eshelman, L. J. and Schaffer, J. D. (1993). Real-coded ge-
netic algorithms and interval-schemata. In Whitley,
L. D., editor, Foundations of Genetic Algorithms 2.
Morgan Kaufman.
Fogel, D. B. (1997). Real-valued vectors. In B¨ack, T., Fo-
gel, D. B., and Michalewicz, Z., editors, Handbook of
Evolutionary Computation, pages C1.3:1–1. Institute
of Physics Publishing and Oxford University Press.
Mahajan, V., Muller, E., and Wind, Y. (2000). New-Product
Diffusion Models. Kluwer Academic Publishers.
Munakata, S. and Tezuka, M. (2008). New diffusion model
to forecast new products for realizing early decision
on production, sales, and inventory. In Proceedings of
IEEE 8th International Conference on Computer and
Information Technology.
ICEIS 2009 - International Conference on Enterprise Information Systems
338
