MEASURING COORDINATION GAPS OF

OPEN SOURCE GROUPS THROUGH SOCIAL NETWORKS

Szabolcs Feczak and Liaquat Hossain

Faculty of Engineering and IT, The University of Sydney, PNR J05, Sydney, Australia

Keywords: Coordination gaps, Social Networks, Distributed Teams, Open Source Software.

Abstract: In this paper, we argue that coordination gaps, such as communication issues and task dependencies have

significant impact on performance of work group. To address these issues, contemporary science suggests

optimising links between social aspects of society and technical aspects of machines. A framework is

proposed to describe social network structure and coordination performance variables with regards to

distributed coordination during bug fixing in the Open Source domain. Based on the model and the literature

reviewed, we propose two propositions—(i) level of interconnectedness has a negative relation with

coordination performance; and, (ii) centrality social network measures have positive relation with

coordination performance variables. We provide empirical analysis by using a large sample of 415 open

source projects hosted on SourceForge.net. The results suggest that there is relationship between

interconnectedness and coordination performance and centrality measures were found to have positive

relationships with the performance variables of coordination measures.

1 INTRODUCTION

Coordination can be viewed as the additional

information processing required in order achieving

the same goal with multiple actors as one would do

alone. However, management of the dependencies

and efficient communication is required to minimise

coordination gaps. (Malone, 1988)

Previous studies focus on measures such as the

efficiency of communication and dependency

management, the quality of the outcomes, degree of

meeting requirements and deadlines for reducing

coordination gaps of project groups working towards

a common goal. (Rathnam & Mahajan & Whinston,

1995; Kraut, 1995; Faraj & Sproull, 2000)

Nevertheless, management of coordination for a

distributed team imposes higher variability in the

dependency management requirements and

therefore, makes the coordination much more

challenging compared to groups operating on the

same site and not having this sort of distance.

(Bonaccorsi & Rossi, 2003) Group awareness

therefore can help to raise the level of efficiency

through implicit coordination. (Gutwin, 2004)

Since one major facet of coordination is

communication, it is important to study relation

between network structures and coordination

performance in a distributed environment. Centrality

has been identified to have major positive influence

on coordination performance in local teams, but has

not been confirmed yet on large scale. (Rathnam,

1995) Therefore, analysis of coordination problems

in dynamic and dispersed collaboration groups

through their social structure is considered to be an

important area of research.

In social networks centrality denotes the

structural power position of a node in a given

network. Centrality has three measures (a) Freeman

degree centrality - number of adjacent nodes, (b)

closeness - reciprocal value of the total number of

hops in the shortest possible way to every other

node. and (c) betweeness - number of times the node

appears on the shortest path between other nodes.

The higher the value is the more influence can a

particular node has on the entire network. Centrality

is not only understood on nodes, a characteristic

value can be calculated for the total network as well

using any if the above measures. Network density is

the number of links divided by the number of all

theoretically possible links. (Robert & Hanneman,

2001; Freeman 1979)

There are several studies in the open source

domain looking for answers regarding coordination.

(Madey & Freeh & Tynan, 2002; Spaeth, 2005)

Feczak S. and Hossain L. (2009).

MEASURING COORDINATION GAPS OF OPEN SOURCE GROUPS THROUGH SOCIAL NETWORKS.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Human-Computer Interaction, pages 84-90

DOI: 10.5220/0001994200840090

 SciTePress

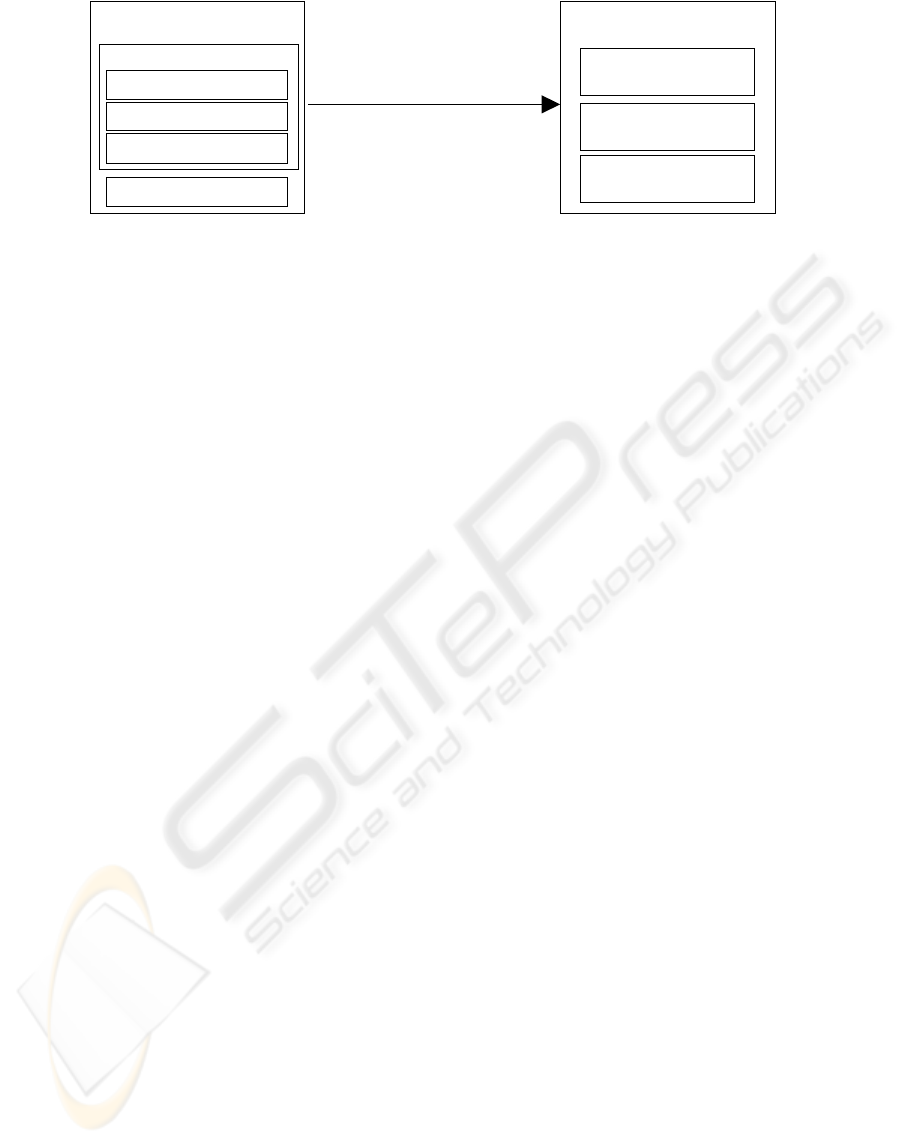
Coordination performance

(Dependent Variables)

Social Network Structure

(Independent Variables)

Network Densit

etwee

ess

Mean Time Between

Failure

Defect Removal

Effectiveness

ReciprocalTime To Fix

ose

ess

Centrality Measures

Figure 1: OSS Coordination performance model.

“Free and Open Source Software development not

only exemplifies a viable software development

approach, but it is also a model for the creation of

self learning and self-organising communities in

which geographically distributed individuals

contribute to build a particular software.” (Sowe &

Stamelos & Angelis, 2006) Consequently, open

source as a domain for this study was chosen for

exploring coordination performance measures.

2 COORDINATION THEORY

FOR OSS

We apply coordination theory for exploring the

effective coordination structures of open source

software teams engaged in bug fixing activities.

Using research findings of Sandusky and Gasser’s

study (Sandusky, 2005), we highlight the tasks

below which relates to coordination process by

incorporating normative software management

processes identified in open source environment: (i)

Goals: ensure that the software (i.e., is able to

perform all specified functions); (ii) Tasks (i.e.,

production tasks--identify the defect); (iii)

coordination tasks (i.e., report a bug, categorize a

bug: which module does it relate to, what is the

severity, priority); (iv) Actors-open source software

community members (i.e., one ore more developers

in various roles); and, (v) Dependencies (i.e., the

most common dependencies are from the producer-

consumer type). Dependency management is

performed in order to achieve the ultimate goal with

multiply actors: software without defects. Therefore,

effectiveness of the coordination is measured against

bug fixing task performance. Technical environment

has a moderating role in the information technology

domain (Rathnam & Mahajan & Whinston, 1995),

however these tools do not have ultimate effect on

coordination performance. Study by Kraut, and

Streeter suggest that project size and complexity

increases coordination gaps so these have been

added to the moderating variables as well (Kraut &

Streeter, 1995). With regards to the features of the

distributed team, experience was advised as a factor

which plays an important role in coordination,

providing a base for better understanding peers and

work flows to carry out internal coordination

without excessive communication (Faraj & Sproull,

2000). The number of the members in the team

relates to the size of the project so it has been added

to extend work group features.

To measure coordination performance, we

consider time constraint as it has direct correlation

with coordination performance (Espinosa, 2002).

Since coordination performance itself is not tangible

it is common practice to relate this measure to the

outcome of the work actors have completed

(Rathnam & Mahajan & Whinston, 1995).

Evaluation of the outcome could be done with

interviewing the users, however we do not have the

resources to do that, so the rating which relates to

dependency management is going to be done with

software evaluation methods discussed above (Kraut

& Streeter, 1995). Therefore, software quality

metrics are going to used to extend the timeliness

measure and evaluate coordination performance.

Figure 1 presents the elements of the framework and

relations between them. In developing this

framework, previous studies of coordination and

software development were analysed. After

identifying certain metrics, a preliminary test was

carried out to investigate if it is feasible to measure

those values advised by the literature. Based on the

availability and reliability of data accessible, the

measures were short listed. Based on the literature

and the model, we propose the following

propositions for this study: (i) higher degree of

network density creates redundant information flows

which have a negative effect on the coordination

performance; and (ii) higher degree of centrality and

betweenness creates stricter hierarchy, which

significantly reduces the dependencies, and

coordination gaps.

MEASURING COORDINATION GAPS OF OPEN SOURCE GROUPS THROUGH SOCIAL NETWORKS

3 METHODS

Most data about open source projects are publicly

available. However the number of projects is large

and they are scattered all over the world.

Furthermore, the services they use are not

homogeneous, and comparing many projects with

distinct technological characteristics in an unbiased

manner would be very tedious. Based on the above it

has been decided to use one of these major hosting

facilities as a source of data with a combination of

manual investigation of the preliminary selected

limited number of projects to check if they actively

use the services offered. The choice on SourceForge

was made based on the possibility that we could

have SQL access to monthly data dumps granted

through the Notre Dame University, Indiana, United

States. During the data set definition the following

aspects were kept in mind, to acquire as

representative data set as possible: (i) avoid

prominent projects; (ii) avoid projects with

gatekeepers; (iii) size of the project: around ten to

derive meaningful network structures; (iv) select

projects which have distinct characteristic to help

answering our questions, with minimum 200

interactions; and, (v) the project should be active in

bug fixing.

3.1 Network Data for Social Structure

Measures

First a list of the bug fixing contributors of the

selected projects was extracted grouped by

communication thread. Each unique participant is

identified by going through all lines and adding the

identifier to a vector if it does not contain it yet. An

empty adjacency matrix can be formed based on

that. Going through the lines again sorted by time,

we count the number of times an actor could see a

post from another actor in the thread before him/her,

this count becomes the weight of the link. It is

assumed that actors who submitted a post earlier

than someone else do not read the ones followed by

them unless they post again in the thread.

Interactions within each thread counted separately,

so even if two actors follow each other on the

timeline it does not count if it was on a different

thread. At the end of this process the matrix is

symmetrised based on the smaller number of

interactions. During the measurement, the threshold

was set to minimum five interactions to consider a

link significant (Adamic, 2005).

3.2 Coordination Performance

Measures

Time to Fix and Mean Time Between Failure

characteristics were measured based on the bug

tracking system records available from the database.

The Time to Fix index was calculated as an average

of differences between the open and the close date.

Mean Time Between Failure index was calculated as

an average of differences between the open time of a

bug and the open time of the bug before that bug in

consecutive timely order. Based on the histograms,

the variables did not follow normal distribution,

descriptive statistics confirm this, because all

skewness and kurtosis highly deviate from zero.

The Defect Removal Efficiency (DRE)

D(415)=0.141, p<0.001, Mean Time Between

Failure (MTBF) D(415)=0.130, p<0.001, and

Reciprocal Time To Fix D(415)=0.206, p<0.001

were all significantly non-normal.

"Density is a measure that is difficult to use in

comparisons of graphs of radically different sizes"

(Scott, 2000) Comparing work group performance

largely different in size would not be realistic either.

Therefore cluster groups were created based on the

frequency distribution of the node numbers in the

sample. Small (4-12 nodes), middle (13-40 nodes)

and large (41-223) network clusters were created to

achieve minimal dispersion from the median of the

respective pool.

4 RESULTS

4.1 Proposition 1

A number of variables show negative correlation on

Table 1 with the density, however at the level of

0.05 it is only significant for the reciprocal time to

fix variable in the group with 13-40 nodes. Negative

effect of density on coordination can be explained

by the strength of the weak ties argument,

(Granovetter, 1973) which states that too densely

connected actors provide mostly redundant, already

known information to each other. This hinders

coordination performance, as the communication

does not move forward the solution of the problem it

just increases the delay in the cooperative work. This

delay effects the time to fix and as this lowers

efficiency the defect removal deficiency as well.

What further suggest this theory is, that it can be

seen that the relation of the density with RTTF is

higher than with DRE, so the effect on the defect

removal efficiency measure can be indirectly due

ICEIS 2009 - International Conference on Enterprise Information Systems

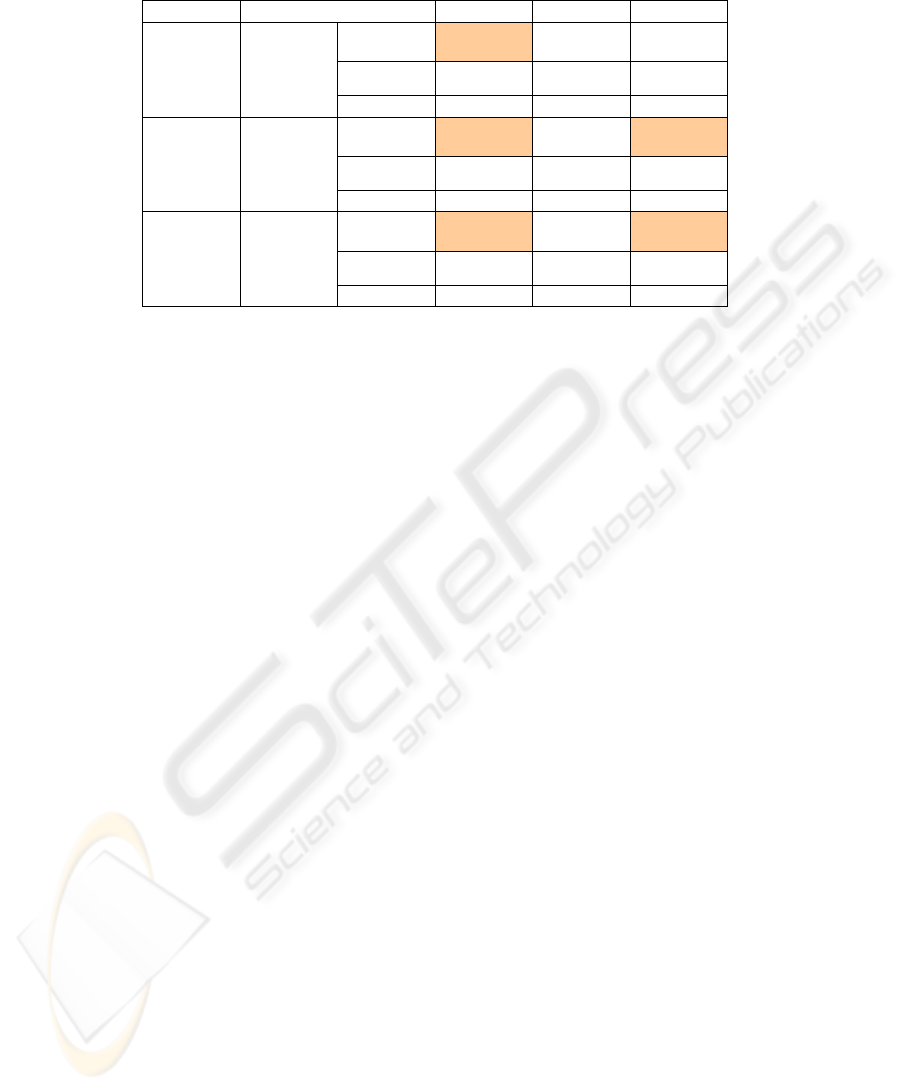
Table 1: Spearman Correlation grouped by nodes between Network Density and Performance variables (DRE: Defect

Removal Efficiency, MTBF: Mean Time Between Failure, RTTF: Reciprocal Time to Fix).

Node Group

Spearman's rho

DRE MTBF RTTF

4-12 Density Correlation

Coefficient

-.011 .108 .015

Sig. (2-

tailed)

.869 .088 .810

249 249 249

13-40 Density Correlation

Coefficient

-.182

.107 -.215

Sig. (2-

tailed)

.042

.237

.016

125 125 125

41-223 Density Correlation

Coefficient

-.086 .045 -.142

Sig. (2-

tailed

)

.594 .782 .376

41 41 41

**. Correlation is significant at the 0.01 level (2-tailed).

*. Correlation is si

nificant at the 0.05 level

(

2-tailed

)

to the increase caused in the time to fix. The p value

exceeding the significance level in the third group

(nodes 41-223) can be accounted to the high value of

standard error (47.17) of the node numbers in that

group. "Density is a measure that is difficult to use

in comparisons of graphs of radically different sizes"

However the above statistics do not apply to all

groups, but the coordination gaps were identified by

Rathman (Rathnam & Mahajan & Whinston, 1995)

to increase with the higher level of

interconnectedness and network density is also

referred as the degree of interconnectedness of

network members (Rober & Hanneman, 2001)

Again, Spearman correlation test is used to quantify

relations between centrality measures and variables

suggesting coordination performance.

4.2 Proposition 2

Centrality measures indeed show correlation with

coordination performance measures at the

significance level of 0.05. The positive relation can

be seen in all groups, on Table 2, the first which

applies to all of them is between Degree centrality

and the Reciprocal Time to Fix. Degree centrality

suggests activity so the network has more actors

with higher level of degree centrality the more

information is flowing through more active nodes

reducing the time gap between the sequence of

actions.

Mean time between failure has also positively

related to Degree centrality in the groups with nodes

4-40. This suggests not only efficient fixing of the

problem but also higher level of effectiveness. At a

significance level of 0.1 the same thing is true in the

large networks with 41-223 nodes as well. This

difference in significance can result from unclean

sample, or that the standard deviation of the node

numbers in this group is much higher (47.17)

compared to the two other groups. (2.53, 7.59). It is

interesting to see that closeness centrality has

positive correlation within all groups with Mean

Time Between Failure and Reciprocal Time to Fix.

Closeness centrality was identified to express

independence (Freeman, 1979) and a good predictor

on leadership. However it contradicts the general

belief that open source software development is

decentralised: “in practice tends to be more of a

peer-to-peer network topology than a military-style

command structure.” (Fogel, 2005)

There is an increasing weight in the relation as

we go from smaller networks to larger ones,

meaning that the more actors are in the coordinated

system the more effect a leader has on the

coordination performance. It seems that open source

is no exception under the rule, that coordinating

software development requires leadership and in a

distributed environment this is even more the case

(Lings, 2006). Leadership was also identified to

have high influence on selecting the best fitting

solution. (Bonaccorsi & Rossi, 2003) It explains

why the MTBF value becomes better, if a better

solution is selected to fix a problem it is probably

more reliable than other solutions. This is in line

with the other relation that Betweenness is positively

correlated with MTBF, if the leader is in a position

to control information, it can positively effect the

bug fixing coordination efficiency. This can be seen

among all clusters as well. There is also relation

between Betwenness and RTTF in the middle

cluster, also at the level of 0.1 it is also related in the

small group, so all together from 4-40 nodes. Again

the high value of the standard error in the large

MEASURING COORDINATION GAPS OF OPEN SOURCE GROUPS THROUGH SOCIAL NETWORKS

Table 2: Spearman Correlation grouped by nodes between Network Centrality measures and Performance variables (DRE:

Defect Removal Efficiency, MTBF: Mean Time Between Failure, RTTF: Reciprocal Time to Fix).

Node Group

Spearman's rho

DRE MTBF RTTF

4-12 Degree Correlation

Coefficient

-.015 .145

.130

Sig. (2-

tailed)

.809

.022 .040

249 249 249

Closeness Correlation

Coefficient

-.021 .140

.145

Sig. (2-

tailed)

.746

.027 .022

249 249 249

Betweenness Correlation

Coefficient

-.015 .158

.111

Sig. (2-

tailed)

.820

.013

.079

249 249 249

13-40 Degree Correlation

Coefficient

.099 .246

.229

Sig. (2-

tailed)

.272

.006 .010

125 125 125

Closeness Correlation

Coefficient

.124 .217

.209

Sig. (2-

tailed)

.169

.015 .019

125 125 125

Betweenness Correlation

Coefficient

.099 .297

.176

Sig. (2-

tailed)

.272

.001 .049

125 125 125

41-223 Degree Correlation

Coefficient

.156 .267 .311

Sig. (2-

tailed)

.329 .091

.048

41 41 41

Closeness Correlation

Coefficient

.204 .316

.348

Sig. (2-

tailed)

.201

.044 .026

41 41 41

Betweenness Correlation

Coefficient

.139 .319

.249

Sig. (2-

tailed)

.387

.042

.116

41 41 41

**. Correlation is significant at the 0.01 level (2-tailed).

*. Correlation is significant at the 0.05 level (2-tailed).

group (41-223) can contribute to the fact that the

correlation does not reach the required level of

confidence. In conclusion, all centrality measures

are positively related with most of the coordination

performance variables so the stricter hierarchy

reduces the gaps in coordination. It has to be noted

that DRE was not related to any of the centrality

measures. Probably it is an implication of the

domain, since stability (which is related to MTBF)

considered to be more important than prompt and

frequent activities (Edwards, 2001). MTBF shows

high importance as the relation with centrality

measures is 8 out of 9 possible times among the

three groups. MTBF suggests stability, since if the

software operates without problems for longer

periods it requires less bug fixing work, and

consequently less coordination. The opposite is true

as well, if the MTBF drops, the work load

significantly increases. “If stability is not achieved,

the need for communication within the project will

significantly increase” (Fenton & Neil, 1999) This

communication overhead than results in larger

coordination gap.

4.3 Project Level Analysis

Scummvm project for example, which is large

enough for this level of analysis it can be seen that

ICEIS 2009 - International Conference on Enterprise Information Systems

the number of permanent nodes is positively related

with the density of the network. That means that

over the time the more nodes stay permanent in the

network the more dense relationship they form.

However this density is negatively related with the

number of total nodes, so in case of a large network

the nodes are more loosely connected. As density

has positive effect on the error rate, so programmers

can produce more error free lines it is desired to

have the network built up from smaller dense

groups. These smaller work groups can interact

more efficiently and specialize on a specific area of

the code, which brings us to modularity. The code or

in general the work to be done must be broken down

into pieces which are analogical with the structure of

the team, or the other way round, smaller teams

should be organised around each problem areas. If

this out of synch that can raise issues with unclear

lines of responsibility, requiring more

communication which we can account as an

overhead, deteriorating the overall performance.

(Hinds & Kiesler, 2002) This is even more critical in

case of largely distributed work groups, since there

are limited possibilities for face to face interactions

and therefore the delay is typically longer between

exchanges. Even through phone conversations the

communication is less effective and due to time zone

differences the mutual time frames of availability

can be very short. (Wellman, 2000)

Short phases account for less number of errors as

seen on the evidence presented resulting in better

performance. A shorter work phase or milestone is

advantageous to accomplish goals on a smaller

scale, some ideas based on short cycles were coined

by the literature earlier for example the agile project

management concept. However shorter project

periods in case of an open environment have a

negative effect on engagement. Meaning that there is

less chance to attract more contributors to the project

and even those who are engaged typically stay only

till the end of the period. In case of a longer project

phase the turnover of the participants will be higher

and with people coming and going all the time there

is less chance to form a dense network compared to

a group with mostly steady memberships. Hence we

loose performance because of a more loosely

connected network. So on one hand we gain

performance efficiency with the shorter stages

through less turnover and more dense network, but

on the other hand as a result of smaller number of

people engaged the productivity is lower.

More people in the group ignites higher

productivity, but at the same time it raises other

issues. Without sound basic principles and strong

keep it simple policy more participants can have

very different ways of solving problems. This can be

good because it opens a possibility for innovation,

however it can easily increase work complexity,

uncertainty and the number of tasks that can not be

solved with best practices or routine procedures in

the future. (Kraut, 1995) In case of a distributed

environment more people can mean higher

effectiveness, but the efficiency can drop if the

leadership is not strong enough and with the lack of

clear guidelines which can induce internal

coordination without communication

overhead.(Espinosa, 2002, Gutwin, 2004)

Leadership brings us to the importance of

centrality and in fact as outlined above higher degree

of centralization increases the time between the

issues with the quality of the work reported.

Meaning that centrally located people can influence

the main direction of the project and increase the

quality and reliability of the work grounding a more

uniform work environment and clear vision about

what are the major goals. (Bonaccorsi & Rossi,

2003) It is interesting to note however that

betweenness centrality has negative effect on

productivity because the more betweenness the

network has the more time it takes to finish a task. In

local teams the betweenness network variable is

expected to project better team performance,

however in distributed teams people sitting in the

information flow can delay the process specially if

they act as bridges and they are the only ones who

connect segments of the network. If the node in

question is too busy or not available and the

information can not flow through any other node

towards the destination that significantly decreases

the reactivity of the team and as a result the overall

work group performance. Based on this it would be

useful to monitor the work load of nodes with high

betwenness score and match it against total team

reactivity.

Yet another interesting finding is that in an open

environment raising number of issues can actually

have positive influence on the team structure

because it raises the awareness about the possibility

to contribute and urge the users to do so. (von

Hippel, 2005) As a result the total number of nodes

in the network increases and opens possibilities for

future collaboration and innovation as these new

nodes when they join are only loosely connected so

they can refresh the redundant information within

the network with new ideas.

MEASURING COORDINATION GAPS OF OPEN SOURCE GROUPS THROUGH SOCIAL NETWORKS

5 CONCLUSIONS

Empirical evidence with an argument was provided

to show that centrality has importance in

performance of distributed coordination. Network

centrality properties shown positive relationship

with Mean Time Between Failure and Reciprocal

Time To Fix. We can conclude that centrally has a

bearing on coordination in distributed environments.

However bridging entities can slow down the flow

of information, because time distances can be

significant between nodes, therefore too high level

of betweenness is not beneficial. The implication of

this, that modularity might be important for large

projects (Hinds & Kiesler, 2002), but even in the

open source domain at least an informal centrally

positioned leader is required to enhance the

efficiency of a distributed work group. Although the

significance exceeded the confidence level in two

out of three clusters regarding the negative relation

between density and coordination performance, but

based on the results at least it is arguable that density

has positive effect on coordination. The results show

similarities with the results of Rathman (Rathnam &

Mahajan & Whinston, 1995). This finding is

interesting because their study was not in distributed

environment, however the results indicating that

similar relation exists in distributed environments.

The relation might not as strong as other theories

suggest that distributed work groups need

interconnections due to the temporal and

geographical distances they have to communicate

asynchronously (Crowston, 2005)

REFERENCES

Adamic, L. and E. Adar, How to search a social network.

Social Networks, 2005. 27(3): p. 187-203.

B. Wellman, J. Salaff, D. Dimitrova, L. Garton, M. Gulia,

and C. Haythornthwaite, "Computer Networks as

Social Networks: Collaborative Work, Telework, and

Virtual Community," Knowledge and Communities,

2000

Bonaccorsi, A. and C. Rossi, Why Open Source software

can succeed. Research Policy, 2003. 32(7): p. 1243-

1258.

C. Gutwin, R. Penner, and K. Schneider, "Group

awareness in distributed software development,"

Proceedings of the 2004 ACM conference on

Computer supported cooperative work, pp. 72-81,

2004.

Crowston, K., et al., Hierarchy and Centralization in Free

and Open Source Software Team Communications.

Knowledge, Technology, and Policy, 2006. 18(4): p.

65-85.

E. von Hippel, Democratizing innovation: MIT Press,

2005.

Edwards, K., Towards a theory for understanding the open

source software phenomenon. New Definitions: Value,

Community, Space, 2001.

Espinosa, J.A., et al., Shared Mental Models, Familiarity,

and Coordination: A Multi-Method Study of

Distributed Software Teams. Intern. Conf. Information

Systems, 2002: p. 425-433.

Faraj, S. and L. Sproull, Coordinating Expertise in

Software Development Teams. Management Science,

2000. 46(12): p. 1554-1568.

Fenton, N.E. and M. Neil, Software metrics: successes,

failures and new directions. The Journal of Systems &

Software, 1999. 47(2-3): p. 149-157.

Fogel, K., Producing Open Source Software. 2005:

O'Reilly.

Freeman, L.C., Centrality in social networks: Conceptual

clarification. Social Networks, 1979. 1(3): p. 215-239.

Granovetter, M.S., The Strength of Weak Ties. American

Journal of Sociology, 1973. 78(6): p. 1360.

Hinds, P. and S. Kiesler, Distributed Work. 2002: MIT

Press.

Kraut, R.E. and L.A. Streeter, Coordination in software

development. Communications of the ACM, 1995.

38(3): p. 69-81.

Lings, B., et al., Ten Strategies for Successful Distributed

Development. The Transfer and Diffusion of

Information Technology for Organizational

Resilience, IFIP, 2006. 206: p. 119-137.

Madey, G., V. Freeh, and R. Tynan, The open source

software development phenomenon: An analysis based

on social network theory. Americas Conference on

Information Systems (AMCIS2002), 2002.

Rathnam, S., V. Mahajan, and A.B. Whinston, Facilitating

Coordination in Customer Support Teams: A

Framework and Its Implications for the Design of

Information Technology. Management Science, 1995.

41(12): p. 1900-1921.

Robert, A. and M.R. Hanneman, Introduction to social

network methods. Department of Sociology University

of California, 2001.

Sandusky, R.J., Negotiation and the coordination of

information and activity in distributed software

problem management. Proceedings of the 2005

international ACM SIGGROUP conference on

Supporting group work, 2005: p. 187-196.

J. Scott, Social Network Analysis: A Handbook: Sage,

2000.

Sowe, S., I. Stamelos, and L. Angelis, Identifying

knowledge brokers that yield software engineering

knowledge in OSS projects. Information and Software

Technology, 2006. 48(11): p. 1025-1033.

Spaeth, S., Coordination in Open Source Projects, in

Graduate School of Social Sciences University of St.

Gallen

T. W. Malone, "What is coordination theory?," in National

Science Foundation Coordination Theory Workshop,

1988

ICEIS 2009 - International Conference on Enterprise Information Systems