MINING PATTERNS IN THE PRESENCE OF DOMAIN

KNOWLEDGE

Cláudia Antunes

Instituto Superior Técnico, Technical University of Lisbon, Av. Rovisco Pais, Lisboa, Portugal

Keywords: Pattern mining, Domain knowledge.

Abstract: One of the main difficulties of pattern mining is to deal with items of different nature in the same itemset,

which can occur in any domain except basket analysis. Indeed, if we consider the analysis of any

transactional database composed by several entities and relationships, it is easy to understand that the

equality function may be different for each element, which difficult the identification of frequent patterns.

This situation is just one example of the need for using domain knowledge to manage the discovery process,

but several other, no less important can be enumerated, such the need to consider patterns at higher levels of

abstraction or the ability to deal with structured data. In this paper, we show how the Onto4AR framework

can be explored to overcome these situations in a natural way, illustrating its use in the analysis of two

distinct case studies. In the first one, exploring a cinematographic dataset, we capture patterns that

characterize kinds of movies in accordance to the actors present in their casts and their roles. In the second

one, identifying molecular fragments, we find structured patterns, including chains, rings and stars.

1 INTRODUCTION

The growing interest in data mining and its maturity

have contributed to enlarge its application areas. In

parallel, this enlargement got several new challenges

into the arena, like dealing with complex data, but

also old ones, like the need to incorporate

background knowledge into the mining process.

The importance of introducing existing

knowledge in the core of the process is even stronger

in the case of pattern mining, where the balance

between the quantity and quality of the results are

far from being satisfactory. The goal of pattern

mining is to find the set of recorded facts that occur

simultaneously, a significant number of times.

Naturally, this number is a user defined parameter,

and depending on it the mining process returns a few

or thousands of patterns. The solution adopted to

achieve better results, has been the use of

constraints, from interestingness measures in

transactional data, to structural constraints defined

by formal languages in sequential pattern mining.

However, and since the primary goal of data mining

is to find unknown information, by constraining the

mining process we take the risk of turning the

process into a hypothesis testing task. In this paper,

we discuss how this risk can be managed by using

the Onto4AR framework recently proposed. In

particular, we make obvious that the framework

provides the tools necessary to warrant that no valid

patterns are ignored, and in addition, we show how it

makes possible the use of domain knowledge in the

discovery of patterns, either composed by concrete

or abstract items.

The rest of the paper is organized as follows:

next (in section 2), we overview constrained pattern

mining. Along this, we discuss the difficulties that

the use of constraints introduce. In section 3, we

review the Onto4AR framework, explaining how it

addresses the main difficulties identified so far, and

discussing what are its major weak points, stating

concrete ways to approaching and solving them. The

paper ends with some conclusions and pointing out

the directions to follow in future research.

2 PATTERN MINING

Pattern mining is a subtask of mining association

rules, a problem that was formulated in 1993 in the

context of basket analysis. Formally, let

I={i

,…,i

} be a set of m distinct liaterals, called

items and X⊆I a subset of items, therefore known as

itemset. Let D be a set of transactions, i.e., itemsets

transacted in the same conditions, under a unique

188

Antunes C. (2009).

MINING PATTERNS IN THE PRESENCE OF DOMAIN KNOWLEDGE.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

188-193

DOI: 10.5220/0001995001880193

 SciTePress

identifier. The goal of pattern mining is to find all

frequent itemsets in D, where X is said to be frequent

in D, if it is contained in at least σ%, with σ a

minimum support threshold defined by the user.

From these frequent itemsets is then possible to

generate all the association rules with support and

confidence above user-specified thresholds.

Association rules are just rules in the form A⇒B,

with A and B being itemsets (Agrawal 1993).

In a more generic formulation, itemsets are

replaced by sets of propositions, sets of pairs

attribute/value. In this manner, each item correspond

to one pair attribute / value, most of the times

representing only one attribute for some entity,

instead of an entire entity as in basket analysis. At

this point, some remarks have to be made about the

pattern mining phase.

First, the minimum support threshold, chosen by

the user, is the only factor that controls the mining

process, which means that all the responsibility of

mining results remains on the user hands. Certainly,

users are who better know the problem domain, and

are the best actors to establish the threshold under

what there is nothing interesting to see, but the

wrong choice can lead to the abandon of the

technique.

The second aspect to refer is related to the choice

of minimum support threshold. In fact, high levels of

minimum support leads to small sets of discovered

patterns, but most of the times, only trivial

information is found. At the other hand are low

levels of minimum support, that usually lead to very

large sets of discovered patterns, which to their huge

number, makes their analysis impossible.

Finally yet importantly, the user has been also

responsible for describing the transactions at the

proper abstraction level. Indeed, in the basket

analysis context, items do not correspond to real

instances but to some abstraction: when a customer

buys a Heineken Lager Beer, it can be bought by

other customer. Indeed, user has to choose if he want

to deal with the specific beer from Heineken, with

Heineken beers, or just with beers in general. Again,

the decision of the right level of abstraction

conditioned the number and relevance of each

discovered pattern. Note that the wrong choice, leads

to the necessity of re-describing the data and re-

running the entire mining process.

If it is undeniable that user should be in the

centre of the pattern mining process, by defining its

parameters and context, it is also certain that users

desire an integrated environment to control the

process, which provides simple mechanisms either

to choose parameters, and to evaluate the results, in

an iterative way. In order to provide such

environment, and makes pattern mining easier to the

final user, constraints have been proposed. A

constraint is a predicate on the powerset of the set of

items I, which means, that it is a function

c: 2

Æ{true, false}. An itemset S is said to satisfy c,

if and only if, c(S) is true.

In fact, constraints are the most effective

technique to reduce the number of discovered

patterns. As pointed in (Bayardo 2005), constraints

play a critical role in solving the trade-offs of the

generality of data mining algorithms, by focusing

"the algorithm on regions of the trade-off curves

known (or believed) to be most promising".

The greatest advantage of constraints is to

maintain the control of the mining process in the

hands of the user. Since he continues to assume the

responsibility of choosing which of aspects are most

important for the current analysis. In addition to this

responsibility, the user becomes to have a tool to

help him on choosing those aspects. Its greatest risk

is to reduce the discovery to a hypothesis testing

task, where the constraint has a too high level of

restriction, and filters off all the unknown

information.

One of the most used ways to contour this risk is

to use a special kind of constraint – an

interestingness measure. Interestingness measures

are constraints that impose quantitative conditions

over the set of items in the pattern or rule.

Interestingness measures rank the discovered

patterns or rules, by quantifying the usefulness and

utility of them, discarding those with an evaluation

less than the user-specified threshold. With these

constraints, it is possible to both improve the

performance of the algorithms, by pruning

uninteresting patterns, and reduce the number of

discovered patterns. However, all of them suffer

from the same difficult: to determine the value for

the threshold. As seen before, the choice of such

values determines the quality and quantity of the

results. And small variations on their value can have

dramatic impact.

On the opposite side of interestingness measures

are content constraints. Content constraints

correspond to filters over the content of the

discovered patterns, instead of its relevance. While

interestingness measures are quantitative metrics,

content constraints are predicates defined over the

value of the items that would be present in the

discovered patterns. In some sense, they try to

capture application semantics and introduce it into

the mining process.

The simplest one is item constraint that filters

out patterns that do not satisfy a Boolean expression.

MINING PATTERNS IN THE PRESENCE OF DOMAIN KNOWLEDGE

189

This determines the presence or absence of some

items, allowing for the discovery of patterns that

relate some specific known items with other

unknown ones. Being very simple, they have been

inherited and adopted by several other works, most

of the times in a too simplified way, restricting the

mining process to find the patterns that only contain

items from a pre-define set of items. More complex

content constraints can be found in the area of

sequential pattern mining. In (Garofalakis 1999) the

use of regular expressions (define through finite

automata – DFAs) were proposed for constraint the

discovery. Note that such restrictive constraints

increase the risk of turning the mining process in a

simple hypothesis-test. In order to solve this

antagonism, the use of constraint relaxations was

proposed (Antunes 2005). The idea is to pre-define

other classes of constraints that are defined over the

user-defined constraints. These new constraints

function as relaxations of the user-defined ones, by

allowing for the discovery of more patterns than the

original constraint.

The advances in the area of knowledge

management, verified in the last years, made

possible the incorporation of richer constraints in

non-structured problems. In particular, ontologies

have been used often. However, they have mostly

been used for post-processing purposes, which

means that instead of reducing the number of

discovered patterns and processing times, the goal is

to present just a subset of the discovered patterns to

the user, on accordance to his specification. The

Onto4AR framework (Antunes2007) is an exception,

and aims to provide the means to define constraints

to reduce the number of discovered patterns, and

simultaneously, improving processing times. Before

reviewing the framework, lets overview the relevant

notions in ontologies and knowledge bases.

The development of the Semantic Web

contributed considerably to advance the area of

ontologies, and now they are commonly accepted as

a mean to represent and share existing knowledge.

An ontology is a specification of an abstract,

simplified view of a domain. Formally, an ontology

is a 5-tuple O:={C,R,H

,rel,A

}. C is a set of

concepts, which represent the entities in the

ontology domain and R is a set of relations defined

among concepts. H

is a taxonomy or concept-

hierarchy, which defines is-a relations among

concepts: H

) means that c

is a sub-concept of

, or in other words c

is a parent of c

. The rel

element corresponds to a function, rel:RÆC×C that

specifies the relations on R: if r∈R, rel(r)=(c

also written as r(c

), and means that c

is related

to c

, but the inverse is not necessarily true. Finally,

is a set of axioms that describe constraints on the

ontology, making explicit implicit facts

(Maedche2002).

In the counterpart of ontologies are knowledge

bases, which specify existing instantiations for a

particular ontology. Formally, a knowledge base is a

4-tuple KB:={O, I, inst, instr}, where O is a

ontology as defined above and I a set of instances.

inst is a function from C to 2

called concept

instantiation, and instr the relation instantiation

function defined from R to 2

I×I

3 THE ONTO4AR FRAMEWORK

The Onto4AR framework is centred on the use of an

ontology and assumes a new formulation of the

problem, where the meaning of an item is clearly

defined in the context of the ontology.

Let KB:={O, I, inst, instr} be a knowledge base, and

D a set of transactions, where each transaction T is a

set of instances, such that T⊆I. Let L be a set of

items, where each item corresponds to an instance or

to a concept of KB. We say that a transaction T

contains X a set of items if X⊆T. Given a set of

transactions , the goal is to find all rules of the form

AÖB, where A and B are disjoint sets of items that

occur in D, and their union satisfy a set of

constraints C

, defined over the ontology O.

Note that this definition differs from the usual

one in two aspects. First, a rule can relate more than

simple objects (instances) and can specify abstract

relations. Second, there is no imposition on the

number of times that A and B occur together. All

depends on the constraints imposed by C

. Indeed,

the first aspect has been neglected, and the user has

to represent the set of transactions at the right

abstraction level. Even in the basket analysis

problem, items do not correspond to real instances

but to some abstraction (when a customer buys a

particular beer and consumes it, other customers

cannot buy it). In the Onto4AR framework, this issue

can be precisely defined by specifying the meaning

of the occurrence of an item in a transaction, outside

the algorithm logic and scope. An item x occurs in a

transaction T if it is equal to some element of T,

where equal is a predicate defined for each concept

on the ontology, and described by some of its

axioms.

ICEIS 2009 - International Conference on Enterprise Information Systems

190

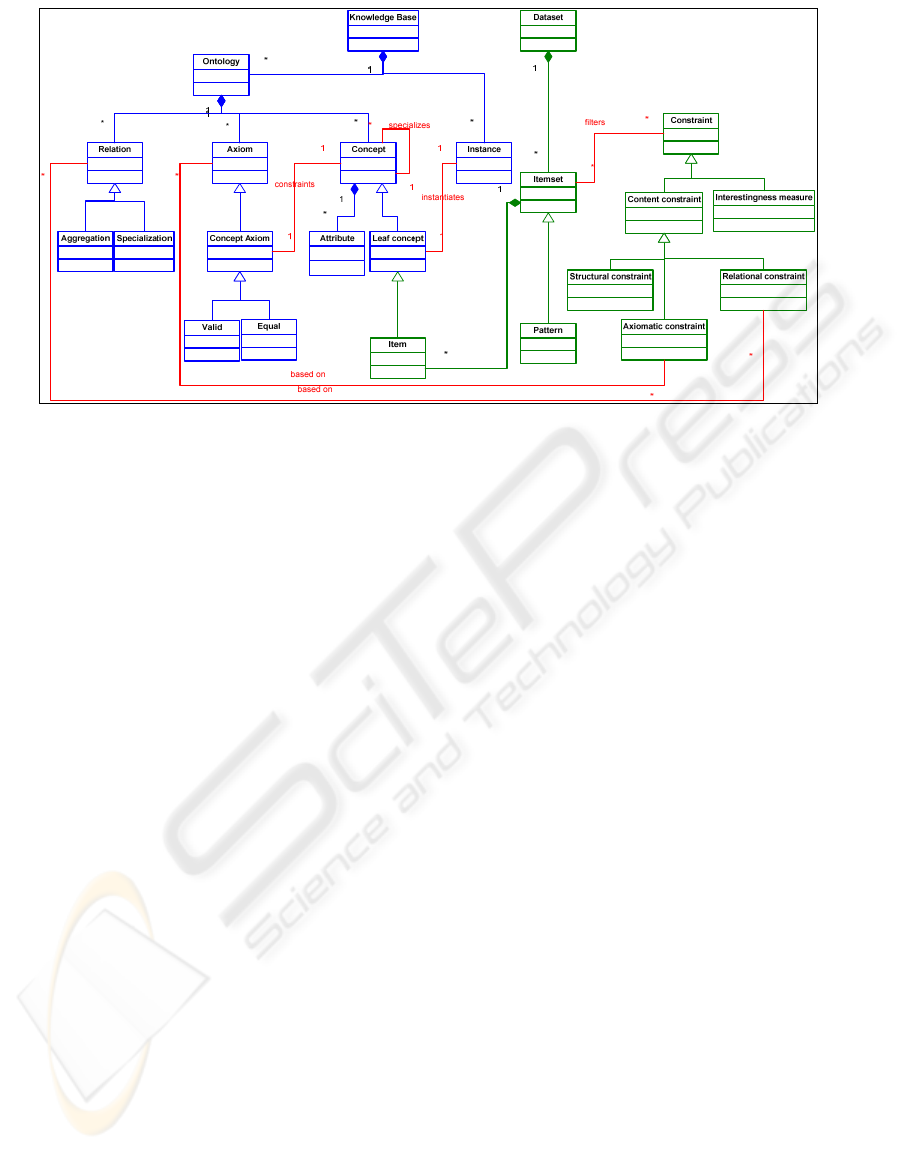
Figure 1 illustrates the framework environment,

defining the relations among the concepts on the

knowledge base/ontology and the concepts in pattern

mining. The figure makes clear that a knowledge

base is composed by an ontology and a set of

instances that instantiate some leaf-concept defined

in the ontology. A leaf concept is just a concept that

has no descendents. It is important to note that

among the axioms defined in the ontology, concept

axioms constraint the characteristics of concepts,

establishing under what conditions they are equal.

In the figure is also clear that a dataset contains a

set of itemsets, which per se are sets of items, and

patterns are particular cases of itemsets (frequent

ones). More interesting is the relation between items

/ itemsets and concepts: an item is a leaf concept and

an itemset corresponds to some concept defined on

the ontology.

The relation between item and concept is the

guarantee that items are defined at the desired level

of abstraction. Indeed, users should only use an

ontology that specialize concepts until the desired

level of abstraction. In addition, equal axiom defined

for each concept establishes the conditions to

consider two items equal or equivalent in accordance

to the domain knowledge. No less relevant is the

valid axiom that allows for restricting the

exploration to valid instantiations. This means that

no itemset that does not have correspondence to any

valid element in the domain is considered in the

exploration.

Finally, in the context of the Onto4AR

framework, a constraint is defined as above. In this

manner, a constraint imposes some condition over

the elements of the itemset, or the relations among

them. These predicates can establish either

qualitative or quantitative conditions. Indeed, at a

first glance, two different categories of constraints

can be distinguished: interestingness constraints

(also known as interestingness measures) and

content constraints.

As seen before, interestingness measures are

constraints that impose quantitative conditions over

the set of items in the rule, like the number of times

that the set of items are transacted together, or the

novelty introduced by the rule. An interestingness

measure is a composed function f=f

[f(x)=g(f

(x))], with g: 2

ÆR and f

: RÆ{true,

false}, defined by the comparison of its argument

with θ, a threshold value.

Although interestingness constraints play a

fundamental role on pattern mining, they only

capture the knowledge about some quantity that is

significant for the specific business. As such, they

are not able to represent any other knowledge about

the business domain. Content constraints introduce

the ability of imposing that items in the rule have

some specific characteristics, which can be selected

among the ones represented in the domain ontology.

A content constraint can be defined as a predicate

: 2

Æ{true, false} that impose some qualitative

condition on the items present in its argument,

expressed based on the domain knowledge

represented in the ontology O.

In the Onto4AR’s context there are several

classes of pre-defined content constraints. Among

them, axiomatic and relational constraints are

defined based on axioms and relations existent on

the ontology. The structural constraint is a particular

case of content constraints and would be defined

later, in the context of the identification of molecular

Figure 1: Problem formulation in the context of a knowledge base

MINING PATTERNS IN THE PRESENCE OF DOMAIN KNOWLEDGE

191

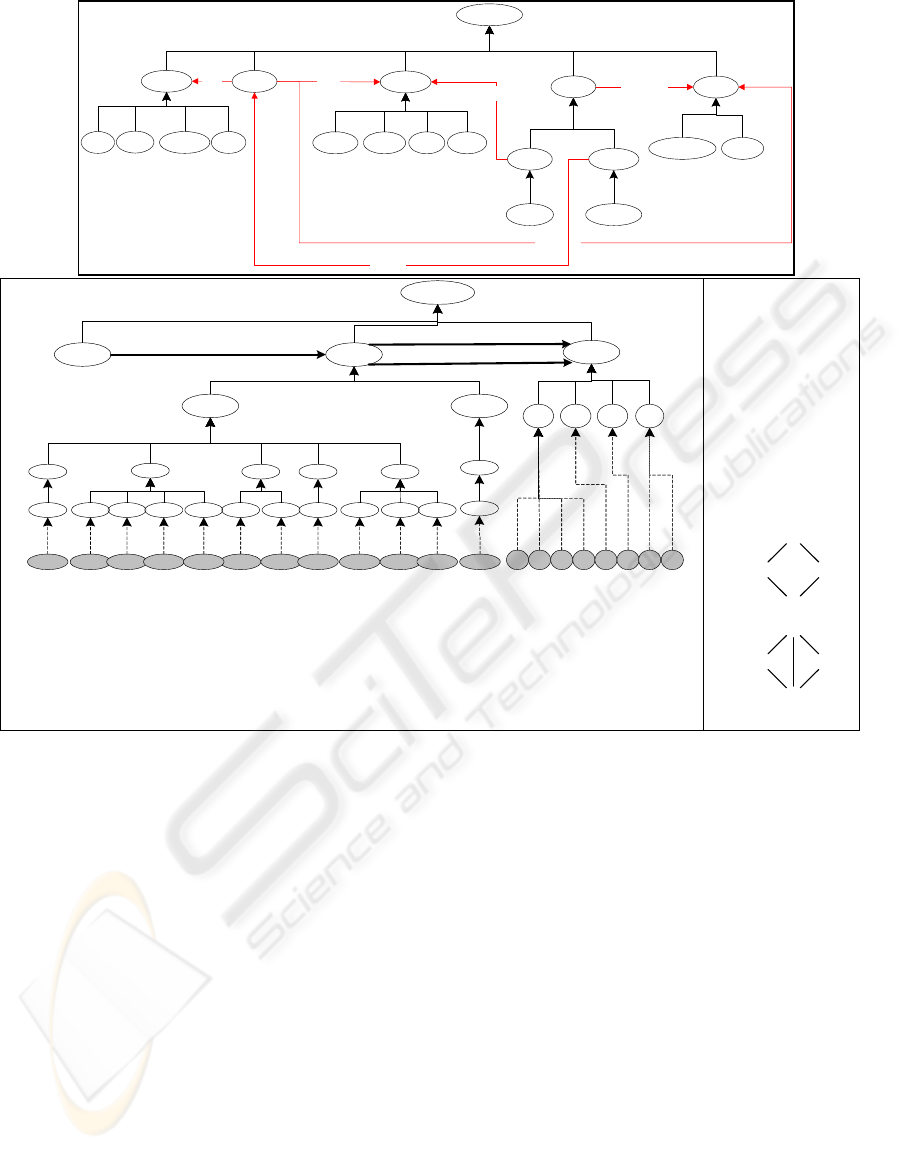
Thing

Action

Category

Hero

Sci-Fi

Thriller

VictimVillain

Western

Role

Actor

Love

interest

Director

Award

Movie

receives

plays

cast

has

Oscar

nomination

Oscar

directs

John

Wayne

George

Lucas

Person

fragments.

Mining in this context can be performed by

OntoCPM algorithm (Antunes2008): an apriori-

based algorithm that acquires domain knowledge

from the knowledge base, instantiates the constraint,

reads the data creating its representation and

identifies frequent patterns. In order to understand

the specificities of this algorithm, some remarks are

needed. First, the candidate generation step is

controlled by the constraint: instead of existing an

unique join operation, there is a join operation for

each specific constraint. In this context, a constraint

is more than a predicate; it is an object, which

implements the predicate itself and other ones such

the areJoinable that verifies if two itemsets can be

joined to generate a new candidate. The second

remark is related to the nature of the constraint. If it

is not anti-monotonic, it is not possible to filter

candidates that have some subset not present in the

previous discovered patterns. In this manner, in this

case, it is not possible to perform neither the anti-

monotonic pruning, and the results of constraint

pruning cannot be used in the next iteration.

4 CASE STUDIES

Consider the movie dataset described in (Widerhold

1989). Among the data, we encounter a description

of the casts, directors and producers for each film.

Additionally, there are some personal and

professional details for each actor. From this dataset,

it is easy to create a knowledge base and ontology,

with equivalent information (Figure 2-top). This

simple ontology states that movies have some

category and a cast, which is composed by several

roles played by actors. Additionally, they are

directed by some people and may receive some

awards. Finally, both actors and people can receive

awards.

Thing

Atom

Double

S=N

Single

Bond

has1st

has2nd

NOS

S-N

-N

S-O

-O

S-C

-C

C-C

-C

C-O

-O

type

atomic-nr

symbol

index

Molecule

bonds

)()i,x(bond),i,x(bond(oconnectedT:)}x(nrBonds,{i)x(valid:Moleculex

)(ndhas.yndhas.xsthas.ysthas.x

ndhas.ysthas.xstthas.yndhas.x)y,x(oconnectedT:Bondsy,x

)()sthas.yndhas.xndhas.ysthas.x

ndhas.y

ndhas.xsthas.ysthas.x(type.ytype.xyx:Bondsy,x

)(symbol.ysymbol.xyx:Atomsy,x

411

32211

2112

21221

2211

+∈∀⇔∈∀

=∨=∨

=∨=⇔∈∀

=∧=∨

=∧=∧=⇔=∈∀

=⇔=∈∀

C — C — S — N

| |

C — C — S — N

C — S — N

C C

N O

Figure 2: Ontology for cinematographic domain (top); knowledge base in chemistry and set of molecular fragments.

ICEIS 2009 - International Conference on Enterprise Information Systems

192

Naturally, categories, movies, roles, actors,

awards and directors are concepts, with categories,

roles and awards specialized by some other

concepts. Relations are represented by directed

arrows. In order to allow the discovery of patterns

involving real actors and directors, the ontology is

enriched with a leaf concept for each known actor

and director. From this ontology and each row in a

denormalized table containing one row for each

participation on a movie, we can construct the

dataset to mine. In order to find patterns in the form

(director, category), (actor, role, category),

(category, award), we only need the axioms that

define equality for each leaf concept.

The identification of frequent molecular

fragments presents additional challenges to the

framework, since those patterns are structured

patterns, in the form of graphs. Allied to this

structural nature, molecules may have multiple

atoms for the same chemical element. In order to

deal with these particularities, the framework only

demands the definition of a new class of constraints

–structural constraints. A structural constraint is a

content constraint that defines a differentiated

areJoinable axiom. It only considers that two

itemsets are joinable if the maximal proper suffix of

the first itemset is equal to the maximal proper

prefix of the second one.

10100

......),(:...,...

−

⇔==∀

nnnn

ttsstseareJoinabltttsss

Note that, this predicate states the new conditions

to generate a candidate, and these conditions are just

the same used by sequential pattern mining

algorithms. For avoiding the problem of the

presence of multiple atoms of the same element, we

can represent a molecule as a chain of bonds, each

one involving two different atoms, as represented in

Figure 2-bottom. This is achieved by representing

each atom as an indexed one, for allowing multiple

identical bonds. For example, the ring of carbons in

Figure 2-bottom (right) would be represented as

–C

). With these simple

tools, it is possible to identify exactly the same

patterns found by graph-mining algorithms.

5 CONCLUSIONS

The recent advances in the area of knowledge

representation makes possible to represent

background knowledge, in an effective way, using

ontologies. Since one of the main drawbacks of data

mining, in general, and of pattern mining, in

particular, is to ignore domain knowledge, with

those advances, it is time to surpass that feature.

This paper explains how the Onto4AR

framework can solve some of the main difficulties

faced by transactional pattern mining approaches,

like dealing with multiple concepts in the same

transaction either on dealing with structured data.

We showed that with the incorporation of

background knowledge in the core of the mining

process, by using domain ontologies and by defining

a set of constraints above them, it is possible to

address those difficulties naturally.

From the case studies described, it is easy to

realize the potentialities of the Onto4AR framework.

Indeed, the framework provides the necessary tools

to overcome several difficulties faced by pattern

mining techniques. Its conception, based on a

standard and widely recognized instrument for

representing existent domain knowledge, is one of

its strongest points, followed closely by its

simplicity and its extensibility.

However, experiments show that candidate-

based algorithms are not the most adequate to

perform the discovery. Definitely, the explosion of

candidates, resulting from the existence of multiple

equivalent concepts (as defined by their equal

predicate), strongly impairs algorithms performance.

However, and since several algorithms following

other approaches have been proposed with a fair

success, it is likely that they can be adapted to

function on this new context.

REFERENCES

Agrawal, R., Imielinsky, T., and Swami, A. Mining

Association Rules between Sets of Items in Large

Databases. In Proc. ACM SIGMOD Conf

Management of Data. 1993. 207-216

Antunes, C., and Oliveira, A.L., Constraint Relaxations for

Discovering Unknown Sequential Patterns. In

Knowledge Discovery in Inductive Databases: Third

International Workshop, Springer, 2005, 11-32

Antunes, C. Onto4AR: a framework for mining

association rules. In Proc. Int’l Workshop on

Constraint-Based Mining and Learning, 2007. 37-48

Antunes, C. An ontology-based method for mining

frequent patterns. Technical report, Instituto Superior

Técnico. 2008.

Bayardo, R.J., The Many Roles of Constraints in Data

Mining. In SIGKDD Explorations, vol. 4, nr. 1 pp. i-ii,

2002.

Garofalakis, M.N., Rastogi, R., and Shim, K., SPIRIT:

Sequential Pattern Mining with Regular Expression

Constraints. In Proc. Very Large Databases Conf.

1999, 223-234

Maedche, A., Ontology Learning for the Semantic Web,

Kluwer Academic Publishers, 2002.

Wiederhold, G., Movies Database Documentation, 1989.

MINING PATTERNS IN THE PRESENCE OF DOMAIN KNOWLEDGE

193