A LOGIC PROGRAMMING FRAMEWORK FOR LEARNING BY

IMITATION

Grazia Bombini, Nicola Di Mauro, Teresa M.A. Basile, Stefano Ferilli and Floriana Esposito

Dipartimento di Informatica, Universit

a degli Studi di Bari, via Orabana 4, Bari, Italy

Keywords:

Learning by imitation, Agents.

Abstract:

Humans use imitation as a mechanism for acquiring knowledge, i.e. they use instructions and/or demonstra-

tions provided by other humans. In this paper we propose a logic programming framework for learning from

imitation in order to make an agent able to learn from relational demonstrations. In particular, demonstra-

tions are received in incremental way and used as training examples while the agent interacts in a stochastic

environment. This logical framework allows to represent domain speciﬁc knowledge as well as to compactly

and declaratively represent complex relational processes. The framework has been implemented and validated

with experiments in simulated agent domains.

1 INTRODUCTION

Learning from demonstration or learning by imita-

tion represents a key research topic in robotics (Bil-

lard and Siegwart, 2004; Schaal, 1999; Schaal et al.,

2003), being a promising approach, based on human-

robot interaction, towards effective robot program-

ming. Indeed, the need of robots that can learn in a

human environment motivates recent research to in-

vestigate forms of social learning, such as imitation-

based learning (Schaal, 1999) and learning by demon-

stration (Nicolescu and Mataric, 2003), inspired by

the way people learn. By means of this approach, a

robot should learn to imitate a teacher by observing

demonstrations. Recent research in other ﬁelds con-

siders imitative learning as an essential part of human

development (Meltzoff, 2007). Humans and animals

use imitation as a mechanism for acquiring knowl-

edge. This method of learning has been shown (Cher-

nova and Veloso, 2007) to reduce learning time com-

pared to classical exploration-based methods such as

reinforcement learning (Smart and Kaelbling, 2002).

Learning from demonstration is an approach that

enables robots (an unskilled agent or the observer)

to learn tasks by simply observing performances of

a skilled agent (the teacher) (Atkeson and Schaal,

1997; Smart and Kaelbling, 2002). The robot gath-

ers information about the task in the form of percep-

tual inputs and action outputs and estimates the latent

control policy of the demonstrator. The estimated pol-

icy can then be used to drive the robots’s autonomous

behavior.

This paper aims at providing a framework that al-

lows an agent to learn and revise in an incremental

way a high level representation of a task by imitating

a skilled agent.

Learning from demonstration is strongly related

to supervised learning, in which the goal is to learn

a policy given a ﬁxed set of labeled data (Bentivegna

et al., 2004). In this perspective it is possible to col-

lect the interaction performed by teaching in the real

world and to use it as examples for the learning phase.

Such examples represent the best action to be taken in

that context. Additionally, data are gathered incre-

mentally, thus minimizing the number of labeled data

required to learn the given policy.

In this paper we present an incremental policy

learning approach based on a relational language used

to describe both the demonstration examples and the

learnt policy. The agent actively interacts with the

human by deciding the next action to execute and re-

questing demonstration from the expert based on the

currently learned policy.

2 LOGICAL BACKGROUND

We used Datalog (Ullman, 1988) as a representation

language for the domain and induced knowledge, that

here is brieﬂy reviewed. For a more comprehen-

sive introduction to Logic Programming and Induc-

tive Logic Programming (ILP) we refer the reader

218

Bombini G., Di Mauro N., M. A. Basile T., Ferilli S. and Esposito F. (2009).

A LOGIC PROGRAMMING FRAMEWORK FOR LEARNING BY IMITATION.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

218-223

DOI: 10.5220/0002007502180223

 SciTePress

to (Bratko, 2001; Muggleton and De Raedt, 1994;

Lavrac and Dzeroski, 1994).

A ﬁrst-order alphabet consists of a set of con-

stants, a set of variables, a set of function symbols,

and a non-empty set of predicate symbols. Each func-

tion symbol and each predicate symbol is associated

to a natural number (its arity). The arity represents

the number of arguments the function has. A term is a

constant symbol, a variable symbol, or an n-ary func-

tion symbol f applied to n terms t

, t

, . . . , t

. An atom

(or atomic formula) p(t

, . . . , t

) is a predicate symbol

p of arity n applied to n terms t

. An atomic formula l,

or its negation l, is said to be a (respectively, positive

or negative) literal.

A clause is a formula of the form

∀X

. . . ∀X

∨ L

∨ . . . ∨ L

∨ L

i+1

∨ . . . ∨ L

)

where each L

is an atom and X

, X

, . . . X

are all

the variables occurring in L

∨ L

∨ . . . L

Most commonly the same clause is written as

an implication L

, L

, . . . L

i−1

← L

, L

i+1

, . . . L

where L

, L

, . . . L

i−1

is the head of the clause and

, L

i+1

, . . . L

is the body of the clause.

Clauses, literals and terms are said to be ground

whenever they do not contain variables. A Datalog

clause is a clause with no function symbols of non-

zero arity; only variables and constants can be used

as predicate arguments.

A substitution θ is deﬁned as a set of bindings

← a

, . . . , X

← a

} where X

, 1 ≤ i ≤ n are vari-

ables and a

, 1 ≤ i ≤ n are terms. A substitution θ is

applicable to an expression e, obtaining the expres-

sion eθ, by replacing all variables X

with their corre-

sponding terms a

3 LEARNING FROM

DEMONSTRATION

Here, we assume that the environment is deﬁned by a

ﬁnite set of states S. For each state s ∈ S, the agent has

available a ﬁnite set of actions A(s) ⊆ A which cause

stochastic state transition, where A is the set of all

the primitive actions. In particular, an action a ∈ A(s)

causes a transition to state s

when executed in state

The agent is assumed to observe a demonstrator

that performs the correct sequence of actions useful

to reach a given goal by starting from an initial state

of the environment. During each training sequence,

the agent records the observation about the environ-

ment and the corresponding action performed by the

demonstrator. An observation o ∈ S is represented by

a set of ground Datalog literals.

Example 1. The following set of literals repre-

sents an observation in a blocks world consisting of

4 blocks (a, b, c and d), where blocks can be on the

ﬂoor or can be stacked on each other. Literal on(X, Y )

denotes that block X is on block Y , and that X and

Y belong to the same stack. { clear(a), on(a, c),

on(c, d), on(d, f), clear(b), on(b, f), block(a), block(b),

block(c), block(d), ﬂoor(f) }.

In this domain, the available actions that can

be performed by the demonstrator are of the

kind move(X, Y ), with X ∈ {a, b, c, d} and Y ∈

{a, b, c, d, f }, X 6= Y .

Each training example, e = {a, o}, consists of an

action a ∈ A selected by the demonstrator and an

observation o ∈ S. Obviously, we assume that the

demonstrator uses a good policy π to achieve the goal.

Hence, the aim of the agent is to learn this hidden

policy π : S → A mapping states (observations) to ac-

tions.

Classical supervised learning is based on an in-

ductive learning method able to generalize from pos-

itive and negative examples labeled by the user. In

the case of imitative learning, the action taken by the

teacher agent may be considered as a positive exam-

ple and all other possible actions as negative exam-

ples. In particular, given a state s, if the teacher takes

action a

∈ A(s), then the observer can assume that a

is a positive example and all other actions a

∈ A(s)

1 ≤ j 6= i ≤ |A(s)| are negative ones. A negative ex-

ample a

is considered reliable until the demonstrator

performs a

in state s. The general process must be

slightly modiﬁed in order to retract this kind of ac-

tion.

Furthermore, the process of imitative learning is

naturally modeled by an agent able to modify its the-

ory in an incremental way, where each new incoming

example may give rise to a theory revision process.

We represent the policy as a set of logical clauses

where the head of the clause represent the action

while the body represents the state. In particular, a

clause represents an action that may be performed in

a given state.

Example 2 . In the blocks world domain a learned

rule may be the following: {move(A, B) :- goal on(D,

E), clear(A), on(A, F), on(D, B), block(D), block(E),

block(A), block(F), ﬂoor(B), not(on(F,B))}

Moving block A on the ﬂoor is a good choice if

block A is on block F, block F is not on the ﬂoor, block

D is on the ﬂoor, and the goal is to put block D on

block E.

A LOGIC PROGRAMMING FRAMEWORK FOR LEARNING BY IMITATION

219

Algorithm 1. Tuning(E,T,M).

Input: E: example; T : theory; M: historical mem-

ory;

1: Add E to M

2: if E is a positive example not covered from T

then

3: generalize(T , E, M)

4: else

5: if E is a negative example covered by T then

6: specialize(T , E, M)

4 RELATIONAL INCREMENTAL

LEARNING

4.1 INTHELEX

INTHELEX (INcremental THeory Learner from EX-

ample) (Esposito et al., 2004) is the learning system

for the induction of ﬁrst-order logic theories from

positive and negative examples exploited in this pa-

per. It learns theories in form of sets of Datalog

clauses, interpreted according the Object Identity (OI

for short) (Semeraro et al., 1996) assumption, accord-

ing to which, within a clause, terms (even variables)

denoted with different symbols must be distinct. It

can learn simultaneously several concepts, possibly

related to each other. It uses a full memory storage

strategy, and therefore retains all the available exam-

ples in a historical memory. A set of examples of the

concepts to be learned is incrementally provided by

an expert. Whenever a new example is taken into ac-

count, it is also stored in the historical memory.

INTHELEX is fully and inherently incremental.

The learning phase can start by taking in input a previ-

ously generated version of the theory or from the ﬁrst

available example and an empty theory. The train-

ing examples are exploited by the system to modify

incorrect hypotheses according to a data-driven strat-

egy. When the theory is not correct with respect to an

example, it is rejected and a process of theory revi-

sion starts. Such a process is based on two inductive

reﬁnement operator, one for generalising deﬁnitions

that reject positive examples (completeness), and the

other for specialising deﬁnitions that explain negative

examples (consistency).

Algorithm 1 reports the procedure used in

INTHELEX for reﬁning a theory. M represents the

set of all positive and negative examples already pro-

cessed, E is the current example to be examined, and

T is the theory learned from the examples in M.

4.2 INTHELEX

As already pointed out, INTHELEX works by tak-

ing into account the examples provided in incremental

way by the expert. In the scenario of an agent acting

in a stochastic world, the correct actions of the agent

may be considered as positive examples in a super-

vised learning task.

In our framework we assume that an agent A aims

at learning to act in a world by imitating an expert

agent E. Hence, each action taken from E in a given

state may be considered as a positive example for A.

All other possible actions in the same state should be

considered as negative examples. In this way A as-

sumes that E acts in a correct way. Given an action-

state pair (a, s) and a set A(s) of possible actions that

can be taken in state s, all other actions in A(s) \ a

is assumed to be negative examples while the expert

agent does not take any of them in the same state s.

When it happens, it is necessary to retract the previ-

ous hypothesized negative example.

Given a goal, each training example e = {a, o} be-

longs to a speciﬁc learning class based on action a.

For each class a theory must be learned in order to be

able to predict the corresponding action to be taken

on unseen observations.

The algorithm starts with an empty theory and an

empty historical memory. The agent observes the se-

quences of actions performed by the demonstrator.

For each timestep the agent tries to classify the ob-

servation (i.e., to predict the corresponding action) by

using its learned model. The set N of all actions that

are allowed in the domain and that the agent can per-

form in a state s, but are not performed by the demon-

strator, are supposed to be negative examples for the

class a (the correct action) in the state s.

The classiﬁcation task returns an action c that is

compared to the correct action a the demonstrator per-

forms. When c does not correspond to the action a a

theory revision is needed. All negative examples for

class a with the same body as o are expunged from

the historical memory. A generalization process of the

current theory against example e, according to ﬁltered

historical memory, starts. At the end of the learning

process, the learned theory T represents the optimal

policy.

5 EXPERIMENTAL RESULTS

The proposed learning framework has been applied

to two domains generally used in the ﬁeld of agent

learning.

ICEIS 2009 - International Conference on Enterprise Information Systems

220

Algorithm 2. IIL.

1: errors ← 0

2: T ←

3: M ←

4: loop

5: (o, a) ← get an observation-action pair

6: N ← {(o, ¬a

)|a

∈ A(o) \ {a}}

7: c ← classify(o,T)

8: if c 6= a then

9: errors++

10: for all e ∈ M do

11: if e is negative for the class a with the

same body as o then

12: M ← M \ {e}

13: generalize( T , a ← o, M)

14: M ← M ∪ {a ← o}

15: for all a

∈ N do

16: if M does not contain the positive example

← o then

17: if c = a

then

18: errors++

19: specialize( T , ¬a

← o, M)

20: M ← M ∪ {a ← o}

5.1 The Predator Prey Environment

The ﬁrst experiment regards the problem of learning

a policy in a domain where a predator should cap-

ture a prey. This stochastic environment consists of a

4x4 grid surrounded by a wall, with a predator and a

prey inside. The predator catches the prey if the prey

comes on the same square as the predator at the end of

its move. The prey moves with random actions, while

the predator follows a good user-deﬁned strategy in

order to capture the prey. Both the predator and the

prey can move in four directions: north, east, south

and west. The action of an agent consists in moving

to the cell immediately adjacent in the selected direc-

tion. In case the target cell is a wall, the agent remains

in the same cell. The two agents move in alternate

turns.

An observation is made up of the agent’s percep-

tion about the cells surrounding it in the four direc-

tions and the cell it occupies. The state of each cell

may be empty, wall or agent. Starting from an initial

state, once captured the prey the sequence of obser-

vations does not restart by placing agents in random

positions, but it continues from the positions of catch.

For example, Figure 1 reports a predator agent

having a wall to the west and the prey to the east.

This observation is represented by the following set

of literals: {north(a, e), south(a, e), east(a, p), west(a,

w), under(a, e)} where a stays for the predator agent,

p for the prey agent, e for empty, and w for wall.

In this example, the positive action taken from the

agent is move north(a), while not(move east(a)) and

not(move south(a)) and not(move west(a)) are wrong

actions.

Figure 1: A sample predator-prey domain. The black circle

represents the predator and the gray circle represents the

prey. The ﬁgure on the right represents the predator agent

percept.

Once ﬁxed the strategy to capture the prey, we

simulated a scenario in which a predator instructs an-

other agent to capture the prey in a minimum number

of a steps. Hence, given an observation, the action

taken from the predator represents a positive training

example, while all other possible actions are supposed

to be negative examples.

We generated 10 sequences of observations. Each

sequence, containing the traces of prey’s captures,

is made up of 322.5 positive and 967.5 negative

observation-action pairs on average. Starting from a

positive instance each alternative action has been hy-

pothesised to be a negative instance.

On all of the 10 sequences the system learned a

theory made up of 9.4 clauses, obtained by 14.8 gen-

eralizations and 2.2 specializations (17 errors) on av-

erage. It is worth noting that, in this domain, 1303

examples are sufﬁcient on average for the system to

learn a good policy. All further examples do not af-

fect the learned policy.

In order to evaluate the behavior of the learning

process, we generated a sequence made up of 1568

observation-action pairs. Figure 2 reports the number

of errors (i.e., a generalization or a specialization re-

quest) the agent made during the learning phase. It

can be noticed that the number of error grows until

the system learns the correct policy (i.e., the learned

classiﬁcation theory). Figure 3 reports the predic-

tive accuracy of the policy learnt by the agent dur-

ing the imitation process on the complete historical

memory made up of the complete set of 1568 positive

observation-action pairs.

5.2 The Blocks World Environment

This domain consists of a surface (ﬂoor) on which

there are four blocks. Blocks may be on the ﬂoor or

one on top of another in a stack. To describe the world

we use relations such as on(a, b), i.e. block a is on

A LOGIC PROGRAMMING FRAMEWORK FOR LEARNING BY IMITATION

221

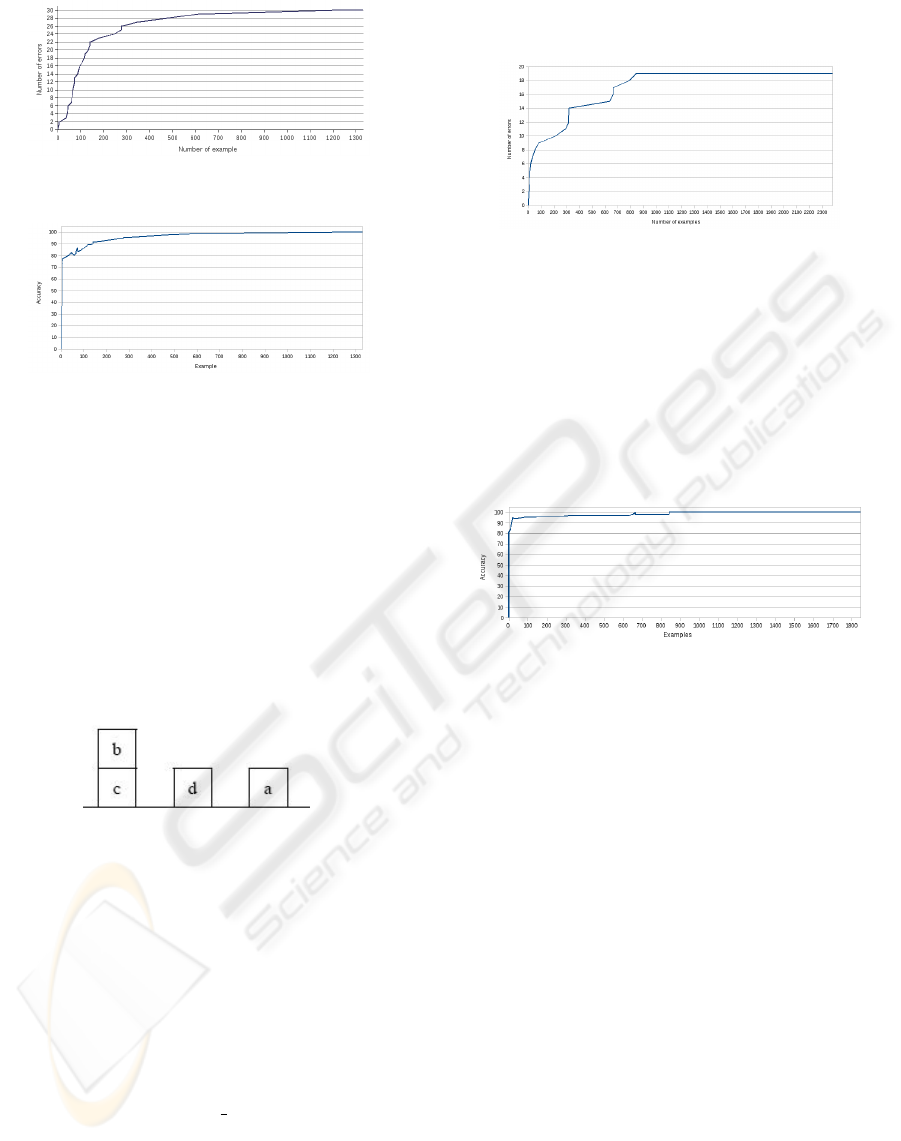
Figure 2: Errors during the learning phase.

Figure 3: Prediction accuracy (%) over the entire historical

memory at each revision theory.

block b, and clear(a), i.e. block a is clear. Only clear

blocks can be moved. An agent can move a block at a

time, on another block or on the ﬂoor. We used the lit-

eral move(a, b) to describe the action of moving block

a on block b.

For example, the conﬁguration reported in Fig-

ure 4 is represented by the following set of literals

{on(c, f), clear(d), on(d, f), clear(a), on(a, f), clear(b),

on(b, c)} where f stas for ﬂoor and a, b, c, d are

blocks.

Figure 4: A blocks world example.

The tasks taken into account are: stack, achieved

when all blocks are on one stack; unstack, achieved

when all blocks are on the ﬂoor; and on(a,b), reached

when block a is on block b. We simulated the be-

havior of an agent able to select effective actions to

achieve a goal (stack, unstack and on(a,b)). Each

observation along with the corresponding action rep-

resents a positive example; all the other actions of

moving other blocks are considered as negative exam-

ples. For instance, considering the scenario reported

in Figure 4, if the goal is goal on(a, b), the correct ac-

tion is move(a, b) and the wrong actions are move(a,

d), move(b, f), move(b, d), move(b, a), move(d, a),

move(d, b).

We have generated 10 sequences of observations.

Each sequence is made up on average of 382.1 pos-

itive observation-action pairs, and 2055.2 negative

observation-action pairs generated starting from the

positive action.

Figure 5: Errors during the learning phase.

Figure 5 reports the number of errors the agent

made during the learning phase on a sequence of 2379

observation-action pairs.

On all of the 10 sequences the system learned a

theory made up of 5.2 clauses, obtained by 5.8 gen-

eralization and 3.1 specialization (8.2 errors) on aver-

age. It is worth noting that, in this domain, 821 exam-

ples on average are sufﬁcient for the system to learn a

good policy.

Figure 6: Prediction accuracy (%) over the entire historical

memory at each revision theory.

Figure 6 reports the predictive accuracy of the

agent on the historical memory at the and of the learn-

ing process.

6 CONCLUSIONS AND RELATED

WORKS

An agent can learn using real examples of agent in-

teraction with the world. In (Jebara and Pentland,

2002) the distribution of the environment is used to

predict an agent’s behavior. (Verma and Rao, 2007)

proposes a framework for imitative learning that uses

a probabilistic Graphical Model to describe an imita-

tion process. A Graphical model is used to model the

behavior of both the agent and the observed teacher.

In (Jansen and Belpaeme, 2006) the authors

present a model for ﬁnding the intended goal of a

demonstration using iterative interactions. They in-

fer the goal of a demonstration without imitating the

steps on how to reach the goal, but based on some

psychological observations reported in (Wohlschlager

et al., 2003). The same psychological observations

ICEIS 2009 - International Conference on Enterprise Information Systems

222

are taken into account in (Billard et al., 2004), in

which agents learn new goals and how to achieve

them.

In (Chernova and Veloso, 2007) a demonstration-

based learning algorithm (conﬁdent execution frame-

work) is used to train an agent. Such a framework al-

lows an agent to learn a policy from demonstration. In

the learning process, the agent observes the execution

of an action. An agent is provided with a decision-

making mechanism that allows it to actively choose

whether observing or acting, with a gradually increas-

ing autonomy. To learn a policy a supervised learning

approach is used and the training data are acquired

from the demonstration. All these approaches still do

not use a relational representation formalism able to

generalize the learned policies.

In this paper we have presented a logic framework

that allows quickly, incrementally and accurately to

train an agent to imitate a demonstrator of the task.

REFERENCES

Atkeson, C. and Schaal, S. (1997). Robot learning from

demonstration. In Fisher, D., editor, Proceedings of

the 14th International Conference on Machine Learn-

ing (ICML), pages 12–20.

Bentivegna, D., Atkeson, C., and Cheng, G. (2004). Learn-

ing from observation and practice using primitives. In

AAAI Fall Symposium Series, ‘Symposium on Real-

life Reinforcement Learning’.

Billard, A., Epars, Y., Calinon, S., Cheng, G., and Schaal,

S. (2004). Discovering Optimal Imitation Strate-

gies. robotics and autonomous systems, Special Issue:

Robot Learning from Demonstration, 47(2-3):69–77.

Billard, A. and Siegwart, R. (2004). Robot learning from

demonstration. Robotics and Autonomous Systems,

47(2-3):65–67.

Bratko, I. (2001). Prolog programming for artiﬁcial intelli-

gence, 3rd ed. Addison-Wesley Longman Publishing

Co.

Chernova, S. and Veloso, M. (2007). Conﬁdence-based pol-

icy learning from demonstration using gaussian mix-

ture models. In AAMAS ’07: Proceedings of the 6th

international joint conference on Autonomous agents

and multiagent systems, pages 1–8, New York, NY,

USA. ACM.

Esposito, F., Ferilli, S., Fanizzi, N., Basile, T., and

Di Mauro, N. (2004). Incremental learning and con-

cept drift in inthelex. Intelligent Data Analysis Jour-

nal, Special Issue on Incremental Learning Systems

Capable of Dealing with Concept Drift, 8(3):213–237.

Jansen, B. and Belpaeme, T. (2006). A computational

model of intention reading in imitation. Robotics and

Autonomous Systems, 54(5):394–402.

Jebara, T. and Pentland, A. (2002). Statistical imitative

learning from perceptual data. In Proc. ICDL 02,

pages 191–196.

Lavrac, N. and Dzeroski, S. (1994). Inductive Logic Pro-

gramming: Techniques and Applications. Ellis Hor-

wood, New York.

Meltzoff, A. N. (2007). The ”like me” framework for recog-

nizing and becoming an intentional agent. Acta Psy-

chologica, 124(1):26–43.

Muggleton, S. and De Raedt, L. (1994). Inductive logic

programming: Theory and methods. Journal of Logic

Programming, 19/20:629–679.

Nicolescu, M. N. and Mataric, M. J. (2003). Natural meth-

ods for robot task learning: instructive demonstra-

tions, generalization and practice. In Proceedings

of the second international joint conference on Au-

tonomous agents and multiagent systems (AAMAS03),

pages 241–248. ACM.

Schaal, S. (1999). Is imitation learning the route to

humanoid robots? Trends in cognitive sciences,

3(6):233–242.

Schaal, S., Ijspeert, A., and Billard, A. (2003). Com-

putational approaches to motor learning by imita-

tion. Philosophical Transactions: Biological Sci-

ences, 358(1431):537–547.

Semeraro, G., Esposito, F., and Malerba, D. (1996). Ideal

reﬁnement of datalog programs. In Proietti, M., editor,

Logic Program Synthesis and Transformation, volume

1048 of LNCS, pages 120–136. Springer.

Smart, W. and Kaelbling, L. (2002). Effective rein-

forcement learning for mobile robots. In IEEE In-

ternational Conference on Robotics and Automation

(ICRA), volume 4, pages 3404–3410.

Ullman, J. (1988). Principles of Database and Knowledge-

Base Systems, volume I. Computer Science Press.

Verma, D. and Rao, R. P. N. (2007). Imitation learning us-

ing graphical models. In Kok, J. N., Koronacki, J.,

de M

antaras, R. L., Matwin, S., Mladenic, D., and

Skowron, A., editors, 18th European Conference on

Machine Learning, volume 4701 of LNCS, pages 757–

764. Springer.

Wohlschlager, A., Gattis, M., and Bekkering, H. (2003).

Action generation and action perception in imitation:

An instantiation of the ideomotor principle. Philo-

sophical Transaction of the Royal Society of London:

Biological Sciences 358, 1431:501–515.

A LOGIC PROGRAMMING FRAMEWORK FOR LEARNING BY IMITATION

223