TOWARDS A UNIFIED STRATEGY FOR THE PREPROCESSING

STEP IN DATA MINING

Camelia Vidrighin Bratu and Rodica Potolea

Computer Science Department, Technical University of Cluj-Napoca, Baritiu St., Cluj-Napoca, Romania

Keywords: Preprocessing, Unified Methodology, Feature Selection, Data Imputation.

Abstract: Data-related issues represent the main obstacle in obtaining a high quality data mining process. Existing

strategies for preprocessing the available data usually focus on a single aspect, such as incompleteness, or

dimensionality, or filtering out “harmful” attributes, etc. In this paper we propose a unified methodology for

data preprocessing, which considers several aspects at the same time. The novelty of the approach consists

in enhancing the data imputation step with information from the feature selection step, and performing both

operations jointly, as two phases in the same activity. The methodology performs data imputation only on

the attributes which are optimal for the class (from the feature selection point of view). Imputation is

performed using machine learning methods. When imputing values for a given attribute, the optimal subset

(of features) for that attribute is considered. The methodology is not restricted to the use of a particular

technique, but can be applied using any existing data imputation and feature selection methods.

1 INTRODUCTION

Machine learning has become one of the main

sources of learning techniques in data mining.

During the last years a great number of state-of-the-

art methods have emerged, while older methods

have been improved. Thus, data mining researchers

possess a rich collection of robust techniques which

tackle the learning phase in the knowledge

extraction process.

Despite the strength of existing learning schemes, on

some problems they fail to achieve a satisfying

performance. The reason behind such a behaviour

can be found in the quality of the training data.

In this paper we propose a generic preprocessing

methodology, which combines feature selection with

data imputation, to improve the quality of the

training data. The end goal is to obtain an increased

learning accuracy.

The rest of the paper is organized as follows: some

of the most common data-related issues are

discussed in section 2. A data imputation and a

wrapper feature selection approach are discussed in

the first part of section 3, followed by the proposed

preprocessing methodology. Section 4 presents the

evaluations performed using two different

implementations of the methodology, followed by

the conclusion section.

2 WHY WE NEED

PREPROCESSING

One of the main issues involved in the learning step

is algorithm selection and engineering. This usually

implies the choice of the “right” algorithm for the

given problem, together with parameter tuning. The

“right” algorithm, in theory, is the one which

matches the problem bias, e.g. the separation hyper-

planes it can learn match the data separation into

classes. Algorithm selection and engineering are

empirical-intensive activities, since many

combinations need to be considered.

Practical experience has shown us that the success of

the mining process does not always depend on the

choice and engineering of the learning technique

alone. An important factor can be found in the

quality of the training data which is presented to the

algorithm. There are several dimensions to this

problem that need to be addressed. Some of the most

common are:

• Data volume (number of instances)

• Incompleteness

• Irrelevant/redundant information

• Dimensionality (number of features/

attributes)

Even tough data mining has emerged from the need

of analyzing large amounts of data, there are some

230

Vidrighin Bratu C. and Potolea R. (2009).

TOWARDS A UNIFIED STRATEGY FOR THE PREPROCESSING STEP IN DATA MINING.

In Proceedings of the 11th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

230-235

DOI: 10.5220/0002008902300235

 SciTePress

cases where the data volume is insufficient for

modelling the true hidden hypothesis.

Incomplete data has proved to be the rule, rather

than the exception of a data mining process.

Incomplete datasets could result from many causes,

such as: the values are out of the range of the

measuring device, may signal a don’t care value, is

the result of a random event, a.s.o. Incomplete

datasets usually bias the learning step, even for

techniques which are able to learn from incomplete

data. Although there exists a taxonomy for data

incompleteness (Little & Rubin, 1987), with

systematic and efficient approaches for dealing with

each type of incompleteness, this issue is neither

trivial nor easy to handle. The main difficulty is that

the type of incompleteness is, in most cases,

unknown, rendering impossible the choice of the

appropriate technique. This makes its treatment

more challenging, since informative missing values

should be handled differently than random

incompleteness.

Supposing that for a given problem the “right”

classifier has been identified, the monotonic

assumption – that more attributes improve the

learning phase – is not generally valid. This is due to

the irrelevant/redundant information in the data,

which harms the learning process. This suggests

that, theoretically, the data should be cleaned and

only strongly relevant attributes should be preserved.

In practice, however, the strongly relevant attributes

(as defined by theory) are hard to establish.

Furthermore, in some cases, data which is

theoretically redundant may enhance the learning

process (e.g. adding the product of the two variables

in an XOR problem improves the accuracy of a

neural network classifier, (Georgieva, 2008)).

High dimensionality (i.e. a very large number of

attributes) has also other implications than the

inclusion of irrelevant/redundant information. It

usually results in slow learning and a complex and

difficult to interpret output model.

This list of data-related problems we have

enumerated is far from exhaustive, but we consider

that finding viable, widely-applicable solutions to

these issues is the first step to improving the data

mining process. Starting from these facts, we have

explored a data imputation and a wrapper feature

selection strategy, and performed evaluations on

benchmark data. The aim was to obtain a better

accuracy after the learning process. Starting from the

results obtained, we propose a combined

preprocessing methodology for the data mining

process. The final goal is to provide general

approaches to handle different data-related problems

in a unified manner.

3 PRE-PREOCESSING

APPROACHES

We have come across the need to employing more

elaborate preprocessing strategies while mining a

prostate cancer dataset using complex classification

approaches. On medical benchmark data, the

complex techniques obtained the best/at least similar

results when compared to prominent learning

techniques existing in literature (Vidrighin et. al,

2007), in terms of classification accuracy or total

cost. On a real prostate cancer dataset the

performance of the techniques remained at the

highest level when compared to the performance of

the same “competition” approaches. However, due

to the sensitivity of this particular domain, the

accuracy obtained is considered to be insufficiently

high. Since the other techniques employed have

failed to obtain a better accuracy, we have started to

search for a preprocessing solution in order to boost

the classification accuracy. A first approach started

from the observation that the prostate cancer dataset

contains a lot of missing values. Thus, we focused

on methods for imputing the missing values. Also,

even though in this case the data dimensionality is

not an issue, we have employed a wrapper

methodology to identify the optimal predictive

subset for the problem. Given the domain

particularities, this leads to a better model

interpretability and also eliminates harmful

irrelevant/redundant information, hence reducing the

medical costs.

3.1 Data Imputation

Our method for data imputation is inspired from

machine learning techniques. We found motivation

in the increased accuracy rates obtained by an

ensemble of artificial neural networks on various

benchmark datasets. The technique involves training

the ensemble on the available complete data for a

given attribute. For each predictor attribute A

, i=1,n,

we split the training set T into the training subset of

complete data and the training subset of incomplete

data: T = CT

+ IT

. Given the attribute A

and an

instance t∈T, t∈CT

if the value of A

is present and

t∈IT

otherwise. The ensemble of neural networks is

trained on CT

, considering A

as the class, and the

obtained model is employed to impute the values for

in IT

, resulting in IT

’.

The resulting training set IT’ = CT

+ IT

’ should

have a higher quality, and thus improve the learning

phase.

TOWARDS A UNIFIED STRATEGY FOR THE PREPROCESSING STEP IN DATA MINING

231

We have performed evaluations considering several

different ratios of incompleteness. We have

measured the classification accuracy of a decision

tree learner. For each attribute we have compared

results using three variants of the training set:

• complete training set: IT

= ∅, T = CT

• incomplete: p% of the attribute values are

considered missing, with p between 5 and 30,

with a 5% increment

• imputed: p% of the attribute values have been

imputed by our method (p the same as before)

The evaluations were performed in a 10-fold cross

validation loop (for the training/testing sets), 10

times for each incompleteness percentage, using

different splits every time (for the training set).

The results suggest that the method could be used to

improve the quality of the training set. The

observations can be divided into three categories,

considering each attribute’s correlation with the

class (measured using the gain ratio): highly

correlated attributes, mildly correlated attributes and

weakly correlated attributes. The most stable

improvements have been found for attributes which

possessed a strong correlation with the class and for

datasets with increased modelling power (measured

in terms of the classification accuracy level) –

(Vidrighin et. al, 2008a). This result, together with

the fact that the optimal subset contains the strongly

relevant features, indicates the possibility of

augmenting the mining process with a combined

approach for preprocessing.

3.2 Wrapper Feature Selection

We have defined feature selection as the process of

selecting the optimal subset of features for a dataset.

Optimality may refer to: improving the classification

accuracy, reducing the computation effort,

improving model interpretability or avoiding costly

features. Our target is to achieve the highest possible

accuracy.

We have employed a 3-step methodology, based on

an existing classification for feature selection

methods (Kohavi, 1997). Therefore, we view the

wrapper as a 3-tuple of the form <generation

procedure, evaluation function, validation function>.

The generation procedure is a search procedure

which selects a subset of features (F

) from the

original feature set (F), F

⊆ F. There are many

search methods available, from greedy hill climbing

search, to genetic or random search methods. Each

has its advantages and disadvantages. Previous work

(Vidrighin et. al, 2008b) has shown that greedy

stepwise backward search and best first search

constantly yield good results. We have employed

these two search methods as generation procedures

in our previous evaluations (Vidrighin et. al, 2008c).

The evaluation function measures the “quality” of a

subset obtained from a given generation procedure.

As the optimal features subset depends on the

evaluation function, the process of selecting the

appropriate evaluation function is dependent on the

particular initial dataset. In the case of wrappers, the

evaluation is performed by measuring the accuracy

of a certain inducer on the projection of the initial

dataset on the selected attributes. In our previous

work we have employed three different learning

schemes (inducers), representing three prominent

classes of algorithms: decision trees (C4.5 – revision

8 – J4.8, as implemented by Weka (Witten, 2005));

Naïve Bayes (Cheeseman & Stutz, 1995) and

ensemble methods (AdaBoost.M1 (Freund &

Schapire, 1997)). For J4.8, we performed

experiments both with and without pruning.

The validation function tests the validity of the

selected subset through comparisons obtained from

other feature selection and generation procedure

pairs. The objective of the validation procedure is to

identify the best performance that could be obtained

in the first two steps of the method for a given

dataset, i.e. to identify the selection method which is

most suitable for the given dataset and classification

method. In this phase we performed validations with

all the three inducers employed in the evaluation

phase. Again, J4.8 was considered both with pruning

and without pruning. Validation is important in

selecting the inducer for learning after feature

selection has been performed.

Evaluations on 11 benchmark datasets (Vidrighin et.

al, 2008c) have shown that feature selection almost

always improves the accuracy of any inducer. The

most were found for combinations which included

the Naïve Bayes classifier, but J4.8 combination also

obtained good improvements. The best wrapper

combinations obtained up to 13% relative

improvements in accuracy (when compared to the

initial accuracy of the inducer), while the second

best obtained up to 7% relative improvements. Also,

combinations using the initially best inducer for

evaluation and validation have obtained relative

improvements in accuracy up to 7%. Therefore,

employing the reduced optimal feature set rather

than the initial set almost always boosts the learning

accuracy. For datasets having over 99% accuracy no

improvement has been found.

3.3 A Combined Strategy

Starting from the results obtained by both

preprocessing approaches explored, we propose a

ICEIS 2009 - International Conference on Enterprise Information Systems

232

unified strategy for preprocessing the data, which

consists in two phases:

• a feature selection phase

• a data imputation phase

The novelty of the approach consists in enhancing

the data imputation step with information from the

feature selection step, and performing both

operations jointly, as two phases in the same

activity.

In the feature selection phase, we extract the class

optimal feature subset (further referred as COS), i.e.

the subset of features which best predicts the class.

We have employed classification accuracy as

optimality criterion. Also, for each attribute, A

, in

the optimal subset, we perform feature selection on

the entire training set, to obtain its optimal subset,

AOS

. The optimality criterion should be accuracy

here as well, but the methodology does not impose

the use of a given method (e.g. filter ranking

methods could be employed instead of wrappers).

In the data imputation phase we impute values for

the incomplete attributes in the optimal subset of the

class. For each attribute we will consider only the

features in its optimal subset, AOS

for imputation.

By performing feature selection for each attribute in

particular, we wish to eliminate any noise and

harmful information.

After imputation, the resulting training set represents

the improved training set, which is further used in

the learning step.

This is a simple, generic strategy, which can be

applied using any feature selection and data

imputation techniques. It is neither restricted to

wrapper feature selection in the feature selection

phase, nor to a particular imputation method.

The next section presents the evaluations performed

on two particular implementations of the

methodology.

4 EVALUATIONS

We have performed evaluations using complete

benchmark datasets from the UCI Machine Learning

Data Repository (UCI), to check whether the

imputation-feature selection combination can

improve the accuracy of a classifier. We have

experimented with two particularizations of the

methodology: one that employs an ensemble of

artificial neural networks for imputation, and one

that utilizes kNN for imputation. Both strategies

employ a wrapper method for feature selection.

4.1 Preprocessing with Ensembles of

Artificial Neural Networks for

Imputation

The first set of evaluations has been performed on a

variant of the preprocessing methodology which

utilizes the data imputation technique and the feature

selection method already explored in (Vidrighin et.

al, 2008a) and (Vidrighin et. al, 2008c).

The evaluation methodology is as follows:

1. select the best wrapper method for the

given dataset

2. generate 10 random train/test sets pairs

(from the original dataset), using a 80/20

percentage split.

3. for each training set, select the optimal

feature subset (for the class attribute), using

the wrapper method selected at 1.

4. for each training set, evaluate the

imputation technique, as described in

section 3.1

In step 3 of the evaluation methodology we have not

considered the optimal attribute subset for each

attribute separately, AOS

. Instead, we used COS for

attribute imputation as well. This may lead to poorer

results, since the attributes in COS are not

necessarily predictive among each other. Therefore,

when imputing values for attribute A

, only the

features in its optimal subset should be employed.

Also, for each training/testing pairs, COS has been

estimated on the complete training set, without

taking into account any missing values. In a real

world setting this should also have a different

approach: either perform feature selection on CT

for each attribute A

, or consider incompleteness in

the evaluation function of the feature selection

technique.

Table 1 presents the average classification

accuracies obtained by training a multilayer

perceptron classifier on different versions of the

training set with respect to attribute GlucTest:

preprocessed with the combined methodology,

incomplete, and original complete set. GlucTest has

been selected in COS as being strongly correlated

with the class and imputation has been performed on

= GlucTest, when AOS

= COS.

The improvement does not seem to be significant,

but we believe this is due to the fact that we

employed COS for imputing the values of A

, and

not AOS

. Also, we consider that a more stable

approach than artificial neural networks for data

imputation would yield better results.

TOWARDS A UNIFIED STRATEGY FOR THE PREPROCESSING STEP IN DATA MINING

233

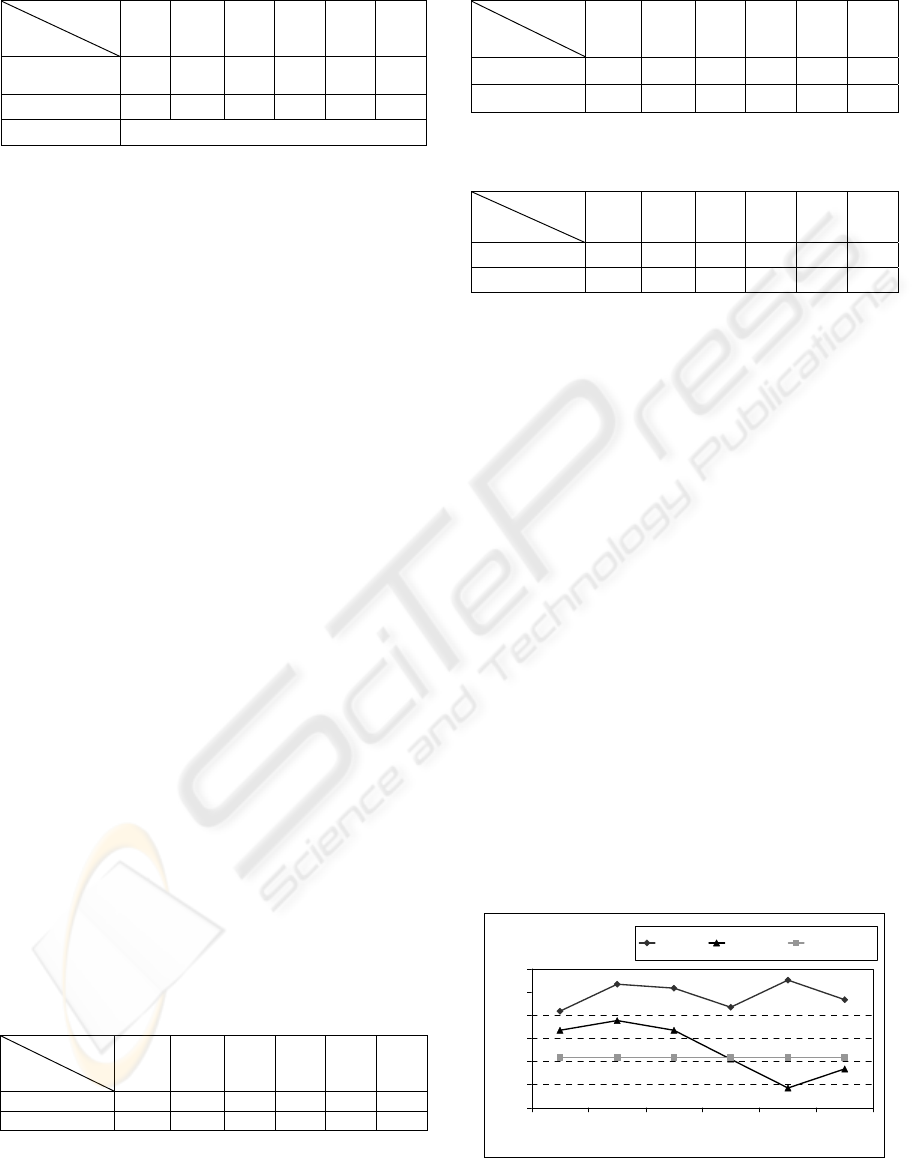
Table 1: Classification accuracies for different versions of

the training set for attribute GlucTest, Pima dataset.

%incomplete

accuracy

5% 10% 15% 20% 25% 30%

Pre-processed

(combined m.)

76.5 76.47 76.45 76.42 76.43 76.32

Incomplete

76.46 76.45 76.49 76.34 76.26 76.45

Original data

76.58

4.2 Preprocessing with kNN for

Imputation

For evaluating this second approach we have

employed the following datasets: Cleveland, Bupa,

Pima and Cars. Two slightly different strategies

have been considered:

• In the first one (FSAfterI), for each attribute A

in the training set (except the class) we have

varied the percentage of incompleteness

between 5% and 30%, with 5% increment. To

impute the missing values for A

, we have

employed kNN, k=3, using only the attributes

in AOS

(computed using a wrapper approach

around kNN). The final classification was

performed using J4.8, on COS (computed using

a wrapper approach around J4.8).

• In the second approach (FSBeforeI), COS was

computed initially, and only the attributes in

COS were considered for imputation. In order

to impute values for A

, AOS

, was extracted

from the original training set.

A stratified 10-fold cross validation was performed

for each experiment. The average classification

accuracy and the standard deviation were computed.

In the trials of the second strategy, for each attribute

, averaging was performed only on the folds in

which it was selected in COS. We have compared

the accuracy of the model built using J4.8 on the

entire training set against the accuracy of the model

built on the pre-processed training set.

Tables 2-4 present the results obtained on the Pima

dataset, for a strongly correlated attribute (with the

class), a mildly and a weakly correlated attribute.

Table 2: Results of a strongly correlated attribute with the

class, Pima dataset (GlucTest).

%incomplete

accuracy

5% 10% 15% 20% 25% 30%

FSAfterI

74.74 74.08 75.39 74.21 74.08 75.13

FSBeforeI

73.16 74.08 73.29 74.08 72.24 73.29

Table 3: Results of a mildly correlated attribute with the

class, Pima dataset (Age).

%incomplete

accuracy

5% 10% 15% 20% 25% 30%

FSAfterI

73.95 73.95 74.61 74.47 75 72.89

FSBeforeI

76.32 75.26 74.47 75.26 76.05 73.42

Table 4: Results of a weakly correlated attribute with the

class, Pima dataset (BloodPress).

%incomplete

accuracy

5% 10% 15% 20% 25% 30%

FSAfterI

74.21 74.21 73.82 74.21 73.16 73.55

FSBeforeI

72.63 72.63 71.84 72.11 72.11 72.11

We have compared the accuracy of the final

classification with J4.8 on the complete set (74.74%)

with its performance on the modified training sets

obtained through preprocessing with the two

versions of the proposed methodology (FSAfterI and

FSBeforeI). Good results can be observed for

strongly and mildly correlated attributes. There is no

clear winner between the two approaches, and no

success pattern can be identified.

The most remarkable improvements have been

observed on the Cleveland data set, whose baseline

accuracy lies somewhere around 50%. Figures 1-2

exemplify the results obtained for a strongly and a

mildly correlated attribute with the class in the

Cleveland data set. The combined preprocessing

technique significantly boosts the performance of

the model built on the pre-processed training set

when compared to the performance of the model

built on the original training set. For this dataset in

particular, FSAfterI yields better results than

FSBeforeI, for all attributes.

The results obtained on the other two datasets

confirm the fact that preprocessing the training set

using this combined methodology can help boost the

classification accuracy. Also, there appears to be no

absolute winner between the approaches.

Figure 1: Classification accuracy using different versions

of the training set – attribute Thal.

Cleveland Dataset

Attribute Thal

5% 10% 15% 20% 25% 30%

% incomplete

accuracy (%)

FSAfterI FSBeforeI Original data

ICEIS 2009 - International Conference on Enterprise Information Systems

234

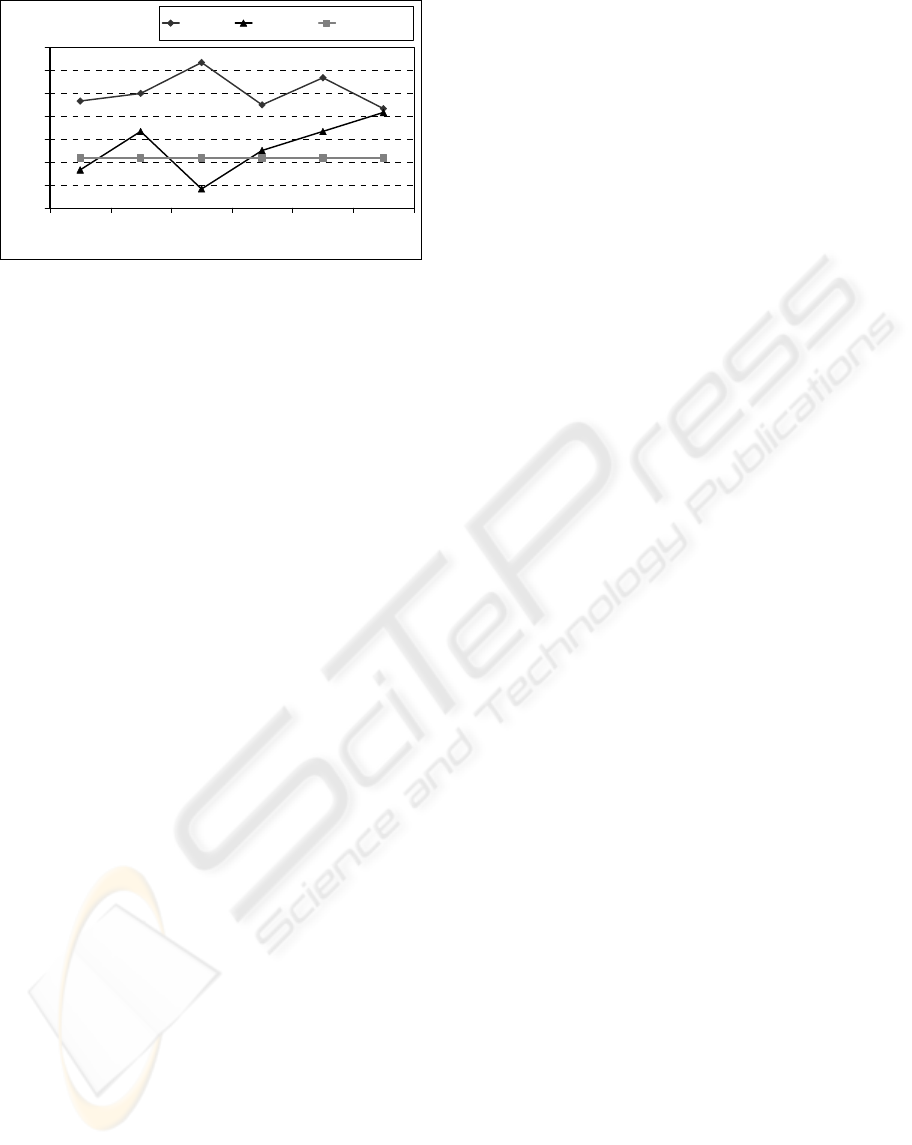
Figure 2: Classification accuracy using different versions

of the training set – attribute MaxHeartRate.

5 CONCLUSIONS

Among the best known data preprocessing strategies

are feature selection and procedures for handling

incomplete data, with various existing techniques.

Previous results on the data imputation step alone

show that predicting strongly correlated attributes

with the class can improve the learning accuracy.

Wrapper feature selection has also been shown to

boost the performance of an inducer.

In this paper we propose a new methodology for

preprocessing the training set. Its novelty resides in

the combination of the feature selection step with

data imputation, in order to obtain an improved

version of the training set. The main goal is to boost

the classification accuracy (i.e. improve the learning

step). The methodology is simple and generic, which

makes it suitable for a wide range of application

domains, where particular feature selection schemes

/data imputation procedures may be preferred.

We have performed a number of evaluations of the

combined methodology using benchmark datasets.

The results indicate that performing preprocessing

on the training set enhances the accuracy of the final

model. The new methodology we have introduced is

more successful than the individual steps it

combines, producing similar or even superior results

to the ones obtained with complete data.

However, just like in the case of classifiers

(Moldovan et. al, 2007), there is no absolute best

preprocessing particularization for a given dataset.

Therefore, there appears the need to assess a

baseline performance using several approaches, and

develop a semi-automated procedure for tuning the

preprocessing method for a given problem. This is

one of our current objectives. Another future

development of the methodology is aimed at

handling more complex patterns of incompleteness,

closer to the ones encountered in real-life data sets.

ACKNOWLEDGEMENTS

Our work for this paper has been supported by the

Romanian Ministry for Education and Research,

through grant no. 12080/01.10.2008 – SEArCH.

REFERENCES

Cheeseman, P., Stutz, J., 1995. “Bayesian classification

(AutoClass): Theory and results”, Advances in

Knowledge Discovery and Data Mining. Menlo Park,

CA: AAAI Press, pp. 153–180.

Freund, Y., Schapire, R., 1997. “A decision-theoretic

generalization of on-line learning and an application to

boosting”, Journal of Computer and System Sciences,

55(1):119–139

Georgieva, P., 2008. “MLP and RBF algorithms”, Summer

School on Neural Networks and Support Vector

Machines, Porto, 7-11 July.

Hall, M.A., 2000. Correlation based Feature Selection for

Machine Learning. Doctoral dissertation, Department

of Computer Science, The University of Waikato,

Hamilton, New Zealand.

Kohavi R., John, J. H., 1997, “Wrappers for feature subset

selection”, Artificial Intelligence, Volume 7, Issue 1-2.

Little, R.J.A., Rubin, D.B., 1987. Statistical Analysis with

Missing Data, J. Wiley & Sons, New York.

Moldovan, T., Vidrighin, B.C., Giurgiu, I. and Potolea, R.,

2007. "Evidence Combination for Baseline Accuracy

Determination". Proceedings of the 3rd ICCP 2007,

Cluj-Napoca, Romania, pp. 41-48.

Nilsson, R., 2007. Statistical Feature Selection, with

Applications in Life Science, PhD Thesis, Linkoping

University.

UCI Machine Learning Data Repository,

http://archive.ics.uci.edu/ml/ , last accessed Dec. 2008

Vidrighin, B.C., Potolea, R., Petrut, B., 2007. "New

Complex Approaches for Mining Medical Data",

Proc. of the WCMD, ICCP 2007, pp 1-10.

Vidrighin, B. C., Muresan, T., Potolea, R., 2008a.

“Improving Classification Performance on Real Data

through Imputation”, Proc. of the 2008 IEEE AQTR,

Romania, Vol. 3, pp. 464-469.

Vidrighin, B. C, Potolea, R., 2008b. “Towards a

Combined Approach to Feature Selection”, In Proc. of

the 3

ICSOFT 2008, Porto, Portugal.

Vidrighin, B. C., Muresan, T., Potolea, R., 2008c.

“Improving Classification Accuracy through Feature

Selection”, Proc. of the 4

IEEE ICCP 2008, pp 25-32

Witten, I., Frank E., 2005. Data Mining: Practical

machine learning tools and techniques, 2

edition,

Morgan Kaufmann.

Cleveland Dataset

Attribute MaxHeartRate

5% 10% 15% 20% 25% 30%

% incomplete

accuracy (%)

FSAfterI FSBeforeI Original data

TOWARDS A UNIFIED STRATEGY FOR THE PREPROCESSING STEP IN DATA MINING

235