AN APPLICATION OF THE SPECTRAL KURTOSIS TO MONITOR

CONTAINER GANTRY CRANES’ MACHINERY

Juan Jos´e Gonz´alez de la Rosa, J. M. Sierra, A. Illana, J. A. Carmona, L. M. Calvente

University of C´adiz, Electronics Area, Research Group PAIDI-TIC-168, EPSA

Av. Ram´on Puyol S/N, E-11202, Algeciras, C´adiz, Spain

Antonio Moreno Mu˜noz

University of C´ordoba, Electronics Area, Research Group PAIDI-TIC-168

Campus Rabanales, A. Einstein C-2. E-14071, C´ordoba, Spain

Keywords: Fault detection, Gantry crane, Higher-Order Statistics, Spectral kurtosis, Transient detection, Vibration moni-

toring.

Abstract:

The Spectral Kurtosis (SK) enhances non-Gaussian behavior associated to deviations from the nominal op-

eration of the cranes machinery. This fact easies fault detection, with the subsequent prevention of dramatic

malfunction. In this paper the rotor of a container gantry crane is monitored to get the kurtosis of its normal

operation. Then, two types of rolling bearings faults are modeled, according to the design of the rotors crane.

These signals are added to the real normal operation recordings, and processed under an estimator of the SK.

The experience allows the conformation of a higher-order statistical fault-pattern data base, without the need

of stopping huge machinery, and with the subsequent saving, settling the basis of an automatic surveillance

system.

1 INTRODUCTION

The study of the vibrations in a gantry crane used in

a containers’ terminal is an issue related to the secu-

rity of the crane operators and to the durability of the

design. Vibrations take place mostly in the operator’s

cabin and in the machinery hall; see the photo in Fig.

1 to get a ﬁrst approximation of the machinery under

test.

Numerous achievements have been made in the

ﬁeld of the control for overhead crane systems, which

have proven to be an improvement in the position ac-

curacy, safety and stabilization control. To cite: (Ju

et al., 2006; Hua and Shine, 2007; Lee et al., 2007).

Furthermore, in the work (De la Rosa et al., 2007, ),

the cabin system has been modeled with Simulink and

the vibration modes have been separated using the the

independent component analysis, settling the basis of

signal analysis in containers’ cranes systems.

In the ﬁeld of fault diagnosis, numerous improve-

ments have been made, cataloguing faults within big

machinery. The vast majority of the advances are

based in the traditional power spectral analysis, which

Figure 1: Container Gantry Cranes at Algeciras harbor.

is very sensible to noise and does not offer a com-

plete statistical characterization; in this sense, it is

very well known the potential usability of Higher-

Order Statistics (HOS) (De la Rosa and Mu˜noz, 2008,

). Among them, it is worthy remarkable the improve-

ment described in (Antoni, 2006) and (Antoni, 2007),

319

González de La Rosa J., Sierra J., Illana A., Carmona J., Calvente L. and Muñoz A. (2009).

AN APPLICATION OF THE SPECTRAL KURTOSIS TO MONITOR CONTAINER GANTRY CRANES’ MACHINERY.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 319-324

DOI: 10.5220/0002154703190324

 SciTePress

where the Spectral Kurtosis (SK) is applied to vi-

bratory surveillance and diagnostics of rotating ma-

chines; faults are modeled herein and characterized

using fourth-order statistics.

In this paper, the application of HOS consists of

characterizing the normal operation of a crane’s ro-

tor. Then, based in this nominal kurtosis, we add

two types of modeled faults to the normal operating

recordings. These faults are associated to different

catalogued defects in the rolling bearings (outer and

inner race defects), in order to obtain their character-

ization based in the SK. The rotor is located in the

machine hall of a container crane; so the described

fourth-order analysis of the pseudo-synthetic signals,

enables characterization without stopping the crane.

Faults are modeled according to the dimensions of the

rolling bearings.

An intermediate result proves the increment of the

non-Gaussian feature of the faults. From the global

calculation (numerical) of the kurtosis, we prove that

the nominal operation is slightly non-Gaussian, and

the kurtosis’ increment is associated to faulty bear-

ings. The main results will be concluded looking at

the frequency patterns of the faults recordings, and

they show the inter-frequency distance associated to

both fault types.

The paper is structured as follows. In Section 2

we make a brief summary on the deﬁnition of kurto-

sis; we use an unbiased estimator of the SK, success-

fully used in (De la Rosa and Mu˜noz, 2008, ), where a

higher measurement bandwidth was used. Fault mod-

eling is described in Section 3. Results are presented

in Section 4. Finally, conclusions are drawn in Sec-

tion 5.

2 KURTOSIS AND SPECTRAL

KURTOSIS

In statistics, kurtosis is a measure of the ”peakedness”

of the probability distribution of a random variable X.

Higher kurtosis means more of the variance is due to

infrequent extreme deviations, as opposed to frequent

modestly-sized deviations.

Kurtosis is more commonly deﬁned as the fourth

central cumulant divided by the square of the variance

of the probability distribution, which is the so-called

excess kurtosis, according to Eq. (1):

− 3, (1)

where µ

= κ

+ 3κ

is the 4th-order central mo-

ment; and κ

is the 4th-order central cumulant, i.d.

the ideal value of Cum

4,x

(0, 0, 0). This deﬁnition of

the 4th-order cumulant for zero time-lags comes from

a combinational relationship among the cumulants of

stochastic signals and their moments, and is given by

the Leonov-Shiryaevformula. A complete description

for these statistics can be found to cite in (Nikias and

Mendel, 1993; Mendel, 1991).

The ”minus 3” at the end of this formula is a cor-

rection to make the kurtosis of the normal distribution

equal to zero. Excess kurtosis can range from -2 to

+∞.

A high kurtosis distribution has a sharper ”peak”

and fatter ”tails”, while a low kurtosis distribution has

a more rounded peak with wider ”shoulders”. Distri-

butions with zero kurtosis are called mesokurtic (e.g

the normal distribution). A distribution with positive

kurtosis is called leptokurtic. A leptokurtic distribu-

tion has a more acute ”peak” around the mean and

”fat tails” (e.g. the Laplace distribution). A distribu-

tion with negative kurtosis is called platykurtic, which

has a smaller ”peak” around the mean and ”thin tails”

(e.g. the continuous or discrete uniform distributions,

and the raised cosine distribution; the most platykur-

tic distribution of all is the Bernoulli distribution).

In Measurement Science, the sample kurtosis is

calculated over a sample-register (an N-point data

record), and noted by:

− 3 =

i=1

− ¯x)

i=1

− ¯x)

− 3,

(2)

where m

is the fourth sample moment about the

mean, m

is the second sample moment about the

mean (that is, the sample variance), and ¯x is the sam-

ple mean. The sample kurtosis deﬁned in Eq. (2)

is a biased estimator of the population kurtosis, if we

consider a sub-set of samples from the population (the

observed data).

In the frequency domain, the ideal SK is a rep-

resentation of the kurtosis of each frequency compo-

nent of a process (or data from a measurement instru-

ment x

) (De la Rosa and Mu˜noz, 2008; Vrabie et al.,

2003, ). For estimation issues we will consider M re-

alizations of the process; each realization containing

N points; i.d. we consider M measurement sweeps,

each sweep with N points. The time spacing between

points is the sampling period, T

, of the data acquisi-

tion unit.

A biased estimator for the spectral kurtosis and for

a number M of N-point realizations at the frequency

index m, is given by Eq. (3):

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

320

N,M

2,X

(m) =

M − 1







(M + 1)

i=1

(m)|



i=1

(m)|



− 2







(3)

This estimator is the one we have implemented in

the program code in order to perform the data compu-

tation and it was also used successfully in (De la Rosa

and Mu˜noz, 2008, ). The estimator convergesin prob-

ability to the quantity being estimated (the true value,

) when the number of realizations M and the sam-

ple size N tend to +∞. So we say that the estimator is

asymptotically consistent with respect to M and N .

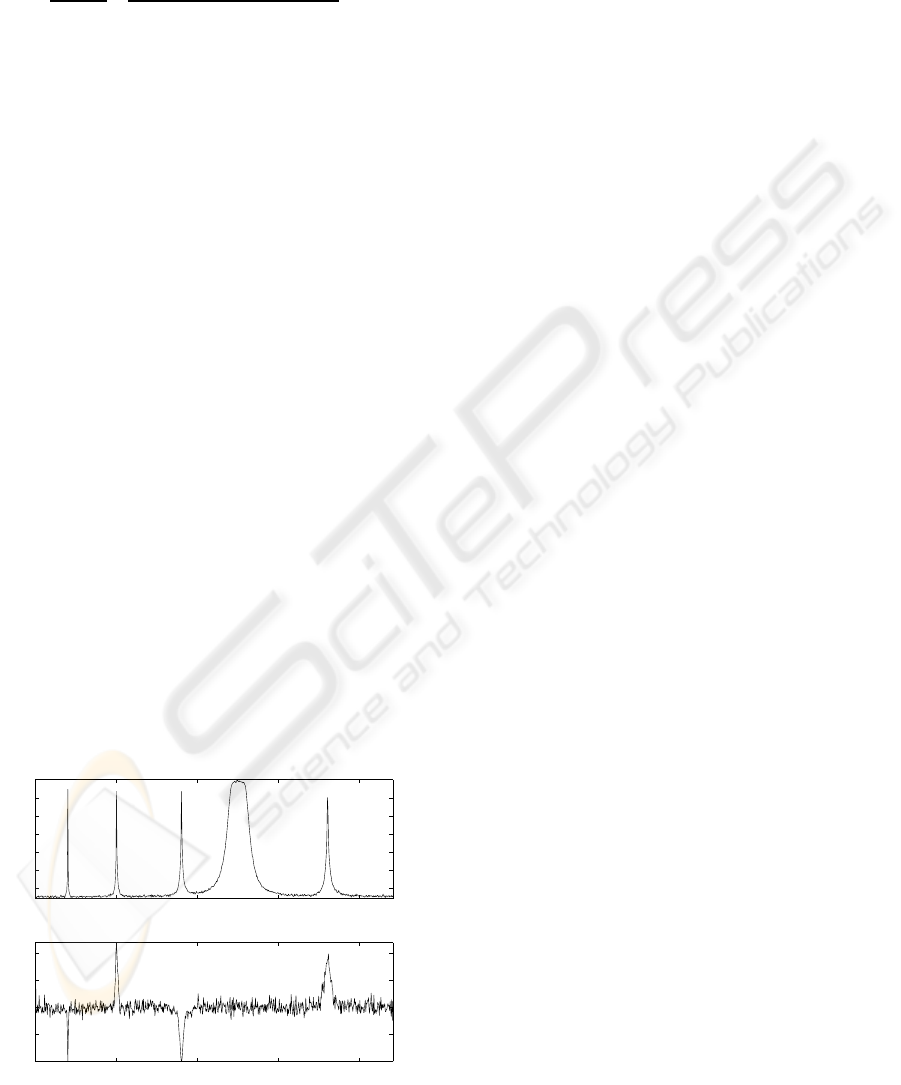
To show the ideal performance of the estimator,

which has been described in these lines, and also

described in (De la Rosa and Mu˜noz, 2008, ), we

show an example based in synthetics. A mix of

six different signals have been designed. Each mix-

ture is the sum of a constant-amplitude sine of 2

kHz, a constant-amplitude sine at 9 kHz, a Gaussian-

distributed-amplitude sine al 5 kHz, a Gaussian-

distributed-amplitude sine at 18 kHz, a Gaussian

white noise, and a colored Gaussian noise between

12 and 13 kHz. Each mixture (realization or sample

Negative kurtosis (”-1”) is expected for constant-

amplitude processes, positive kurtosis (not bounded

peaks) should be associated to random-amplitudes

and zero kurtosis will characterize both Gaussian-

noise processes. This is proved in Fig. 2, which

shows a good performance because enough registers

have been averaged (M=500).

The SK is supposed to behave similarly with syn-

0 5 10 15 20

−60

−50

−40

−30

−20

−10

Frequency, kHz

Normalised amplitude, dB

Averaged−normalised power spectrum

2 kHz

fixed ampl.

9 kHz

fixed ampl.

5 kHz

random ampl.

18 kHz

random ampl.

Colored

Gaussian

noise:

12−13 kHz

0 5 10 15 20

−0.5

0.5

Frequency, kHz

Kurtosis value

Averaged spectral kurtosis

2 kHz, kurtosis≈−1 9 kHz, kurtosis≈−1

5 kHz, kurtosis>0 18 kHz

kurtosis>0

Colored

Gaussian

noise: 12−13 kHz

kurtosis≈0

Figure 2: Performance over a set of synthetics, for M=500

realizations.

thetics associated to bearing fault modeling. As

we ﬁnd constant amplitude impulses (associated to

faults), an inﬁnite succession of ”-1” should appear in

the SK. This is also taken to measure inter-frequency

distances.

3 FAULT MODELING

Bearing components normally fail in the following or-

der: race defects (the most common), ball or roller

defects and cage defects (unless the bearing was de-

fective when installed). Inner race defects and fail-

ures occur at much lower amplitudes than outer race

defects.

BSF (Ball Spin Frequency) is usually generated

when a ball or roller is defective. When multiple balls

are defective, multiples of BSF appear, i.e., if BSF is

at 800 RPM and four balls have defects, you should

also see a peak at 3200 RPM or 4 × BSF. In all cases,

a surface defect on an inner race, an outer race or on

a roller (ball) generates shocks at the bearing charac-

teristic frequencies.

In a frequency spectrum, defects correspond to

pulse trains of frequencies extending from the 0-1000

Hz range in the domain of vibratory-acoustics. Such

families of peaks merge with the peaks due to other

causes. A real specialist must then deal with the bear-

ing analysis to sort out other causes present in the fre-

quency spectrum. In the vibration frequency range

(typically 10-1000 Hz), the patterns of frequency

spectra may indeed be complex, due to problems of

rotor dynamics; pumps ventilators (blade passing fre-

quencies, vanes, etc). This noise (usually Gaussian)

can be rejected using HOS.

In the present work, we have modeled the outer

race and the inner race faults, which are the most

usual. Both faults are modeled with the same im-

pulses’ amplitudes. The following modeled magni-

tudes are exposed according to the jargon’s nomen-

clature. The rotation speed (RPM/60), f = 1 Hz;

BPFI (Bearing Inner Race Frequency) = 13 Hz; BPFO

(Bearing Outer Race Frequency) = 7 Hz; BSF (Ball

Spin Frequency)

∼

1.15 Hz; FTF (Fundamental Train

Frequency)

∼

0.35 Hz.

The above magnitudes have been calculated

considering the dimensions of the rolling bearing:

contact angle (α) = zero; B

(ball or roller diameter)

= 65 mm; P

(pitch diameter) = 215 mm; N

(number

of balls, or rollers) = 20. The following expressions

expanded in Eq. (4), allow calculation for the present

situation:

AN APPLICATION OF THE SPECTRAL KURTOSIS TO MONITOR CONTAINER GANTRY CRANES'

MACHINERY

321

BP F O = f ×



1 −

P d

× cos(α)



BP F I = f ×



1 +

P d

× cos(α)



BSF = (f/2) ×



1 −

P d

× cos

(α)



F T F = (f/2) ×



1 −

P d

× cos(α)



(4)

According to Eq. (4), outer and inner faults have

been modeled with the form of impulse trains whose

pulse repetition rate obeys the calculation performed

in Eq (4). Two sample registers are depicted in Fig. 3.

0 1 2 3 4 5 6 7 8 9 10

−4

−2

Time, sec.

Acceleration, m/s

Outer−fault data, kurtosis=8.513

0 1 2 3 4 5 6 7 8 9 10

−6

−4

−2

Time, sec.

Acceleration, m/s

Inner−fault data, kurtosis=6.316

Figure 3: Two data registers which model both types of

faults in the rotor’s rolling bearings. Impulse repetition:

BPFI (Bearing Inner Race Frequency) = 13 Hz; BPFO

(Bearing Outer Race Frequency) = 7 Hz.

It is also seen in Fig. 3, the background raw data,

which corresponds to normal operation. A SNR of 6

dB has been ﬁxed (variance of the normal vibration,

4; variance of the pulse trains 8). According to this

model, results for the SK analysis are presented here-

inafter.

4 EXPERIMENTS AND RESULTS

We show the experimental location of the sensors in

Fig. 4. Three sensors are primarily connected to the

rotor carcase, aiming to conﬁrm the similarity of the

three signals, in order to reduce the three to one mea-

surement point. The rotor’s structure under test is lo-

cated inside the machine room of the crane (see Fig.

1).

Industrial accelerometers (model KD42V) have

been used with a sensitivity of 100 mV/g, which is

the usual standard in noise and vibration control En-

gineering. The sensors’ usable bandwidth is of 100

kHz. Despite the fact that low-frequency vibrations

are involved, the sampling frequency was set to 10

kHz in order to capture high resolution recordings,

aiming to buried them with modeled impulses’ trains.

Figure 4: A photograph of the rotor and the location of the

sensors.

The kurtosis as a global indicator, considered as

the average of the kurtosis computed for each individ-

ual frequency component, is not a valid tool to extract

features. This is due to the fact that no discrimination

is made neither among the frequency bands nor the

frequency pattern, from the global point of view.

In order to get a reliable characterization, each

(102,714; about 10 sec. sampling). In normal oper-

ation, the mean value of the excess kurtosis is 1.343,

which is somewhat over the Gaussian limit (kurtosis

= 0). For the outer fault case, the median of the kur-

tosis is 8.513. The inner fault is characterized by an

average kurtosis of 6.316. This by the way is an indi-

cation of the type of fault. But the global indication is

very susceptible to errors associated to transients, or

other non-Gaussian noise, and does not provide infor-

mation relative to the frequency bands.

So, the key of the SK detection strategy used in

this work, lies in the potential enhancement of the

non-Gaussian behavior of the vibrations. If this hap-

pens, i.e. if an increase of the non-Gaussian activ-

ity (increase in the kurtosis, peakedness of the prob-

ability distribution) is observed-measured in the SK

graph, there may be deviation from normal function-

ing.

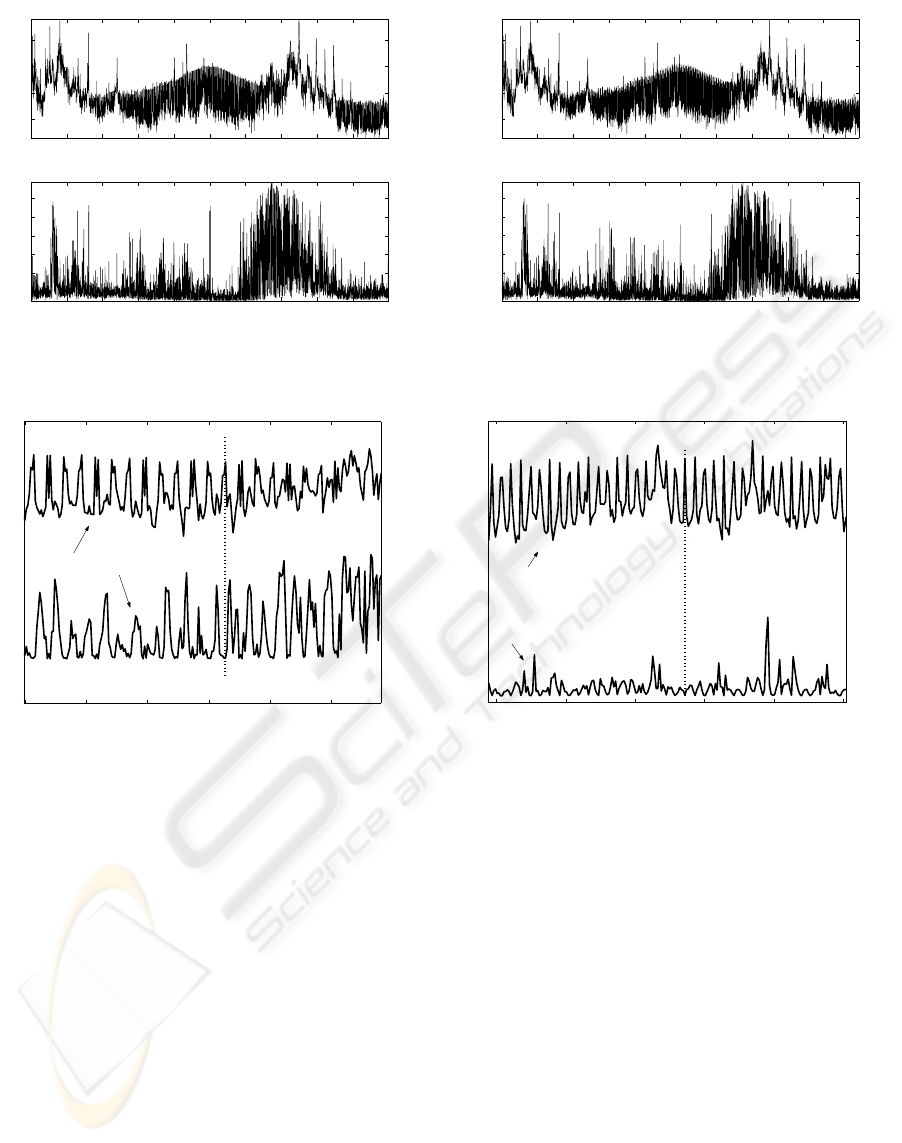
Fig. 5 shows the frequency analysis associated to

one recording, which models an inner race defect in

the rotor bearing. At a ﬁrst glance, it is difﬁcult to

reach a frequency pattern, but a closer examination

reveals the constant inter-frequency distance which

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

322

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

−40

−20

Frequency, Hz

Amplitude, dB

Inner race fault case

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

Frequency, Hz

Kurtosis value

Figure 5: High resolution frequency analysis of an inner

race fault.

2950 3000 3050 3100 3150 3200

Frequency, Hz

Inner race fault case

Spectrum

Spectral Kurtosis

Peak correspondence

Figure 6: High resolution frequency analysis of an inner

race fault. A zoom of Fig. 5. Graphs have been shifted for

convenience. Inter-frequency = 13 Hz.

characterizes this type of fault.

Fig. 7 presents the spectral analysis of an outer

race fault, which is very similar to the inner fault case,

depicted in Fig. 6.

On the basis of the second and fourth-order spec-

tra, we conclude the possibilities of the SK to distin-

guish between two common faults in rotor bearings.

5 CONCLUSIONS AND

ACCOMPLISHMENTS

Results show the potential use of the SK to target

faults in mechanical systems. Concretely, the estima-

tor of the SK is able to discriminate between two dif-

ferent faults, commonly encountered in rolling bear-

ings, and targeted here via the inter-frequency dis-

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

−40

−20

Frequency, Hz

Amplitude, dB

Outer race fault case

0 500 1000 1500 2000 2500 3000 3500 4000 4500 5000

Frequency, Hz

Kurtosis value

Figure 7: High resolution frequency analysis of a fault in

the outer race.

2300 2350 2400 2450 2500 2550

Frequency, Hz

Outer race fault case (zoom)

Spectrum

Spectral kurtosis

Peak correspondence

Figure 8: High resolution frequency analysis of an outer

race fault. A zoom of Fig. 7. Graphs have been shifted to

improve visualization. Inter-frequency = 7 Hz.

tance.

The improved performance of the SK over the

global excess kurtosis resides in the possibility of an-

alyzing separated frequency bands, or inter-frequency

distances, which are more indicative features of faults

than a mere numeric statistical calculation. The kur-

tosis as a global indicator is considered only a prior

indication of the fault.

The interest of the experiment resides in the possi-

bility of incorporate this signal processing algorithm

to the engine of an expert system in order to monitor

on-site performance of machinery, and get a predic-

tive surveillance. This would be done without stop-

ping production of such big machinery.

AN APPLICATION OF THE SPECTRAL KURTOSIS TO MONITOR CONTAINER GANTRY CRANES'

MACHINERY

323

REFERENCES

Antoni, J. (2006). The spectral kurtosis: application to the

vibratory surveillance and diagnostics of rotating ma-

chines. Mechanical Systems and Signal Processing

(Ed. Elsevier), 20(2):308–331.

Antoni, J. (2007). Cyclic spectral analysis in practice. Me-

chanical Systems and Signal Processing (Ed. Else-

vier), 21(2):597–630.

Hua, Y. J. and Shine, Y. K. (2007). Adaptive coupling con-

trol for overhead crane systems. Mechatronics, (-):in

Press.

Ju, F., Choo, Y., , and Cui, F. (2006). Dynamic response of

tower crane induced by the pendulum motion of the

payload. International Journal of Solids and Struc-

tures, (43):376–389.

Lee, D.-H., Cao, Z., and Meng, Q. (2007). Scheduling of

two-transtainer systems for loading outbound contain-

ers in port container terminals with simulated anneal-

ing algorithm. Int. J. Production Economics, (-):in

Press.

Mendel, J. M. (1991). Tutorial on higher-order statistics

(spectra) in signal processing and system theory: The-

oretical results and some applications. Proceedings of

the IEEE, 79(3):278–305.

Nikias, C. L. and Mendel, J. M. (1993). Signal process-

ing with higher-order spectra. IEEE Signal Processing

Magazine, pages 10–37.

De la Rosa, J. J. G. and Mu˜noz, A. M. (2008). Higher-order

cumulants and spectral kurtosis for early detection of

subterranean termites. Mechanical Systems and Sig-

nal Processing (Ed. Elsevier), 22(Issue 1):279–294.

Available online 1 September 2007.

De la Rosa, J. J. G., Puntonet, C. G., Moreno, A., Il-

lana, A., and Carmona, J. A. (2007). An application

of ICA to BSS in a container gantry crane cabin’s

model. Lecture Notes in Computer Science (LNCS),

4666:714–721. 7th International Conference on Inde-

pendent Component Analysis and Signal Separation

(ICA 2007) London, UK, September 9-12, 2007, Pro-

ceedings.

Vrabie, V., Granjon, P., and Serviere, C. (2003). Spectral

kurtosis: from deﬁnition to application. In IEEE, edi-

tor, IEEE-EURASIP International Workshop on Non-

linear Signal and Image Processing (NSIP’2003), vol-

ume 1, pages 1–5.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

324