INTELLIGENT FAULT DIAGNOSIS

USING SENSOR NETWORK

Haris M. Khalid, Rajamani Doraiswami

Systems Engg. Department,King Fahd University of Petroleum and Minerals, Dhahran 31261, Kingdom of Saudi Arabia

Department of Electrical and Computer Engineering, University of New Brunswick, Fredericton, New Brunswick, Canada

Lahouari Cheded

Systems Engg. Department, King Fahd University of Petroleum and Minerals, Dhahran 31261, Kingdom of Saudi Arabia

Keywords: Incipient faults, Holistic approach, Fault diagnosis, Model based, Integrated approach.

Abstract: An intelligent diagnostic scheme using sensor network for incipient faults is proposed using a holistic

approach which integrates model-, fuzzy logic-, neural network- based schemes. In case the system is highly

non-linear and there are enough training data available, a neural network based scheme is preferred; where

the rules relating the input and output can be derived, a Fuzzy-logic approach is chosen; and where a model

is available, a linearized model is employed. These three schemes are integrated sequentially ensuring

thereby that critical information about the presence or absence of a fault is monitored in the shortest possible

time, and the complete status regarding the fault is unfolded in time. The proposed scheme is evaluated

extensively on simulated examples and on a physical system exemplified by a benchmarked laboratory-

scale two-tank system to detect and isolate faults including sensor, actuator and leakage ones.

1 INTRODUCTION

Fault

is an undesirable factor in any process control

industry. It affects

the efficiency of system operation

and reduces economic benefit to the

industry. The

early detection and diagnosis of faults in mission

critical systems becomes highly crucial for

preventing failure of equipment, loss of productivity

and profits, management of assets, reduction of

shutdowns, condition-based monitoring, product

quality, process reliability, economy, potential

hazards, pollution, and conservation of scarce

resources. In a chemical industry, the release of

hazardous chemicals into the environment requires

quick action to limit the harmful impact of such a

release. Of much concern is the purposeful release of

chemicals in order to cause harm. Quickly detecting

and identifying an unknown threat caused by a fault

is pivotal to limiting harm and possibly saving lives.

Because of the large area covered in either a process

control industry or water distribution systems, a

single technique is not able to monitor all of the

activity in the area of concern. For this reason, a

precise pool of intelligent approaches is being

developed to create a better response plan. There

must be a way to process and clearly present an

accurate picture of the fault threat. Information

about the constraints associated with an early

detection of hazardous material in the environment

help shape the proposed methodology, and is one of

the main motivations for embedding intelligent tools

in diagnosis and decision making (

R.J. Patton, 2000).

The purpose of this paper is to present and

advance a new methodology for the intelligent

detection of incipient faults. New methods of

assimilating information from highly complex and

nonlinear physical systems with various

nonlinearities are being developed. Intelligent tools

that have the ability to adapt, such as neural

networks and fuzzy inference systems, are brought

to bear on both of these aims. Data from a

benchmarked laboratory-scale two-tank system is

used and the proposed approach evaluated.

The faults include sensor, actuator and leakage

faults, and they can be classified broadly as either

parametric faults or additive ones. An additive fault

manifests itself as an additive exogenous signal in

the measured data, while a parametric fault induces a

121

M. Khalid H., Doraiswami R. and Cheded L.

INTELLIGENT FAULT DIAGNOSIS USING SENSOR NETWORK.

DOI: 10.5220/0002165201210128

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page

ISBN: 978-989-8111-99-9

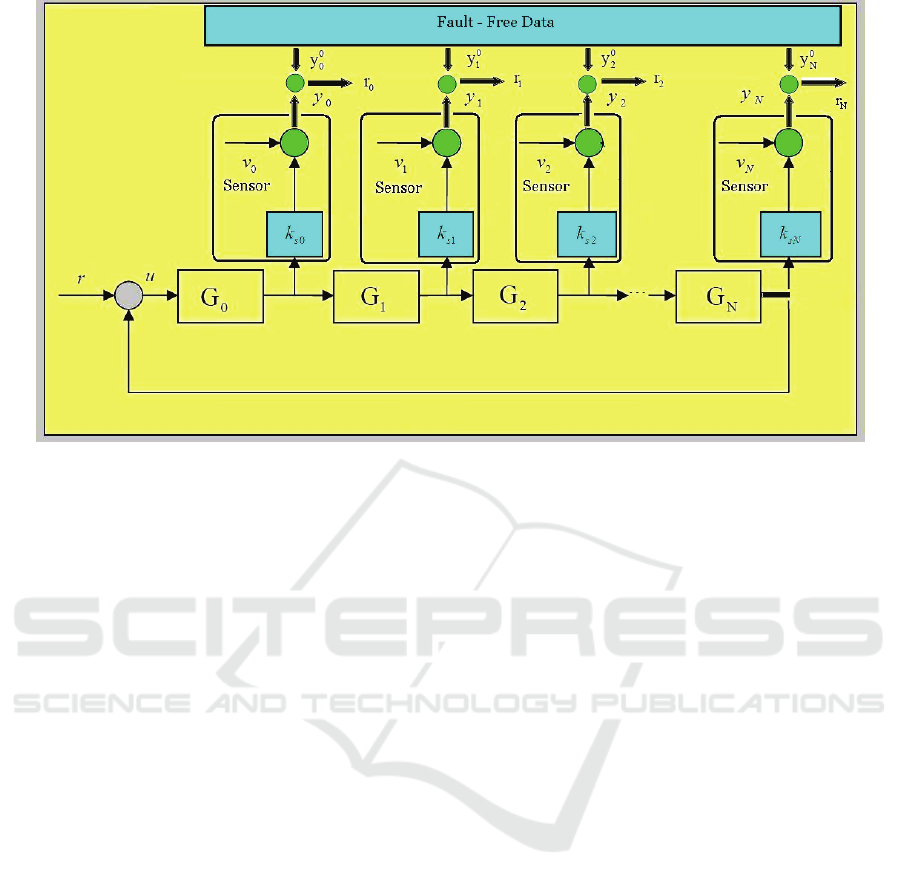
Figure 1: Sensor Network.

variation in the system parameters.

The fault diagnosis scheme can be carried out

using a neural network, or fuzzy logic or a model-

based technique

(L. B. Palma, 2003). While neutral

networks can be used to quickly and correctly

classify a particular fault, they cannot unravel it and

point out its root causes. However, these root causes

can be uncovered by supplementing the neural

network used by a fuzzy logic scheme, which

through the very makeup of its rules, will accurately

, albeit more slowly than the neural network,

pinpoint the cause(s) that spawned this fault. The

synergistic value of this integration will no doubt

provide a powerful fault detection scheme. The

neural net and fuzzy logic approaches are not geared

for the diagnosis of incipient faults, hence the need

for, and the inclusion of, a model-based scheme.

2 A SENSOR NETWORK

PARADIGM FOR FAULT

DIAGNOSIS

A new scheme is proposed here whereby a sensor

network paradigm is applied to fault diagnosis. A

typical system including a process control system, a

water distribution system formed of tanks and

network of pipes, a power utility formed of

generators and transmission lines, a communication

network, and petrochemical industries consisting of

a number of control loops, including controllers,

sensors and actuators, and various processing plants,

as shown in Fig. 1. As such, such a large system will

include a sensor network.

A sensor is modelled by a gain and an additive

noise, as given below:

isiii

ykyv

(1)

where

y ,

and

v are the measured sensor

output, true or fault-free output and additive noise,

respectively. Here the gain is such that

k≤≤,

with the degree of the fault ranging from no fault at

all for

to a complete failure for 0

k = . The

subsystems such as actuators, processors and

controllers are denoted by transfer functions,

G .

Many systems consisting of several closed loops,

each with its own reference input, can be viewed as

a sensor network that can be described by a ring-

type topology.

The objective of the sensor network is to

diagnose faults in both the sensors, through the gains

k and in the subsystems

G by monitoring the

sensor outputs

y .

The mathematical relations governing the sensor

outputs

y to the input to

G , denoted by e are:

1000s

yGkev

20111s

yGGkev

301222s

yGGGkev

012 1 (1) 1

...

iisii

yGGGGk ev

−

−−

(2)

where ery

− .

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

122

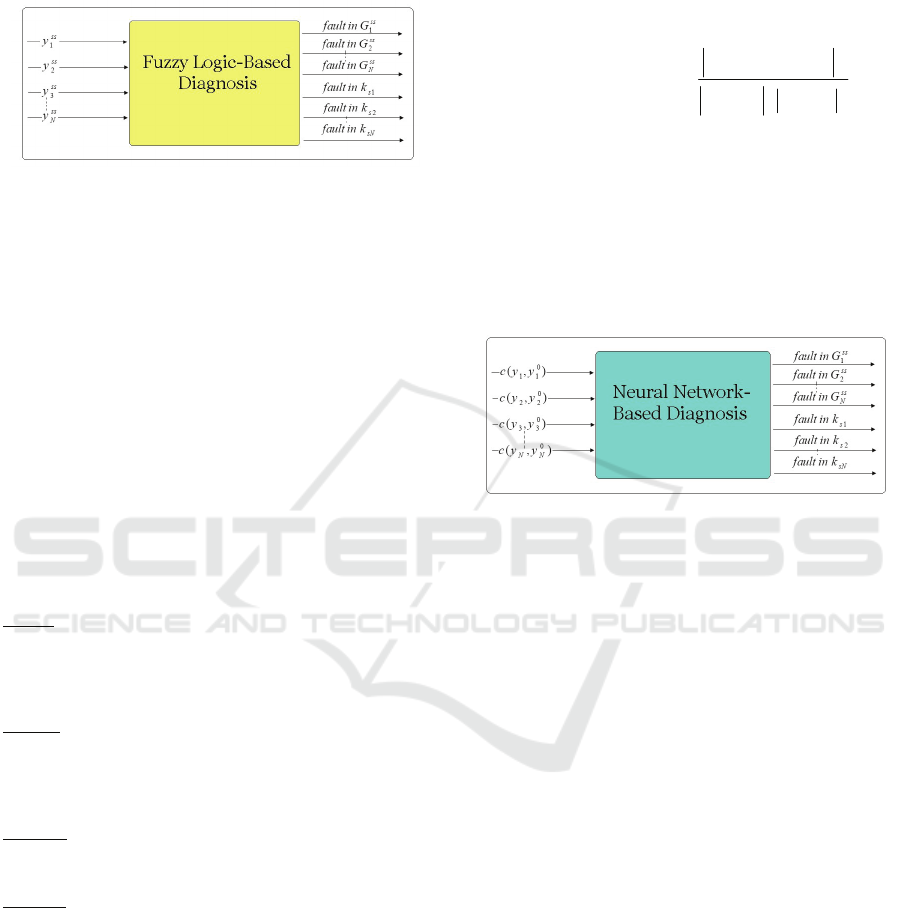
3 FUZZY LOGIC-BASED FAULT

DIAGNOSIS

Figure 2: Fuzzy Logic-Based Fault Diagnosis Scheme.

The fuzzy fault diagnosis scheme uses the steady-

state values of the sensor outputs,

y , denoted by

A change in the gain

k or a change in the steady-

state gain of the transfer function

G , denoted

, is indicative of a fault in the i-th sensor and

i-th subsystem, respectively (see Fig.2). Assuming

that the noise term is subsumed in the fuzzy

membership function, the steady-state model takes

the form:

01 2 1(1)

...

ss ss ss ss ss

iisi

GGG G k e

−−

(3)

Let us now define linguistic variables such as

zero, and non-zero. For simplicity, we will consider

the case where only one device can be faulty at any

given time, i.e. the fault is assumed to be simple. In

this case, the fuzzy rules may take the following

form:

Rule 1

: If

is non-zero, then there is a fault in the

steady-state gain

G or

G or…or

G or ith

sensor gain

Rule II

: If

is zero, then there is no fault in the

subsystem’s steady-state gain

G or

G or…or

G or ith sensor gain

Rule III

: If

is zero and

(1)si

is non-zero then

there is a fault in subsystem

or sensor

(1)si

Rule IV

: If

is non-zero and

(1)si

is zero then

there is a fault in sensor

These rules may be generalized to multiple faults.

4 NEURAL NETWORK-BASED

FAULT DIAGNOSIS

A fault in the sensor,

k , and or in a subsystem,

G , can also be diagnosed by using a neural

network, as shown in Fig.3. The inputs to the neural

network are the spectrum of the coherence between

the fault-free and measured sensor outputs.

(4)

where

is the frequency in rad/sec, and

(

)

(

)

()

cy j y j

is the coherence spectrum. If

there is no fault, then

()

(

)

() 1

cy j y j

ωω

= for all

frequencies. If the measured and fault-free outputs

are incoherent with each other at some frequencies,

then the coherence spectrum will be less than 1 at

those frequencies.

Figure 3: Neural Network-Based Fault Diagnosis Scheme.

5 MODEL-BASED FAULT

DIAGNOSIS

A bank of Kalman filters is employed to detect

faults. An i-th Kalman filter will be driven by the

signal

()ek , and the output of the i-th sensor output

y ,

(

)

(1) () ( ) () ()

iiii iii

kAxkBekdKykyk+= + − + −

ˆˆ

() ()

iii

yk Cxk

(5)

where

d is the delay,

is the estimate of the state,

(

)

iii

BC is the state-space model of the

system with input

()ek and the sensor output, ()

yk.

The above-defined Kalman filter is applied to the

following transfer function model of the collection

of i sub-systems:

012 1 (1) 1

...

iisii

yGGGGk ev

−

−−

(6)

5.1 Kalman Filter Design

Let us consider a generic Kalman filter for a system

with input u and output, y. The Kalman filter is

()

()()

,( )

() ()

yj yj

cy j y j

yj yj

ωω

INTELLIGENT FAULT DIAGNOSIS USING SENSOR NETWORK

123

designed for the normal fault-free operation. The

model of the fault-free system is given by:

(1) () ( ) ()xk Axk Buk d wk+= + −+

() () ()yk Cxk kυ=+

(7)

Where

()

000

,,ABC are the system matrices

obtained from the fault-free system model,

()wk and

()vk are the zero-mean white plant and

measurement noise signals, respectively, with

covariances:

() ()

QEwkwk

⎡⎤

⎣⎦

, and () ()

REvkvk

⎡⎤

⎣⎦

(8)

The plant noise,

()wk , is a mathematical artifice

introduced to account for the uncertainty in the

priori

knowledge of the plant model. The larger the

covariance

Q is, the less accurate the model

()

000

,,ABC is and vice versa.

The Kalman filter is given by:

(

)

00 0 0

ˆˆ ˆ

(1) () ( ) () ()xk Axk Buk d K yk Cxk+= + −+ −

() () ()

ek yk Cxk=−

(9)

where

d is the delay and ()ek the residual.

The system model has a pure time delay which is

incorporated in the Kalman filter formulation. The

Kalman filter estimates the states by fusing the

information provided by the measurement

()yk

and the

a-priori information contained in the

model,

()

000

,,ABC . This fusion is based on the a

priori

information of the plant and the measurement

noise covariances, Q, and R, respectively. When Q is

small, implying that the model is accurate, the state

estimate is obtained by weighting the plant model

more than the measurement one. The Kalman gain,

K , will then be small. On the other hand, when R

is small implying that the measurement model is

accurate, the state estimate is then obtained by

weighting the measurement model more than the

plant one. The Kalman gain,

K , will then be large

in this case.

The larger

K is, the faster the response of the

filter will be and the larger the variance of the

estimation error becomes. Thus, there is a trade-off

between a fast filter response and a small covariance

of the residual. An adaptive on-line scheme is

employed to tweak the

a- priori choice of the

covariance matrices so that an acceptable trade-off

between the Kalman filter performance and the

covariance of the residual is reached.

5.2 Fault Isolation

Let

e be the residual of the i-th Kalman filter. A

fault in

G ,

G …or

G or

k is indicated if the

absolute mean of the residual exceeds a specified

threshold

σ .

Let us define a 2(N+1) by1 vector of zeros and ones.

012 012

... ...

iN N

bggg g

κκκ κ

⎡⎤

⎣

⎦

(10)

no fault in G

ault in G

⎧

⎨

⎩

(11)

no fault in k

ault in k

⎧

⎨

⎩

(12)

Case I.

If the absolute mean of the i-th residual exceeds the

threshold

σ , then

b will be:

1 1 1 .... 1 ...

b X XX XX XXX

⎡⎤

⎣

⎦

(13)

where X is a don’t care value (0 or 1).

If the absolute mean of the (i+1)-st residual does

not exceed the threshold

σ , then

will be:

0000 .... 0 ...

bXXXXXXX

⎡⎤

⎣

⎦

(14)

The intersection between the 2 binary sets

b and

, amounting to an element-wise binary logical

ANDing of these 2 sets, will then clearly indicate

that the sensor

k is the faulty one.

Case II.

If the absolute mean of the ith residual does not

exceed the specified threshold

σ , then

b will be:

0 0 0 .... 0 ...

bXXXXXXXX

⎡⎤

⎣

⎦

(15)

If the absolute mean of the (i+1)-st residual

exceeds the specified threshold

σ , then

will

be:

1 1 1 1 .... 1 ...

bXXXXXXX

⎡

⎤

⎣

⎦

(16)

This shows that the intersection between the 2

binary sets

b and

, amounting to an element-

wise binary logical ANDing of these 2 sets, will

then clearly indicate that either the sensor

(1)si

subsystem

(1)si

is the faulty one.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

124

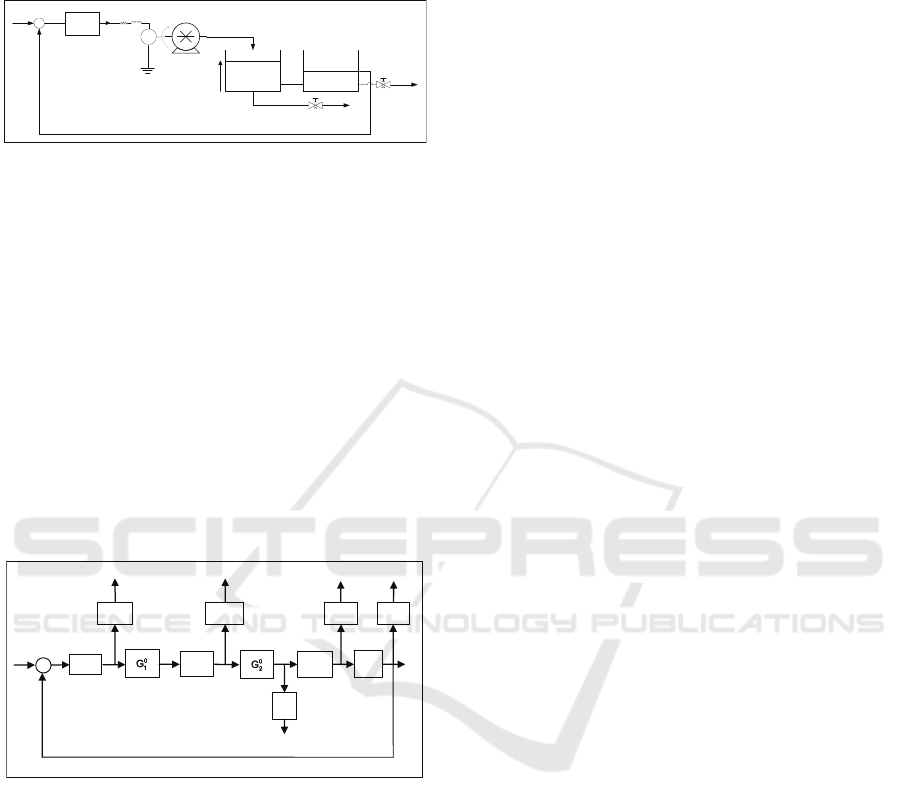
6 EVALUATION OF THE

PROPOSED SCHEME

pump

dc motor

leakage

controller

outflow

inflow

Figure 4: Two-tank Fluid System.

An evaluation of the proposed scheme for fault

diagnosis was performed on a benchmark

laboratory-scale process control system using

National Instruments LABVIEW as shown in Fig 4.

Fault diagnosis in a fluid system has enjoyed an

increasing importance and popularity in recent years

from the points of view of economy, safety,

pollution, and conservation of scarce resources

(Marco Ferrente, 2008) (Zhang Sheng,

2004)(Doraiswami, 1996) (R.J. Patton,

2000)(Astrom et.,al, 2001) (C. De Persis, 2000)(

Hammouri

, 2002) (K.M. Kinnaert, 1999).

The proposed scheme is used to detect and isolate

a fault by a sequential integration of model-free and

model-based approaches.

leakage

tank

actuator

controller

1-γ

Figure 5: Fluid system subject to a leakage.

We will use a set of fuzzy logic rules to detect a

leakage. The fuzzy IF and THEN rules for the two-

tank fluid system are derived using the sensor

network shown in Fig.1. For the fault diagnosis

problem, the equivalent of Fig. 1, is shown in Fig. 5

whose various sub-systems and sensor blocks are all

explained below. First, note that the first two blocks

in Fig. 5, i.e.

G and

= , represent the

controller and the actuator sub-systems, respectively.

As shown in Fig. 5, the leakage is modelled by the

gain

which is used to quantify the amount of

flow lost from the tank. Thus the net outflow is

quantified by the gain (

−

). Since the two blocks

G and (1

−

) cannot be dissociated from each

other, they are fused into a single block labelled

(

)

1GG

=−

. The feedback sensor, modelled by

the gain

k , is used to feed the plant output y back to

the controller, and is modelled by the last block

in Fig. 3, where

. An additional sensor,

termed as the redundant sensor of gain

k , is used

here to discriminate between faults in the height

sensor and feedback sensor. Even though the

control input

u does not necessitate a separate sensor

to monitor its output as it is freely available from the

digital controller (

G ), a separate unit gain, labelled

, is attributed to it. Similarly, the last sensor,

used to monitor the feedback sensor output, is also

attributed a unit gain, i.e.

k = . The reason for

adding these two unit gains to Fig. 5 is motivated by

our desire to make the overall sensor network

structure for the leakage detection problem fit in

well within the general sensor network-based fault

detection paradigm shown in Fig. 3. By doing so, the

two fuzzy rules (Rules 1 and 2 given earlier) can be

readily applied to Fig. 5. The four residuals,

r ,

r and

r , are the deviations between the fault-free

and fault-bearing measurements of the control input

, flow rate, height from the redundant sensor, and

height from the feedback sensor, respectively.

6.1 Fault Diagnosis using a Model-free

Approach

A sequential integration of an artificial neural

network (ANN) and a fuzzy logic (FL) approach is

employed here to isolate faults.

Fuzzy-logic Approach. The features were chosen

to be the steady-state values of the control input,

u ,

measured flow

lw and height

h values and their

fault-free counterparts,

u ,

lw and

h , respecti-

vely. The fuzzy logic rules pertinent to this case are

similar to those described earlier.

The steady-state gain relating

lw and

u is

given by:

sssss

lw G G u=

(17)

The steady-state gain relating

h and

u is

given by:

01 2

sssssss

h GGGu=

(18)

INTELLIGENT FAULT DIAGNOSIS USING SENSOR NETWORK

125

Where

01 2

sssss

GGG

are the steady-state gains of

the actuator, the transfer function relating the control

input to the flow, and the transfer function relating

the flow to the height, respectively.

The fuzzy IF

-and-THEN rules given in the

previous section can isolate a leakage from faults in

the actuator, flow and height (or level) sensor.

Neural Network Approach. A neural network is

driven by the coherence spectrum between the

measured height

h and the corresponding fault-free

one

h . This coherence spectrum is defined by:

(19)

The neural network is trained to classify four

possible faults, namely a fault in the actuator, a fault

in the level sensor, a fault in the flow sensor, and a

leakage.

The fuzzy approach is then integrated

sequentially with the neural network-based fault

classification approach to complete the required

fault isolation scheme. The Neural Network-based

classifier precedes the Fuzzy Logic-based one, with

the former providing a fast fault classification,

followed by a fuzzy logic block to unravel the real

cause(s) of the fault. The fault magnitude is

estimated from the changes in the settling time,

ss ss

tttΔ= − , whereas its onset is indicated by the

changes in the height profile.

Figs 6-8 give the profiles of the flow, height and

the coherence spectrum. Fig. 6 shows height profiles

in the presence of leakages of different magnitudes

occurring when the fluid level system is operated in

both an open-loop and a closed-loop configuration.

For the open-loop case, one can readily deduce both

the onset and amount of the leakage from the

height/flow profile. The leakage flow has five

sections corresponding to the following five degrees

of no-leakage, small, medium, large and very large

leakage. However, by its very nature, the closed-

loop PI controller hides the fault and hence makes it

difficult to visually detect it.

0 200 400 600 800 1000 1200 1400 1 600 1800 2000

100

150

200

250

300

time t

Hydraulic Height

Height /Flow Profiles for PI Controll er with Consumer

no leakage

small

medium

large

very large

0 200 400 600 800 1000 1200 1400 1 600 1800 2000

time t

Hydrauli c Fl ow

no leakage

small

medium

large

very large

0 0. 1 0.2 0. 3 0.4 0.5 0.6 0. 7 0. 8 0.9 1

0.82

0.84

0.86

0.88

0.9

0.92

0.94

0.96

0.98

frequency

coherenc e

coherenc e spec trum of leak age faults

large

medium

small

Figure 6: Height/Flow Profile/Coherence under leakage

Faults.

0 200 400 600 800 1000 1200 1400 1600 1800 2000

100

200

300

time t

Hydraulic Height

Height/ Flow Profiles for PI Controller wi th Cons umer

act uator fault=0. 25

act uator fault=0. 50

act uator fault=0. 75

act uator fault=1. 0

0 200 400 600 800 1000 1200 1400 1600 1800 2000

time t

Hydraulic Flow

act uator fault=0. 25

act uator fault=0. 50

act uator fault=0. 75

act uator fault=1. 0

0 0. 1 0.2 0. 3 0. 4 0. 5 0.6 0.7 0.8 0.9 1

0.65

0.7

0.75

0.8

0.85

0.9

0.95

frequency

coherenc e

coherenc e spec trum of ac tuato r faults

large

medium

small

smaller

Figure 7: Height/FlowProfile/Coherence under actuator

faults.

0 500 1000 1500 2000 2500 3000 3500 4000 4500

100

200

300

time t

Hydrauli c Height

Height /F low for PI Cont roller with Con sum er

sensor fault=0.25

sensor fault=0.50

sensor fault=0.75

sens or fault=1.0

0 500 1000 1500 2000 2500 3000 3500 4000 4500

time t

Hydraulic Flow

sens or fault=0.25

sens or fault=0.50

sens or fault=0.75

sens or fault=1.0

0 0. 1 0.2 0. 3 0. 4 0. 5 0.6 0.7 0.8 0.9 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

frequency

coherenc e

coherenc e spec trum of s ensor fault s

large

medium

small

smaller

Figure 8: Height/Flow Profile/Coherence under level

sensor faults.

6.2 Model of the Fluid System

A benchmark model of a cascade connection of a dc

motor and a pump relating the input to the motor,

and the flow,

Q , is a first-order system expressed

by:

()

imim

QaQbu

=− +



(20)

where

a and

b are the parameters of the motor-

pump system and

()u

is a dead-band and

saturation-type nonlinearity. The Proportional and

Integral (PI) controller is given by:

3pI

erh

ukekx

=−



(21)

where

k and

k are gains and r is the reference

input.

With the inclusion of the leakage, the liquid level

system is modelled by (Astrom et al., 2001):

()()

112121i

QC H H C H

ϕϕ

=− − −

(22)

()()

2121202

CHHCH

ϕϕ

=−−

(23)

where

(.) (.) 2 (.)

ign g

= ,

()

QC H

is the

leakage flow rate,

()

00 2

QC H

= is the output flow

rate,

and

are the liquid heights in tanks 1 and

2, respectively,

and

are the cross-sectional

areas of tanks 1 and 2, respectively, g=980

/seccm

is the gravitational constant,

C and

C are the

()

,( )

()

hjhj

ch j hj

hj hj

ωω

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

126

discharge coefficients of the inter-tank and output

valves, respectively. The linearized model of the

entire system formed of the motor, pump, and the

tanks is given by:

Ax Br y Cx=+ =



(24)

11 1

1000

001 , [1000]

mp mI m

aa b

bk bk a

BbkC

−−

⎡⎤

⎢⎥

−−

⎢⎥

−

⎢⎥

−−

⎢⎥

⎣⎦

⎡⎤

⎣⎦

(25)

Where

q , q

q ,

h and

h are respectively the

increments in

Q , Q

Q ,

and

a ,

and

are parameters associated with linearization,

is associated with leakage and

is the output

flow rate,

= .

6.3 Evaluation of the Fault Detection

using a Bank of Kalman Filters

A bank of two Kalman filters is used here, one with

input u(k) and the flow-sensor output, and the other

with input u(k) and the height-sensor output

First the fault-free model of the system is

identified using a recursive least-squares

identification scheme. The order of the estimated

model was iterated to obtain an acceptable model

structure using a combination of the AIC criterion

and the identified pole locations.

The identified model is essentially a second-order

system with a delay even though the theoretical

model is of a fourth order. Using the fault-free

model together with the covariance of the

measurement noise, R, and the plant noise

covariance, Q, the Kalman filter model was finally

derived. As it is difficult to obtain an estimate of the

plant covariance, Q, a number of experiments were

performed under different plant scenarios to tune the

Kalman gain,

K .

()

ˆˆ ˆ

(1) () ( ) () ()

iiiii iiii

xk Axk Buk d Kyk Cxk+= + −+ −

(26)

() () () 1,2

iii

rk yk Cx k i=− = (27)

where

is the state,

r is the residual, (,, )

iii

BC is

the state-space model of the first subsystem relating

the control input

()uk to the flow output ()

yk. The

transfer function for the first subsystem

111

(,, )

BC relating the control input ()uk to the

flow output

()yk.

101

() () ()()yz GzGzuz

(28)

where

G is the actuator transfer function and

G is

the transfer function relating the actuator output to

the flow.

222

(, , )

BC is the state-space model for

the second subsystem relating the control input

()uk

to the height

()yk. The transfer function for the

second subsystem

222

(, , )

BC relating the control

input

()uk to the height output

()yk

2012

() () () () ()yz GzGzGzuz

(29)

where

G is the transfer function relating the flow to

the height.

In this case, four possible fuzzy rules can be

derived, two of which are stated in the following:

• If

()

thr

∑

, then there is a

fault in

G ( subsystem 0) or

( subsystem 1) or in the flow-sensor,

• If

()

thr

∑

, then there is a

fault in

G ( subsystem 0) or

( subsystem 1) or

G ( subsystem 2) or

in the height-sensor (level-sensor).

The Kalman filter bank was evaluated under

different fault scenarios for an ON-OFF controller, a

P controller, and a PI controller, as shown in Fig.9.

0 50 100 150 200 250 300 350

100

200

300

time

height s

heights for fault -free and faulty cas es

0 50 100 150 200 250 300 350

-2

residual

time

residual

Figure 9: Kalman filter results for an On-Off and PI

Controller: for Flow and Height under various leakage

magnitudes.

Comments: The model of the fluid system is

nonlinear, complex and stochastic. A simplified

linearized model which contains only the dominant

poles (as it was difficult to identify the fast

dynamics) was used in the design of the Kalman

filter bank. Results from the evaluation on the

physical system shows that the Kalman filter bank is

robust in modelling uncertainties including

nonlinearities and neglected fast dynamics, while at

the same time being sensitive to incipient faults.

0 100 200 300 400 500 600 700 800 900

100

150

time

height

The height profile and the residual of Kalman filter

0 100 200 300 400 500 600 700 800 900

-15

-10

-5

time

residual

INTELLIGENT FAULT DIAGNOSIS USING SENSOR NETWORK

127

7 CONCLUSIONS

The proposed intelligent fault diagnostic scheme

based on a sequential integration of model-free and

model (Kalman)-based approach was found

promising when applied to a benchmarked

laboratory-scale two-tank system. The model-free

approach detects a presence of a possible fault from

the integration of both neural network and fuzzy

logic approaches. Results from the evaluation on the

physical system shows that the Kalman filter bank is

robust in modeling uncertainties including

nonlinearities and neglected fast dynamics, while

retaining its sensitivity to incipient faults. The

integration of fuzzy-logic and neural networks

proved itself to be a robust way of providing a quick

and reliable indication of a fault based on steady-

state measurements and height profile.

ACKNOWLEDGEMENTS

The authors wish to acknowledge the support of

KFUPM and the National Science and Engineering

Research Council (NSERC) of Canada, in carrying

out this work.

REFERENCES

S.X. Ding, “ Model-based Fault Diagnosis Techniques:

Design Schemes, Algorithms, and Tools” Springer-

Verlag 2008.

Silvio Simani, Cesare Fantuzzi and Ronald J Patton,

“Model-based Fault Diagnosis using Identification

Technique”, Advances in Industrial Control, Springer

Verlag, 2003.

Patton, R.J. Paul M. Frank, and Robert N. Clark, “Issues

in Fault Diagnosis for Dynamic Systems”, Springer-

Varlag, 2000.

Chen, J. and Patton, “Robust Model-based Fault Diagnosis

for Dynamic Systems”, Kluwer Academic Publishers,

1999.

Janos J. Gertler, “Fault Detection and Diagnosis in

Engineering Systems”, Marcel Dekker Inc, 1998.

R. Isermann, “ Fault diagnosis of Machines via parameter

estimation and knowledge processing”, Automatica,

Vol. 29, No.4, pp. 825-825, 1993.

R. Doraiswami, C.P.Diduch and Jiong Tang, “A

Diagnostic Model For Identifying Parametric Faults”,

IFAC World Congress, July 2008

R.Doraiswami, “Modelling and identification for fault

diagnosis: a new paradigm” Proceedings of the 10

International Conference on Control Applications,

September, 2001.

Marco Ferrente and Bruno Brunone, “Pipe system

diagnosis and leak detection by unsteady-state tests”,

Proceedings of the 7th World Congress on Intelligent

Control and Automation, Chongking, China, June 25-

27, 2008.

Zhang Sheng; Toshiyuki, A.; Shoji, H., “Gas leakage

detection system using Kalman filter”, 7th

International Conference on Signal Processing

Proceedings. ICSP '04, Volume 3, Aug31-Sept4.

2004, pp.:2533 - 2536

Doraiswami, R.; Sevenson, M.; Diduch, C.P

,”Autonomous control systems: monitoring, diagnosis

and tuning”, IEEE Transactions on Systems, Man and

Cybernetics, Part A, Volume 26, Issue 5, Sept.1996

pp. 646 – 655.

R.J. Patton, F.J. Uppal and C.J. Toribio, "Soft computing

approaches to fault diagnosis for dynamic systems: A

survey", in Proceedings of the IFAC Symposium

SAFEPROCESS 2000, Budapest-Hungary; 2000.

Astrom et.,al,” Control of Complex Systems”, Springer-

Verlag, 2001.

C. De Persis, “On the observability codistributions of a

nonlinear system” Systems and Control Letters,

Volume: 40, Issue: 5, August 15, 2000, pp. 297-304

H. Hammouri, P. Kabore, S.Othman, and J. Biston, J

“A. Failure diagnosis and nonlinear observer. Application

to a hydraulic process” Journal of The Franklin

Institute, Volume: 339, Issue: 4-5, July - August,

2002, pp. 455-478.

K.M. Kinnaert, “Robust fault detection based on observers

for bilinear systems”, Automatica, Volume: 35, Issue:

11, November, 1999, pp. 1829-1842.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

128