MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED

BROADBAND MIMO-BICM SCHEMES

Andreas Ahrens

Hochschule Wismar, University of Technology, Business and Design, Philipp-M¨uller-Straße 14, 23966 Wismar, Germany

C´esar Benavente-Peces

Universidad Polit´ecnica de Madrid, Ctra. Valencia. km. 7, 28031 Madrid, Spain

Keywords:

Multiple-Input Multiple-Output (MIMO) System, Wireless Transmission, EXIT Charts, Singular-Value De-

composition, Bit-Interleaved Coded Modulation (BICM), Iterative Decoding, Bit-Interleaved Coded Irregular

Modulation (BICIM), Spatial Division Multiplexing (SDM).

Abstract:

In this contribution we jointly optimize the number of activated MIMO layers and the number of bits per

symbol under the constraint of a given ﬁxed data throughput and integrity. In analogy to bit-interleaved coded

irregular modulation, we introduce a Broadband MIMO-BICM scheme, where different signal constellations

and mappings were used within a single codeword. Extrinsic information transfer (EXIT) charts are used for

analyzing and optimizing the convergence behaviour of the iterative demapping and decoding. Our results

show that in order to achieve the best bit-error rate, not necessarily all MIMO layers have to be activated.

1 INTRODUCTION

Iterative demapping and decoding aided bit-

interleaved coded modulation (BICM-ID) was

designed for bandwidth efﬁcient transmission over

fading channels (Caire et al., 1998; Chindapol, 2001).

The BICM philosophy has been extended by using

different signal constellations and bit-to-symbol

mapping arrangements within a single codeword,

leading to the concept of bit-interleaved coded

irregular modulation (BICIM) schemes, offering an

improved link adaptation capability and an increased

design freedom(Schreckenbach and Bauch, 2006).

Since the capacity of multiple-input multiple-output

(MIMO) systems increases linearly with the min-

imum number of antennas at both, the transmitter

as well as the receiver side, MIMO-BICM schemes

have attracted substantial attention (McKay and

Collings, 2005; Mueller-Weinfurtner, 2002) and

can be considered as an essential part of increasing

both the achievable capacity and integrity of future

generations of wireless systems (K¨uhn, 2006; Zheng

and Tse, 2003). However, their parameters have to be

carefully optimized, especially in conjunction with

adaptive modulation (Zhou et al., 2005). In general,

non-frequency selective MIMO links have attracted a

lot of research and have reached a state of maturity

(K¨uhn, 2006; Ahrens and Lange, 2008). By contrast,

frequency selective MIMO links require substantial

further research, where spatio-temporal vector coding

(STVC) introduced by RALEIGH seems to be an

appropriate candidate for broadband transmission

channels (Raleigh and Ciofﬁ, 1998; Raleigh and

Jones, 1999). In general, the choice of the number of

bits per symbol and the number of activated MIMO

layers combined with powerful error correcting codes

offer a certain degree of design freedom, which

substantially affects the performance of MIMO

systems. In addition to bit loading algorithms, in

this contribution the beneﬁts of channel coding are

also investigated. The proposed iterative decoder

structures employ symbol-by-symbol soft-output

decoding based on the Bahl-Cocke-Jelinek-Raviv

(BCJR) algorithm and are analyzed under the con-

straint of a ﬁxed data throughput (Bahl et al., 1974).

Against this background, the novel contribution of

this paper is that we jointly optimize the number of

activated MIMO layers and the number of bits per

symbol combined with powerful error correcting

codes under the constraint of a given ﬁxed data

throughput and integrity. Since the ”design-space”

is large, a two-stage optimization technique is

Ahrens A. and Benavente-Peces C. (2009).

MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED BROADBAND MIMO-BICM SCHEMES.

In Proceedings of the International Conference on Wireless Information Networks and Systems, pages 73-80

DOI: 10.5220/0002165800730080

 SciTePress

considered. Firstly, the uncoded spatial division

multiplexing (SDM) broadband MIMO scheme

is analyzed, investigating the allocation of both

the number of bits per modulated symbol and the

number of activated MIMO layers at a ﬁxed data rate.

Secondly, the optimized uncoded system is extended

by incorporating bit-interleaved coded modulation

using iterative detection (BICM-ID), whereby both

the uncoded as well as the coded systems are required

to support the same user data rate within the same

bandwidth.

This contribution is organized as follows: Section

2 introduces our system model, while the proposed

uncoded solutions are discussed in Section 3. In Sec-

tion 4 the channel encoded MIMO system is intro-

duced, while the computation of the EXIT transfer

function is presented in Section 5. The associated

performance results are presented and interpreted in

Section 6. Finally, Section 7 provides our concluding

remarks.

2 SYSTEM MODEL

When considering a frequency selective SDM MIMO

link, composed of n

transmit and n

receive anten-

nas, the block-oriented system is modelled by

u = H·c+ w . (1)

In (1), c is the (N

×1) transmitted signal vector con-

taining the complex input symbols transmitted over

transmit antennas in K consecutive time slots, i. e.,

= K n

. This vector can be decomposed into n

antenna-speciﬁc signal vectors c

according to

c =



,.. .,c

,... ,c



. (2)

In (2), the (K × 1) antenna-speciﬁc signal vector

transmitted by the transmit antenna µ (with µ =

1,.. ., n

) is modelled by



1µ

,... ,c

kµ

,... ,c

K µ



. (3)

The (N

×1) received signal vector u, deﬁned in (1),

can again be decomposed into n

antenna-speciﬁc

signal vectors u

(with ν = 1, ... ,n

) of the length

K + L

, i.e., N

= (K + L

, and results in

u =



,... ,u



. (4)

By taking the (L

+ 1) non-zero elements of the re-

sulting symbol rate sampled overall channel impulse

response between the µth transmit and νth receive an-

tenna into account, the antenna-speciﬁc received vec-

tor u

has to be extended by L

elements, compared to

the transmitted antenna-speciﬁc signal vector c

de-

ﬁned in (3). The ((K + L

) ×1) signal vector u

re-

ceived by the antenna ν (with ν = 1, ... ,n

) can be

constructed, including the extension through the mul-

tipath propagation, as follows



1ν

2ν

,... ,u

(K+L

)ν



. (5)

Similarly, in (1) the (N

×1) noise vector w results in

w =



,... ,w



. (6)

The vector w of the additive, white Gaussian noise

(AWGN) is assumed to have a variance of U

for both

the real and imaginary parts and can still be decom-

posed into n

antenna-speciﬁcsignal vectors w

(with

ν = 1,.. .,n

) according to



1ν

2ν

,... ,w

(K+L

)ν



. (7)

Finally, the (N

×N

) system matrix H of the block-

oriented system model, introduced in (1), results in

H =







... H

··· H







, (8)

and consists of n

single-input single-output

(SISO) channel matrices H

νµ

(with ν = 1,. .. ,n

and

µ = 1, ... ,n

). The system description, called spatio-

temporal vector coding (STVC), was introduced by

RALEIGH. Every of theses matrices H

νµ

with the di-

mension ((K +L

)×K) describes the inﬂuence of the

channel from transmit antenna µ to receive antenna ν

including transmit and receive ﬁltering. The channel

convolution matrix H

νµ

between the µth transmit and

νth receive antenna is obtained by taking the (L

+ 1)

non-zero elements of resulting symbol rate sampled

overall impulse response into account and results in:

νµ







0 0 ··· 0

0 ···

··· 0

. h

··· h

. h

··· h

0 h

. ··· h

0 0 h

···

0 0 0 ··· h







. (9)

Throughout this paper, it is assumed that the (L

+ 1)

channel coefﬁcients, between the µth transmit and νth

receive antenna have the same averaged power and

undergo a Rayleigh distribution. Furthermore, a block

fading channel model is applied, i.e., the channel is

WINSYS 2009 - International Conference on Wireless Information Networks and Systems

assumed to be time invariant for the duration of one

SDM MIMO data vector.

The interference between the different antenna’s

data streams, which is introduced by the off-diagonal

elements of the channel matrix H, requires appropri-

ate signal processing strategies. A popular technique

is based on the singular-value decomposition (SVD)

(Haykin, 2002) of the system matrix H, which can be

written as H = S·V·D

, where S and D

are unitary

matrices and V is a real-valued diagonal matrix of the

positive square roots of the eigenvalues of the matrix

H sorted in descending order

. The SDM MIMO

data vector c is now multiplied by the matrix D be-

fore transmission. In turn, the receiver multiplies the

received vector u by the matrix S

. Thereby neither

the transmit power nor the noise power is enhanced.

The overall transmission relationship is deﬁned as

y = S

(H·D·c+ w) = V·c+ ˜w. (10)

As a consequence of the processing in (10), the chan-

nel matrix H is transformed into independent, non-

interfering layers having unequal gains.

3 QUALITY CRITERIA

In general, the quality of data transmission can be in-

formally assessed by using the signal-to-noise ratio

(SNR) at the detector’s input deﬁned by the half ver-

tical eye opening and the noise power per quadrature

component according to

ρ =

(Half vertical eye opening)

Noise Power

)

, (11)

which is often used as a quality parameter (Ahrens

and Lange, 2008). The relationship between the

signal-to-noise ratio ρ = U

and the bit-error

probability evaluated for AWGN channels and M-ary

Quadrature Amplitude Modulation (QAM) is given

by (Proakis, 2000)

BER

log

(M)



1−

√



erfc





. (12)

When applying the proposed system structure, the

SVD-based equalization leads to different eye open-

ings per activated MIMO layer ℓ (with ℓ = 1,2, ··· ,L)

at the time k (with k = 1, 2,··· , K) within the SDM

MIMO signal vector according to

(ℓ,k)

ℓ,k

·U

sℓ

, (13)

The transpose and conjugate transpose (Hermitian) of

D are denoted by D

and D

, respectively.

where U

sℓ

denotes the half-level transmit amplitude

assuming M

ℓ

-ary QAM and

ℓ,k

represents the cor-

responding positive square roots of the eigenvalues of

the matrix H

H.Together with the noise power per

quadrature component, the SNR per MIMO layer ℓ at

the time k becomes

(ℓ,k)



(ℓ,k)



= ξ

ℓ,k

sℓ

)

. (14)

Using the parallel transmission over L ≤ min(n

)

MIMO layers, the overall mean transmit power be-

comes P

∑

ℓ=1

sℓ

, where the number of readily

separable layers

is limited by min(n

). Consider-

ing QAM constellations, the average transmit power

sℓ

per MIMO layer ℓ may be expressed as (Proakis,

2000)

sℓ

ℓ

−1) . (15)

Combining (14) and (15), the layer-speciﬁc SNR at

the time k results in

(ℓ,k)

= ξ

ℓ,k

2(M

ℓ

−1)

sℓ

. (16)

In order to transmit at a ﬁxed data rate while maintain-

ing the best possible integrity, i. e., bit-error rate, an

appropriate number of MIMO layers has to be used,

which depends on the speciﬁc transmission mode, as

detailed in Table 1. In general, the BER per SDM

MIMO data vector is dominated by the speciﬁc trans-

mission modes and the characteristics of the singu-

lar values, resulting in different BERs for the differ-

ent QAM conﬁgurations in Table 1. An optimized

adaptive scheme would now use the particular trans-

mission modes, e. g., by using bit auction procedures

(Wong et al., 1999), that results in the lowest BER

for each SDM MIMO data vector. This would lead to

different transmission modes per SDM MIMO data

vector and a high signaling overhead would result.

However, in order to avoid any signalling overhead,

ﬁxed transmission modes are used in this contribution

regardless of the channel quality. The MIMO layer

speciﬁc bit-error probability at the time k after SVD

is given by (Ahrens and Lange, 2008)

(ℓ,k)

BER



1−

√

ℓ



log

ℓ

)

erfc





(ℓ,k)





. (17)

The resulting average bit-error probability at the time

k assuming different QAM constellation sizes per ac-

It is worth noting that with the aid of powerful non-

linear near Maximum Likelihood (ML) sphere decoders it

is possible to separate n

> n

number of layers (Hanzo

and Keller, 2006).

MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED BROADBAND MIMO-BICM SCHEMES

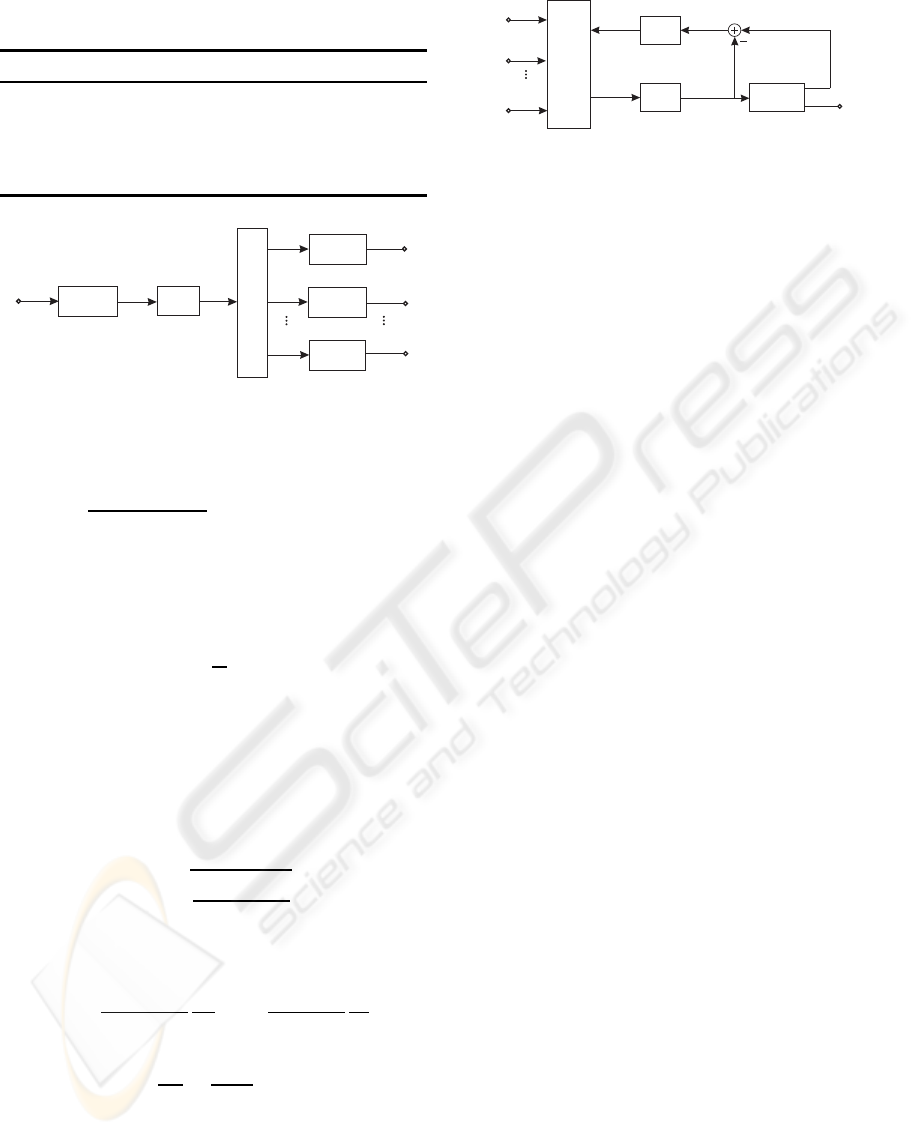
Table 1: Investigated transmission modes.

throughput layer 1 layer 2 layer 3 layer 4

8 bit/s/Hz 256 0 0 0

8 bit/s/Hz 64 4 0 0

8 bit/s/Hz 16 16 0 0

8 bit/s/Hz 16 4 4 0

8 bit/s/Hz 4 4 4 4

i b

1,k

2,k

L,k

encoder

∏

Mapper

1,k

2,k

L,k

MUX and Buffer

Figure 1: The channel-encoded MIMO transmitter’s struc-

ture.

tivated MIMO layer is given by

(k)

BER

∑

ν=1

log

)

∑

ℓ=1

log

ℓ

(ℓ,k)

BER

. (18)

Taking K consecutive time slots into account, needed

to transmit the SDM MIMO data vector, the aggre-

gate bit-error probability per SDM MIMO data vector

yields

BERblock

∑

k=1

(k)

BER

. (19)

When considering time-variant channel conditions,

rather than an AWGN channel, the BER can be de-

rived by considering the different transmission block

SNRs. Assuming that the transmit power is uniformly

distributed over the number of activated MIMO lay-

ers, i.e., P

sℓ

= P

/L, the half-level transmit amplitude

sℓ

per activated MIMO layer results in

sℓ

2L(M

ℓ

−1)

. (20)

Finally, the layer-speciﬁc signal-to-noise ratio at the

time k, deﬁned in (14), results together with (20) in

(ℓ,k)

= ξ

ℓ,k

2L(M

ℓ

−1)

= ξ

ℓ,k

L(M

ℓ

−1)

, (21)

with

. (22)

4 CODED MIMO SYSTEM

The transmitter structure including channel coding

is depicted in Figure 1. The encoder employs a

1,k

2,k

L,k

Soft Demapper

(ν)

(

∏

−1

∏

(ν)

a,1

(b)

decoder

(ν)

(i)

(ν)

(b)

(ν−1)

e,1

(b)

(ν)

a,2

(

Figure 2: Iterative demodulator structure.

half-rate nonrecursive, non-systematic (NSC) convo-

lutional code using the generatorpolynomials (7,5) in

octal notation. The uncoded information is organized

in blocks of N

bits, consisting of at least 3000 bits,

depending on the speciﬁc QAM constellation used.

Each data block i is encoded and results in the block

b consisting of N

= 2N

+ 4 encoded bits, includ-

ing 2 termination bits. The encoded bits are inter-

leaved using a random interleaver and stored in the

vector

b. The encoded and interleaved bits are then

mapped to the MIMO layers. The task of the mul-

tiplexer and buffer block of Figure 1 is to divide the

vector of encoded and interleaved information bits

into subvectors (

1,k

2,k

,··· ,

L,k

), each consisting

of 8 bits according to the chosen transmission mode

(Table 1). The individual binary data vectors

ℓ,k

are

then mapped to the QAM symbols c

ℓ,k

according to

the speciﬁc mapper used. The iterative demodulator

structure is shown in Figure 2 (Ahrens et al., 2008).

A detailed structure of the soft demapper structure is

portrayed in Figure 3. When using the iteration in-

dex ν, the ﬁrst iteration of ν = 1 commences with

the soft-demapper delivering the N

log-likelihood

ratios (LLRs) L

(ν=1)

(

b) of the encoded and inter-

leaved information bits, whose de-interleaved version

(ν=1)

a,1

(b) represents the input of the convolutionalde-

coder as depicted in Figure 2 (Bahl et al., 1974; K¨uhn,

2006). This channel decoder provides the estimates

(ν=1)

(i) of the original uncoded information bits as

well as the LLRs of the N

NSC-encoded bits in the

form of

(ν=1)

(b) = L

(ν=1)

a,1

(b) + L

(ν=1)

e,1

(b) . (23)

As seen in Figure 2 and (23), the LLRs of the

NSC-encoded bits consist of the receiver’s input sig-

nal itself plus the extrinsic information L

(ν=1)

e,1

(b),

which is generated by subtracting L

(ν=1)

a,1

(b) from

(ν=1)

(b). The appropriately ordered, i.e. inter-

leaved extrinsic LLRs are fed back as a priori in-

formation L

(ν=2)

a,2

(

b) to the soft demapper of Fig-

ure 2 for the second iteration. Following the de-

tailed structure of the soft-demapper in Figure 3, the

LLRs L

(ν)

(

b) are composed of the subvectors

(ν)

(

1,k

),L

(ν)

(

2,k

),··· , L

(ν)

(

L,k

)), each consist-

WINSYS 2009 - International Conference on Wireless Information Networks and Systems

ing of 8 elements according to the chosen transmis-

sion mode (Table 1). Each vector L

(ν)

(

ℓ,k

) is gener-

ated by the soft demapper from the MIMO channel’s

output y

ℓ,k

and the a-priori information L

(ν)

a,2

(

ℓ,k

) pro-

vided by the channel decoder. After the ﬁrst iteration,

this a-priori information emerges from the N

LLRs

(ν)

a,2

(

b), which are again decomposed into the subvec-

tors (L

(ν)

a,2

(

1,k

),L

(ν)

a,2

(

2,k

),··· , L

(ν)

a,2

(

L,k

)), each con-

sisting of 8 elements.

5 EXIT TRANSFER FUNCTION

Random variables (r.v.s) are denoted with capital let-

ters and their corresponding realizations with lower

case letters. Sequences of random variables and re-

alizations are indicated by boldface italics letters (as

B or b ). Furthermore, boldface roman letters denote

vectors (as B or b). The time instant is denoted with k

and the layer with ℓ. The transmitted data sequence B

is multiplexed onto the different used MIMO layers ℓ

and results in the MIMO layer speciﬁc sequence B

ℓ

with ℓ = 1, 2,. ..,L. The stationary binary input se-

quence B

ℓ

= [B

ℓ,1

ℓ,2

,... ,B

ℓ,k

,... ] consists of r.v.s

ℓ,k

, where the corresponding realizations b

ℓ,k

have

an index length of 1 bit and are taken from a ﬁnite

alphabet B = {0,1}. The mapper output sequence

ℓ

= [C

ℓ,1

ℓ,2

,... ,C

ℓ,k

,... ] on the ℓ-th layer consists

of r.v.s C

ℓ,k

, where the corresponding realizations c

ℓ,k

have an index length of log

ℓ

) bits and are taken

from a ﬁnite alphabet C = {0,1, ..., M

ℓ

−1}. The

symbols c

ℓ,k

are transmitted over independent chan-

nels resulting in the received values y

ℓ,k

. The a priori

channel, as depicted in Figure 4, models the a priori

information used at the soft demapper. The sequence

ℓ

= [A

ℓ,1

ℓ,2

,... ,A

ℓ,k

,... ] with the corresponding

realizations a

ℓ,k

contains the a priori LLR informa-

tion passed to the demapper. EXIT charts visualize

1,k

2,k

L,k

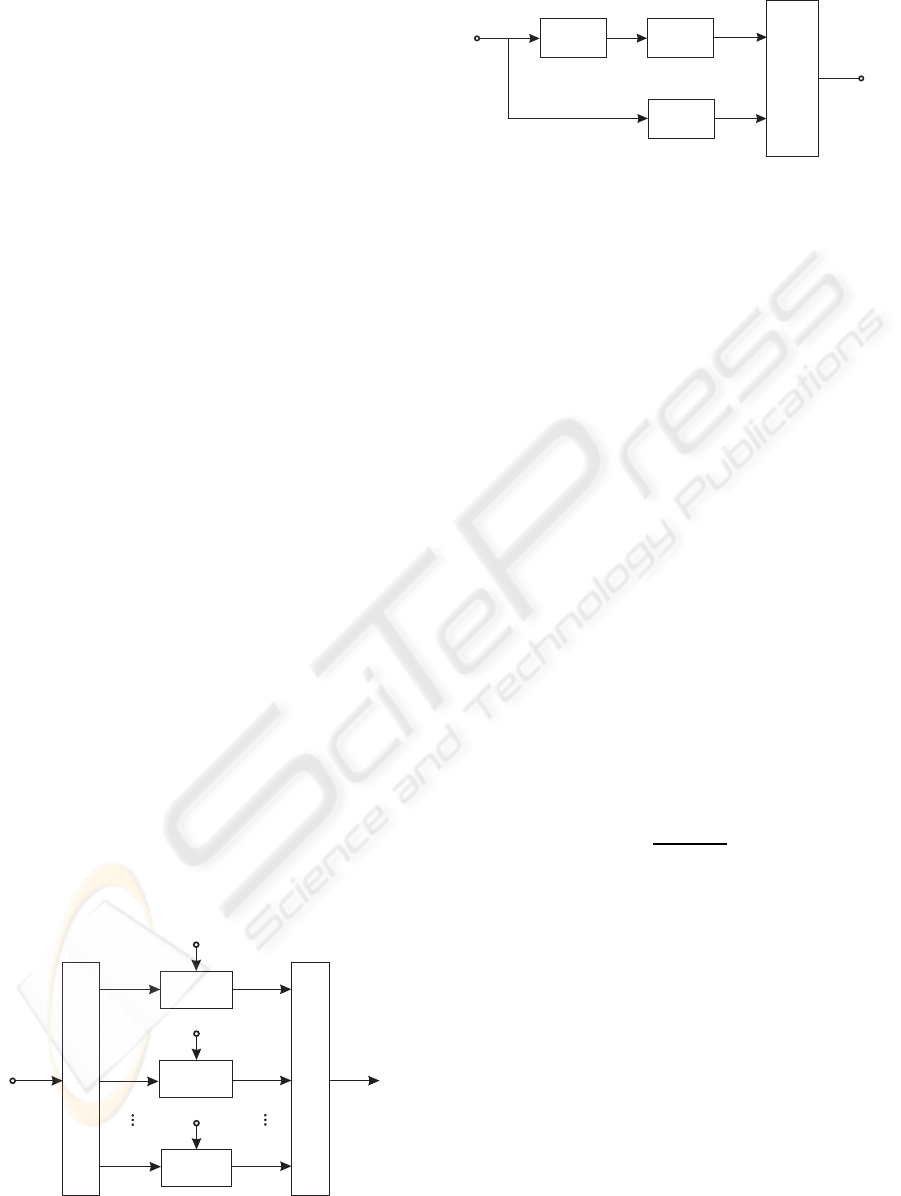
Soft-

Demapper

(ν)

(

1,k

)

(ν)

(

2,k

)

(ν)

(

L,k

)

(ν)

a,2

(

1,k

)

(ν)

a,2

(

2,k

)

(ν)

a,2

(

L,k

)

(ν)

(

(ν)

a,2

(

DEMUX and Buffer

MUX and Buffer

Figure 3: Detailed soft demapper demodulator structure.

ℓ,k

Mapper

Comm.

channel

A Priori

channel

Soft Demapper

Figure 4: Transmission model analyzing the ℓ-th MIMO

layer.

the input/output characteristics of the soft demap-

per and the decoder in terms of a mutual informa-

tion transfer between the data sequence B

ℓ

and the

sequence A

ℓ

of the a priori LLR information at the

input of the soft demapper, as well as between B

ℓ

and

the sequence E

ℓ

of the extrinsic LLR at the output, re-

spectively. Denoting the mutual information between

two r.v.s X and Y as I(X;Y) we may deﬁne for a given

sequence B

ℓ

the quantities I

ℓ,A

= I(A

ℓ

) as well

as I

ℓ,E

= I(E

ℓ

). Herein, I

ℓ,A

represents the aver-

age a priori information and I

ℓ,E

the average extrinsic

information, respectively (Ahrens et al., 2008). The

transfer characteristic T of the soft demapper is given

by I

ℓ,E

= T(I

ℓ,A

,ρ), where ρ represents the SNR of

the communication channel. Analyzing the outer de-

coder in a serially concatenated scheme T does not

depend on ρ. An EXIT chart is now obtained by plot-

ting the transfer characteristics T for both the demap-

per and the decoder within a single diagram, where

the axes have to be swapped for one of the constituent

decoders (Brink, 2001) (normally the outer one for

serial concatenation).

Analyzing the layer speciﬁc characteristics, a

MIMO-layer speciﬁc parameter α

(ℓ)

can be deﬁned

according to

(ℓ)

log

ℓ

)

, (24)

describing the fraction of the data sequence B that is

transmitted over the ℓth layer, i. e. B

ℓ

(Ahrens et al.,

2008). Therein, the parameter R describes the num-

ber of transmitted bits per time interval including all

L MIMO layers and results in R =

∑

ℓ=1

log

ℓ

Hence, the mutual information for a given sequence

B and the extrinsic LLR E at the output is obtained

I(E ;B ) =

∑

ℓ=1

(ℓ)

I(E

ℓ

) . (25)

The MIMO layer speciﬁc extrinsic LLR sequences

ℓ

are multiplexed onto the sequence E , which is

lead to the outer decoder (Ahrens et al., 2008). Ben-

eﬁcial values of α

(ℓ)

may be chosen by ensuring that

there is an open EXIT tunnel between the soft demap-

per transfer characteristic and the decoder transfer

MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED BROADBAND MIMO-BICM SCHEMES

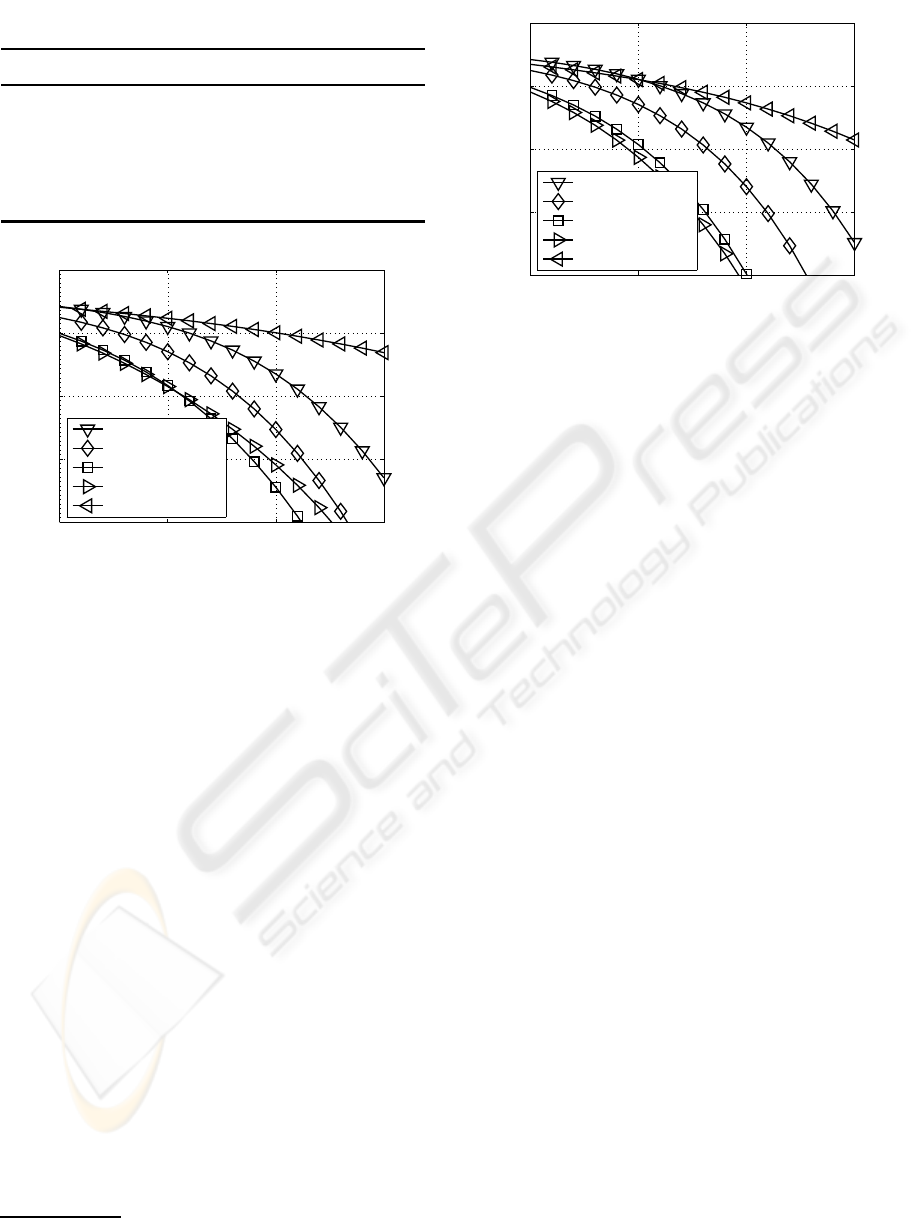
Table 2: Transmission modes and corresponding α

(ℓ)

,α

(1)

,α

(2)

,α

(3)

,α

8 bit/s/Hz 256, 1 0,0 0,0 0,0

8 bit/s/Hz 64, 3/4 4,1/4 0,0 0,0

8 bit/s/Hz 16,1/2 16, 1/2 0,0 0,0

8 bit/s/Hz 16,1/2 4,1/4 4,1/4 0,0

8 bit/s/Hz 4,1/4 4,1/4 4,1/4 4,1/4

10 15 20 25

−8

−6

−4

−2

10 ·lg(E

) (in dB) →

bit-error rate →

(256,0,0, 0) QAM

(64,4,0, 0) QAM

(16,16,0, 0) QAM

(16,4,4, 0) QAM

(4,4, 4,4) QAM

Figure 5: BER when using the transmission modes intro-

duced in Table 1 and transmitting 8 bit/s/Hz over frequency

selective channels with L

= 1.

characteristic at a given E

value that is close to

the channel capacity bound. Analyzing the transmis-

sion modes in Table 1, the resulting values of α

(ℓ)

are

shown in Table 2.

6 RESULTS

In this contributionﬁxed transmission modes are used

regardless of the channel quality. Assuming prede-

ﬁned transmission modes, a ﬁxed data rate can be

guaranteed. The obtained uncoded BER curves are

depicted in Figure 5 and 6 for the different QAM

constellation sizes and MIMO conﬁgurations of Ta-

ble 1, when transmitting at a bandwidth efﬁciency of

8 bit/s/Hz

. Assuming a uniform distribution of the

transmit power over the number of activated MIMO

layers, it turns out that not all MIMO layers have to

be activated in order to achieve the best BERs. More

explicitly, our goal is to ﬁnd that speciﬁc combination

of the QAM mode and the number of MIMO layers,

which gives the best possible BER performance at a

The expression lg(·) is considered to be the short form

of log

(·).

10 15 20 25

−8

−6

−4

−2

10 ·lg(E

) (in dB) →

bit-error rate →

(256,0,0, 0) QAM

(64,4,0, 0) QAM

(16,16,0, 0) QAM

(16,4,4, 0) QAM

(4,4, 4,4) QAM

Figure 6: BER when using the transmission modes intro-

duced in Table 1 and transmitting 8 bit/s/Hz over frequency

selective channels with L

= 4.

given ﬁxed bit/s/Hz bandwidth efﬁciency. However,

the lowest BERs can only be achieved by using bit

auction procedures leading to a high signalling over-

head. Analyzing the probability of choosing speciﬁc

transmission modes by using optimal bitloading as il-

lustrated in (Ahrens and Benavente-Peces, 2009) it

turns out that at moderate SNR only an appropriate

number of MIMO layers have to be activated, e. g.,

the (16,4, 4,0) QAM conﬁguration.

Using the half-rate constraint-length K

= 3 NSC

code, the BER performance is analyzed for an effec-

tive user throughput of 4 bit/s/Hz. The BER inves-

tigations using the NSC code are based on the best

uncoded schemes of Table 1. The information word

length is 3000 bits and a random interleaver is ap-

plied. In addition to the number of bits per symbol

and the number of activated MIMO layers, the achiev-

able performance of the iterative decoder is substan-

tially affected by the speciﬁc mapping of the bits to

both the QAM symbols as well as to the MIMO lay-

ers.

While the employment of the classic Gray-

mapping is appropriate in the absence of a priori

information, the availability of a priori information

in iterative receivers requires an exhaustive search

for ﬁnding the best non-Gray – synonymously also

referred to as anti-Gray – mapping scheme (Chin-

dapol, 2001). A mapping scheme optimized for per-

fect a priori information has usually a poor perfor-

mance, when there is no a priori information. How-

ever, when applying iterative demapping and decod-

ing, large gains can be achieved as long as the reli-

ability of the a priori information increases with the

number of iterations.

Analyzing the number of activated MIMO layers,

the soft-demappertransfer characteristics are depicted

in Figure 7 and 8 using anti-Gray mapping on all acti-

WINSYS 2009 - International Conference on Wireless Information Networks and Systems

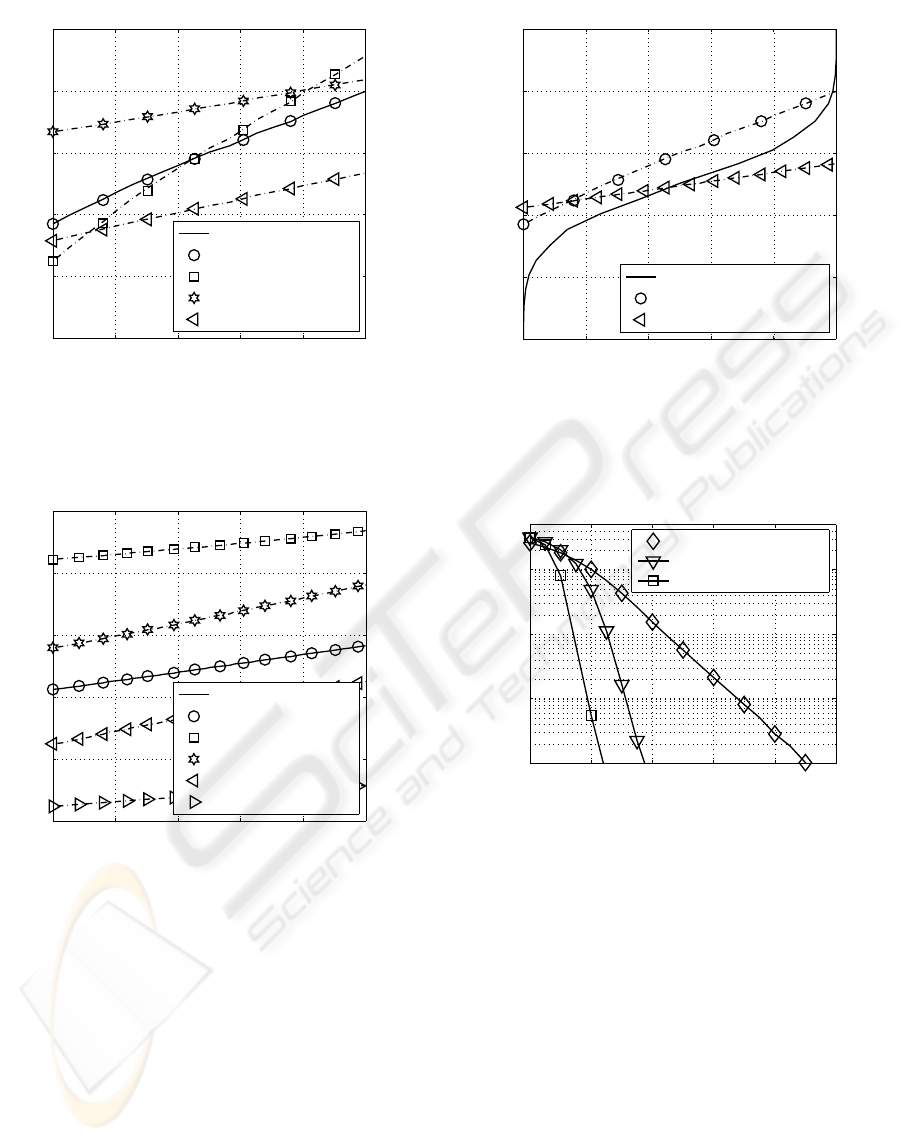
0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

extrinsic demapper output →

a-priori input →

I(E ;B ), Equa. (25)

I(E

), anti-Gray

I(E

), anti-Gray

I(E

), anti-Gray

I(E ;B ), Simulation

Figure 7: Layer-speciﬁc transfer characteristic when using

anti-Gray mapping and the (16,4,4,0) transmission mode

over frequency-selective MIMO links (10 log

) = 2

dB, L

= 1).

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

extrinsic demapper output →

a-priori input →

I(E ;B ), Equa. (25)

I(E

), anti-Gray

I(E

), anti-Gray

I(E

), anti-Gray

I(E

), anti-Gray

I(E ;B ), Simulation

Figure 8: Layer-speciﬁc transfer characteristic when using

anti-Gray mapping and the (4,4,4, 4) transmission mode

over frequency-selective MIMO links (10 log

) = 2

dB, L

= 1).

vated MIMO layers. Assuming predeﬁned QAM con-

stellation sizes, the entire soft demapper transfer char-

acteristic is well predictable by combining the single

MIMO layer transfer characteristics using the param-

eter α

(ℓ)

. Using predeﬁned QAM constellation sizes

and the corresponding α

(ℓ)

, the resulting EXIT chart

curve is depicted in Figure 9. In order to match the

soft demapper transfer characteristic properly to the

decoder transfer characteristic, a joint optimization of

the number of activated MIMO layers as well as the

number of bit per symbol has been carried out. Our

results suggest that not all MIMO layers have to be

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

extrinsic demapper output →

extrinsic decoder output →

NSC code

(16,4,4,0) QAM

(4,4,4,4) QAM

Figure 9: EXIT chart for an effective throughput of 4

bit/s/Hz when using anti-Gray mapping on all activated

MIMO layers (10 log

) = 2 dB and L

= 1) and the

half-rate NSC code with the generator polynomials of (7, 5)

in octal notation.

0 2 4 6 8 10

−4

−3

−2

−1

10 ·lg(E

) (in dB) →

bit-error rate →

(4,4, 4,4) QAM, 3 Iter.

(16,4, 4,0) QAM, 3 Iter.

(16,4, 4,0) QAM, 10 Iter.

Figure 10: BER for an effective user throughput of 4

bit/s/Hz (L

= 1) and anti-Gray mapping in combination

with different transmission modes and the half-rate NSC

code with the generator polynomials of (7,5) in octal no-

tation.

activated in order to shape the soft demapper transfer

characteristic properly. The best uncoded solutions

seems also to be useful in the coded scenario. The

corresponding BER curves are shown in Figure 10

and conﬁrm the EXIT charts results. In order to guar-

antee an efﬁcient information exchange between the

soft-dempapper and the decoder, i. e., an open EXIT

tunnel, only an appropriate number of MIMO layers

has to be activated. Using all MIMO layers for the

data transmission, the information exchange between

the soft-dempapper and the decoder stops relatively

early, as illustrated by the EXIT chart results in Fig-

ure 9, and signiﬁcant enhancements in the BER per-

formance can’t be achieved any longer by increasing

MODULATION-MODE ASSIGNMENT IN SVD-ASSISTED BROADBAND MIMO-BICM SCHEMES

the number of iterations at low SNR. As demonstrated

along this work, it is showed that an appropriate num-

ber of MIMO layers seems to be a promising solution

for minimizing the overall BER characteristic.

7 CONCLUSIONS

The choice of the number of bits per symbol and the

number of MIMO layers combined with error cor-

recting codes substantially affects the performance of

a MIMO system. Analyzing the uncoded system, it

turns out that not all MIMO layers have to be acti-

vated in order to achieve the best BERs. Considering

the coded system, the choice of the mapping strate-

gies combined with the appropriate number of acti-

vated MIMO layers and transmitted bits per symbol

offers a certain degree of design freedom, which sub-

stantially affects the performance of MIMO systems.

Here, using an appropriate number of MIMO layers

for the data transmission seems to be a promising so-

lution for minimizing the overall BER characteristic.

REFERENCES

Ahrens, A. and Benavente-Peces, C. (2009). Modulation-

Mode and Power Assignment in SVD-assisted Broad-

band MIMO Systems. In International Conference

on Wireless Information Networks and Systems (WIN-

SYS), Milan (Italy).

Ahrens, A. and Lange, C. (2008). Modulation-Mode and

Power Assignment in SVD-equalized MIMO Sys-

tems. Facta Universitatis (Series Electronics and En-

ergetics), 21(2):167–181.

Ahrens, A., Ng, S. X., K¨uhn, V., and Hanzo, L. (2008).

Modulation-Mode Assignment for SVD-Aided and

BICM-Assisted Spatial Division Multiplexing. Phys-

ical Communications (PHYCOM), 1(1):60–66.

Bahl, L. R., Cocke, J., Jelinek, F., and Raviv, J. (1974).

Optimal Decoding of Linear Codes for Minimizing

Symbol Error Rate. IEEE Transactions on Informa-

tion Theory, 20(3):284–287.

Brink, S. t. (2001). Convergence Behavior of Iteratively

Decoded Parallel Concatenated Codes. IEEE Trans-

actions on Communications, 49(10):1727–1737.

Caire, G., Taricco, G., and Biglieri, E. (1998). Bit-

Interleaved Coded Modulation. IEEE Transactions on

Information Theory, 44(3):927–946.

Chindapol, A. Ritcey, J. A. (2001). Design, Analysis, and

Performance Evaluation for BICM-ID with square

QAM Constellations in Rayleigh Fading Channels.

IEEE Journal on Selected Areas in Communications,

19(5):944–957.

Hanzo, L. and Keller, T. (2006). OFDM and MC-CDMA.

Wiley, New York.

Haykin, S. S. (2002). Adaptive Filter Theory. Prentice Hall,

New Jersey.

K¨uhn, V. (2006). Wireless Communications over MIMO

Channels – Applications to CDMA and Multiple An-

tenna Systems. Wiley, Chichester.

McKay, M. R. and Collings, I. B. (2005). Capacity

and Performance of MIMO-BICM with Zero-Forcing

Receivers. IEEE Transactions on Communications,

53(1):74– 83.

Mueller-Weinfurtner, S. H. (2002). Coding Approaches for

Multiple Antenna Transmission in Fast Fading and

OFDM. IEEE Transactions on Signal Processing,

50(10):2442–2450.

Proakis, J. G. (2000). Digital Communications. McGraw-

Hill, Boston.

Raleigh, G. G. and Ciofﬁ, J. M. (1998). Spatio-Temporal

Coding for Wirless Communication. IEEE Transac-

tions on Communications, 46(3):357–366.

Raleigh, G. G. and Jones, V. K. (1999). Multivariate

Modulation and Coding for Wireless Communication.

IEEE Journal on Selected Areas in Communications,

17(5):851–866.

Schreckenbach, F. and Bauch, G. (2006). Bit-Interleaved

Coded Irregular Modulation. European Transactions

on Telecommunications, 17(2):269–282.

Wong, C. Y., Cheng, R. S., Letaief, K. B., and Murch, R. D.

(1999). Multiuser OFDM with Adaptive Subcarrier,

Bit, and Power Allocation. IEEE Journal on Selected

Areas in Communications, 17(10):1747–1758.

Zheng, L. and Tse, D. N. T. (2003). Diversity and

Multiplexing: A Fundamental Tradeoff in Multiple-

Antenna Channels. IEEE Transactions on Information

Theory, 49(5):1073–1096.

Zhou, Z., Vucetic, B., Dohler, M., and Li, Y. (2005). MIMO

Systems with Adaptive Modulation. IEEE Transac-

tions on Vehicular Technology, 54(5):1073–1096.

WINSYS 2009 - International Conference on Wireless Information Networks and Systems