
DESIGN OF A NOVEL HYBRID OPTIMIZATION ALGORITHM
Dimitris V. Koulocheris and Vasilis K. Dertimanis
Vehicles Laboratory, National Technical University of Athens, Iroon Politechniou 9, 157 80, Athens, Greece
Keywords:
Hybrid optimization, Evolution strategy, Deterministic mutation, Line–search, Trust–region, Vehicles.
Abstract:
The interrelation of stochastic and deterministic optimization algorithms, as well as the exploitation of the ad-
vantages that each counterpart presents simultaneously, is studied in this paper. To this, a hybrid optimization
algorithm is developed, which consists of a conventional Evolution Strategy that maintains its recombination
and selection phases unaltered, while its mutation operator is replaced by well–known deterministic methods,
such as line–search and/or trust–region. The alteration results in superior performance of the novel algorithm,
compared to other instances of Evolutionary Algorithms, as exploited out in tests using Griewangk and Ras-
trigin functions. The proposed algorithm is further examined through its implementation to the structural
optimization problem of a full–car suspension model, with satisfying results.
1 INTRODUCTION
Numerical optimization, either deterministic (No-
cedal and Wright, 2006), or stochastic (Schwefel,
1995; Baeck, 1996), has shown to be a very pow-
erful tool in engineering, with implementation in a
very wide area of applications, including structural
design (Rao, 1996; Alkhatib et al., 2004; Koulocheris
et al., 2003a), system identification (Koulocheris
et al., 2003c), control (Fleming and Purshouse, 2002)
and fault diagnosis (Dertimanis, 2006; Chen and Pat-
ton, 1999).
The corresponding schemes that have been for a
long time the subject of significant research in the
field of numerical optimization, are mostly divided
into two main categories, deterministic and stochas-
tic: the former, usually build a local quadratic model
of the function of interest and converge rapidly to a
local stationary point, given a ”good initial guess”
for the parameter vector, while the latter perform in
a wide area of the search space, since, generally, the
optimization procedure is conducted in parallel. Yet,
both sufferfrom serious drawbacks, as the determinis-
tic methods depend drastically on the initial parameter
vector provided and frequently stuck in local optima,
while the stochastic ones present very slow conver-
gence rate (Vrazopoulos, 2003). To this, the idea of
combining the diverse characteristics of these two op-
timization categories into a hybrid algorithmic struc-
ture, follows naturally. Surprisingly, at least in the
engineering research field, relative works are rather
limited (Koulocheris et al., 2004), the almost exclu-
sive use of GA (refer to Appendix A for notation)
is utilized (Koh et al., 2003), while applications are
scarcely ever reported (Dertimanis et al., 2003). It
should be noted though, that the problem of acceler-
ating conventional EA has been faced using different
techniques, such as neural networks (Papadrakakis
and Lagaros, 2002).
This paper presents a methodology of intercon-
necting stochastic and deterministic optimization al-
gorithms, in a way that exploits the advantages of
both of them and results into a method that shows
faster convergence rate, as well as increased relia-
bility in the search for the global optimum. Among
EA, the stochastic component has been selected to
be the [µ/ρ (+/, ) λ]–ES, while the deterministic one
belongs to the family of quasi–Newton methods and
it is currently implemented using either line–search,
trust–region, or a combination of both. To this, the
currently proposed version of the algorithm integrates
previous ones (Koulocheris et al., 2008; Koulocheris
et al., 2004; Vrazopoulos, 2003), so that a more ro-
bust and flexible scheme is developed. In order to get
insight about the performance of the novel optimiza-
tion method, it is tested with the Griewangk and Ras-
trigin functions and compared with the conventional
ES (in fact its multi–membered plus and comma ver-
sions), as well as a meta version of EP (Baeck, 1996).
Consequently, it is applied to the problem of optimiz-
ing the characteristics of a suspension system used in
ground vehicles.
129
V. Koulocheris D. and K. Dertimanis V.
DESIGN OF A NOVEL HYBRID OPTIMIZATION ALGORITHM.
DOI: 10.5220/0002166501290135
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page
ISBN: 978-989-8111-99-9
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The rest of the paper is organized as follows: in
Sec. 2 the novel algorithm is presented and in Sec. 3,
indications of its performance are illustrated, through
the evaluation by theoretical objective functions, as
well as an application example, corresponding to the
problem of optimizing the riding comfort of a passen-
ger vehicle. In Sec. 4 some final remarks are given,
together with suggestions for further research.
2 THE HYBRID ALGORITHM
2.1 Description
The proposed hybrid algorithm with deterministic
mutation aims, as already mentioned, at interconnect-
ing the advantages of both optimization approaches.
Deterministic methods are characterized, if the opti-
mization function is regular, by a high convergence
rate and accuracy in the search for the optimum. On
the other hand, EA show a low convergence rate but
they can search on a significantly broader area for the
global optimum.
[µ/ρ (+/,) λ, ν]–hES is based on the distribu-
tion of the local and the global search for the opti-
mum and it consists of a super-positioned stochastic
global search, followed by a independent determinis-
tic procedure, which is activated under conditions in
specific members of the involved population. Thus,
every member of the population contributes in the
global search, while single individuals perform the
local search. Similar algorithmic structures, the theo-
retical backgroundof which pertains to the simulation
of insects societies (Monmarche et al., 2000; Rajesh
et al., 2001), have been presented by (Colorni et al.,
1996; Dorigo et al., 2000; Jayaraman et al., 2000).
The stochastic platform has been selected to be
the ES, while the deterministic counterpart is a quasi–
Newton algorithm (see Sec. 2.2). It must be noted that
the selection of ES among the other instances of EA is
justified via numerical experiments in non–linear pa-
rameter estimation problems (Schwefel, 1995; Baeck,
1996), which have provided significant indication that
ES perform better than the other two classes of EA,
namely GA and EP.
The conventional ES is based on three operators
that take on the recombination, the mutation and the
selection tasks. In order to maintain an adequate
stochastic performance in the new algorithm, the re-
combination and selection tasks are retained unal-
tered (refer to (Beyer and Schwefel, 2002) for a brief
discussion about the recombination phase), while its
strong local topology performance is utilized through
the substitution of the original mutation operator by a
quasi–Newton one.
A very important matter that affects significantly
the performance of the [µ/ρ (+/,) λ,ν]–ES involves
the members of the population that are selected for
mutation: there exist indications (Koulocheris et al.,
2003b) that the reason for the poor performance of
EA in non–linear multimodal functions is the loss of
information through the non-privileged individuals of
the population. Thus, the new deterministic mutation
operator is not applied to all λ recombined individu-
als but only to the ν worst among the (µ (+/,) λ),
where ν is an additional algorithm parameter. This
means that a sorting procedure takes place twice in
every iteration step: the first time in order to yield
the ν worst individuals and the second to support the
selection operator, which succeeds the new determin-
istic mutation operator. This modification enables the
strategy to yield the corresponding local optimum for
each of the selected ν worst individuals in every iter-
ation step. The advantage is reflected in terms of in-
creased convergence rate and reliability in the search
for the global optimum, while three other alternatives
were tested. In these, the deterministic mutation op-
erator was activated by:
- every individual of the involved population,
- a number of privileged individuals, and
- a number of randomly selected individuals.
The above alternatives led to three types of problem-
atic behavior. More specifically, the first increased the
computational cost of the algorithm without the desir-
able effect. The second alternative led to premature
convergence of the algorithm to local optima of the
objective function, while the third generated unstable
behavior that led to statistically low performance.
2.2 The Deterministic Mutation
As noted, quasi–Newton type methods replace the
original mutation of ES. Yet, unlike earlier ver-
sions (Vrazopoulos, 2003), it is not wise to limit
the operator in a line–search framework, since trust–
region and mixedcombined methods have also proven
to be competitive alternatives, or to enforce the exclu-
sive use of the BFGS Hessian update, as analytical or
finite–difference derivative information may, in some
cases, be either available, or costless to compute. This
fact leads to the optional implementation of full New-
ton methods, but the term quasi–Newton shall be pre-
served, in order to cover the majority of the problems
faced in practice. Thus, in the following it is assumed
that the gradient of the objective function is approx-
imated using finite–differences, while the Hessian is
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
130

calculated using the powerful BFGS update.
The currently presented version of the
[µ/ρ (+/,) λ,ν]–ES offers three alternatives to
be used as mutation operators, which are briefly
discussed in the following.
2.2.1 Line–search
A line–search algorithm is build in a simple idea: at
iteration k, given a descent direction p
k
, take a step
in that direction that yields an ”acceptable” parameter
vector, that is,
x
k+1
= x
k
+ λ
k
·p
k
(1)
for some λ
k
that makes x
k+1
an acceptable next iter-
ate. Since,
∇
2
f(x
k
)·p
k
= ∇f(x
k
) (2)
is utilized, the proposed mutation operator imple-
ments a cubic polynomial line–search procedure for
the determination of λ
k
, that satisfies both Wolfe con-
ditions (Nocedal and Wright, 2006). It must be noted
that in every iteration the full quasi–Newton step
(λ
k
= 1) is always tested first.
2.2.2 Trust–region
If in Eq. 1 the full quasi–Newton step is unsatisfac-
tory, it means that the quadratic model fails to approx-
imate the objective function in this region. Instead of
calculating a search direction, trust–region methods
calculate a shorter step length by solving the problem,
m
c
(x
k
+ p) = f(x
k
) + ∇f(x
k
)
T
·p (3)
+
1
2
p
T
∇
2
f(x
k
)·p
where m
c
is the quadratic model, subject to,
kpk ≤ δ
k
(4)
so that,
(∇
2
f(x
k
) + ξ·I)·p
k
= ∇f(x
k
) (5)
for some ξ > 0. Trust–region mutation utilizes two
alternatives for the calculation of ξ: the locally con-
strained optimal (”hook”) step and the double dogleg
step (Dennis and Schnabel, 1996).
2.2.3 Combined Trust–region / Line–search
The third alternative that the proposed algorithm of-
fers as mutation operator, is a combined trust–region
/ line–search framework. To this, Eqs. 3-5 are solved
approximately for the direction p
k
and if the full
quasi–Newton step does not result in a sufficient de-
crease of the objective function, a line–search is per-
formed, which guarantees, under certain conditions,
a lower objective function value. The corresponding
algorithm is described in (Nocedal and Yuan, 1998).
2.3 Termination Criteria
The termination criteria are distinguished as local, re-
ferring to the deterministic mutation and global, re-
ferring to [µ/ρ (+/,) λ,ν]–ES. For the former, stan-
dard tests that are presented in detail in (Nocedal and
Wright, 2006) and (Dennis and Schnabel, 1996) are
utilized:
- Objective function value smaller than a specified
tolerance,
- relative gradient norm less than a specified toler-
ance,
- relative distance between two successive itera-
tions less than a specified tolerance,
- not a descent current direction, and
- maximum mutation operator iterations exceeded.
In addition, the proposed algorithm terminates if at
least one of the following occurs:
- Absolute difference between worse and best ob-
jective function less than a specified tolerance,
- maximum function evaluations exceeded, and
- maximum iterations exceeded.
3 NUMERICAL RESULTS
3.1 Performance Evaluation
In order to assess the performance of the proposed al-
gorithm, a number N = 100 of independent tests were
utilized using the Griewangk
f(x) = 1+
n
∑
i=1
x
2
i
400·n
−
n
∏
i=1
cos
x
i
√
i
(6)
and the Rastrigin
f(x) = 10·n +
n
∑
i=1
x
2
i
−10·cos(2·π·x
i
) (7)
functions, with n = 50 parameters and known mini-
mum at x
m
= 0, f(x
m
) = 0. For the tests, a version
of the algorithm with µ = 15 parents and λ = 100 off-
spring was used, while the recombination type was
panmictic intermediate with ρ = 2 parents for the gen-
eration of each offspring. For the mutation, the trust–
region approach (using the double dogleg step) of the
relative operator was implemented and in every iter-
ation the ν = 3 worse vectors were mutated. The se-
lection was made among all the involved population
(that is both parents and offspring, choice that is de-
noted by the + sign of the full notation).
DESIGN OF A NOVEL HYBRID OPTIMIZATION ALGORITHM
131

Table 1: Statistical results of the compared methods: Griewangk’s function.
Termination Reason (%)
Method P P
min
P
max
Convergence Max. Iterations Mean CPU time (s)
(15+ 100,3)–hES −9.90 −10.06 −9.52 100 0 10
(15+ 100)–ES −0.10 −0.14 −0.06 0 100 28
(15,100)–ES −2.07 −2.83 −1.09 0 100 28
meta–EP −0.12 − 0.18 −0.09 0 100 25
Table 2: Statistical results of the compared methods: Rastrigin’s function.
Termination Reason (%)
Method P P
min
P
max
Convergence Max. Iterations Mean CPU time (s)
(15+ 100,3)–hES 1.14 0.00 2.05 100 0 5
(15+ 100)–ES 2.63 2.55 2.69 0 100 26
(15,100)–ES 2.56 2.35 2.66 0 100 26
meta–EP 2.59 2.52 2.62 0 100 24
Regarding the comparisons, two similar instances
of the conventional ES were used, that is the (15 +
100)–ES and the (15,100)–ES with panmictic re-
combination, while a version of the meta–EP with
100 population members and 10 random members for
comparison was activated. Taking under considera-
tion the possibility of a large spectrum of orders in the
final objective function value, the following quantity
was formulated,
P
j
= log
10
( f
final
), j = 1,...,100 (8)
and three statistics qualified the results, that is the
mean, the minimum and the maximum values of the
P
j
’s, out of the set of all the independent tests. I must
be noted in every iteration, that prior to the execu-
tion of every corresponding code, the random num-
ber generator was reset, in order to initialize all the
compared algorithms from the same population. As
far as the termination criteria are concerned, the tol-
erance for the convergence of the population and the
number of iterations were set equal to macheps
1/3
,
where macheps the computer precision, and 100, re-
spectively.
The results are illustrated in Tabs.1–2, where it is
clear that the hybrid algorithm has outperformed all
other EA. Indeed, the (15+ 100, 3)–hES with a trust–
region mutation returned the best statistics among the
four, while it converged in all the independent tests.
On the contrary, the EA didn’t managed to converge
within the specified number of iterations and required
2.5−5 times more CPU time in order to execute. Yet,
in the Rastrigin function the hybrid algorithm showed
premature convergence, an issue that requires further
investigation. In any case, the above resulted pro-
vide significant indication about the performance of
the novel algorithm and enforce its application to en-
gineering structural problems, as the one presented
next.
3.2 Application
The hybrid algorithm algorithm was subsequently ap-
plied to the problem of optimizing the performance
of a passenger vehicle, in order to improve the ride
comfort, under a vibration environment that gener-
ated vehicle–roadinteraction forces with certain spec-
tral characteristics, corresponding to the Draft–ISO
formulation (Cebon, 2000). To this, an equivalent
linear full–car model with seven degrees of freedom
was utilized, which is presented in Figs. 1(a)–1(b).
The objective was the optimization of the suspension
system under explicit structural and geometric con-
straints. Since a vibration environment was of inter-
est, the root–mean–square value of the vertical accel-
eration,
f(x) =
1
T
Z
T
0
¨x
2
M
(t)dt (9)
was selected as objective function, subject to the fol-
lowing constraints:
1. Parameter Bounds:
1000 ≤ k
s
ij
≤ 50000 (N/m) (10)
100 ≤ c
s
ij
≤ 5000 (N·s/m) (11)
for i = f,r and j = l,r.
2. Geometry:
|x
M
(t) + L
k
·θ
M
(t) + B
k
·φ
M
(t) −x
ij
(t)| ≤ 0.100m (12)
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
132
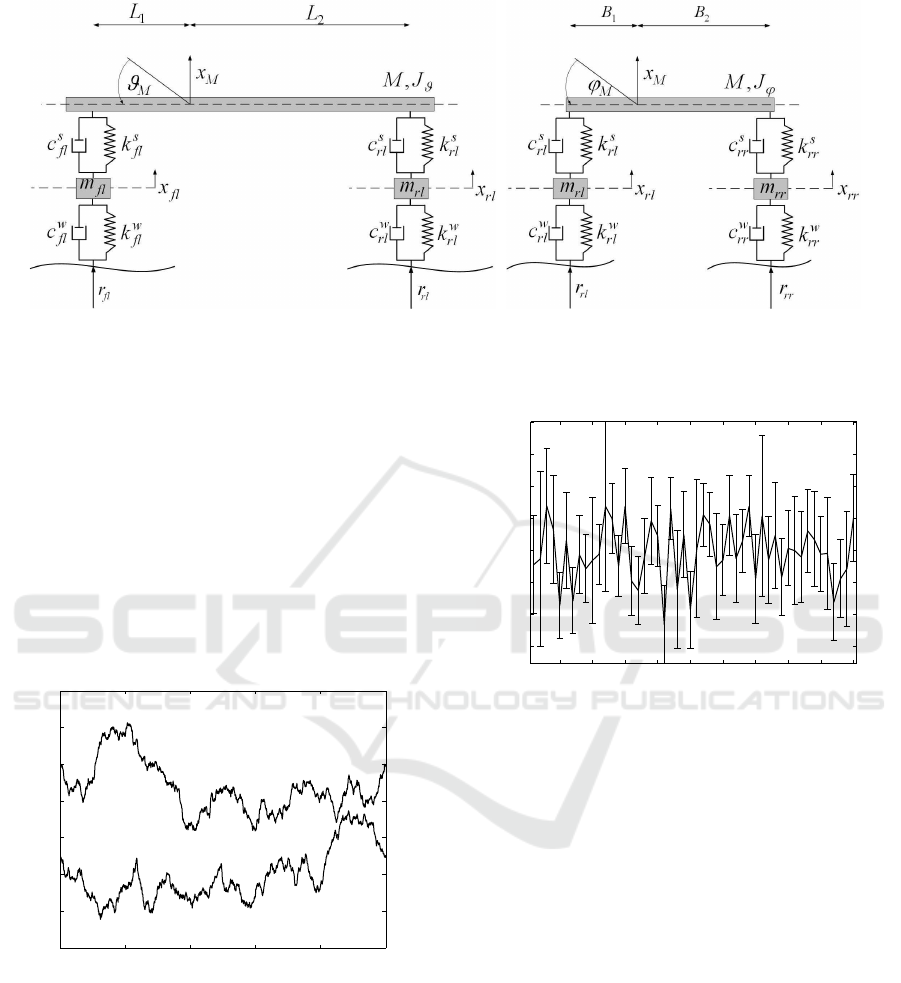
(a) (b)
Figure 1: Structural model of a passenger vehicle: (a) pitch–bounce view and (b) roll–bounce view.
|x
ij
(t)|−r
ij
(t)| ≤ 0.075m (13)
for k = 1, 2, i = f, r and j = l,r.
It can be proved (see (Rao, 1996) for details)
that a constrained optimization problem with low and
high bounds for the involved parameters can be trans-
formed into an unconstrained one, by applying a sim-
ple change of variable, a procedure that followedhere,
so that the penalty functions that were added in Eq. 9,
concerned only the second type of constraints.
0 20 40 60 80 100
−0.1
−0.08
−0.06
−0.04
−0.02
0
0.02
0.04
Left (upper) and right (lower) road profiles
r [m]
Distance [m]
Figure 2: Two tracks across an ”average” isotropic surface.
Algorithms’s performance characteristics were
examined via 50 Monte–Carlo experiments, each one
consisting of a certain profile realization (see Fig. 2
for a single realization of the road surface topogra-
phy) and 20 independent tests, for the same version
of the algorithm as before, that is the (15 + 100,3)–
hES.
The results are displayed in Figs. 3–4. Figure 3
displays the performance of the objective function in
5 10 15 20 25 30 35 40 45 50
0.37
0.38
0.39
0.4
0.41
0.42
0.43
0.44
Monte Carlo experiment
Objective function’s performance
f(x)
Figure 3: Mean value and dispersions of the objective func-
tion, with respect to the Monte Carlo experiments.
every Monte Carlo experiment. The horizontal line
refers to the mean value of the 20 independent tests,
while the vertical lines to the standard deviation of
the 20 values of every Monte–Carlo experiment. It
appears that the hybrid algorithm presented high sta-
tistical consistency, fact that is further supported by
the suspension results that are illustrated in Fig. 4,
from which clear suggestions about the front/rear sus-
pension set up can be made. Yet, the relatively high
standard deviations of the suspensions’ stiffness indi-
cate that more intuition is required about the role of
these structural parameters to the root–mean–square
acceleration, with respect to the mathematical model.
4 CONCLUSIONS
A novel hybrid optimization method was presented
in this paper, which attempts to combine the diverse
characteristics of deterministic and stochastic opti-
DESIGN OF A NOVEL HYBRID OPTIMIZATION ALGORITHM
133
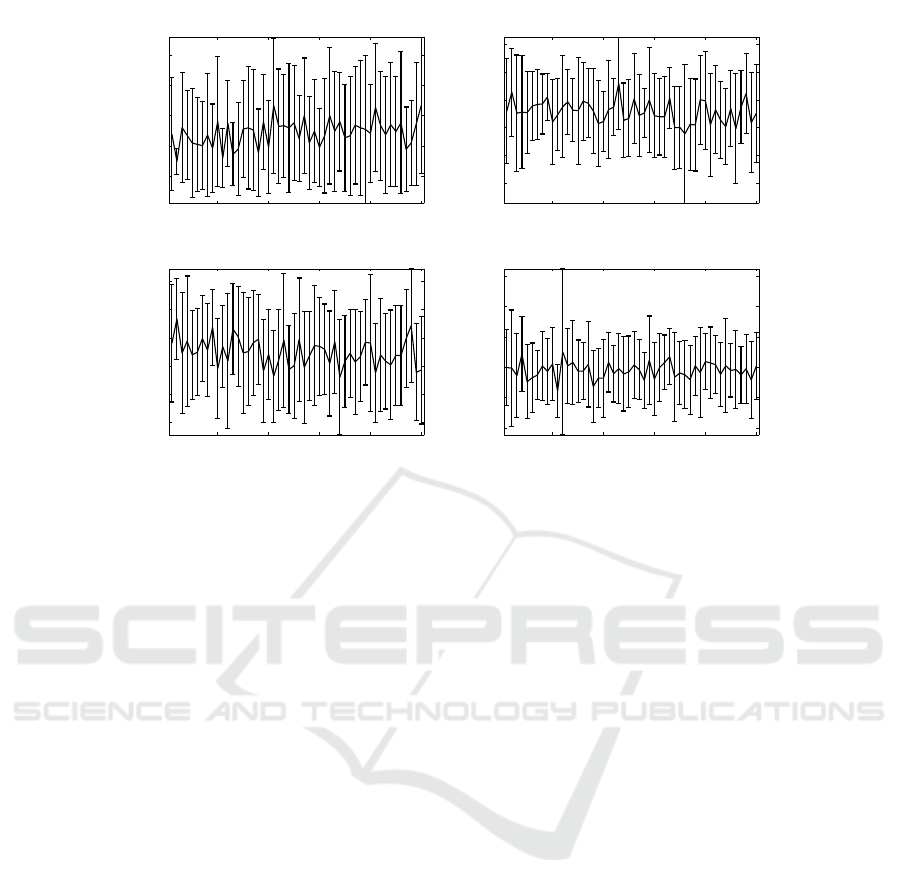
10 20 30 40 50
0.5
1
1.5
2
2.5
x 10
4
Monte Calro experiment
Front Stiffness
k
f
[N/m]
10 20 30 40 50
1600
1800
2000
2200
2400
2600
Monte Carlo experiment
Front Damping
c
f
[Ns/m]
10 20 30 40 50
0.5
1
1.5
2
2.5
3
x 10
4
Monte Carlo experiment
Rear Stiffness
k
r
[N/m]
10 20 30 40 50
1200
1400
1600
1800
2000
2200
Monte Carlo experiment
Rear Damping
c
r
[Ns/m]
Figure 4: Mean value and dispersions of the parameter vector, with respect to the Monte Carlo experiments.
mization algorithms. That is, to interconnect fast lo-
cal convergence and increased reliability in the search
of the global optimum, without depending on initial
values, or suffer from low convergence rate. To this,
the corresponding scheme that was developed main-
tains the stochastic kernel of ES and replaces the orig-
inal mutation operator by relative methods that utilize
derivative information and act on the non-privileged
population members, resulting in a more efficient per-
formance.
The proposed algorithm was compared to conven-
tional instances of EA using standard test functions,
such as the Griewangk and Rastrigin ones, showing
significant evidenceabout its performance,and subse-
quently was applied to the problem of optimizing the
performance of a passenger vehicle with satisfying re-
sults that suggest, not only its use in other engineering
problems, but also further investigation about its de-
sign parameters, as well as the user–supplied controls.
REFERENCES
Alkhatib, R., Nakhaie Jazarb, G., and Golnaraghi, M.
(2004). Optimal design of passive linear suspension
using genetic algorithm. Journal of Sound and Vibra-
tion, 275(3–5):665–691.
Baeck, T. (1996). Evolutionary Algorithms in Theory and
Practice. Oxford University Press, New York.
Beyer, H. and Schwefel, H. (2002). Evolution Strategies:
a comprehensive introduction. Natural Computing,
1(1):3–52.
Cebon, D. (2000). Handbook of Vehicle–Road Interaction.
Swets & Zeitlinger, Lisse.
Chen, J. and Patton, R. (1999). Robust model–based fault
diagnosis of dynamic systems. Kluwer Academic Pub-
lishers, Massachusetts.
Colorni, A., Dorigo, M., Maffioli, F., Maniezzo, V., Righini,
G., and Trubian, M. (1996). Heuristics from nature for
hard combinatorial optimization problems. Interna-
tional Transactions on Operational Research, 3(1):1–
21.
Dennis, J. and Schnabel, R. (1996). Numerical Methods
for Unconstrained Optimization and Nonlinear
Equations. Society for Industrial and Applied Mathe-
matics, Philadelphia.
Dertimanis, V. (2006). Fault Modeling and Identification
in Mechanical Systems. PhD thesis, School of Me-
chanical Engineering, GR 157 80 Zografou, Athens,
Greece. In greek.
Dertimanis, V., Koulocheris, D., Vrazopoulos, H., and Ka-
narachos, A. (2003). Time–series parametric model-
ing using Evolution Strategy with deterministic mu-
tation operators. In Proceedings of the International
Conference on Intelligent Control Systems and Signal
Processing, pages 328–333, Faro, Portugal. IFAC.
Dorigo, M., Bonabeau, E., and Theraulaz, G. (2000). Ant
algorithms and stigmergy. Future Generation Com-
puter Systems, 16(8):851–871.
Fleming, P. and Purshouse, R. (2002). Evolutionary algo-
rithms in control systems engineering: a survey. Con-
trol Engineering Practice, 10(11):1223–1241.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
134

Jayaraman, V., Kulkarni, B., Karale, S., and Shelokar, P.
(2000). Ant colony framework for optimal design and
scheduling of batch plants. Computers and Chemical
Engineering, 24(8):1901–1912.
Koh, C., Chen, Y., and Liaw, C.-Y. (2003). A hybrid com-
putational strategy for identification of structural pa-
rameters. Computers & Structures, 81(2):107–117.
Koulocheris, D., Dertimanis, V., and Spentzas, C. (2008).
Parametric identification of vehicle structural charac-
teristics. Forschung im Ingenieurwesen, 72(1):39–51.
Koulocheris, D., Vrazopoulos, H., and Dertimanis, V.
(2003a). Design of an I-Beam using a determinis-
tic Multiobjective optimization algorithm. WSEAS
Transactions On Circuits & Systems, 2(4):794–799.
Koulocheris, D., Vrazopoulos, H., and Dertimanis, V.
(2003b). Hybrid Evolution Strategy for the design
of welded beams. In Proceedings of EUROGEN,
Barcelona, Spain.
Koulocheris, D., Vrazopoulos, H., and Dertimanis, V.
(2003c). Vehicle Suspension system identification us-
ing Evolutionary Algorithms. In Proceedings of EU-
ROGEN, Barcelona, Spain.
Koulocheris, D., Vrazopoulos, H., and Dertimanis, V.
(2004). A Hybrid Evolution Strategy for vehicle sus-
pension optimization. WSEAS Transactions On Sys-
tems, 3(1):90–95.
Monmarche, N., Venturini, G., and Slimane, M. (2000).
On how Pachycondyla apicalis ants suggest a new
search algorithm. Future Generation Computer Sys-
tems, 16(8):937–946.
Nocedal, J. and Wright, S. (2006). Numerical Optimization.
Springer–Verlag, New York, 2
nd
edition.
Nocedal, J. and Yuan, Y. (1998). Combining trust region
and line search techniques. In Yan, Y., editor, Ad-
vances in Nonlinear Programming, pages 153–175.
Kluwer Academic Publishers.
Papadrakakis, M. and Lagaros, N. (2002). Reliability–
based structural optimization using neural networks
and Monte Carlo simulation. Computer methods in
applied mechanics and engineering, 191(32):3491–
3507.
Rajesh, J., Gupta, S., Rangaiah, G., and Ray, A. (2001).
Multi–objective optimization of industrial hydrogen
plants. Chemical Engineering Science, 56(3):999–
1010.
Rao, S. (1996). Engineering Optimization: Theory and
Practice. John Wiley & Sons Ltd., New York, 3
rd
edition.
Schwefel, H. (1995). Evolution & Optimum Seeking. John
Wiley & Sons Ltd., New York.
Vrazopoulos, H. (2003). New Optimization Methods of
Mechanical Systems. PhD thesis, School of Me-
chanical Engineering, GR 157 80 Zografou, Athens,
Greece. in greek.
APPENDIX A: NOTATION
µ number of parent population
ρ number of recombination population
λ number of offspring
ν number of mutation population
(+/,) plus / comma version of ES
EA Evolutionary Algorithms
ES Evolution Strategy
EP Evolutionary Pogramming
GA Genetic Algorithms
hES hybrid Evolution Strategy
DESIGN OF A NOVEL HYBRID OPTIMIZATION ALGORITHM
135
