
A PRACTICAL STEREO SYSTEM BASED ON REGULARIZATION
AND TEXTURE PROJECTION
Federico Tombari
1,2
and Kurt Konolige
1
1
Willow Garage Inc., Menlo Park, CA, U.S.A.
2
DEIS - ARCES, University of Bologna, Italy
Keywords:
Stereo vision, Spacetime stereo, Robot vision.
Abstract:
In this paper we investigate the suitability of stereo vision for robot manipulation tasks, which require high-
fidelity real-time 3D information in the presence of motion. We compare spatial regularization methods for
stereo and spacetime stereo, the latter relying on integration of information over time as well as space. In both
cases we augment the scene with textured projection, to alleviate the well-known problem of noise in low-
textured areas. We also propose a new spatial regularization method, local smoothing, that is more efficient
than current methods, and produces almost equivalent results. We show that in scenes with moving objects
spatial regularization methods are more accurate than spacetime stereo, while remaining computationally sim-
pler. Finally, we propose an extension of regularization-based algorithms to the temporal domain, so to further
improve the performance of regularization methods within dynamic scenes.
1 INTRODUCTION
As part of the Personal Robot project at Willow
Garage, we are interested in building a mobile robot
with manipulators for ordinary household tasks such
as setting or clearing a table. An important sensing
technology for object recognition and manipulation is
short-range (30cm – 200cm) 3D perception. Criteria
for this device include:
• Good spatial and depth resolution (1/10 degree, 1
mm).
• High speed (>10 Hz).
• Ability to deal with moving objects.
• Robust to ambient lighting conditions.
• Small size, cost, and power.
Current technologies fail on at least one of these cri-
teria. Flash ladars (Anderson et al., 2005) lack depth
and, in some cases, spatial resolution, and have non-
gaussian error characteristics that are difficult to deal
with. Line stripe systems (Curless and Levoy, 1995)
have the requisite resolution but cannot achieve 10
Hz operation, nor deal with moving objects. Struc-
tured light systems (Salvi et al., 2004) are achieving
reasonable frame rates and can sometimes incorporate
motion, but still rely on expensive and high-powered
projection systems, while being sensitive to ambient
illumination and object reflectance. Standard block-
matching stereo, in which small areas are matched be-
tween left and right images (Konolige, 1997), fails on
objects with low visual texture.
An interesting and early technology is the use
of stereo with unstructured light (Nishihara, 1984).
Unlike structured light systems with single cameras,
stereo does not depend on the relative geometry of
the light pattern – the pattern just lends texture to the
scene. Hence the pattern and projector can be simpli-
fied, and standard stereo calibration techniques can be
used to obtain accurate 3D measurements.
Even with projected texture, block-matching
stereo still forces a tradeoff between the size of the
match block (larger sizes have lower noise) and the
precision of the stereo around depth changes (larger
sizes “smear” depth boundaries). One possibility is
to use smaller matching blocks, but reduce noise by
using many frames with different projection patterns,
thereby adding information at each pixel. This tech-
nique is known as Spacetime Stereo (STS) (Davis
et al., 2005),(Zhang et al., 2003). It produces out-
standing results on static scenes and under controlled
illumination conditions, but movingobjects create ob-
vious difficulties (see Figure 1, bottom-left). While
there have been a few attempts to deal with mo-
tion within a STS framework (Zhang et al., 2003),
(Williams et al., 2005), the results are either compu-
5
Tombari F. and Konolige K.
A PRACTICAL STEREO SYSTEM BASED ON REGULARIZATION AND TEXTURE PROJECTION.
DOI: 10.5220/0002167800050012
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page
ISBN: 978-989-674-000-9
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: The top figure shows the disparity surface for
a static scene; disparities were computed by integrating
over 30 frames with varying projected texture using block-
matching (3x3x30 block). The bottom-left figure is the
same scene with motion of the center objects, integrated
over 3 frames (5x5x3 block). The bottom-right figure is
our local smoothing method for a single frame (5x5 block).
tationally expensive or perform poorly, especially for
fast motions and depth boundaries.
In this paper, we apply regularization methods to
attack the problem of motion in spacetime stereo.
One contribution we propose is to enforce not only
spatial, but also temporal smoothness constraints that
benefit from the texture-augmented appearance of the
scene. Furthermore, we propose a new regularization
method, local smoothing, that yields an interesting
efficiency-accuracy trade-off. Finally, this paper also
aims at comparing STS with regularization methods,
since a careful reading of the spacetime stereo liter-
ature (Davis et al., 2005; Zhang et al., 2003) shows
that this has not been addressed before. Experimen-
tally we found that, using a projected texture, regu-
larization methods applied on single frames perform
better than STS on dynamic scenes (see Figure 1) and
produces interesting results also on static scenes.
In the next section we review several standard reg-
ularization methods, and introduce our novel method,
local smoothness, which is more efficient and almost
as effective. We then show how regularization can be
applied across time as well as space, to help alleviate
the problem of object motion in STS. In the experi-
mental section, the considered methods are compared
on static scenes and in the presence of moving objects.
2 SMOOTHNESS CONSTRAINTS
IN STEREO MATCHING
Stereo matching is difficult in areas with low tex-
ture and at depth boundaries. Regularization meth-
ods add a smoothness constraint to model the reg-
ularity of surfaces in the real world. The general
idea is to penalize those candidates lying at a differ-
ent depth from their neighbors. A standard method
is to construct a disparity map giving the probability
of each disparity at each pixel, and compute a global
energy function for the disparity map as a multi-class
Pairwise Markov Random Field. The energy is then
minimized using approximate methods such as Belief
Propagation (BP) (Klaus et al., 2006), (Yang, 2006)
or Graph Cuts (GC) (Kolmogorov and Zabih, 2001).
Even though efficient BP-based algorithms have been
proposed (Yang et al., 2006), (Felzenszwalb and Hut-
tenlocher, 2004), overall the computational load re-
quired by global approaches does not allow real-time
implementation on standard PCs.
Rather than solving the full optimization prob-
lem over the disparity map, scanline methods en-
force smoothness along a line of pixels. Initial ap-
proaches based on Dynamic Programming (DP) and
Scanline Optimization (SO) (Scharstein and Szeliski,
2002) use only horizontal scanlines, but suffer from
streaking effects. More sophisticated approaches
apply SO over multiple, variably-oriented scanlines
(Hirschmuller, 2005) or use multiple horizontal and
vertical passes (Kim et al., 2005), (M. Bleyer, 2008),
(Gong and Yang, 2005). These methods tend to be
faster than global regularization, though the use of
several DP or SO passes tends to increase the com-
putational load of the algorithms.
Another limit to the applicability of these ap-
proaches within a mobile robotic platform is their
fairly high memory requirements. This section we re-
view scanline methods and proposes a new method
called local smoothness.
2.1 Global Scanline Methods
Let I
L
, I
R
be a rectified stereo image pair sized M · N
and W(p) a vector of points belonging to a squared
window centered on p. The standard block-matching
stereo algorithm computes a local cost C(p, d) for
each point p ∈ I
L
and each possible correspondence
at disparity d ∈ D on I
R
:
C(p, d) =
∑
q∈W(p)
e(I
L
(q), I
R
(δ(q, d))). (1)
where δ(q, d) is the function that offsets q in I
R
ac-
cording to the disparity d, and e is a (dis)similarity
function. A typical dissimilarity function is the L
1
distance:
e(I
L
(q), I
R
(δ(q, d))) = |I
L
(q) − I
R
(δ(q, d))|. (2)
In this case, the best disparity for point p is selected
as:
d
∗
= argmin
d
{C(p, d)}. (3)
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
6

In the usual SO or DP-based framework, the global
energy functional being minimized along a scanline S
is:
E (d(·)) =
∑
p∈S
C(p, d(p)) +
∑
p∈S
∑
q∈N (p)
ρ(d(p), d(q))
(4)
where d(·) denotes now a function that picks out a
disparity for its pixel argument, and q ∈ N (p) are the
neighbors of p according to a pre-defined criterion.
Thus to minimize (4) one has to minimize two differ-
ent terms, the first acting as a local evidence and the
other enforcing smooth disparity variations along the
scanline, resulting in a non-convexoptimization prob-
lem. The smoothness term ρ is usually derived from
the Potts model (Potts, 1995):
ρ(d(p), d(q)) =
0 d(p) = d(q)
π d(p) 6= d(q)
(5)
π being a penalty term inversely proportional to the
temperature of the system. Usually for stereo a Mod-
ified Potts model is deployed, which is able to han-
dle slanted surfaces by means of an additional penalty
term π
s
<< π:
ρ(d(p), d(q)) =
0 d(p) = d(q)
π
s
|d(p) − d(q)| = 1
π elsewhere
(6)
Thanks to (6), smooth variations of the disparity
surface are permitted at the cost of the small penalty
π
s
. Usually in SO and DP-based approaches the set
of neighbours for a point p includes only the previ-
ous point along the scanline, p
−1
. From an algorith-
mic perspective, an aggregated cost A(p, d) has to be
computed for each p ∈ S, d ∈ D:
A(p, d) = C(p, d) + min
d
′
{A(p
−1
, d
′
) + ρ(d,d
′
)} (7)
Because of the nature of (7) the full cost for each
disparity value at the previous point p
−1
must be
stored in memory. If a single scanline is used, this
typically requires O(M · D) memory, while if mul-
tiple passes along non-collinear scanlines are con-
cerned, this usually requires O(M · N · D) memory
(Hirschmuller, 2005).
2.2 Local Smoothness
Keeping the full correlation surface over M · N · D is
expensive; we seek a more local algorithm that ag-
gregates costs incrementally. In a recent paper (Zhao
and Katupitiya, 2006), a penalty term is added in a lo-
cal fashion to improve post-processing of the dispar-
ity image based on left-right consistency check. Here,
we apply a similar penalty during the construction of
the disparity map and generalize its use for multiple
scanlines. Given a scanline S, we can modify (7) as
follows:
A
LS
(p, d) = C(p, d) + ρ(d,
˜
d) (8)
where
˜
d = argmin
d
{C(p
−1
, d)} (9)
is the best disparity computed for the previous point
along the scanline. Hence, each local cost is penalized
if the previously computed correspondence along the
scanline corresponds to a different disparity value. In
this approach, there is no need to keep track of an ag-
gregated cost array, since the aggregated cost for the
current point only depends on the previously com-
puted disparity. In practice the computation of (8)
for the current disparity surface might be performed
simply by subtracting π from C(p,
˜
d) and π− π
s
from
C(p,
˜
d − 1), C(p,
˜
d + 1).
Enforcing smoothness in just one direction helps
handle low-textured surfaces, but tends to be inaccu-
rate along depth borders, especially in the presence of
negative disparity jumps. Using two scans, e.g. hori-
zontally from left to right and from right to left, helps
to reduce this effect, but suffers from the well-known
streaking effect (Scharstein and Szeliski, 2002). In or-
der to enforce inter-scanline consistency, we run local
smoothness over 4 scans, 2 vertical and 2 horizontal
(see Figure 8). In this case, which we will refer to as
Spatial Local Smoothness (LS
s
), the aggregated cost
(8) is modified as follows:
A
LS
s
(d) = C(p, d) +
∑
q∈N (p)
ρ(d, d(q)). (10)
Here N refers to the 4 disparities previously com-
puted on p. The computation of d
∗
benefits from
propagated smoothness constraints from 4 different
directions, which reduces noise in low-textured sur-
faces, and also reduces streaking and smearing effects
typical of scanline-based methods.
It is worth pointing out that the LS
s
approach can
be implemented very efficiently by means of a two-
stage algorithm. In particular, during the first stage
of the algorithm, the forward-horizontal and forward-
vertical passes are computed, and the result
is stored into two M · N arrays. Then, during the
second pass, the backward-horizontal and backward-
vertical passes are processed, and within the same
step the final aggregated cost (10) is also computed.
Then the best disparity is determined as in (9).
Overall,
computational cost is between 3 and 4 times that
of the standard local stereo algorithm. Memory re-
quirements are also small – O(2× M × N).
A PRACTICAL STEREO SYSTEM BASED ON REGULARIZATION AND TEXTURE PROJECTION
7
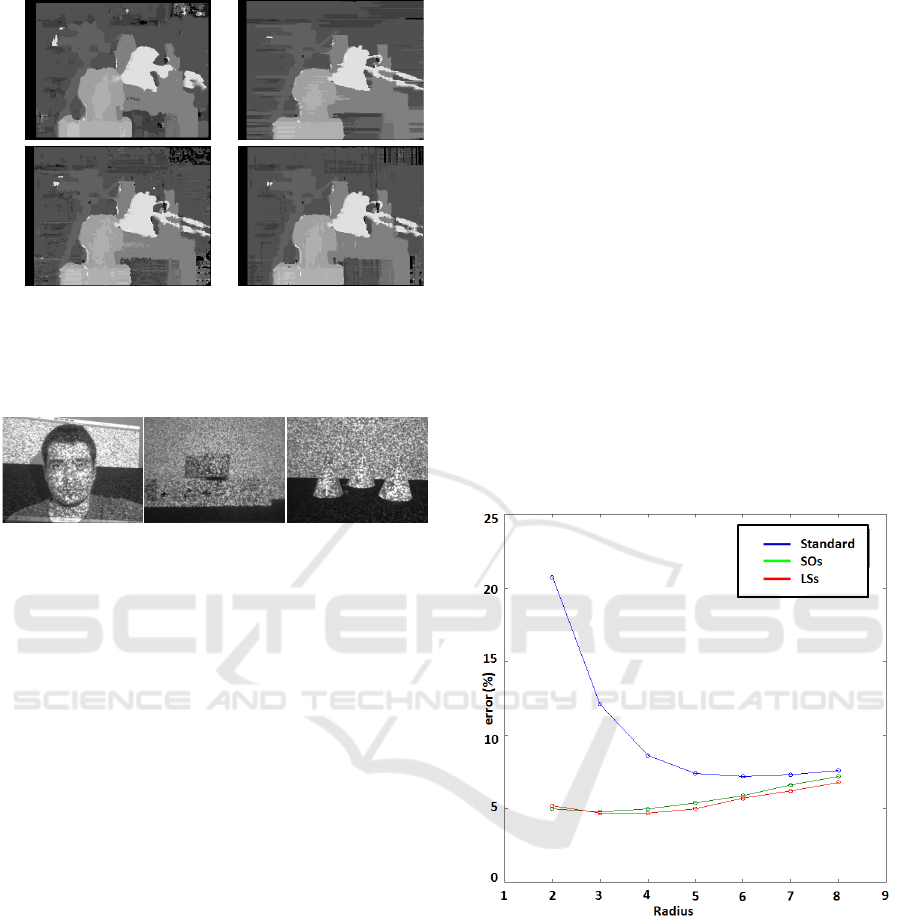
a)
b)
c)
d)
Figure 2: Qualitative comparison of different algorithms
based on the smoothness constraint: a)standard b)SO-based
c)local smoothness (2 horizontal scanlines) d)local smooth-
ness (4 scanlines).
Figure 3: Dataset used for experiments: from left to right,
Face, Cubes, Cones sequences.
2.3 Experimental Evaluation
In this section we briefly present some experimen-
tal results showing the capabilities of the previously
introduced regularization methods on stereo data by
comparing them to a standard block-correlation stereo
algorithm. In particular, in addition to the LS
s
algo-
rithm, we consider a particularly efficient approach
based only on one forward and one backward hori-
zontal SO pass (M. Bleyer, 2008). This algorithm ac-
counts for low memory requirements and fast perfor-
mance, though it tends to suffer the streaking effect.
We will refer to this algorithm as SO
s
.
Fig. 2 shows some qualitative results on the
Tsukuba dataset (Scharstein and Szeliski, 2002). The
standard local algorithm is in (a), SO
s
(b) and the LS
s
algorithm in (d). Also, the figure shows the disparity
map obtained by the use of the Local Smoothness cri-
terion over only 2 horizontal scanlines in (c). It can
be noticed that, compared to the standard approach,
regularization methods allow for improved accuracy
along depth borders. Furthermore, while methods
based only on horizontal scanlines (b, c) present typ-
ical horizontal streaking effects, these are less notice-
able in the LS
s
algorithm (d). In our implementation,
using standard incremental techniques but no SIMD
or multi-thread optimization, time requirements on a
standard PC for the standard, SO
s
and LS
s
algorithms
are 18, 62 and 65 ms, respectively.
In addition, we show some results concerning im-
ages where a pattern is projected on the scene. As for
the pattern, we use a randomly-generated grayscale
chessboard, which is projected using a standard video
projector. Fig. 3 shows 3 frames taken from 3 stereo
sequences used here and in Section 3.4 for our ex-
periments. Sequence Face is a static sequence, while
Cubes and Cones are dynamic scenes where the ob-
jects present in the scene rapidly shift towards one
side of the table. All frames of all sequences are
640× 480 in resolution.
Figure 4 shows experimental results for the stan-
dard algorithm as well as SO
s
and LS
s
over different
window sizes. Similarly to what done in (Davis et al.,
2005), ground truth for this data is the disparity map
obtained by the spacetime stereo technique (see next
Section) over all frames of the sequence using a 5× 5
window patch. A point in the disparity map is con-
sidered erroneous if the absolute difference between
it and the groundtruth is higher than one.
Figure 4: Quantitative comparison between different spatial
approaches: standard algorithm, SO
s
, LS
s
.
From the figure it is clear that, even on this real
dataset, regularization methods allow for improved
results compared to standard methods since the curve
concerningthe standard algorithm is always abovethe
other two. It is worth pointing out that both SO
s
and
LS
s
achievetheir minimum with a smaller spatial win-
dow compared to the standard algorithm, allowing for
reduced smearing effect along depth borders. Con-
versely, the use of regularization methods with big
windows increase the error rate which tends to con-
verge to the one yielded by the standard method. It is
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
8
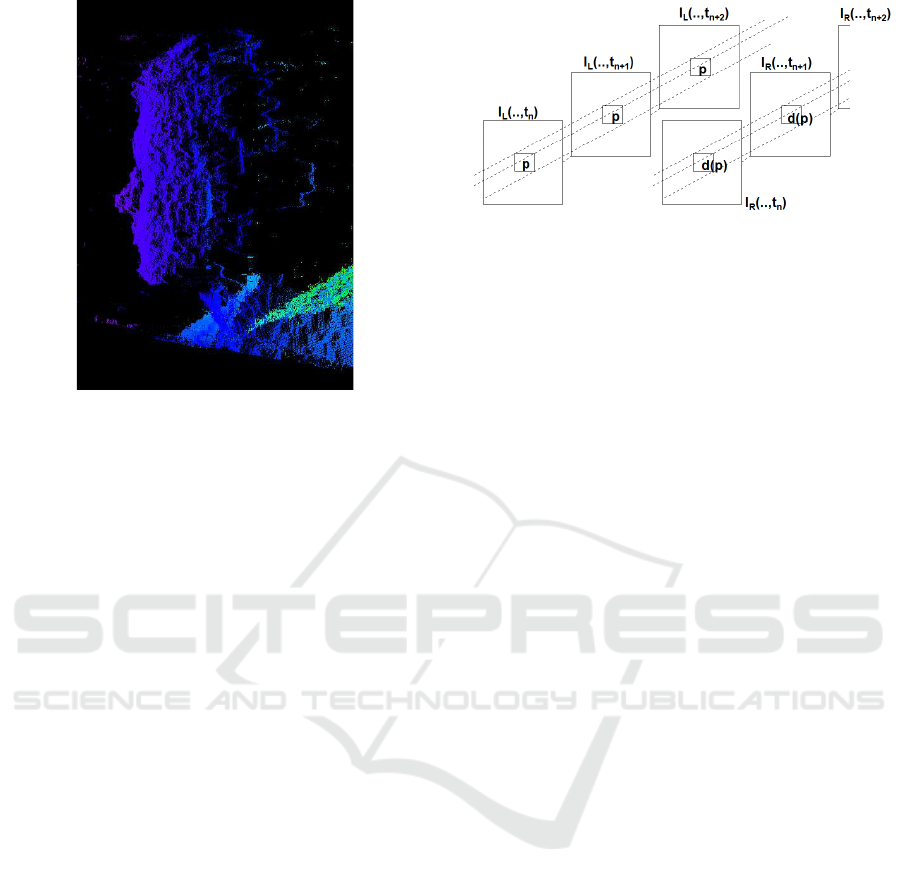
Figure 5: Point cloud showing the 3D profile of the face in
Fig. 3 (left), computed using a single frame and LS
s
algo-
rithm.
also worth pointing out that overall the best result is
yielded by the proposed LS
s
algorithm. Finally, Fig-
ure 5 shows the 3D point cloud of the face profile
obtained by using the LS
s
algorithm over one frame
on the Face dataset. From the Figure it can be noted
that despite being fast and memory-efficient, this al-
gorithm is able to obtain good accuracy in the recon-
structed point cloud.
3 SPACETIME STEREO
Block-correlation stereo uses a spatial window to
smooth out noise in stereo matching. A natural ex-
tension is to extend the window over time, that is, to
use a spatio-temporal window to aggregate informa-
tion at a pixel (Zhang et al., 2003), (Davis et al., 2005)
(Figure 6). The intensity at position I(p, t) is now de-
pendent on time, and the block-matching sum over a
set of frames F and a spatial windowW can be written
as
C(p, d) =
∑
t∈F
∑
q∈W(p)
e(I
L
(q,t), I
R
(δ(q),t)). (11)
Minimizing C over d yields an estimated disparity at
the pixel p. Note that we obtain added information
only if the scene illumination changes within F.
As pointed out in (Zhang et al., 2003), block
matching in Equation (11) assumes that the dispar-
ity d is constant over both the local neighborhood W
and the frames F. Assuming for the moment that the
scene is static, by using a large temporal window F
Figure 6: Spacetime window for block matching. Spatial
patches centered on p are matched against corresponding
patches centered on d(p), and the results summed over all
frames.
we can reduce the size of the windowW while still re-
ducing matching noise. This strategy has the further
salutary effect of minimizing the smearing of object
boundaries. Figure 1 (top) shows a typical result for
spacetime block matching of a static scene with small
spatial windows.
3.1 Moving Objects
In a scene with moving objects, the assumption of
constant d over F is violated. A simple scheme to
deal with motion is to trade off between spatial and
temporal window size (Davis et al., 2005). In this
method, a temporal window of the last k frames is
kept, and when a new frame is added, the oldest frame
is popped off the window, and C(p, d) is calculated
over the last k frames. We will refer to this approach
as sliding windows (STS-SW). The problem is that
any large image motion between frames will com-
pletely erase the effects of temporal integration, es-
pecially at object boundaries (see Figure 1, bottom-
left). It is also suboptimal, since some areas of the
image may be static, and would benefit from longer
temporal integration.
A more complex method is to assume locally lin-
ear changes in disparity over time, that is, d(p,t) is a
linear function of time (Zhang et al., 2003):
d(p,t) ≈ d(p,t
0
) + α(p)(t − t
0
). (12)
For smoothly-varying temporal motion at a pixel, the
linear assumption works well. Unfortunately, search-
ing over the space of parameters α(p) makes min-
imizing the block-match sum (11) computationally
difficult. Also, the linear assumption is violated at
the boundaries of moving objects, where there are
abrupt changes in disparity from one frame to the next
(see Figure 7). These temporal boundaries present the
same kind of challenges as spatial disparity bound-
aries in single-frame stereo.
A PRACTICAL STEREO SYSTEM BASED ON REGULARIZATION AND TEXTURE PROJECTION
9

Figure 7: Disparity at a single pixel during object mo-
tion. Initially disparity is constant (no motion); then varies
smoothly as the object moves past the pixel. At the object
boundary there is an abrupt change of disparity.
A more sophisticated strategy would be to detect
the temporal boundaries and apply temporal smooth-
ness only up to that point. In this way, static im-
age areas enjoy long temporal integration, while those
with motion use primarily spatial information. Hence,
we propose a novel method with the aim of ef-
ficiently dealing with dynamic scenes and rapidly-
varying temporal boundaries. In particular, the main
idea is to avoid using the spacetime stereo formula-
tion as in (11) which blindly averages all points of the
scene over time, instead enforcing a temporal smooth-
ness constraint similarly to what is done spatially.
In particular, this can be done either modelling the
spatio-temporal structure with a MRF and solving us-
ing an SO or DP-based approach, or enforcing a local
smoothness constraint as described in Section 2.
3.2 Temporal Regularization using SO
The idea of looking for temporal discontinuities was
first discussed in (Williams et al., 2005), which pro-
posed an MRF framework that extends over three
frames. The problem with this approach is that the
cost in storage and computation is prohibitive, even
for just 3 frames. Here we propose a much more effi-
cient method that consists in defining a scanline over
time, analogous to the SO method over space. Given
a cost array for each point and time instant C(p, d,t)
being computed by means of any spatial method (lo-
cal, global, DP-based, ··· ), a SO-based approach is
used for propagating forward a smoothness constraint
over time:
A
SO
(p, d,t) = C(p, d,t) + min
d
′
{A
SO
(p, d
′
,t − 1) + ρ(d,d
′
)}
(13)
Instead of backtracking the minimum cost path as in
the typical DP algorithm, here it is more convenient
to compute the best disparity over space and time as
follows:
d
∗
(p,t) = argmin
d
{A
SO
(p, d,t)} (14)
so that for each new frame its respective disparity im-
age can be readily computed. As shown in Figure
Figure 8: Local smoothing applied in the temporal domain.
Disparity values influence the center pixel at time t
n
from
vertical and horizontal directions, and also from previous
frames t
i
, i < n.
8, accumulated costs from previous frames t
i<n
are
propagated forward to influence the correlation sur-
face at time t
n
. Here we propose to use as spatial algo-
rithm the SO-based approach deploying two horizon-
tal scanlines as discussed in Section 2. This algorithm
is referred to as SO
s,t
.
3.3 Temporal Regularization using
Local Smoothness
In a manner similar to applying SO across frames, we
can instead use local smoothness. The key idea is to
modify the correlation surface at position p and time t
according to the best disparity found at the same point
p at the previous instant t − 1. This does not require
storing and propagating a cost array, only the corre-
spondences found at the previous time instant.
The local temporal smoothness criterion is orthog-
onal to the strategy adopted for solving stereo over the
spatial domain, hence any local or global stereo tech-
niques can be used together with it. Here we propose
to use local spatial smoothness described in Section
2. The cost function at pixel p and time t becomes:
A
LS
s,t
(p, d,t) = C(p, d,t) +
∑
q∈N
ρ(d, d(q,t)) + ρ(d, d(p,t − 1)), (15)
That is, the penalty terms added to the local cost are
those coming from the 4 independent scanline-based
processes at time t plus an additional one that depends
on the best disparity computed at position p at the
previous time instant (see Figure 8). This algorithm
will be referred to as LS
s,t
.
It is possible to propagate information both for-
wards and backwards in time, but there are several
reasons for only going forwards. First, it keeps the
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
10

Table 1: Percentage of errors, Cubes stereo sequence.
Radius STS-SW Standard SO
s
SO
s,t
LS
s
LSs, t
2 12.8 12.1 1.1 1.0 1.1 0.7
Table 2: Percentage of errors, Cones stereo sequence.
Radius STS-SW Standard SO
s
SO
s,t
LS
s
LSs, t
1 46.9 49.9 5.3 5.2 14.8 12.2
3 35.4 15.9 4.2 4.1 8.2 6.9
5 31.9 9.6 4.6 4.5 7.0 6.1
Figure 9: Comparison of error percentages between differ-
ent approaches for the Cubes sequence at each frame of the
sequence. [The graph uses two different scales for better
visualization].
data current – previous frames may not be useful for a
realtime system. Second, the amount of computation
and storage is minimal for forward propagation. Only
the previous image local costs have to be maintained,
which is O(M · N). In contrast, to do both forwards
and backwards smoothing we would need to save lo-
cal costs over k frames (O(k · M · N)), and worse, re-
compute everything for the previous k frames, where
k is the size of the temporal window for accumulation.
3.4 Experiments
This section presents experimental results over two
stereo sequences with moving objects and a projected
pattern, referred to as Cubes and Cones (see Fig. 3).
To obtain ground truth for the stereo data, each differ-
ent position of the objects is captured over 30 frames
with a 3× 3 spatial window, and stereo depths are av-
eraged over time by means of spacetime stereo. Then,
a sequence is built up by using only one frame for
each different position of the objects.
As a comparison, we compute spacetime stereo
using the sliding window approach (STS-SW). This
approach is compared with regularization techniques
based only on spatial smoothness (i.e. SO
s
, LS
s
) as
well as with those enforcing temporal regularization
(i.e. SO
s,t
, LS
s,t
).
Figure 9 shows the error rates of each algorithm
for each frame of the Cubes dataset, with a fixed spa-
tial window of radius 2. Table 1 reports the average
error over the whole sequence. In addition, Figure 1
shows the ground truth for one frame of the sequence
as well as the results obtained by STS− SW and LS
s,t
.
As can be seen, due to the rapid shift of the objects in
the scene, the approach based on spacetime stereo is
unable to improve the results compared to the stan-
dard algorithm. Instead, approaches based on spa-
tial regularization yield very low error rates, close to
those obtained by the use of spacetime stereo over the
same scene but with no moving objects. Furthermore,
Figure 9 shows that the error variance of the methods
enforcing the smoothness constraint is notably lower
than that reported by the standard and STS-SW algo-
rithms. It is worth pointing out that the use of the
proposed LS regularization technique both in space
and time yields the best results over all the considered
frames.
As in the previous experiment, Table 2 shows the
mean error percentages over the Cones dataset with
different spatial windows (i.e., radius 1, 3, and 5).
Also in this case, regularization approaches achieve
notably lower error rates compared to standard and
spacetime approaches. From both experiments it is
possible to observe that the introduction of temporal
smoothness always helps improving the performance
of the considered regularization methods.
A PRACTICAL STEREO SYSTEM BASED ON REGULARIZATION AND TEXTURE PROJECTION
11

4 CONCLUSIONS AND FUTURE
WORK
In this paper we investigated the capabilities of a
3D sensor comprised of a stereo camera and a tex-
ture projector. With off-the-shelf hardware and un-
der real illumination conditions, we have shown that
in the presence of moving objects single-frame stereo
with regularization produces much better results than
STS. Moreover, the proposed regularization approach
based on local smoothness, though not based on a
global optimization, shows good performance and
reduced computational requirements. Finally, we
have found that the proposed introduction of tempo-
ral smoothness helps improving the performance of
the considered regularization methods.
We are currently actively developing a small, low-
power stereo device with texture projection. There
are two tasks that need to be accomplished. First,
we are trying to optimize the local smoothness con-
straint to be real time on standard hardware, that is,
to run at about 30 Hz on 640x480 images. Second,
we are designing a small, fixed pattern projector that
will replace the video projector. The challenge here
is to project enough light while staying eye-safe and
having a compact form factor. Using the methods de-
veloped in this paper, we believe we can make a truly
competent realtime 3D device for near-field applica-
tions.
The code concerning the regularization methods
and the STS algorithms used in this paper is open
source and available online
1
.
REFERENCES
Anderson, D., Herman, H., and Kelly, A. (2005). Experi-
mental characterization of commercial flash ladar de-
vices. In Int. Conf. of Sensing and Technology.
Curless, B. and Levoy, M. (1995). Better optical triangula-
tion through spacetime analysis. In ICCV.
Davis, J., Nehab, D., Ramamoorthi, R., and Rusinkiewicz,
S. (2005). Spacetime stereo: a unifying framework
dor depth from triangulation. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 27(2).
Felzenszwalb, P. and Huttenlocher, D. (2004). Efficient be-
lief propagation for early vision. In Proc. CVPR, vol-
ume 1, pages 261–268.
Gong, M. and Yang, Y. (2005). Near real-time reliable
stereo matching using programmable graphics hard-
ware. In Proc. CVPR, volume 1, pages 924–931.
Hirschmuller, H. (2005). Accurate and efficient stereo pro-
cessing by semi-global matching and mutual informa-
tion. In Proc. CVPR, volume 2, pages 807–814.
1
prdev.willowgarage.com/trac/personalrobots/browser/pkg/trunk/vision/
Kim, J., Lee, K., Choi, B., and Lee, S. (2005). A dense
stereo matching using two-pass dynamic program-
ming with generalized ground control points. In Proc.
CVPR, pages 1075–1082.
Klaus, A., Sormann, M., and Karner, K. (2006). Segment-
based stereo matching using belief propagation and a
self-adapting dissimilarity measure. In Proc. ICPR,
volume 3, pages 15–18.
Kolmogorov, V. and Zabih, R. (2001). Computing visual
correspondence with occlusions via graph cuts. In
Proc. ICCV, volume 2, pages 508–515.
Konolige, K. (1997). Small vision systems: hardware and
implementation. In Eighth International Symposium
on Robotics Research, pages 111–116.
M. Bleyer, M, G. (2008). Simple but effective tree struc-
tures for dynamic programming-based stereo match-
ing. In Proc. Int. Conf. on Computer Vision Theory
and Applications (VISAPP), volume 2.
Nishihara, H. K. (1984). Prism: A practical real-time imag-
ing stereo matcher. Technical report, Cambridge, MA,
USA.
Potts, R. (1995). Some generalized order-disorder transi-
tions. In Proc. Cambridge Philosophical Society, vol-
ume 48, pages 106–109.
Salvi, J., Pages, J., and Batlle, J. (2004). Pattern docifi-
cation strategies in structured light systems. Pattern
Recognition, 37(4).
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. Int. J. Computer Vision, 47(1/2/3):7–42.
Williams, O., Isard, M., and MacCormick, J. (2005). Es-
timating disparity and occlusions in stereo video se-
quences. In Proc. CVPR.
Yang, Q., Wang, L., Yang, R., Wang, S., Liao, M., and Nis-
ter, D. (2006). Real-time global stereo matching using
hierarchical belief propagation. In Proc. British Ma-
chine Vision Conference.
Yang, Q. e. a. (2006). Stereo matching with color-weighted
correlation, hierachical belief propagation and occlu-
sion handling. In Proc. CVPR, volume 2, pages 2347
– 2354.
Zhang, L., Curless, B., and Seitz, S. (2003). Spacetime
stereo: shape recovery for dynamic scenes. In Proc.
CVPR.
Zhao, J. and Katupitiya, J. (2006). A fast stereo vision al-
gorithm with improved performance at object borders.
In Proc. Int. Conf. on Intelligent Robots and Systems
(IROS), pages 5209–5214.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
12
