
INDUCED ℓ
∞
− OPTIMAL GAIN-SCHEDULED FILTERING OF
T
AKAGI-SUGENO FUZZY SYSTEMS
Isaac Yaesh
Control Department, IMI Advanced Systems Div., P.O.B. 1044/77, Ramat–Hasharon, 47100, Israel
Uri Shaked
School of Electrical Engineering, Tel Aviv University, Tel Aviv, 69978, Israel
Keywords:
Takagi-Sugeno fuzzy systems, Polytopic uncertainties, H
∞
-optimization, ℓ
∞
-optimization, S -procedure, Lin-
ear matrix inequalities.
Abstract:
The problem of designing gain-scheduled filters with guaranteed induced ℓ
∞
norm for the estimation of the
state-vector of finite dimensional discrete-time parameter-dependent Takagi-Sugeno Fuzzy Systems systems
is considered. The design process applies a lemma which was recently derived by the authors of this paper,
characterizing the induced ℓ
∞
norm by Linear Matrix Inequalities. The suggested filter has been successfully
applied to a guidance motivated estimation problem, where it has been compared to an Extended Kalman
Filter.
1 INTRODUCTION
The theory of optimal design of estimators for linear
discrete-time systems in a state-space formulation has
been first established in (Kalman, 1960). The original
problem formulation assumed Gaussian white noise
models for both the measurement noise and the ex-
ogenous driving process. For this case, the results
of (Kalman, 1960) provided the Minimum-Mean-
Square Estimator (MMSE). The Kalman filter has
found since then many applications (see e.g. (Soren-
son, 1985) and the references therein). Following the
introduction of H
∞
control theory in (Zames, 1981),
a method for designing discrete-time H
∞
optimal es-
timators within a deterministic framework has been
developedin (Yaesh and Shaked, 1991), where the ex-
ogenous signals are of finite energy. The case where
the driving signal is of finite energy (e.g. piecewise
constant for a finite time) ,whereas the measurement
noise is white has been recently considered in (Yaesh
and Shaked, 2006). However, in some cases the min-
imization of the maximum absolute value of the es-
timation error (namely the ℓ
∞
−norm) rather than the
error energy is required where the exogenous signals
are also of finite ℓ
∞
−norm. In such cases, an induced
ℓ
∞
−norm is obtained which is often referred to as an
ℓ
1
problem due to the fact that the induced-ℓ
∞
−norm
for a linear system is just the ℓ
1
-norm of its impulse
response and an upper-bound on the ℓ
1
-norm of its
transfer function (see (Dahleh and Pearson, 1987)).
In the present paper, the problem of discrete-
time optimal state-estimation in the minimum in-
duced ℓ
∞
−norm sense is considered for a class of
Takagi-Sugeno fuzzy systems. The plant model for
the systems considered, is described by a collection
of ’sample’ finite-dimensional linear-time-invariant
plants which possess the same structure but differ
in their parameters. All possible plant models are
then assumed to be convex combinations of these spe-
cific plant models (namely a polytopic system where
the ’sample’ plant models are denoted as its vertices
(Boyd et al., 1994)). The solution of the estima-
tion problem is characterized by LMIs (Linear Ma-
trix Inequalities) based on the quadratic stability as-
sumption. We note that more recent developments of
(Geromel et al., 2000) include gain scheduled filter
synthesis for the cases of linear (Tuan et al., 2001)
and nonlinear (Hoang et al., 2003) dependence on the
parameterswith parameter dependentLyapunovfunc-
tions. We also note that in (Salcedo and Martinez,
2008) related results appear where the continuous-
time fuzzy output feedback and filtering were con-
sidered in parallel to the discrete-time results of the
present paper.
The paper is organized as follows. In Section 2,
the problem is formulated and a key lemma character-
67
Yaesh I. and Shaked U.
INDUCED â
ˇ
D ¸Sâ
´
L
¯
d â
´
LŠ OPTIMAL GAIN-SCHEDULED FILTERING OF TAKAGI-SUGENO FUZZY SYSTEMS.
DOI: 10.5220/0002169500670073
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page
ISBN: 978-989-674-001-6
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

izing the induced ℓ
∞
−norm in terms of LMIs is pre-
sented. In Section 3 the filter design inequalities are
obtained. Section 4 considers a numerical example
dealing with a robust gain scheduled tracking prob-
lem. Finally, Section 5 brings some concluding re-
marks.
Notation: Throughout the note the superscript
‘T’ stands for matrix transposition, R
n
denotes the
n dimensional Euclidean space, R
n×m
is the set of
all n ×m real matrices, and the notation P > 0, for
P ∈R
n×n
means that P is symmetric and positive def-
inite. The space of square summable functions over
[0 ∞] is denoted by l
2
[0 ∞], and ||.||
2
stands for the
standard l
2
-norm,||u||
2
= (Σ
∞
k=0
u
T
k
u
k
)
1/2
. We also use
||.||
∞
for the l
∞
-norm namely, ||u||
2
∞
= sup
k
(u
T
k
u
k
).
The convex hull of a and b is denoted by C o{a, b},
I
n
is the unit matrix of order n, and 0
n,m
is the n ×m
zero matrix and I
m,n
is a version of I
n
with last n−m
rows omitted.
2 PROBLEM FORMULATION
AND PRELIMINARIES
We consider the following linear system:
x(k+ 1) = A(k)x(k) + Bw(k), x(0) = x
0
y(k) = C(k)x(k) + Dw(k)
z(k) = L(k)x(k)
(1)
where x ∈ R
n
is the system states, y ∈R
r
is the mea-
surement, w ∈ R
q
includes the driving process and
the measurement noise signals and it is assumed to
have bounded ℓ
∞
−norm. The sequence z ∈ R
m
is the
state combination to be estimated and A, B, C, D and
L are matrices of the appropriate dimensions.
We assume that the system parameters lie within
the following polytope
Ω :=
A B C D L
(2)
which is described by its vertices. That is, for
Ω
i
:=
A
i
B
i
C
i
D
i
L
i
(3)
we have
Ω = C o{Ω
1
,Ω
2
,...,Ω
N
} (4)
where N is the number of vertices. In other words:
Ω =
N
∑
i=1
Ω
i
f
i
,
N
∑
i=1
f
i
= 1 , f
i
≥ 0. (
5)
Assuming that f
i
are exactly known, the above sys-
tem is just a Tagaki-Sugeno fuzzy system. To see this,
one may introduce new parameters s
i
(t),i = 1, 2,..., p
(so called premise variables, see (Tanaka and Wang,
2001)) possibly depending on the state-vector x(t),
external disturbances and/or time (Tanaka and Wang,
2001) and rewrite (1) as :
IF s
1
is M
i1
and s
2
is M
i2
and ... s
p
is M
ip
THEN
x(k+ 1) = A
i
(k)x(k) + B
i
w(k), x(0) = x
0
y(k) = C
i
(k)x(k) + D
i
w(k)
z(k) = L
i
(k)x(k)
i = 1, 2,..., N
(6)
where M
ij
is the fuzzy set and N is the
number of model rules. Defining s(t) =
col{s
1
(t),s
2
(t),...,s
p
(t)},
ω
i
(s(t)) = Π
p
j= 1
M
ij
(s
j
(t))
and
f
i
(s(t)) =
ω
i
(t)
Σ
N
i=1
ω
i
(s(t))
we readily get the representation of (1). We, there-
fore, assume indeed that the p premise scalar vari-
ables s
i
(t),i = 1,2,..., p, and, consequently f
i
are ex-
actly known and consider the following filter:
ˆx(k+ 1) = Aˆx(k) + K(k)(y−Cˆx), ˆz(k) = Lˆx(k)
(7)
where the filter gain is given by the following:
K =
N
∑
i=1
K
i
f
i
(8)
and where A =
N
∑
i=1
A
i
f
i
and L =
N
∑
i=1
L
i
f
i
. We will dif-
ferently treat, in the sequel, the case where C is con-
stant and the case where C =
N
∑
i=1
C
i
f
i
.
Our aim is to find the filter parameters K
i
so that
the following induced ℓ
∞
−norm condition is satisfied.
sup
w∈ℓ
∞
||z− ˆz||
∞
/||w||
∞
< γ (9)
To solve this problem we will first define another
polytopic system :
¯
Ω :=
¯
A
¯
B
¯
C
¯
D
(10)
which is described by the vertices:
¯
Ω
i
:=
¯
A
i
¯
B
i
¯
C
i
¯
D
i
, i = 1,...,N (11)
The system of (10)-(11) will represent, in the sequel,
the dynamics of the estimation error for the system
(1). The following technical lemma will be needed
in order to provide convex characterization of the in-
duced ℓ
∞
− norm of the estimation error system:
Lemma 1. The system
¯x(k+ 1) =
¯
A(k) ¯x(k) +
¯
Bw(k), x(0) = x
0
z(k) =
¯
C(k) ¯x(k) +
¯
D ¯w(k)
(12)
satisfies
sup
w∈ℓ
∞
||z||
∞
/||w||
∞
< γ (13)
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
68

if the following matrix inequalities are satisfied for
i = 1,2,
...,N:
¯
A
T
i
P
¯
A
i
+ λP−P
¯
A
T
i
P
¯
B
i
¯
B
T
i
P
¯
A
i
−µI +
¯
B
T
i
P
¯
B
i
< 0 (14)
and
λP 0
¯
C
T
i
0 (γ−µ)I
¯
D
T
i
¯
C
i
¯
D
i
γI
> 0 (15)
so that P > 0, µ > 0 and λ < 1.
The proof of this lemma is given in (Shaked and
Yaesh, 2007) and is also provided, for the sake of
completeness, in Appendix A.
Remark. Note that (14) can be written, using
Schur complements ((Boyd et al., 1994)), as follows:
P−λP 0
¯
A
T
i
P
0 µI
¯
B
T
i
P
P
¯
A
i
P
¯
B
i
P
> 0 (16)
or equivalently as
P−λP 0
¯
A
T
i
0 µI
¯
B
T
i
¯
A
i
¯
B
i
P
−1
> 0 (17)
The fact that the inequality (16) is affine in
¯
A
i
and
¯
B
i
will be utilized in the sequel to obtain convex charac-
terization (i.e. in LMI form) of the filter parameters
K
i
.
3 GAIN SCHEDULED FILTERING
Defining the state estimation error to be:
e(k) = x(k) − ˆx(k) (18)
we readily have for the case where f
i
are available for
the estimation process, that
e(k+ 1) = (A−K(k)C)e(k) + (B−K(k)D)w(k)
(19)
and
z(k) − ˆz(k) = Le(k) (20)
We substitute
¯
A
i
= A
i
−K
i
C,
¯
B
i
= B
i
−K
i
D and
¯
C = L
i
in (14) and (15) where we restrict our attention
to the case where C and D are not vertex dependent
(i.e. C
i
= C,D
i
= D,i = 1,2, ...,N). In this case, we
define Y
i
= PK
i
and readily obtain from (16) and (15)
that
P−λP 0 A
T
i
P−C
T
Y
T
i
0 µI B
T
i
P−D
T
Y
T
i
PA
i
−Y
i
C PB
i
−Y
i
D P
> 0
(21)
and
λP 0 L
T
i
0 (γ−µ)I 0
L
i
0 γI
> 0, λ < 1 (22)
We, therefore, obtain the following result:
Theorem 1. Consider the estimator of (12) for the
system of (1) with C
i
= C, D
i
= D,i = 1, 2,..., N. The
estimation error satisfies (9) if (21) and (22) are satis-
fied for i = 1, 2,..., N so that P > 0, µ > 0 and λ < 1.
We next address the problem where C and D are
vertex dependent. To this end we consider a version
of Lemma 1 which can be written in terms of Ω rather
than Ω
i
, namely we replace (16) and (14) by:
P−λP 0
¯
A
T
P
0 µI
¯
B
T
P
P
¯
A P
¯
B P
> 0 (23)
and
λP 0
¯
C
T
0 (γ−µ)I
¯
D
T
¯
C
¯
D γI
> 0 (24)
and substitute
¯
A =
∑
N
i, j=1
(A
i
− K
i
C
j
) f
i
f
j
,
¯
B
i
=
∑
N
i, j=1
(B
i
−K
i
D
j
) f
i
f
j
and
¯
C =
∑
N
i=1
L
i
f
i
. We obtain
defining Y
i
= PK
i
:
N
∑
i, j=1
G
ij
f
i
f
j
> 0 (
25)
where
G
ij
:=
P−λP 0 A
T
i
P−C
T
j
Y
T
i
0 µI B
T
i
P−D
T
j
Y
T
i
PA
i
−Y
i
C
j
PB
i
−Y
i
D
j
P
(26)
and
N
∑
i=1
λP 0 L
T
i
0 (γ−µ)I 0
L
i
0 γI
f
i
> 0 (
27)
Since, however (see (Tanaka and Wang, 2001))
equation (25) can be also written as
N
∑
i, j=1
G
ij
f
i
f
j
=
N
∑
i=1
G
ii
f
2
i
+ 2
N
∑
i=1
∑
i< j
G
ij
+ G
ji
2
f
i
f
j
(
28)
Defining a simple transformation of the convex co-
ordinates f
k
so that for k = 1,2,...,N we set h
k
= f
2
k
where as the remaining h
k
for k = N+1,N+2,...,N+
N(N−1)
2
a
re defined by h
k
= 2f
i
f
j
, j = 1,2...,N,i < j.
Since obviously
∑
N+
N(N−1)
2
k=1
h
k
= 1
where h
k
≥ 0 they
can serve as convex coordinates. We, therefore, define
the following LMIs inspired by (Tanaka and Wang,
2001),
G
ii
> 0,i = 1, 2,...N and G
ij
+ G
ji
> 0,i < j (29)
INDUCED - OPTIMAL GAIN-SCHEDULED FILTERING OF TAKAGI-SUGENO FUZZY SYSTEMS
69

and obtain the following result:
Theorem 2. Consider the estimator (12) for the
system (1). The estimation error satisfies (9) if (29)
and (22) for i = 1,2,...,N are satisfied so that P > 0,
µ > 0 and λ < 1.
The solution offered above, for the case where C
and D are uncertain and are known to reside in a given
polytope, seeks a single matrix P that solves the LMIs
for
N(N+1)
2
vertices, instead of the N vertices that were
solved for in the case of known C and D. A solu-
tion for such large number of vertices by a single P
entails a significant overdesign. Even the relaxation
offered by e.g. (Shaked, 2003) to reduce the overde-
sign by allowing different P
i
,i = 1,2,...,
N(N+1)
2
for
the
N(N+1)
2
vertices still suffers from a considerable
conservatism. Moreover, the computational complex-
ity of the solution also rapidly increases as a function
of the number of vertices.
In many cases,C resides in some uncertainty poly-
tope, while D is fixed and known. In such a case, an
alternative way to deal with the problem is to define
ξ(k) = col{x(k), y(k)} and ˜w(k) = col{w(k), w(k +
1)}so that the augmented system becomes:
ξ(k+ 1) =
˜
A(k)x(k) +
˜
B ˜w(k)
y(k) =
˜
C(k)ξ(k) +
˜
D ˜w(k)
z(k) =
˜
L(k)ξ(k)
where
˜
A=
A 0
CA 0
˜
B=
B 0
CB D
,
˜
C=
0 I
r
,
˜
L=
L 0
, and
˜
D =
D 0
(30)
In (30) the uncertainties appear in
¯
A and
¯
B only and,
therefore, Theorem 1 above may be invoked. We,
therefore, obtain the following result which offers
reduced conservatism with respect the correspond-
ing continuous-time results of (Salcedo and Martinez,
2008):
Theorem 3. Consider the estimator of (12) for the
system of (1) for D
i
= D, i = 1,2,...,N. The estima-
tion error satisfies (9) with γ replaced by
√
2γ if (21)
and (22) are satisfied for i = 1,2, ...,N so that P > 0,
µ > 0 and λ < 1 with A,B,C,L replaced by
˜
A,
˜
B,
˜
C,
˜
L
of (30).
4 EXAMPLE
We consider the dynamic model of guidance in a
plane:
˙
˜x = νcos(
˜
ψ) + w
1
˙
˜y = νsin(
˜
ψ) + w
2
˙
˜
ψ =
˜
φ
˙
φ = −φ/τ+ u/τ
(31)
where ˜x and ˜y are the first two coordinates of a flight
vehicle cruising in a constant altitude, in a local level
north-east-down system,
˜
ψ is the vehicle body an-
gle with respect to the north (i.e. azimuth angle)
and φ is the vehicle’s roll angle assumed to be gov-
erned by a first-order low-pass filter dynamics hav-
ing a time-constant of τ seconds, driven by the roll-
angle command u. The wind velocities at the north
and east directions respectively are denoted by w
1
and
w
2
whereas ν is the true-air-speed. Our aim is to filter
the noisy measurements of ˜x, ˜y and φ and to estimate
˜
ψ. Defining,
x = col{˜x, ˜y,vsin(
˜
ψ),vcos(
˜
ψ),φ}
the measurements vector which consists of noisy
measurements of the position components ˜x and ˜y and
the roll angle φ is given by
y = Cx+ R
1/2
v
where v is the measurement noise which is taken in
the simulations in the sequel as a 3-vector of zero-
mean unity variance white noise sequences but for all
practical purposes is assumed to be v ∈ ℓ
∞
. The noise
level is set by
R = diag{25, 25,0.1}
and the measurement matrix is
C =
1 0 0 0 0
0 1 0 0 0
0 0 0 0 1
Note that
˙x
1
= x
4
˙x
2
= x
3
˙x
3
= x
4
x
5
˙x
4
= −x
3
x
5
˙x
5
= −x
5
/τ+ u/τ
(32)
namely we have a bilinear system rather than a lin-
ear one. Following (Tanaka and Wang, 2001) with
a series of simple manipulations, this system can be
represented as a Takagi-Sugeno fuzzy system, namely
as a convex combination of linear systems where the
convex coordinates are online measured. To achieve
such a representation we recall that x
5
= φ is mea-
sured on line, and define s
1
= x
5
while neglecting
the small enough noise in measuring φ. The valid-
ity of the latter assumption will be verified in the se-
quel by the estimation quality we will obtain. Assum-
ing x
5
∈ [−φ
max
,φ
max
] we define f
1
=
s
1
−s
1,min
s
1,max
−s
1,min
=
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
70

x
5
+φ
m
ax
2φ
m
ax
, f
2
= 1− f
1
, α
1
= φ
max
and α
2
= −φ
max
. We
readily see that s
1
= φ
max
f
1
−φ
max
f
2
:= α
1
f
1
+ α
2
f
2
.
We note then that the system is then governed by
˙
ξ = A
c
(ξ)ξ+ B
c
w where ξ = col{x
1
,x
2
,x
3
,x
4
,x
5
}and
A
c
=
0 0 0 1 0
0 0 1 0 0
0 0 0 s
1
0
0 0 −s
1
0 0
0 0 0 0 −1/τ
Therefore, A
c
= A
c,1
α
1
+ A
c,2
α
2
where A
c,1
is ob-
tained from A
c
by replacing s
1
by α
1
and A
c,2
is sim-
ilarly obtained from A
c
by replacing s
1
by α
2
. We
also define w = col{w
1
,w
2
,ν
1
,ν
2
,ν
3
} and complete
the remaining matrices needed for the representation
of our problem (1)-(3) by applying a zero-order-hold
discrete-time equivalent of our continuous-time sys-
tem, where we have chosen a sampling time of h =
0.02. Due to the small enough h we have chosen, we
have e
Ah
= I + Ah+ O(h
2
) and we, therefore, readily
obtain that the system is governed by (1) and (3)-(5)
where A = A
1
α
1
+ A
2
α
2
+ O(h
2
) where
A
1
=
1.0000 −0.0002 0.0200 0
0 1.0000 0.0200 0.0002 0
0 0 0.9998 0.0209 0
0 0 −0.0209 0.9998 0
0 0 0 0 0.9231
A
2
=
1.0000 0 0.0002 0.0200 0
0 1.0000 0.0200 −0.0002 0
0 0 0.9998 −0.0209 0
0 0 0.0209 0.9998 0
0 0 0 0 0.9231
B
1
= B
2
= B =
0.2000 0 0 0 0
0 0.2000 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
and
D
1
= D
2
= D =
0 0 2.2361 0 0
0 0 0 2.2361 0
0 0 0 0 0.1000
We note at his point that, in order to mini-
mize the design conservatism stemming from the
quadratic stability assumption, we applied a pa-
rameter dependent Lyapunov function (Boyd et al.,
1994), max(x
T
P
1
x,x
T
P
2
x). Minimization of γ sub-
ject the the LMis that are obtained with this func-
tion to replace (21) and (22) (see Appendix B), us-
ing fminsearch.m from the optimization toolbox of
MATLAB
TM
and (Lagarias et al., 1998) to search
λ
i
, i = 1,2,3,4, ρ
1
, ρ2
2
, θ
1
and θ
2
, has resulted in
γ = γ
0
= 10.2732 and λ = 2.41×10
−7
. The follow-
ing gain matrices K
1
and K
2
have been obtained for
γ = γ
0
were obtained:
K
1
=
0.7574 −0.0007 0.0000
−0.0018 0.7593 0.0000
0.0000 0.0000 0.0000
0.0000 −0.0000 0.0000
−0.0000 −0.0000 0.0003
K
2
=
0.7558 −0.0024 0.0000
−0.0021 0.7613 −0.0000
−0.0000 0.0000 −0.0000
0.0000 0.0000 0.0000
−0.0000 0.0000 0.0003
This ℓ
∞
filter will be compared to an Extended
Kalman Filter (EKF, see (Jazwinsky, 1970)) based on
the nonlinear model of (31). Note that higher com-
plexity filters such as the particle filter (e.g. (Osh-
man and Carmi, 2006) are out the scope of the
present paper. For the simulations we take ν =
100m/s and try to control the vehicle to follow a
constant command at y = 5m, in spite of a wind
step at w
2
of 10m/s. The estimation results are
used to control the vehicle, using the simple law
u = −
0.0200 4.0000
ˆy−5
ˆ
ψ
T
where all
components of the initial state-vector are taken as
zero, besides y
0
= 20m. The EKF and the ℓ
∞
esti-
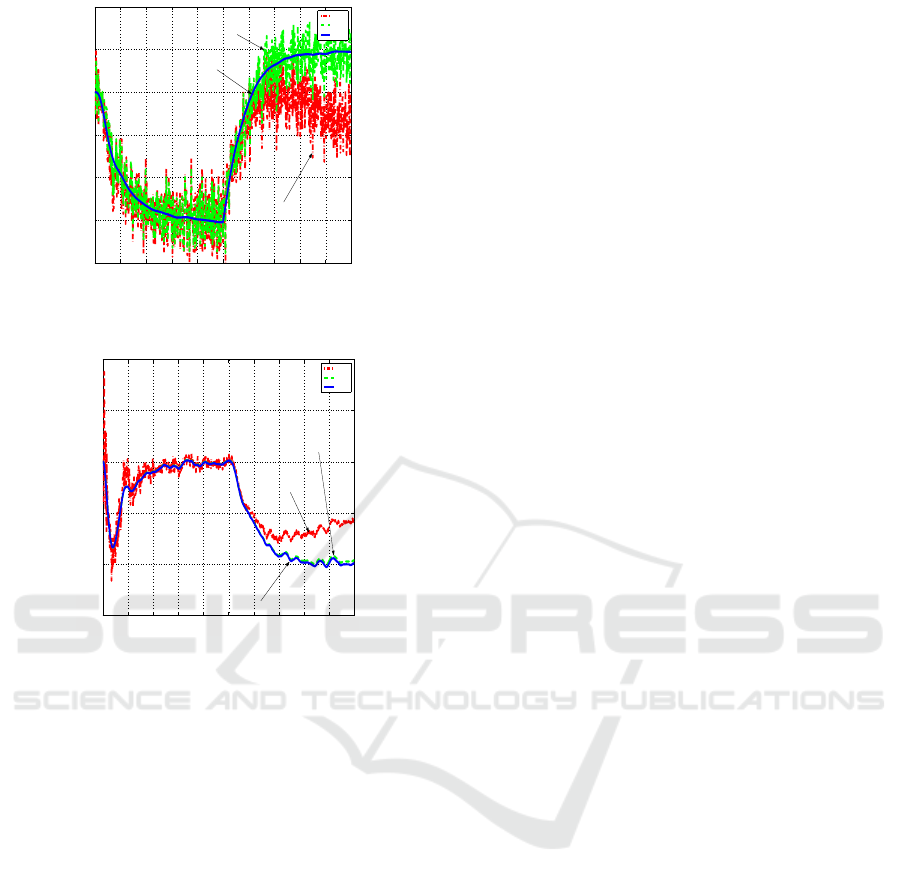
mated ˜x− ˜y trajectory results are compared in Fig. 1
to the true trajectory. One can notice the bias in the
EKF estimate. In Fig. 2, the true
˜
ψ and the estimated
values for
˜
ψ that are obtained by using the EKF and
the ℓ
∞
filter are depicted. We clearly see in this figure
that the ℓ
∞
filter outperforms the EKF which assumes
a white noise w
2
but leads to a bias when w
2
has a
bias. In contrast, the
˜
ψ estimate of the ℓ
∞
filter is
barely separable from the true values. Moreover, the
ℓ
∞
filter does not require the on-line numerical solu-
tion of a Riccati equation of order 4 and the gains are
obtained there by a simple convex interpolation on K
1
and K
2
. The fact that K
1
and K
2
are close to each
other is somewhat surprising. Our experience shows
that for a larger γ (i.e. suboptimal values), a larger
||K
1
−K
2
|| is obtained.
5 CONCLUSIONS
The problem of designing robust gain-scheduled fil-
ters with guaranteed induced ℓ
∞
−norm has been con-
sidered. The solution has been derived using a re-
cently developed bounded-real-lemma like condition
for bounding the induced ℓ
∞
norm of a system. This
result has been applied to derive the robust induced
ℓ
∞
−filter (or equivalently robust ℓ
1
filter) in terms of
LMIs. These LMIs have been applied to a guidance
motivated estimation example. In this example, the
INDUCED - OPTIMAL GAIN-SCHEDULED FILTERING OF TAKAGI-SUGENO FUZZY SYSTEMS
71
0 200 400 600 800 1000 1200 1400 1600 1800 2000
0
5
10
15
20
25
30
x [m]
y [m]
EKF
L
∞
True
L
∞
True
EKF
Figure 1: True, Extended Kalman Filter and ℓ
∞
-Filter Esti-
mated Trajectories - ˜x(t) versus ˜y(t).
0 2 4 6 8 10 12 14 16 18 20
−0.15
−0.1
−0.05
0
0.05
0.1
Time [sec]
ψ
EKF
L
∞
True
EKF
L
∞
True
Figure 2: True, Extended Kalman Filter and ℓ
∞
-Filter Esti-
mated Azimuth Angle -
˜
ψ versus t.
superiority of the induced ℓ
∞
filter over the Extended
Kalman Filter has been demonstrated, both in terms
of performance and simplicity of implementation.
REFERENCES
Abedor, J., Nagpal, K., and Poolla, K. (1996). A linear
matrix inequality approach to peak-to-peak gain min-
imization. International J. of Robust and Nonlinear
Control, 6:899–927.
Boyd, S., El-Ghaoui, L., Feron, L., and Balakrishnan, V.
(1994). Linear matrix inequalities in system and con-
trol theory. SIAM.
Dahleh, M. A. and Pearson, J. (1987). ℓ
1
-optimal feedback
controllers for mimo discrete-time systems. IEEE
Trans. on Automat. Contr., AC-32:314–322.
Geromel, J., Bernussou, J., Garcia, G., and de Oliviera, M.
(2000). h
2
and h
∞
robust filtering for discrete-time
linear systems. SIAM Journal of Control and Opti-
mization, 38:1353–1368.
Hoang, N., Tuan, H., Apkarian, P., and Hosoe, S. (2003).
Robust filtering for uncertain nonlinearly parame-
terized plants. IEEE Trans. on Signal Processing,
51:1806–1815.
Jazwinsky, A. H. (1970). Stochastic Processes and Filtering
Theory. Academic Press, New-York.
Kalman, R. (1960). A new approach to linear filtering and
prediction problems. Transactions ASME, Journal of
Basic Engineering, 82d:35–45.
Lagarias, J., Reeds, J. A., Wright, M. H., and Wright, P. E.
(1998). Convergence properties of the nelder-mead
simplex method in low dimensions. SIAM Journal of
Optimization, 9:112–147.
Oshman, Y. and Carmi, A. (2006). Attitude estimation
from vector obsevations usinga genetic algorithm-
embedded quaternion particle filter. Journal of Guid-
ance, Control and Dyanmics, 29:879–891.
Salcedo, J. V. and Martinez, M. (2008). Bibo stabilization of
takagi-sugeno fuzzy systems under persistent pertur-
bations using fuzzy output feedback controllers. IET
Control Theory and Applications, 2:513–523.
Shaked, U. (2003). An lpd approach to robust h
2
and h
∞
static output-feedback design. IEEE Trans. on Au-
tomat. Contr., 48:866–872.
Shaked, U. and Yaesh, I. (2007). Robust servo synthesis
by minimization of induced ℓ
2
and ℓ
∞
norms. In ISIE
2007, Vigo, Spain.
Sorenson, H. (1985). Kalman Filtering : Theory and Appli-
cation. IEEE Press.
Tanaka, K. and Wang, H. (2001). Fuzzy Control Systems
Design and Analysis - A Linear Matrix Inequality Ap-
proach. John Wiley and Sons, Inc.
Tuan, H. D., Apkarian, P., and Nguyen, T. Q. (2001). Ro-
bust and reduced-order filtering: new lmi-based char-
acterizations and methods. IEEE Trans. on Signal
Processing, 40:2975–2984.
Yaesh, I. and Shaked, U. (1991). A transfer function ap-
proach to the problems of discrete-time systems h
∞
-
optimal control and filtering. IEEE Trans. on Automat.
Contr., 36:1264–1271.
Yaesh, I. and Shaked, U. (2006). Discrete-time min-max
tracking. IEEE Trans. Aerospace and Elect. Systems,
42:540–547.
Zames, G. (1981). Feedback and optimal sensitivity : model
reference transformations, multiplicative seminorms
and approximate inverses. IEEE Trans. on Automat.
Contr., AC-26:301–320.
APPENDIX A - PROOF OF
LEMMA 1
Consider the system
x
k+1
=
¯
Ax
k
+
¯
Bw
k
, z
k
=
¯
Cx
k
+
¯
Dw
k
and define, following (Abedor et al., 1996),
ξ
k
= x
T
k+1
Px
k+1
−x
T
k
Px
k
+ λx
T
k
Px
k
−µw
T
k
w
k
.
Namely,
ξ
k
=(x
T
k
¯
A
T
+w
T
k
¯
B
T
)P(
¯
Ax
k
+
¯
Bw
k
)−x
T
k
Px
k
+λx
T
k
Px
k
−µw
T
k
w
k
.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
72

Collecting terms we have
ξ
k
= x
T
k
(
¯
A
T
P
¯
A+ λP−P)x
k
+ x
T
k
(
¯
A
T
P
¯
B)w
k
+w
T
k
(
¯
B
T
P
¯
A)x
k
+ w
T
k
(−µ
I +
¯
B
T
P
¯
B)w
k
.
Therefore, (14) guarantees ξ
k
< 0 for all w
k
and x
k
.
Defining ζ
k
= x
T
k
Px
k
and assuming x
0
= 0 and
w
T
k
w
k
< 1 we have that ζ
k+1
−ζ
k
+ λζ
k
−µw
T
k
w
k
< 0.
Namely, ζ
k
<
¯
ζ
k
where
¯
ζ
k+1
= (1 −λ)
¯
ζ
k
+ µw
T
k
w
k
.
However, using ρ := 1−λ we have
¯
ζ
k
=
k−1
∑
j= 0
ρ
k−j−1
µw
T
j
w
j
= ρ
k−1
k−1
∑
j= 0
(ρ
−1
)
j
µw
T
j
w
j
<ρ
k−1
(1−ρ
−1
)
k
1−ρ
−1
µ= µ
1−ρ
k
1−ρ
. A.1
F
rom (15) we have using Schur complements that
[x
T
w
T
](
λP 0
0 (γ−µ)I
−γ
−1
¯
C
T
¯
D
T
¯
C
¯
D
)
x
w
> 0
Namely,
z
T
k
z
k
< γ[(γ−µ)w
T
k
w
k
+λx
T
k
Px
k
] < γ[(γ−µ)+λ
¯
ζ
k
] A.2
Substituting A.1 we readily see that
z
T
k
z
k
< γ[(γ−µ)+(1−ρ)µ
1−ρ
k
1−ρ
]
= γ[γ−µ+µ−µρ
k
].
Since 0 < ρ < 1 we obtain that
z
T
k
z
k
< γ[γ −µ+ µ] = γ
2
.
APPENDIX B - PARAMETER
DEPENDENT RESULTS
In order to reduce conservatism, we replace in the
proof of Lemma 1 in Appendix A, the parameter-
independent Lyapunov function V(x, P) = x
T
k
Px
k
by
the parameter-dependent Lyapunov function ((Boyd
et al., 1994)) V(x,P
1
,P
2
) = max(x
T
k
P
1
x
k
,x
T
k
P
2
x
k
). To
ensure V(x
k
,P
1
,P
2
) > 0 we have to satisfy x
T
k
P
1
x
k
> 0
whenever x
T
k
P
1
x
k
> x
T
k
P
2
x
k
and x
T
k
P
2
x
k
> 0 whenever
x
T
k
P
1
x
k
< x
T
k
P
2
x
k
. Applying the S-procedure (Boyd
et al., 1994) we readily obtain that a sufficient condi-
tion or these requirements to hold, is the existence of
constants ρ
1
> 0 and ρ
2
> 0 so that
P
1
−ρ
1
(P
1
−P
2
) > 0 and P
2
−ρ
2
(P
2
−P
1
) > 0.
We also require that if x
T
k
P
1
x > x
T
k
P
2
x
k
then
ξ
{1},
¯
A
k
:= x
T
k
(
¯
A
T
P
1
¯
A+ λP
1
−P
1
)x
k
+ x
T
k
(
¯
A
T
P
1
¯
B)w
k
+w
T
k
(
¯
B
T
P
1
¯
A)x
k
+ w
T
k
(−µI +
¯
B
T
P
1
¯
B)w
k
< 0,
and if x
T
k
P
2
x > x
T
k
P
1
x
k
then
ξ
{2},
¯
A
k
:= x
T
k
(
¯
A
T
P
2
¯
A+ λP
2
−P
2
)x
k
+ x
T
k
(
¯
A
T
P
2
¯
B)w
k
+w
T
k
(
¯
B
T
P
2
¯
A)x
k
+ w
T
k
(−µI +
¯
B
T
P
2
¯
B)w
k
< 0.
Since these conditions are required to be satisfied
throughout the polytope, we readily obtain, using
again the S-procedure, that in addition to the con-
stant λ > 0, the existence of six additional constants
λ
i
> 0, i = 1,2,3, 4, θ
1
> 0, θ
2
> 0 establishes a suf-
ficient condition for the above inequalities to hold, if
−ξ
{1},
¯
A
i
k
−λ
1
(P
1
−P
2
) > 0, i = 1, 2
and
−ξ
{1},
¯
A
i
k
−λ
2
(P
2
−P
1
) > 0,i = 1, 2.
Following the lines of proof of Theorem 1 above, we
readily obtain the following LMIs for i = 1,2 to re-
place (21) and (22):
P
1
−λP− λ
i
(P
1
−P
2
) 0 A
T
i
P
1
−C
T
Y
T
i
0 µI B
T
i
P
1
−D
T
Y
T
i
P
1
A
i
−Y
i
C P
1
B
i
−Y
i
D P
1
>0,
λP
1
−θ
1
(P
1
−P
2
) 0 L
T
i
0 (γ−µ)I 0
L
i
0 γI
> 0, λ < 1
and
P
2
−λP− λ
i+2
(P
2
−P
1
) 0 A
T
i
P
2
−C
T
Y
T
i
0 µI B
T
i
P
2
−D
T
Y
T
i
P
2
A
i
−Y
i
C P
2
B
i
−Y
i
D P
2
>0,
λP
2
−θ
2
(P
2
−P
1
) 0 L
T
i
0 (γ−µ)I 0
L
i
0 γI
> 0, λ < 1.
We note that we have also replaced (A.2) with:
z
T
k
z
k
< γ[(γ−µ)w
T
k
w
k
+λ×max(x
T
k
P
1
x
k
,x
T
k
P
2
x
k
)].
Namely, if x
T
P
1
x > x
T
P
2
x we require
z
T
k
z
k
< γ[(γ−µ)w
T
k
w
k
+ λx
T
k
P
1
x],
whereas if x
T
P
2
x > x
T
P
1
x we require
z
T
k
z
k
< γ[(γ−µ)w
T
k
w
k
+ λx
T
k
P
2
x].
Using again the S -Procedure with additional tuning
constants θ
1
> 0 and θ
2
> 0, which add up to the pre-
viously introduced 7 tuning constants ρ
1
> 0, ρ
2
> 0,
λ > 0 and λ
i
> 0,i = 1, 2,3,4 the above results are
obtained. Note that a similar approach can be applied
also on the continuous-time results of (Salcedo and
Martinez, 2008) to reduce conservatism.
INDUCED - OPTIMAL GAIN-SCHEDULED FILTERING OF TAKAGI-SUGENO FUZZY SYSTEMS
73
