
A NOVEL VISION-BASED REACTIVE NAVIGATION STRATEGY
BASED ON INVERSE PERSPECTIVE TRANSFORMATION
∗
Francisco Bonin-Font, Alberto Ortiz and Gabriel Oliver
Department of Mathematics and Computer Science, University of the Balearic Islands
Ctra de Valldemossa Km 7.5, 07122, Palma de Mallorca, Spain
Keywords:
Mobile robots, Vision, Obstacle Avoidance, Feature Tracking, Inverse Perspective Transformation, SIFT.
Abstract:
This paper describes a new vision-based reactive navigation strategy addressed to mobile robots, comprising
obstacle detection and avoidance. Most of the reactive vision-based systems base their strength uniquely on
the computation and analysis of quantitative information. The proposed algorithm combines a quantitative
process with a set of qualitative rules to converge in a robust technique to safely explore unknown environ-
ments. The process includes a feature detector/tracker, a new feature classifier based on the Inverse Perspective
Transformation which discriminates between object and floor points, and a qualitative method to determine
the obstacle contour, their location in the image, and the course that the robot must take. The new strategy has
been implemented on mobile robots with a single camera showing promising results.
1 INTRODUCTION
Visual techniques for detecting and tracking main
scene features have been notably improved over the
last few years and applied to robot navigation solu-
tions. Zhou and Li (Zhou and Li, 2006) detected
ground features grouping all coplanar points that have
been found with the Harris corner detector (Harris and
Stephens, 1988). Lowe (Lowe, 2004) developed the
Scale Invariant Feature Transform (SIFT) method to
extract highly discriminative image features, robust
to scaling, rotation, camera view-point changes and
illumination changes. Rodrigo et al (Rodrigo et al.,
2006) estimated the motion of a whole scene com-
puting a homography matrix for every different scene
plane. Mikolajczyk and Schmid (Mikolajczyk and
Schmid, 2005) compared the performance of differ-
ent descriptors for image local regions showing that,
for different region matching approaches SIFT yields
the best performance in all tests. The Inverse Per-
spective Transformation (IPT) has been successfully
used in obstacle detection procedures. Mallot et al
(Mallot et al., 1991) analyzed variations on the opti-
cal flow computed over the Inverse Perspective Trans-
formation of consecutive frames to detect the pres-
ence of obstacles. Bertozzi and Broggi (Bertozzi and
∗
This work is partially supported by DPI 2008-06548-
C03-02 and FEDER funding.
Broggi, 1997) applied the IPT to project two stereo
images onto the ground. The subtraction of both pro-
jections generate a non-zero pixel zone that evidences
the presence of obstacles. Ma et al (Ma et al., 2007)
presented an automatic pedestrian detector based on
IPT for self guided vehicles. The system predicts new
frames assuming that all image points lie on the floor,
generating distorted zones that correspond to obsta-
cles.
This paper addresses the problem of obstacle de-
tection and avoidance for a safe navigation in unex-
plored environments. First, image main features are
detected, tracked across consecutive frames, and clas-
sified as obstacles or ground using a new algorithm
based on IPT. Next, the edge map of the processed
frame is computed, and edges comprising obstacle
points are discriminated from the rest of the edges.
This result gives a qualitative idea about the position
of obstacles and free space. Finally, a new version
of the Vector Field Histogram (Borenstein and Koren,
1991) method, here adapted to systems equipped with
visual sensors, is applied to compute a steering vector
which points towards the areas into which the vehicle
can safely move. The rest of the paper is organized as
follows: the method is outlined in Section 2, exper-
imental results are exposed and discussed in Section
3, and finally, conclusions and forthcoming work are
given in Section 4.
141
Bonin-Font F., Ortiz A. and Oliver G.
A NOVEL VISION-BASED REACTIVE NAVIGATION STRATEGY BASED ON INVERSE PERSPECTIVE TRANSFORMATION.
DOI: 10.5220/0002171301410146
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page
ISBN: 978-989-674-000-9
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
2 THE NEW METHOD
2.1 Inverse Perspective Transformation
The Direct Perspective Transformation is the first-
order approximation to the process of taking a picture.
The line that connects a world point with the lens in-
tersects the image plane and defines its unique image
point. The Inverse Perspective Transformation speci-
fies the straight line upon which the world point cor-
responding to a certain image point must lie. (Hart-
ley and Zisserman, 2003) describes the Direct and In-
verse Perspective Transformation processes and both
are also modeled in (Duda and Hart, 1973), as well as
the expressions to calculate the world coordinates for
points lying on the floor (z = 0):
x = X
0
−
Z
0
x
p
cosθ+ (y
p
sinϕ− fcosϕ)(Z
0
sinθ)
y
p
cosϕ+ f sinϕ
(1)
y = Y
0
−
Z
0
x
p
sinθ− (y
p
sinϕ− fcosϕ)(Z
0
cosθ)
y
p
cosϕ+ f sinϕ
(2)
where (x
p
, y
p
) are the point image coordinates, (x, y)
are the point world coordinates, (X
0
,Y
0
,Z
0
) are the lens
world coordinates at the moment in which the frame
has been taken, f is the focal length, and θ and ϕ are
the yaw and pitch angles of the camera, respectively.
2.2 Obstacle and Ground Points
Presuming that all image points lie on the floor (i.e.
z = 0), their (x,y) world coordinates can be calculated
using (1) and (2). This is an incorrect assumption for
points of obstacles that protrude vertically from the
floor. As a consequence, the (x, y) world coordinates
(for z = 0) of an obstacle point are different when
they are calculated from two consecutive images, and
different to the obstacle point real (x, y) world coor-
dinates. However, the (x, y) world coordinates (for
z = 0) of a ground point, are equal when they are com-
puted from two consecutive images, and equal to the
real (x, y) ground point world coordinates. Hence, as-
suming z = 0 and analyzing the distance between the
resulting (x, y) point world coordinates for z = 0, cal-
culated across two consecutive images, one can dis-
tinguish if the point belongs to an object or to the
floor:
D =
q
(x
2
− x
1
)
2
+ (y
2
− y
1
)
2
⇒
(
ifD > β⇒ obstacle,
ifD ≤ β ⇒ ground .
(3)
where (x
1
, y
1
) and (x
2
,y
2
) are the (x, y) feature world
coordinates(for z = 0) at instants t
1
and t
2
respectively
and β is the threshold for the maximum difference ad-
missible between (x
1
,y
1
) and (x
2
,y
2
) to consider both
as the same point. Ideally β should be 0.
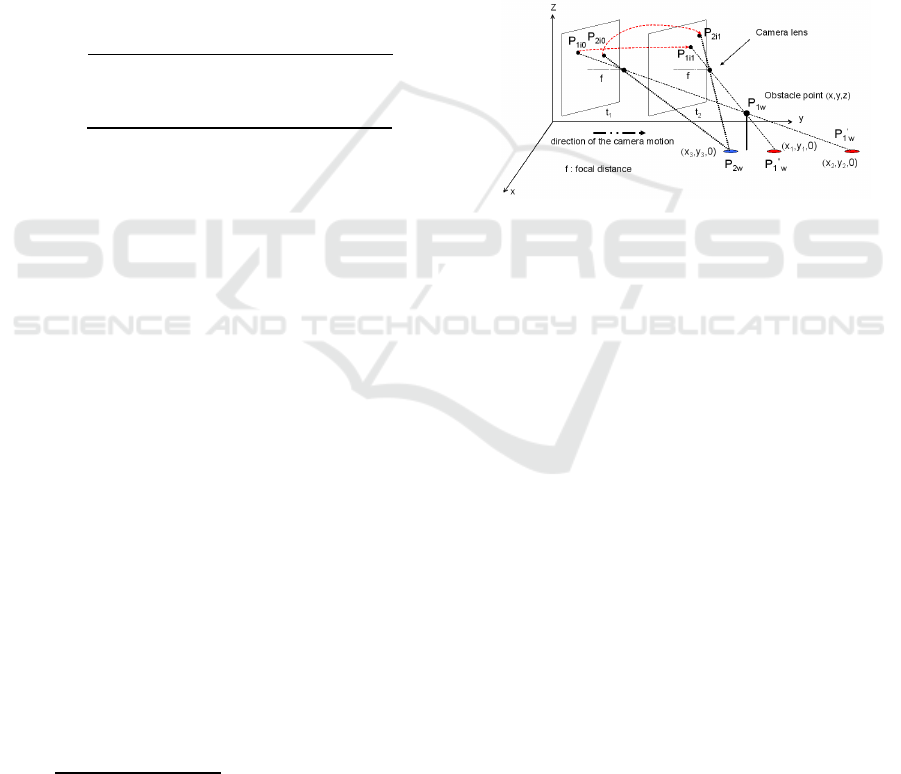
Figure 1 illustrates the idea. Two frames of a scene
are taken at instants t
1
and t
2
. Point P
2w
is on the
ground. Its projection into the image plane at instants
t
1
and t
2
generates, respectively, the image points P
2i0
and P
2i1
. The Inverse Transformation of P
2i0
and P
2i1
generates a single point P
2w
. P
1w
is an obstacle point.
Its projection into the image plane at t
1
and t
2
gen-
erates, respectively, points P
1i0
and P
1i1
. However,
the projection of P
1i0
and P
1i1
onto the ground plane
( i.e. Inverse Transformation assuming z = 0) gener-
ates two different points on the ground, namely, P
′
1w
and P
′′
1w
.
Figure 1: The IPM-based obstacle detection principle.
2.3 Feature Detection and Tracking
The first step of the obstacle detection algorithm is
to find a sufficiently large and relevant set of image
points, and establish a correspondence of all these
points between consecutive frames. SIFT features
(Lowe, 2004) have been chosen as the features to
track because of their robustness to scale changes, ro-
tation and/or translation as well as changes in illumi-
nation and view point. In order to filter out possible
wrong correspondences between points in consecu-
tive frames, outliers are filtered out using RANSAC
and imposing the epipolar constraint. After the de-
tection and tracking process, features are classified as
ground or obstacle.
Small changes in the distance threshold β can al-
ter the classification of those points which have a D
value (3) close to β. In order to decrease the sensitiv-
ity of the classifier with regard to β, all these points
are left unclassified. Additionally, in a previous train-
ing phase, and for each different scene, histograms of
D values for well classified and misclassified points
are built and analyzed. For every different scene, D
values of ground points wrongly classified as obstacle
are stored in a database. In the autonomousnavigation
phase, all object points with a D value included in that
set of stored D values of the current scene, are neither
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
142

classified. In this way, nearly all ground points clas-
sified as obstacles are eliminated, reducing the risk of
detecting false obstacles, and although some true ob-
stacle points are also removed, the remaining ones are
sufficient to permit the detection of those obstacles.
2.4 Obstacle Profiles and the Navigation
Strategy
SIFT features are usually detected at regions of high
intensity variation (Lowe, 2004) and besides, com-
monly they are near or belong to an edge. Obsta-
cles usually have a high degree of vertical edges and
have one or some points in contact with the floor. All
detected obstacle points are most likely to be con-
tained or near a vertical edge which must belong to
that obstacle. Hence, the next step of the algorithm is
the computation of the processed images edge map,
and the detection of all complete edges that comprise
real obstacle points. This permits to isolate the ob-
stacle boundaries from the rest of the edges and to
get a qualitative perception of the environment. Ob-
stacle points wrongly classified as ground can be re-
classified if they are comprised in an edge that con-
tains other obstacle points.
In order to combine a high degree of performance
in the edge map computation with a relatively low
processing time, our edge detection procedure runs
in two steps (Canny, 1986): a) The original image
is convolved with a 1D gaussian derivative, detecting
zones with high vertical gradient from smoothed in-
tensity values with a single convolution; b) A process
of hysteresis thresholding is applied. Two thresholds
are defined. A pixel with a gray level above the high-
est threshold is classified as edge pixel. A pixel with
a gray level above the lowest threshold is classified as
edge if it has in its vicinity a pixel with a gray value
higher than the highest threshold.
The proposed navigation strategy has been in-
spired by (Borenstein and Koren, 1991). Only obsta-
cles detected inside a ROI (Region of Interest) cen-
tered at the bottom of the image are considered to
be avoided. This guarantees a virtual 3-D sphere of
safety around the robot. The image ROI is in turn
divided in angular regions. Those polar directions,
corresponding to angular regions occupied by a real
obstacle boundary are labeled as forbidden and those
free of obstacle boundaries are included in the set
of possible next movement directions. This process
results in a polar map of free and occupied zones.
Obstacle-free polar regions which are narrower than
a certain threshold (determined empirically and de-
pending on the robot size) are excluded from the pos-
sible motion directions. If all angular regions are
narrower than the defined threshold, the algorithm
returns a stop order. The next movement direction
is given as a vector, pointing to the widest polar
obstacle-free zone. Positive angles result for turns to
the right and negative angles for turns to the left. The
computed steering vector qualitatively points towards
the free space and the complete algorithm gives a rea-
sonable idea of whether this free space is wide enough
to continue the navigation through it.
3 EXPERIMENTAL RESULTS
A Pioneer 3Dx mobile robot with a calibrated wide
angle camera was programmed to navigate at 40mm/s
in different environments to test the proposed strat-
egy: environments with obstacles of regular and un-
regular shape, environments with textured and untex-
tured floor, and environments with specularities or
with low illumination conditions. Operative param-
eter settings: image ROI = 85 pixels; for the hystere-
sis thresholding: low level= 40 and high levels= 50;
camera height= 430mm; ϕ = −9
◦
; initial θ = −2
◦
,
and finally, f = 3.720mm. For each scene, the com-
plete navigation algorithm was run over successive
pairs of 0.56-second-separationconsecutiveframes so
that the effect of IPT was noticeable. Increasing the
frame rate decreases the IPT effect over the obstacle
points, and decreasing the frame rate delays the ex-
ecution of the algorithm. Frames were recorded and
down-sampled to a resolution of 256×192 pixels, in
order to reduce the computation time. All frames
were also undistorted to correct the error in the im-
age feature position due to the distortion introduced
by the lens, and thus, to increase the accuracy in the
calculation of the point world coordinates.
In order to assess the classifier performance ROC
curves were computed, defining obstacle points clas-
sified as obstacle as true positives (TP), obstacle
points classified as ground as false negatives (FN),
ground points classified as floor as true negatives
(TN) and ground points classified as obstacles as false
positives (FP). The AUC (Area Under the Curve)
were calculated as a measure of success classifica-
tion rate, suggesting success rates greater than 93%
(Bonin-Font et al., 2008). The β operational value
(3) was obtained for every scene minimizing the cost
function f(β) = FP(β) + λFN(β). During the ex-
periments, λ was set to 0.5 to prioritize the minimiza-
tion of false positives over false negatives. The value
of f(β) was calculated for every pair of successive im-
ages, changing β. For a varied set of scenes differing
in light conditions and/or floor texture, the optimum
β had a coincident value of 20mm.
A NOVEL VISION-BASED REACTIVE NAVIGATION STRATEGY BASED ON INVERSE PERSPECTIVE
TRANSFORMATION
143
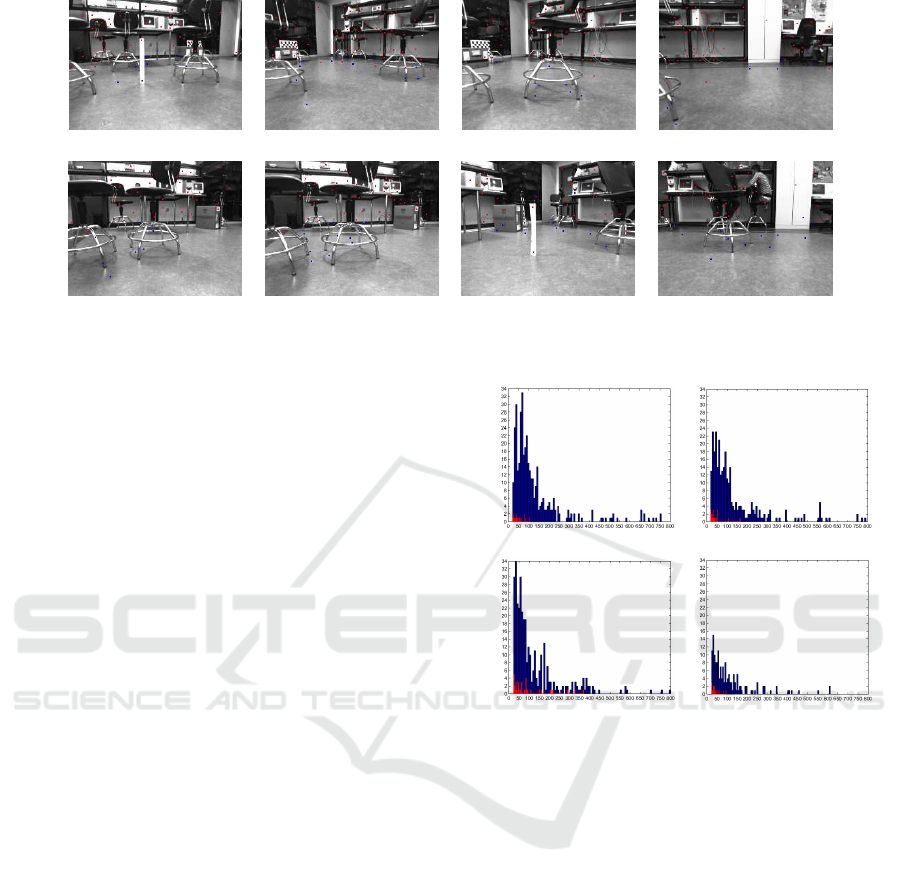
(a) (b) (c) (d)
(e) (f) (g) (h)
Figure 2: Scene 1. (a) to (d)- Experiment 1. (e) to (h)- Experiment 2: Object and floor points after the filter.
Images (a), (b), (c) and (d) of figure 2 show the
undistorted second frame of several pairs of consecu-
tive images, recorded and processed on-line. Images
show SIFT features classified as ground (blue) and
classified as obstacles (red). Every image was taken
just before the robot had to turn to avoid the obstacles
it had in front. Notice that all four pictures present a
few false positives on the floor.
Histograms of D values for TP (in blue) and FP
(in red) are presented in figure 3. Plot (a) corre-
sponds to scene 1 (figure 2), plot (b) to scene 2, plot
(c) to scene 3 and plot (d) corresponds to scene 4.
Scenes 2,3 and 4 are shown in figure 4. These his-
tograms count false and true positives for different D
values, in all frames recorded and computed by the
algorithm during a complete sequence. Although his-
tograms belong to environments with different light-
ing conditions or floor textures, and scenarios with
inter-reflections or specularities, results were com-
monly similar: most of the true positives presented
D values between 20mm and 300mm, and the ma-
jority of false positives had D values between 20mm
and approximately 80mm. All positives with D values
between 20mm and 80mm were filtered and left un-
classified. This filtering process increases AUCs until
the 96%, however, obstacle points near the floor have
more probabilities of been miss-classified than others
since their D value can be lower than 20mm.
Pictures (e) to (h) of figure 2 were taken dur-
ing a second experiment through the environment of
scene 1. In this experiment, the filter outlined in
the previous paragraph was applied. Notice that all
false positives have been eliminated. This reduces the
risk of detecting false obstacles but maintains a suffi-
cient number of true positives to detect the real obsta-
cles. After the process of feature detection, tracking,
and classification, the algorithm localizes every ob-
(a) (b)
(c) (d)
Figure 3: Histograms of D values: TP (blue) and FP (red).
ject point in the edge map of the second frame, and
then searches for all edge pixels which are inside a
patch window of 8×13 pixels, centered in the feature
image coordinates. Every edge is tracked down start-
ing from the object point position until the last edge
pixel is found, and considering this last edge pixel to
be the point where the object rests on the floor. This
process results into the identification of the object ver-
tical contours. The consecutive execution of the com-
plete algorithm using successive image pairs as input
results in a collection of consecutive steering vectors
used as the continuous motion orders. After every
robot turn, the value of the camera yaw angle is up-
dated, adding the turn angle to the previousyaw value.
The camera world coordinates are calculated compos-
ing the robot orientation and its center world coordi-
nates obtained via dead reckoning, with the relative
camera position respect to the center of the robot.
Pictures from (a) to (d), (i) to (l) and (p) to (s)
in figure 4 show the second frame of different pairs
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
144

of consecutive images, recorded and processed dur-
ing the navigation through the scenarios 2, 3 and 4,
respectively. Every image was taken before the robot
had to turn to avoid the frontal obstacles, and show
obstacle (in red) and ground points (in blue). Scene
2 presents inter-reflections, specularities, and a lot of
obstacles with regular and irregular shapes. Scene
3 shows a route through a corridor with a very high
textured floor, columns and walls. Scene 4 presents
bad illumination conditions, a lot of inter-reflections
on the floor, and some image regions (walls) with al-
most homogeneous intensities and/or textures, which
results in few distinctive features and poorly edged
obstacles. Walls with a very homogeneous texture
and few distinctivefeatures can present difficulties for
its detection as an obstacle. In all scenes, all obsta-
cle points with a D value between 20mm and 80mm
were left unclassified, except in scene 4, where, only
those obstacle points with a D value between 20mm
and 45mm were filtered out. Pictures (e) to (h), (z) to
(o) and (t) to (x) of figure 4 show the vertical contours
(in orange) comprising obstacle points. See attached
to every picture the angle of the computed steering
vector. For example, in picture (x) objects are out of
the ROI, then, the computed turn angle is 0
◦
(follow
ahead). In picture (e) the obstacles are partially inside
the ROI, so the robot turns to the right (40
◦
). De-
spite scene 4 presents a poor edge map and few SIFT
features, the resulting steering vectors still guide the
robot to the obstacles-free zone. Plots (1) to (4) show
an illustration of the environment and the robot tra-
jectory (blue circle: the starting point; red circle: the
final point) for scenes 1, 2, 3 and 4, respectively. In all
scenes, all features were well classified, obstacle pro-
files were correctly detected and the robot navigated
through the free space avoiding all obstacles. The
steering vector is computed on the image and then it
is used qualitatively to guide the robot.
4 CONCLUSIONS
This paper introduces a new vision-based reactive
navigation strategy addressed to mobile robots. It
employs an IPT-based feature classifier that distin-
guishes between ground and obstacle points with a
success rate greater than 90%. The strategy was
tested on a robot equipped with a wide angle camera
and showed to tolerate scenes with shadows, inter-
reflections, and different types of floor textures or
light conditions. Experimental results obtained sug-
gested a good performance, since the robot was able
to navigate safely. In order to increase the classifier
success rate, future research includes the evaluation
of the classifier sensitivity to the camera resolution or
focal length. The use of various β values, depending
on the image sector that D is being evaluated, can also
increase the classifier performance.
REFERENCES
Bertozzi, M. and Broggi, A. (1997). Vision-based vehicle
guidance. Computer, 30(7):49–55.
Bonin-Font, F., Ortiz, A., and Oliver, G. (2008).
A novel image feature classifier based on in-
verse perspective transformation. Technical re-
port, University of the Balearic Islands. A-01-2008
(http://dmi.uib.es/fbonin).
Borenstein, J. and Koren, I. (1991). The vector field his-
togram - fast obstacle avoidance for mobile robots.
Journal of Robotics and Automation, 7(3):278–288.
Canny, J. (1986). A computational approach to edge detec-
tion. IEEE TPAMI, 8(6):679 – 698.
Duda, R. and Hart, P. (1973). Pattern Classification and
Scene Analysis. John Wiley and Sons Publisher.
Harris, C. and Stephens, M. (1988). Combined corner and
edge detector. In Proc. of the AVC, pages 147–151.
Hartley, R. and Zisserman, A. (2003). Multiple view geom-
etry in computer vision. Cambridge University Press,
ISBN: 0521623049.
Lowe, D. (2004). Distinctive image features from scale-
invariant keypoints. International Journal of Com-
puter Vision, 60(2):91–110.
Ma, G., Park, S., Mller-Schneiders, S., Ioffe, A., and Kum-
mert, A. (2007). Vision-based pedestrian detection -
reliable pedestrian candidate detection by combining
ipm and a 1d profile. In Proc. of the IEEE ITSC, pages
137–142.
Mallot, H., Buelthoff, H., Little, J., and Bohrer, S. (1991).
Inverse perspective mapping simplifies optical flow
computation and obstacle detection. Biological Cy-
bernetics, 64(3):177–185.
Mikolajczyk, K. and Schmid, C. (2005). A perfor-
mance evaluation of local descriptors. IEEE TPAMI,
27(10):1615–1630.
Rodrigo, R., Chen, Z., and Samarabandu, J. (2006). Feature
motion for monocular robot navigation. In Proc. of the
ICIA, pages 201–205.
Zhou, J. and Li, B. (2006). Homography-based ground de-
tection for a mobile robot platform using a single cam-
era. In Proc. of the IEEE ICRA, pages 4100–4101.
A NOVEL VISION-BASED REACTIVE NAVIGATION STRATEGY BASED ON INVERSE PERSPECTIVE
TRANSFORMATION
145

(a) (b) (c) (d)
(e) 40
◦
(f) 65
◦
(g) 50
◦
(h) 0
◦
(i) (j) (k) (l)
(z) 0
◦
(m) −41.5
◦
(n) −43.5
◦
(o) 0
◦
(p) (q) (r) (s)
(t) 48
◦
(u) −39
◦
(w) −43.5
◦
(x) 0
◦
stools
cilinder
stools
lockers and shelves
chessboard
stool
vertical plank
stool
stool
lockers
and shelves
chair
chessboard
front door
lab. wood door
door
column
access to corridor
front wall
with locks and
shelves
1500
1000
500
0
-500
-500 0 500 1000
1500
2000
2500
2000
(1) (2) (3) (4)
Figure 4: (a) to (d) Scene 2, (i) to (l) Scene 3, (p) to (s) Scene 4. (e) to (h), (z) to (o) and (t) to (x), vertical contours of Scene
2, 3 and 4, respectively. (1) to (4): robot trajectories.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
146
