A PRACTICAL APPROACH FOR COMBINATORIAL FUZZY

LOGIC CONTROL DESIGN

Arturo V. Téllez, Luis A. V. Villa, Herón L. Molina, Oscar N. Camacho and Romeo P. Urbieta

Centro de Investigación en Computación, Instituto Politécnico Nacional

Juan de Dios Batiz Ave. s/n, Nueva Industrial Vallejo, Mexico City, Mexico

Keywords: Fuzzy Logic Controller, Fuzzy Sets Adaptation, Combinatorial Design, FPGA, Fast Prototyping, Hardware.

Abstract: This paper presents the architecture development of a Fuzzy Logic Controller (FLC), using combinatorial

design implemented on a Field Programmable Gate Array (FPGA). This architecture is based on

combinatorial basic modules that enable to increase and improve the entire system performance, by means

of replication technique, which is widely used in computer architecture, and help to fit the particular

application needs. Recent FPGA technology let us use fast combinatorial circuits for complex designs with

parallelism for increasing the FLC performance and it is possible to take it up again as a practical way to

build FLC for any process, approaching the fast prototyping advantages and easing the scaling to increase

the control accuracy.

1 INTRODUCTION

A FLC can be implemented in software easily and

executed in a microprocessor, a microcontroller, or a

general purpose computer. Though software- based

FLC are cheaper and flexible, there are some

difficulties when control systems require high data

processing. The use of FPGA has been profitable

when talking about versatility to make any digital

design by means of costs and design time. In

principle, the implementation of FLC is not based on

the mathematic model of the plant, but this kind of

system is very effective to control a process where

the transfer function is not known, instead the

control action is based on the extern influence and

simple decisions based on a knowledge base

acquired with experience, the same way a human

would do it, exploiting the heuristic ability. There

have been so many FLC implementations since the

first hardware one appeared (Togai, 1986), which

used complex designs with sequential circuits

because of the high hardware resource and delay

time costs about combinatorial design. A large

quantity of FLC architectures, derived from

Computing Architecture. These architectures are

classified by its processing way. There are

sequential, combinatorial (Manzoul, 1992), parallel,

pipelined and mixed models. Some designers prefer

to implement these operations to calculate a

parameter of the FLC every time it is necessary

(Gaona, 2003); this technique is called Runtime

Computation (RTC). But some designs use extern

elements like memories, sometimes called Look Up

Tables (LUT), to calculate FLC parameters by

anticipation; this another technique is called Look

Up Computation (LUC) and represents a good way

to improve the timing (Vasantha, 2005; Singh, 2003;

Deliparaschos, 2005). It is a dare to play with these

architectures and techniques to make a balanced

FLC design, by which it is necessary to change the

way of designing algorithms to describe a FLC.

This paper shows a practical approach of FLC

combinatorial architecture in order to make simple

construction modules and easy upgrading using a

reprogrammable device, FPGA.

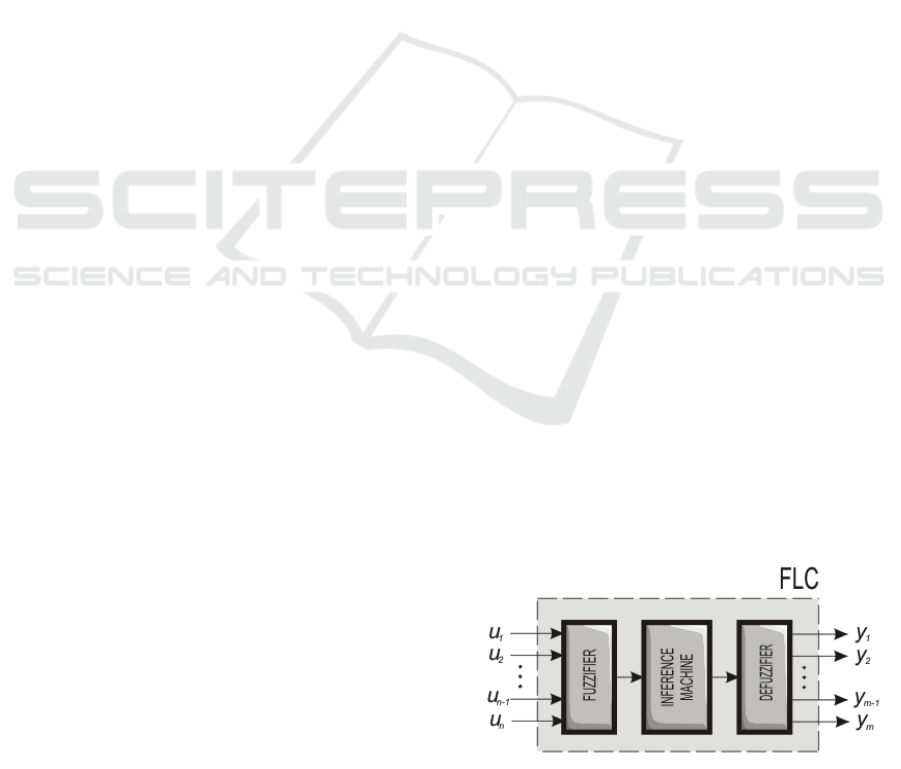
Figure 1: Fuzzy Logic Controller.

343

V. TÃl’llez A., A. V. Villa L., L. Molina H., N. Camacho O. and P. Urbieta R.

A PRACTICAL APPROACH FOR COMBINATORIAL FUZZY LOGIC CONTROL DESIGN.

DOI: 10.5220/0002172303430346

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page

ISBN: 978-989-8111-99-9

2 SYSTEM DESCRIPTION

Assume 



as the inputs to the FLC and 



as the

outputs. Figure 1 shows a FLC which consists of

three basic stages: Fuzzification, Inference Machine

and Defuzzification. The Fuzzification stage consists

of fuzzy sets. Each fuzzy set converts every crisp

input into several fuzzy values or membership

values. The Inference Machine contains the

behaviour of the FLC and it is built with MIN-

MAX modules. These rules have simple inferences

of the type IF- THEN. Also, the Defuzzification

stage converts these inferred values onto crisp

values, by means of statistical calculations, which

represent the control action over the actuator. The

next steps are required for build a FLC (Tellez,

2008):

1. Establish whatever the designer want to

control and which variables will be related

to get it.

2. Define the number of inputs and outputs of

the FLC based on the last step.

3. Define the number of membership

functions or fuzzy sets for each input and

output based on the last step and define

their shape based on the process

characteristics and operation range of the

FLC (discourse universe).

4. Set the FLC configuration by means of the

fuzzy inference rules according to the

wished operation and based on the expert

knowledge about the process.

5. Build the fuzzifier with simple membership

functions simply by replication

(trapezoidal, triangular, S, Z).

6. Build the inference machine based on step

4, by means of MIN- MAX modules using

the building steps shown in section 2.2.

7. Once inference machine is ready, build the

defuzzification stage by means of

multiplication and division modules using

parallelism.

8. Finally, FLC can be implemented on

FPGA.

For the FLC implementation it was used VHDL,

Xilinx ISE 6.3i, Mentor Graphics Modelsim Xilinx

Edition III 6.0a. It is used Xilinx Spartan 3

XC3S200–5FT256 FPGA Starter Kit. In order to

verify the FLC performance, it was necessary to

make a simulation using the Fuzzy Toolbox of

MATLAB and build a control system with

SIMULINK.

Figure 2: Isosceles triangular membership function shape.

Figure 3: Several hardware suitable membership

functions.

2.1 Fuzzification

The fuzzification stage comprises a set of fuzzifiers

attached to every input variable; each one parallel

from the others and their performance does not

depend on the others either. We assume that all

membership functions shape will be triangular,

trapezoidal, S and Z, because they are the easiest to

implement in hardware as shown in the Figure 2.

These modules convert a crisp digital value into a

membership digital value, according to two

parameters: the CENTER and the APERTURE.

These two parameters of the membership functions

accomplish the RTC technique in order to make the

online adaptation and the FLC tuning.

These functions may have several shapes as

shown in Figure 3 and the interconnection seems

like it follows in Figure 4. Next section describes the

inference machine construction according to a set of

steps using Mamdani operation.

Figure 4: Fuzzifier.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

344

Figure 5: MIN- MAX modules.

Figure 6: Inference machine stage construction.

2.2 Inference Machine

Let us define a premise as the input data involved

with the control, it means that an involved input will

be considered to decide which control action will be

taken. A consequence is a result of the inference, the

output data of inference machine, it means the

decision that FLC will take based on the premises. A

fuzzy rule set is the FLC configuration of the simple

form:

12, … , 

12, … , 

A Mamdani inference machine consists of

MAX-MIN (Figure 5) modules interconnected

according to the fuzzy rule set (Patyra, 1996). A

MAX-MIN structure of an inference machine has

MIN modules in parallel. Unlike the MAX modules

are in cascade, as shown in Figure 6.

2.3 Defuzzification

This stage obtains a crisp output by means of output

fuzzy sets, sometimes called Centroid method. The

calculation of the centroid is made using the

membership values









,



,…,





, obtained from

the inference engine, and the output fuzzy set

centers





. It is often considered as singleton

membership function, because of its computational

simplicity and because this statistical calculation is

independent of the output fuzzy set shapes.









∑

















,



,…,









∑











,



,…,









(1)

This defuzzifier needs a division calculation, as

seen in the Equation 1, which results

computationally expensive when trying to divide 2

bits multiplication result numbers, which is not

practical neither cheap computationally. In order to

avoid the  multiplication before the division, so

part of Equation 1 was implemented this way:













∑











,



,…,









(2)

Then, the result σ



(Equation 2) is multiplied by

every membership value obtained from the inference

machine. To get this, it was needed to implement a

combinatorial non-restoring division (Oberman,

1997) modified to obtain a fixed point 2b bits

quotient, becauseσ



1, as shown in Figure 7.

3 IMPLEMENTATION AND

VERIFICATION

As example of application, a FLC for a DC servo is

implemented, as mentioned above, in order to verify

the correct performance of the FLC.

Figure 7: Defuzzification stage.

A PRACTICAL APPROACH FOR COMBINATORIAL FUZZY LOGIC CONTROL DESIGN

345

The control system was built in MATLAB Fuzzy

Toolbox first, creating a fuzzy inference system by

software (FIS). As an example, suppose that we

want to implement a 2×1 fuzzy system for a DC

servo, which uses nine rules because it has three

fuzzy sets per input (position error eP: NE, ZE, PE.

position error change velocity cP: NC, ZC, PC) and

output (voltage <volts>- V: NV, ZV, PV), shown in

the Figure 7, which are the following:

IF eP is NE AND cP is NC THEN V is NV

IF eP is NE AND cP is ZC THEN V is NV

IF eP is NE AND cP is PC THEN V is NV

IF eP is ZE AND cP is NC THEN V is NV

IF eP is ZE AND cP is ZC THEN V is ZV

IF eP is ZE AND cP is PC THEN V is PV

IF eP is PE AND cP is NC THEN V is PV

IF eP is PE AND cP is ZC THEN V is PV

IF eP is PE AND cP is PC THEN V is PV

Then, it was provided a test bench which

consists of 25 values and describes several input

situations but due to space it is not explained in this

paper. Also, FLC tuning was made changing the

membership function parameters of inputs and

outputs. Table 1 shows all timing and resources in

FPGA used for every implemented module built for

DC servo FLC example. DC servo FLC needs 84 ns

to make a single inference. Then, its processing data

rate is 11.9 MFLIPS.

4 CONCLUSIONS

FLC architecture was designed using RTC

combinatorial arithmetic modules. In order to get

this, it was supplied to designer a practical approach

for FLC design, using a study case (DC servo).

Those developed modules were implemented in

FPGA and it was possible to verify the FLC

performance compared with the FIS simulated with

MATLAB. We proved that this architecture has the

capability of grow modularly. This modularity may

be approached using a FIS to VHD language

interpreter that simply generates the proper HDL

program, using the basic modules presented in this

paper, regardless the used technology, based on the

MATLAB *.fis configuration file.

ACKNOWLEDGEMENTS

Research supported by the Instituto de Ciencia y

Tecnología ICyTDF funding (award No. PICCT08-

22) and by matching funding by IPN (award No.

SIP/DF/2007/143).

Table 1: FPGA timing and resource results obtained for

DC servo control.

Algorithm Delay (ns) LUT

16 bits non-restoring division 48.50 644

Modified 8 bits non-restoring

division

28.83 208

8 bits restoring division 28.84 124

8 bits multiplication 13.17 36

Isosceles triangle MF

36.70

14.51

251

S-step MF 36.70 249

Z-step MF 36.70 251

Fuzzifier 37.42 755

Defuzzifier 41.49 677

Mamdani inference machine 19.32 242

MIN-MAX operations 9.36 16

FLC 84.01 2689

REFERENCES

Téllez, A., 2008. Fuzzy Logic Controller Architecture

using Combinatorial Logic, Instituto Politécnico

Nacional. Centro de Investigación en Computación.

Mexico City.

Patyra, M. J.; Mlynek, D.M.; “Fuzzy logic:

implementation and applications;” Wiley; 1996.

Oberman, S. F.; Flynn, M. J.; “Division Algorithms and

Implementations;” IEEE Transactions on Computers;

Aug 1997; Vol 46, No. 8; pp. 833–854.

Togai M.; Watanabe H.; “Expert system on a chip: An

engine for real–time approximate reasoning;” IEEE

Expert Syst. Mag., 1986, pp. 55–62, Volume 1.

Vasantha Rani, S.P.J.; Kanagasabapathy, P.; Sathish

Kumar, A.; “Digital Fuzzy Logic Controller using

VHDL;” INDICON, 2005 Annual IEEE, 11–13

December 2005, pp. 463–466.

Singh, S.; Rattan, K.S.; “Implementation of a fuzzy logic

controller on an FPGA using VHDL;” Fuzzy

Information Processing Society, 2003. NAFIPS 2003.

International Conference of the North American

24–26 July 2003, pp. 110–115.

Deliparaschos, K.M.; Nenedakis, F.I.; Tzafestas, S.G.; “A

fast digital fuzzy logic controller: FPGA design and

implementation;” Emerging Technologies and Factory

Automation, 2005. ETFA 2005. 10

IEEE

Conference, 19–22 September 2005, Volume 1.

Gaona, A.; Olea, D.; Melgarejo, M.; “Sequential Fuzzy

Inference System Based on Distributed Arithmetic;”

Computational Intelligence for Measurement Systems

and Applications, 2003. CIMSA ’03. 2003 IEEE

International Symposium, 29–31 July 2003, pp. 125–

129.

Manzoul, M.A.; Jayabharathi, D.; “Fuzzy Controller on

FPGA Chip;” Fuzzy Systems, 1992., IEEE

International Conference, 8–12 March 1992, pp.

1309–1316.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

346