
QUANTIFIED ONTOLOGIES FOR REAL LIFE APPLICATIONS
Lucia Vacariu
1
, George Fodor
2
1
Department of Computer Science, Technical University of Cluj Napoca, 26 Baritiu str, Cluj Napoca, Romania
2
ABB AB Process Automation, Vasteras, Sweden
Gheorghe Lazea, Octavian Cret
Department of Automation, Department of Computer Science, Technical University of Cluj Napoca, Cluj Napoca, Romania
Keywords: Merging Ontologies, Symbolic Approaches to Control, Semantic Services, Mobile Robots.
Abstract: Industrial applications are using run-time symbolic approaches only when formal methods can assign useful
meaning to symbols by computationally inexpensive algorithms. However, most reasoning methods are
either computationally prohibitive or may compute indefinitely; thus such methods have limited use in
industrial applications. In many practical situations, the uncertain environment in which an “intelligent”
control system acts consists of the symbolic space of some other “intelligent” control system, both
networked in the same name space. The result of such interaction is to establish relations between
heterogeneous vocabularies and reasoning agents, and between symbols and the physical environment in
which the connected systems act. This paper introduces and motivates the necessity for on-line
quantification of the degree to which symbols in a system have their intended meaning.
1 INTRODUCTION
The theory presented here has relevance for
distributed real-time systems such as those used in
multi-robot applications or in distributed
manufacturing industries. These systems have a
large set of symbols in the form of names for
components, signals, process states or configuration
parameters. Heterogeneity manifests by units being
of different specialization and of different make.
Having the right meaning of each symbol is essential
for a correct operation of the system. The costs for
matching all signals, communication protocols and
sub-products during a tender process for a complex
system turn out to be a significant part of the total
cost of the system. Moreover, after delivery,
ensuring that the final system behaves according to
specifications can be a lengthy and highly qualified
process. The solution to this problem is to establish
an ontology for the given industrial domain. These
tools need to reduce symbol complexity by
automatic information processing, such as via
semantic web and ontological languages.
It is an uncommon situation today that such
configuration tools work across dissimilar firms or
markets, though many core technologies and
standards are available. On a theoretical level, the
operations needed, such as ontology merging,
alignment composition, union and intersection are
still under research (Furst, 2008).
We stress here that formal design verification
cannot replace the ontological compliance presented
in this paper: even a perfectly designed system that
is formally proven to follow a design might
encounter a complex environment that does not
follow the assumptions in the specification.
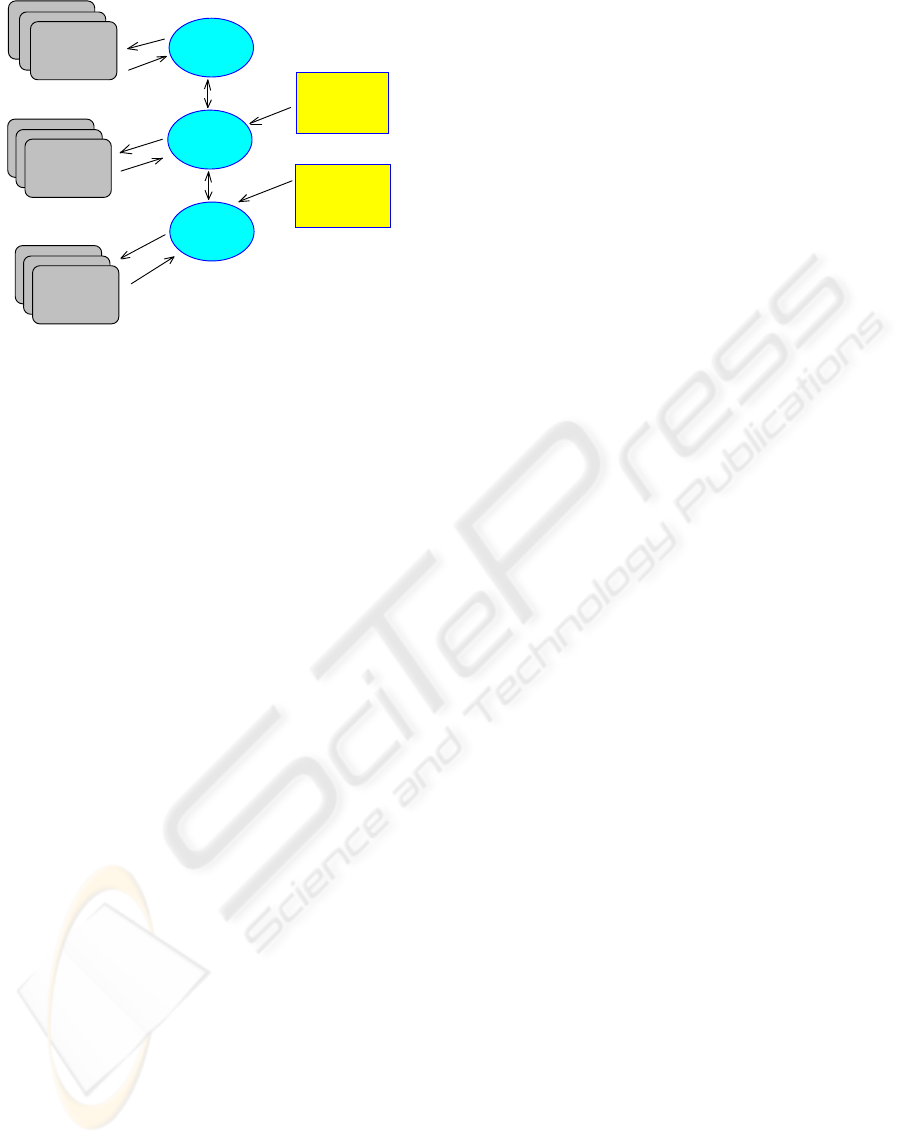
Seen as software architecture, ontologies are
implemented at the current level of technology as
services. These can be organized as local services in
each unit or as a combination of a hierarchic set of
services – local and specialized - with indirections
provided by name servers. Without specifying
details, we call in this paper a generic ontology
service as the “Industrial Ontology Server” (IOS)
(Figure 1).
Practically, an IOS should be able to infer the
structure of any type of distributed industrial
application. Of course, this is a very ambitious
claim, well beyond the forefront of what is available
today in academia or industrial research institutes.
383
Vacariu L., Fodor G., Lazea G. and Cret O. (2009).
QUANTIFIED ONTOLOGIES FOR REAL LIFE APPLICATIONS .
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 383-386
DOI: 10.5220/0002176103830386
Copyright
c
SciTePress
Manufacturers
Control
Equipment
System
Integrators
and OEM
On-line
Control
System
Compliance
Service
Endorsement
Service
Ontology
Broker
Compliance
Broker
Endorsement
Broker
Bridge
Bridge
Publish
Publish
Publish
Fwd Invoke
Fwd Invoke
Fwd Invoke
Figure 1: Federated Service Architecture IOS.
The solution proposed here is to use a minimal,
uniform ontology associated to products and that
each actual systems to update automatically the
required operational and dynamic information into
IOS-es. With this approach, biding costs would be
substantially reduced and market participation would
guarantee more objectivity and flexibility.
Clearly a multi-agent system architecture could
implement such requirements. Tools such as JADE
(Java Agent DEvelopment framework) with Protégé
(Ontology editor and knowledge-base framework)
could handle the design of systems based on a
common design ontology (Tomaiuolo et al., 2005).
2 SOME RELEVANT
TECHNOLOGIES AND
THEORIES
An IOS is relevant if it considers all levels of an
industrial unit included in a system: from signals and
actuators, up to overall goals, including states,
alarms, resource allocation, synchronization with
other units, etc.
2.1 Ontologies in Process Control
Ontologies for automation and process control
applications have several specific layers. At the
design phase, there is available a formal or informal
description of the domain and of the constraints of
the design (Design Model). The standard for
IEC61499 prescribes the Engineering Support
System (ESS) that can perform certain syntactic and
semantic verifications. Valuable research is being
conducted for improving ESS tools (Thamboulidis,
Koumoutsos, and Doukas, 2007).
The framework (middleware) in which the
program, agents or components execute has own
ontology and semantics that limits what the
application program can execute (Execution Model).
Application Ontology. This is the ontology that
effectively decides on goals and actuation. The
domain of discourse is not necessarily the same as
the domain used for the design ontology.
Visualized Ontology. The ontology is typically
visualized on a human-readable interface. The
domain of discourse, taxonomy among objects and
object properties are represented graphically.
Automatic generation of visualization using as input
ontologies expressed in XML/RDF would be an
important advance in technology.
Communicated Ontology. From the execution
model and design data, system designers extract an
ontology used for communicating among
cooperating systems. This ontology may not have
the domain of the Design Model, nor of the
Execution Model.
Ontology does not enter in a formal, verified way
in the design of large control products, as tools are
not mature enough. Another conclusion is that a
system has several ontologies that should be aligned.
There are no commercial tools that can align
ontologies. Interesting research results are reported
using category theory (Zimmermann et al., 2006).
3 METRICS FOR ON-LINE
ONTOLOGIES
3.1 The Decision-Control Space
Essential for taxonomy of process control systems is
the type of actuators used. Actuators are performing
changes in the real world; their semantics is
determined by physical laws.
Independently of the software architecture type,
a control system has two essential parts: (a) a
decision (information) level and (b) a physical,
energy-related level of actuator and plant changes.
All the relevant information from sensed signals
used for decision forms a hyperspace with each
coordinate being one kind of decision information.
Let this space be H with N dimensions,
H
∈
R
N
.
Chains of decisions generate chains of action
trajectories
T
i
(i
=
1,...,
M
) in this space.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
384

Trajectories may not be continuous as disturbances
create ‘jumps’ from one possible trajectory to
another. A valid place on this trajectory is often not
a point but a hyper-sphere (a topology) since usually
control decisions are taken within intervals and not
on discrete points.
In traditional control, the space of all relevant
signals is called a state space and the trajectory a
goal path. Each point reached during control in the
state space is a state. For each state space, a
controller (or agent or component) has mapped a
decision procedure that result in some action being
taken. We are not concerned here with what kind of
decisions or reasoning a controller is doing, but only
with the mapping between actions u
i,j
and spheres
h
i,j
. Here the variable u denotes an action, and the
variable h denotes a sphere in H. We call the pair S
i,j
= (h
i,j
, u
i,j
) as a state and use first index to denote the
sphere i and the second index to denote a goal path j.
3.2 State Semantics
The active state is the one currently materialized by
sensors. Even if the system consists of many agents
or components, there is always a unique active state
since the hyperspace covers the whole possible
space. However, there may be multiple actions
corresponding to each active state. We represent
here all actions for one point in the hyperspace as a
single action. Some typical state transitions we are
interested in are the following: case (1) - normal
control with no disturbances, case (2) - control with
disturbances and case (3) - lockout.
Performing no action may be a legal, correct
operation of the controller, however if inaction is
due to decision lockout, then this case is distinct and
should be detected.
We seek here moreover to quantify the level of
true semantics states have.
3.3 Quantifying State Semantics
3.3.1 Intra-state Distance
The degree for how “strong” is a state with a current
place h
i,j
in the space H is the inverse of the distance
from h
i,j
to the centre of the sphere intended for that
state. Therefore, closer h
i,j
is to the state sphere
boundary, less correlation it has with the current
state and its action. This is the typical situation when
the true state is somewhere in between two states,
none fully reached; fuzzy logic can quantify and
correct this situation (Grantner and Fodor, 2002).
For a measured probability distribution Q, the
Kullback Leibler divergence of Q from P is:
D
KL
(P ||Q) = P(i)log
P
(i)
Q(i)
i
∑
(1)
3.3.2 Inter-state Endorsement
The following levels of endorsement for a state are
defined to characterize how well predictions are
built into the semantics of a state materialize.
Void-Endorsement. A state is void-endorsed if it is
materialized. That means for a state S
i,j
= (h
i,j
, u
i,j
)
ve(S
i,j
) iff (h
i,j
∧ u
i,j
)
(2)
This is the simplest form of endorsement, but it
tells an important think: that the program semantics
about the environment matches at least once a real
instance of the environment. The properties matched
are those in h
i,j
.
Weak State Endorsement. A state is weakly
endorsed if a consecutive state of a void-endorsed
state placed on the same goal path is weakly
endorsed at the next instance of time.
we(S
i,k
) iff ve(S
i,k
) ∧ O ve(S
j,k
)
(3)
Here ‘O’ is the ‘next time’ logical operator; both
states are on the same path T
k
as the second index k
shows. A we() state is not a goal state. Weak
endorsement means that if a state has materialized
and the controller has executed an action at that
state, then the expected outcome really turned out to
be true in the environment.
Strong State Endorsement. A state is strongly
endorsed if a consecutive state on the same path
materializes and both states are weakly endorsed.
se(S
i,k
) iff we(S
i,k
) ∧ O we(S
j,k
)
(4)
A se() state is again not a goal state. This state
endorsement tells that after a state materialize and
the action executed, a next expected state indeed
materializes as well and moreover the action from
that second state has the expected effects.
3.3.3 Goal Path Endorsement
Goal paths are endorsed in similar way as states.
Void Endorsed Goal Path. A goal path T
k
is void
endorsed if there exists a state that is not the goal
state of the path and which is weakly endorsed:
QUANTIFIED ONTOLOGIES FOR REAL LIFE APPLICATIONS
385

vpe(T
k
) iff
∃
i ve(S
i,k
)
(5)
A void-endorsed goal path has some h
i,j
of some
state that materializes in the environment, moreover
the corresponding action is being executed, but there
is no evidence that any of the following expected
states on the same goal path have been materialized.
Note that there may be states that are not on any goal
path, so a void endorsed state may not necessarily
mean a void endorsed goal path.
Weakly Endorsed Goal Path. A goal path T
k
is
weakly endorsed if there exists some state on the
goal path that is weakly endorsed and which is not
the goal state of the path.
wpe(T
k
) iff ∃i we(S
i,k
)
(6)
A weakly endorsed goal path has at least one
state that when acting on the path, get expected
effects on the same goal path. However, it is not sure
that the expected state has the required quality that
even its action will get expected results and thus the
semantics of the second reached states is not entirely
sure.
Strongly Endorsed Goal Path. A goal path T
k
is
strongly endorsed if there exists a state that is
strongly endorsed on the goal path.
spe(T
k
) iff ∃i se(S
i,k
)
(7)
More generally, a goal path is n-strongly
endorsed if there are n states which are strongly
endorsed on the path. N-strong endorsement tells
that many states on the goal path are semantically
right, but there may be disturbances that materialize
states interleaved with disturbances, on some other
goal paths. The condition that one full goal path is
traversed without interruption is given by the full-
goal path endorsement: a goal path is full-goal
endorsed if all the states of the goal path materialize
in expected order up to the goal state. Clearly all
states of a path that has full-goal endorsement are
strongly endorsed, except the goal state and the state
immediately before the goal state that is weakly
endorsed.
3.3.4 Global Semantic Norms
Many types of norms can be conceived to quantify
the level of true semantics using the endorsements
given above. For example if |h
i,j
| is a normalized
distance from the center of a state hyper-sphere to
h
i,j
so that |h
i,j
| ≤ 1 and the norm |se(S
i,k
)| gives the
number of states on the current goal path from the
state i to the goal state, then a measure of the
semantics of the current goal path, SM, is:
SM(T
i
)=|h
i,j
| +|se(S
i,k
)|
(8)
SM is a continuous, real valued function that
shows how much of the current goal path has been
completed.
4 CONCLUSIONS
Complex systems such as mobile robots systems, or
distributed industrial control systems need to
communicate and use ontological information about
their environments and about the tasks they perform.
Symbolic operations using formal methods are as yet
prohibitive due to computational reasons while
manual work raises substantially the costs of such
systems. This paper presents a method that combines
ontological operations defined formally with
automatic updates for control ontology based on on-
line direct sensory and actuation data.
REFERENCES
Furst, F., 2008. Ontology Matching with Axioms and
Conceptual Graphs. In IEEE Intelligent Systems. Vol.
23, No. 6, pp. 73-75.
Grantner, J.L., and Fodor, G.A., 2002. Fuzzy Automaton
for Intelligent Hybrid Control Systems. In
Proceedings of the 5-th Hybrid Systems Symposium.
2002, Stanford, USA.
Thamboulidis, K.C., Koumoutsos, G.V., and Doukas,
G.S., 2007. Semantic Web Services in the
Development of Distributed Control and Automation
Systems. In Proceedings of the IEEE International
Conference on Robotics and Automation. April 10-14,
2007, Roma, Italy.
Tomaiuolo, M., Turci, P., Bergenti, F., Poggi, A., 2005. A
Two-Level Approach for Ontology Management in
Multi-Agent Systems. In WETICE 2005, Proceedings
of the 14th IEEE International Workshops on
Enabling Technologies: Infrastructure for
Collaborative Enterprise. June 13-15, 2005, pp. 21-26.
Zimmermann, A., Krötzsch, M., Euzenat, J., and Hitzler,
P., 2006. Formalizing ontology alignment and its
operations with category theory. In FOIS 2006,
Proceedings of the International Conference on
Formal Ontology in Information Systems. November
9-11, 2006, Baltimore, Maryland, USA.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
386
