FUZZY CONTROL FOR CIRCULAR INVERTED PENDULUM

Alan Hood

and Umut Avci

School of Computing and Creative Technologies, University of Abertay Dundee, DD1 1HG, Scotland, U.K.

Deptartment of Software Engineering, Izmir University of Economics, Sakarya Street No:156, Balcova, Izmir, Turkey

Keywords: Inverted pendulum, Fuzzy Control, Non-linear Systems.

Abstract: This paper offers alternative solutions to existing problems in inverted pendulum designs. Three main

problems can be listed as limited track length, hardware complexity and inappropriate control algorithm

usage. Circularly moving cart was proposed to provide unlimited track length. In order to reduce the

hardware complexity, the system was controlled by a microcontroller. Finally, fuzzy control was used for

the control algorithm because of its efficiency, robustness and simplicity. Efficiency of the system is

presented by carrying out experiments on developed inverted pendulum control system.

1 INTRODUCTION

Inverted pendulum, used as a control system

throughout the study, is composed of a rod attached

to a moving cart. Aim of the inverted pendulum is

to stabilize the pendulum vertically by moving the

base whose action is determined by the control

algorithm. One can find different designs for

inverted pendulum in the literature like supported

inverted pendulum (Joldis, 2006), dual inverted

pendulum (Lundberg, Roberge, 2003) or 360 degree

inverted pendulum (Tsai, Lin, 2003).

Main methods used for control can be listed as

PID, genetic algorithms, rule-based learning, neural

networks and fuzzy control (Gupta, Sinha, 1995).

Fuzzy control differentiates from others because it

facilitates the modeling of complex systems as in

real world. In addition to modeling, design and

simulation of these processes can be acquired by

fuzzy logic without using complicated mathematical

models because it uses linguistic variables like in

real world to represent the systems.

(Mirza, Hussain, 1998) developed an inverted

pendulum using PID modes for non-linear systems.

(Wang et al. 2004) proposed a method to balance a

rotary inverted pendulum in the minimum time.

Fuzzy control was used in rotary pendulum

balancing problem by (Yurkovich, Widjaja, 1996).

Swing up and balancing control were applied for

several phases of the process. It was seen that fuzzy

logic provided better solution to control problem

when system constraints were fully determined.

(Ray, Das, Tyagi, 2005) used a similar approach to

balance inverted pendulum moving in a limited

track.

Most of these studies intend only balancing

pendulum without considering all limitations like

lack of memory space, excessive hardware parts

and finite track length. For this reason, this study

focuses on designing an ideal control system with

appropriate control algorithm to overcome the

abovementioned problems. The main objectives of

the study are as follows:

• Building an inverted pendulum system with

minimum hardware configuration.

• Determining the effects of control algorithm on

system control.

• Designing inverted pendulum to provide

unlimited track length.

2 SYSTEM COMPONENTS

In this section, two main parts forming the inverted

pendulum system, control method and hardware,

will be introduced in detail.

2.1 Control Method

Fuzzy controller comprises four main parts: rule-

base, fuzzification, interface mechanism and

defuzzification.

351

Hood A. and Avci U. (2009).

FUZZY CONTROL FOR CIRCULAR INVERTED PENDULUM.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,

pages 351-354

DOI: 10.5220/0002178203510354

 SciTePress

Error, difference between vertical and actual

position of pendulum, has major impact on control.

So, we can assign error as our first input. Change in

error defines how fast pendulum changes its

position, which is another important factor for

control. Then, change in error can be assigned as

second input.

Rules include knowledge of how system works.

Each linguistic variable takes linguistic values that

change from negative large to positive large. Since

we have two inputs and an output it is easy to list all

the rules in a tabular form as follows. One can

create the tabular form for 3 and 7 linguistic values.

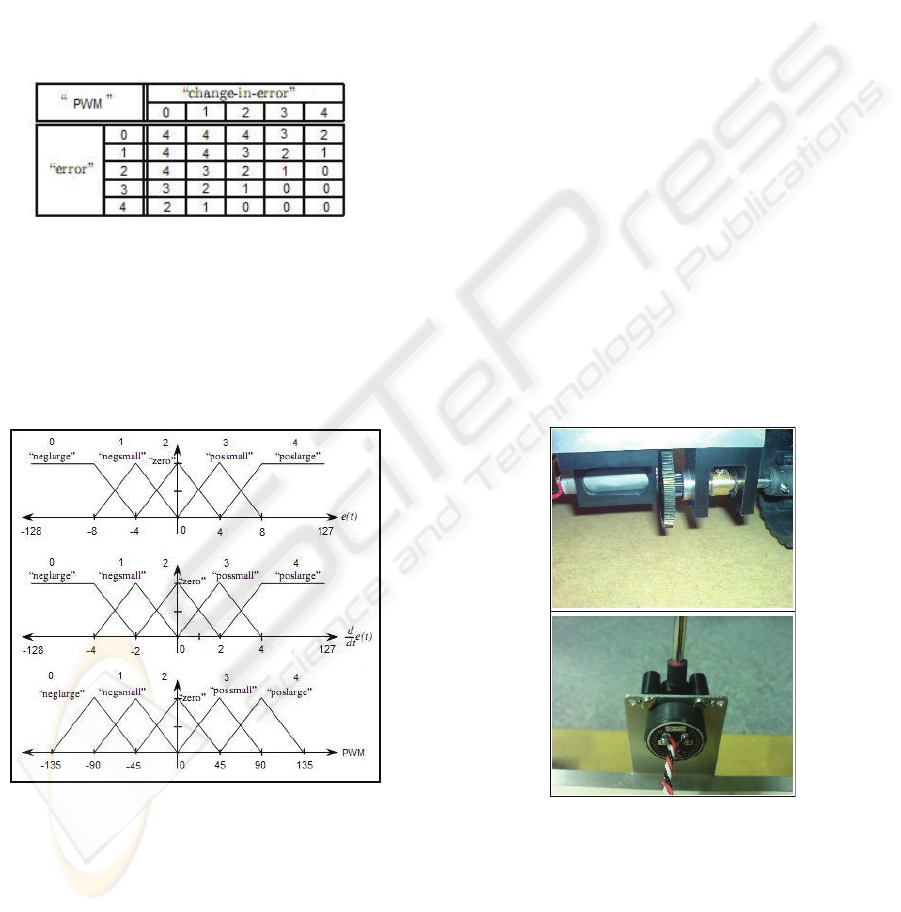
Figure 1: Rule-base with 25 rules.

In Figure 1, body represents the linguistic values

for output (PWM force), left column and top row

represent linguistic values for Error and Change in

Error respectively. Numbers represent the

magnitude of the linguistic values, i.e. “0” for

“neglarge”, “2” for zero and “4” for “poslarge”.

Figure 2: Fuzzy membership functions for 5 linguistic

values.

Mamdani type system was selected for inference

systems where minimum of the active membership

degrees were operated. Center of Gravity (COG)

defuzzification method was used because the

universe of discourse of the output PWM(force)

was continuous. As a result of this calculation, a

crisp output is produced which is the force to be

applied to DC motor at a time.

2.2 Hardware

In this stage, construction of the inverted pendulum

control system will be explained. Input signals will

be obtained from a potentiometer attached to the

pendulum. According to the inputs, the

microcontroller computes the control action and

transfers it to the manipulating element which is a

DC motor in our situation. Basic control operation

can be summarized in a number of steps. The

analog input from the potentiometer must be

converted into a digital word in order to be

processed. The microcontroller inputs these signals

periodically via its internal analog-to-digital

converter and calculates the required output. The

electrical power supplied to motor is determined by

a pulse-width modulated voltage derived using the

Pulse Width Modulation (PWM) peripheral within

the microcontroller. The current available from the

microcontroller is insufficient to drive the motor

directly so an H-bridge motor driver IC must be

used. Since the motor driver system operates at a

higher voltage than the microcontroller and a single

power supply is to be used, a step-down voltage

regulator was employed to power the

microcontroller system.

Figure 3: Geared DC motor (top) and Potentiometer

(bottom).

In order to provide unlimited track length, a

circularly moving inverted pendulum trolley was

designed in the shape of a triangle as shown in

Figure 5. Control board to be attached on pendulum

platform was a 9cm x 9cm stripboard comprising a

40 pin PIC 18F4620 microcontroller, LM7805

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

352

voltage regulator and L6203 H-bridge motor driver.

Using all these parts in such a small space enabled

us achieving minimum hardware object.

Figure 4: Control board.

The control board was used for three main

operations. First, voltage was regulated in order to

be used for different components throughout the

control board. Second, error was read from the pot

and transferred to microcontroller for processing.

And lastly, PWM output produced by

microcontroller was processed in H-bridge for

driving the motor.

Figure 5: Side view of the pendulum trolley.

3 PERFORMANCE

EVALUATION

For performance evaluation, three different fuzzy

controllers defined in previous phase were

embedded into inverted pendulum system one at a

time. Effects of variation in control algorithm were

observed experimentally in terms of system

oscillation, balance angles and steady state.

Number of membership functions and rule base

to be applied should be selected carefully such that

system provides low PWM output for small error

range and high PWM output for large error range.

In the first design, three membership functions for

each inputs and output were defined as well as 9

rules. For this design, system managed to lift the

pendulum up by applying high pulse to motor for

large errors. On the other hand, pendulum could not

be balanced due to high oscillation because control

action produced large PWM output even for small

errors.

Fuzzy inference system with seven membership

functions and 49 rules gave opposite results.

Control output was small enough to balance the

pendulum in very limited error angle. If pendulum

starts to move away from balance limits, motor

power is slowly increased by control action to keep

the pendulum within the boundaries. Nonetheless,

pendulum falls down to extreme edges due to

inadequate acceleration.

Final fuzzy inference system design was

composed of five membership functions and 25

rules. Advantages of the first two systems were

included in the last version that was capable of

balancing pendulum for small angles and lifting it

up for relatively large angles.

Number of Membership

Functions

3 5 7

Lifting up

angle (in degrees)

◌-

◌

◌-

◌

◌-

◌

Oscillation in

terms of angle (in

degrees)

◌-

◌

◌-5

◌ 2

◌-10

◌

Steady

State(S) or Dead-

Band(D)

None

Yes

(S or D)

Yes(S)

Figure 6: Performance comparison in terms of fuzzy

membership functions.

Let us look at the situation where pendulum was

balanced while platform was rotating. Main reason

of this is narrow dead-band which can be defined as

angle range at which pendulum is balanced and

motor stops. For the project, dead-band was

automatically created as narrow based on the

definitions of membership functions. Since dead-

band was small, pendulum was able to stay steady

at the points close to the range. Thus, balance is

achieved while pendulum platform rotates.

Circular movement of pendulum platform is a

FUZZY CONTROL FOR CIRCULAR INVERTED PENDULUM

353

good way for lifting the pendulum up only if

enough acceleration is provided which is dependent

on sudden change of speed. Acceleration rate can be

changed by adjusting sampling time of Error and

Change in Error. Longer sampling time results with

higher alteration rate. Nevertheless, longer sampling

time has negative effects on system control. If one

selects sampling time close or bigger than falling

time, system will not stabilize the pendulum.

Besides, higher sampling time causes oscillation in

the system between the positive and the negative

sides of the vertical because of the magnitude of the

PWM output. To solve this dilemma, appropriate

sampling time must be selected. During inverted

pendulum development process, several artificial

sampling times (30 ms, 60 ms, 125 ms, 250 ms and

500 ms) were created using delay function. Test

results indicated that oscillation decreases for

smaller sampling times. That’s why, for inverted

pendulum system the fastest internal oscillator

option was employed without any delay function to

provide the shortest calculation interval possible.

4 CONCLUSIONS

In this paper, we focus on developing an inverted

pendulum with the aim of minimizing the size and

the cost of the system structure while increasing the

reliability and performance. By using a

microcontroller, hardware requirements are greatly

reduced as well as total cost. A new approach to

inverted pendulum design is proposed so that

unlimited circular movement is assured. Fuzzy

inference system with five triangular membership

functions and 25 rules provide an appropriate way

of control as far as low memory capacity of the

microcontroller is concerned. Empirical results

show that pendulum is balanced vertically either in

steady-state or in dead-band.

Inverted pendulum control system can be

improved in a number of ways. Lifting the

pendulum up from extreme edges can be achieved

by replacing the current pendulum with a lighter

and/or shorter one. A mass can be added at the top

of the pendulum in order to provide steady

movement and to facilitate the stabilization but such

a modification changes the place of center of

gravity to a great extent. Type of the motor and size

of the wheels affect the acceleration. Motor can be

changed with a powerful one or/and size of the

wheels can be bigger to provide more speed and

acceleration correspondingly.

It is known that oscillation can be reduced by

decreasing sampling time. Lower sampling time can

be achieved by using higher processor speeds. In

the project, sampling time was determined by the 8

MHz internal oscillator. So, a crystal oscillator may

be added to system as external clock source. Such a

modification increases the processor speed from 8

MHz up to 40 MHz.

REFERENCES

Gupta, M. M., Sinha N. K. 1995. Intelligent Control

Systems. New Jersey. IEEE Press.

Joldis, A. 2006. Supported inverted pendulum, another

kind of inverted pendulum. IEEE International

Conference on Automation, Quality and Testing,

Robotics. Vol. 1. pp. 143-148.

Lundberg, K. H., Roberge, J. K. 2003. Classical dual-

inverted-pendulum control. Proceedings. 42nd IEEE

Conference on Decision and Control. Vol. 5. pp.

4399 - 4404.

Mirza, A., Hussain, S. 1998. Robust controller for

nonlinear and unstable systems: inverted pendulum.

Journal of AMSE. Vol. 55. No. 3,4.

Ray, G., Das, S. K., Tyagi, B., 2005. Stabilization of

Inverted Pendulum via Fuzzy Control, IE(I) Journal–

EL.

Tsai, F. K., Lin, J.S. 2003. Backstepping Control Design

of 360-Degree Inverted Pendulum Systems.

Automatic Control Conference. pp. 138 – 143.

Wang, Z., Chen, Y., Fang, N., 2004. Minimum-time

swing-up of a rotary inverted pendulum by iterative

impulsive control. Proceedings of the 2004 American

Control Conference. Vol. 2. pp. 1335 – 1340.

Yurkovich, S., Widjaja, M., 1996. Fuzzy controller

synthesis for an inverted pendulum system. Control

Engineering Practice. Vol. 4. Issue 4. pp. 455-469.

Microchip PIC18F4620 Data Sheet. [online].

Available from:

http://ww1.microchip.com/downloads/en/DeviceDoc/396

26e.pdf

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

354