A LOSSLESS IMAGE COMPRESSION METHOD WITH THE

REVERSIBLE DATA EMBEDDING CAPACITY

Ju-Yuan Hsiao and Zhi-Yu Xu

Department of Computer Science and Information Engineering, National Changhua University of Education

Changhua, Taiwan 500, R.O.C.

Keywords: Reversible data embedding, Lossless image compression, Image processing.

Abstract: The current reversible data embedding techniques can be divided into 2 categories: those developed by the

untreated original images and those developed by the images treated via the lossy compression as the

reversible target. So far, there has not been any literature discussing the issue of the reversible data

embedding action finished during the lossless still image compression. Our method employs Chuang and

Lin’s simplified lossless image compression method to develop a reversible data embedding technique. Our

method successfully embeds the secret data in the lossless image compression codes and have the secret

data reversed to the original image as the secret data are retrieved wherefrom. According to the

experimental results, the proposed method performs well on the embedding capacity and compression

effects.

1 INTRODUCTION

An effective way to safely transmit secret data to the

receiver by Internet is to embed the secret data into

the digital media such as image and then transmit the

embedded media. This technique is called the

information hiding technique. If the embedded

media reverse to the original media after the secret

data are retrieved, it is called the reversible data

embedding technique, otherwise, it is called the

irreversible data embedding technique. The

proposed technique is the reversible data embedding

technique using still grayscale images as the media.

In the recent decade, there are many studies

relating to the reversible data embedding techniques.

There are 2 major categories under the properties of

the media. One is the untreated original images

(Alattar, 2004; Celik et al, 2005; Chang & Lu,

2006A; Ni et al, 2006; Thodi & Rodriguez, 2007;

Tain, 2003) and another is the encoded images

treated by the lossy compression(Chang & Lu,

2006B; Chang & Lin, 2006; Chang & Lin, 2007;

Chang, Hsieh & Lin, 2007; Chang, Wu & Hu, 2007).

Nevertheless, some application domains such as the

medical images, military mapping images and digital

artistic works employ the lossless compression

techniques to guarantee the exact precision of the

image quality for the image storage and

transmission. Therefore, it is a key issue to discover

the reversible data embedding technique able to add

extra data to the images treated by the lossless

compression techniques. This paper employs the

images treated by Chuang and Lin′s (Chuang & Lin,

1998) simplified lossless image compression

technique as the subject to develop a reversible data

embedding technique able to successfully embed the

secret data in the lossless image compression codes

and have the embedded image reversed to the

original image as the secret data are retrieved

wherefrom. According to the experimental results,

the proposed technique performs well on the

embedding capacity and compression effects.

The rest of this paper is organized as follows.

Section 2 introduces Chuang and Lin’s (Chuang &

Lin, 1998) lossless compression method. In Section

3, our method is described. The experimental results

are presented and discussed in Section 4. Finally, the

conclusions are provided in Section 5.

2 CHUANG AND LIN’S (1998)

METHOD

2.1 Compression

In this section, the lossless compression technique

Hsiao J. and Xu Z. (2009).

A LOSSLESS IMAGE COMPRESSION METHOD WITH THE REVERSIBLE DATA EMBEDDING CAPACITY.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 27-32

DOI: 10.5220/0002181100270032

 SciTePress

proposed by Chuang and Lin for grayscale images is

simply illustrated. First, the original grayscale image

is divided into n×n blocks of which each is treated

by the lossless compression from left to right and up

to down individually. Since Chuang and Lin have

proved that the 3×3 block leads to the optimal

compression effect, the illustration of 3×3 block is as

below. The individual 3×3 block is treated by the

following steps.

Given a 3×3 block as the subimage A of which 9

pixel values are

810

,...,, ggg

, see Figure 1.

Figure 1: Block A.

Find the minimum

8i0

≤≤

min

and the base

1ggb

8i0

+−=

≤≤

)minmax(

in the block.

Then compute

80,1,2,...,,' =

−

= imgg

. Let

′

denote

)',...,','(

810

ggg

.We obtain

1max0min −==

≤≤

bg',g'

8i0

, so nine-dimensional vector

)',...,','(

810

ggg

can be treated as a nine-digit

number

ggg )'...''(

810

in the base-b number system.

For convenience, let

33×

be the collection of all 3×3

subimage

′

, and the base-set B = {1, 2, 3,…,

256}. Afterwards, define a function

BVf ×=

×33

→{non-negative integers}

),'( bAf

= the decimal integer equivalent to the

base-b number

ggg )'...''(

810

∑

×=

0678

'...))')''((...( gbbgbgbg

×+×+×+×=

⎡⎤

log

Z =

represents the number of bits required

by the binary transformation of

),A'( bf

As to achieve the optimal compression effect,

according to the b-value, there are 3 encoding cases:

Case (1): 1≦b≦11, the encoding as:

[ c=0 (1 bit) , b (7 bits) , m (8 bits) , f (Z

bits) ]

Case (2): 12≦b≦127, the encoding as :

[ c =0 (1 bit), b (7 bits), m (8 bits), P(min,max)

(7 bits), f (Z

bits)]

P(min,max) is used to record the locations of

minimum (min) and maximum (max) values of

;

therefore, there are 9×8=72 combinations. We need

7 bits to record all situations. The computation of

P(min, max) is as follows :

Case 1 : if max<min then

P(min,max)=min*8+max+1 (1)

Case 2 : if max>min then

P(min,max)=min*8+max (2)

Since the minimum and the maximum of

is 0

and b-1, recording P(min,max) equals to record 2

pixel values of

. Therefore, when computing

),'( bAf

, we only need record the residual 7 pixel

values. Consequently, in this case, it is

⎡⎤

log

bits rather than

⎡⎤

log

Z =

Case (3): 128≦b≦256, the encoding as:

[ c =1(1 bit), the 9 pixel values of the original

block (9×8 bits) ]

Following the preceding techniques, the first bit

value (c) of the compression codes of each block

indicates that the following bits are either the

original 9 pixel values or the compression codes.

The lossless compression technique proposed

by Chuang and Lin employs the relation between c

and b values to neglect c and further compress the

remaining information. However, this paper employs

merely the individual block compression technique

of Chuang and Lin and introduces the reversible data

embedding technique; therefore, the further

compression part of Chuang and Lin’s method is

excluded here. Please see (Chuang & Lin, 1998) for

the further detail inofrmation.

2.2 Decompression

In the decoding procedures, first check the first bit c.

Suppose c=1, then take the next 72 bits to derive the

original 9 pixel values in the block; suppose c=0,

then take the next 7 bits to obtain the b value. There

are 2 cases under the b values.

Case 1: 1≦b≦11

We obtain the values of m and f by taking the

next 8 and

⎡⎤

log

bits, respectively. Then

represent the decimal integer f as a nine-digit base-b

number

ggg )'...''(

810

. According to

}'{

=ii

and

m values, we can derive the original 9 pixel values in

the block.

Case 2: 12≦b≦127

We obtain the values of m, P(min,max) and f by

taking the next 8, 7 and

⎡⎤

log

Z =

bits

respectively. Through the value of P(min,max) and

Eq.s (1) and (2) we know the positions of the

minimum and maximum in the block with the values

0 and b-1. Then represent the decimal integer f as a

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications

seven-digit base-b number to obtain the residual 7

values. According to

}'{

=ii

and m values, we can

derive the original 9 pixel values in the block.

3 THE PROPOSED METHOD

In the following section, we describe how to develop

a reversible data embedding technique applicable to

the simplified Chuang and Lin′s lossless

compression method. Our method embeds secret

data in non-overlap blocks one by one. Our sequence

is from right to left and from bottom to top. It is the

backward sequence of Chuang and Lin′s method.

3.1 One Bit Embedding Method

The image is segmented into 3×3 blocks and each

block thereof is encoded by the simplified Chuang

and Lin′s method. For each block′s compressed code,

we execute the following 1 data bit embedding steps.

Step 1. If the value c of the block′s compressed code

to be treated is 1, there is no data

embedding; if c is 0, then the residual codes

(b + m+ f or b +m +P(min,max)+ f) are

processed by Step 2.

Step 2. If the data bit to be embedded is 0 (1), the

designed X

) is selected to XOR the

residual code. The result of the XOR

operation is the data embedded block′s final

compression code.

Step 3. Verify whether the embedded data can be

retrieved accurately in the process of

retrieving. If it succeeds, we accomplish the

data embedding process; if it fails, we

cannot embed data in this block and Case

(3) (c = 1) of Chuang and Lin’s technique is

used to encode this block.

The preceding algorithm mentions that it is

necessary to verify whether the correct retrieval of

the embedded data in the process of retrieving them

occurs. The main reason is that we fail to know

whether the code is 1 or 0 embedded in the

retrieving stage; therefore, we must XOR the data

embedded compression code with X

and X

as to

obtain the 2 reversed codes and judge which one is

the true embedded bit and the original compression

codes. If the judgment conditions employed can

exclude accurately the non-original compression

codes and reverse the contents of the original block

and obtain the embedded data, we embed data;

otherwise, we do not embed data therein. The

following is the conditions employed to exclude the

inaccurate compression codes of the block:

(1) The first judgment condition is that using the

values of b, m, P(min,max) and Z

to decode all

pixel values of the block must be within 0-255,

so those rather than the preceding values are

definitely not the original compression codes.

(2) If the result fails to be obtained by the first

condition, the coincidence of the contents of the

adjacent known blocks and the pixel values of

the tested block are used to judge which one is

the original block. Except for few blocks which

the edges pass through, the true original blocks

share the high similarity with the adjacent blocks.

Therefore, we select the tested block with the

highest coincidence with the adjacent known

blocks as our final result. We employ the

side-matching idea to judge the coincidence of

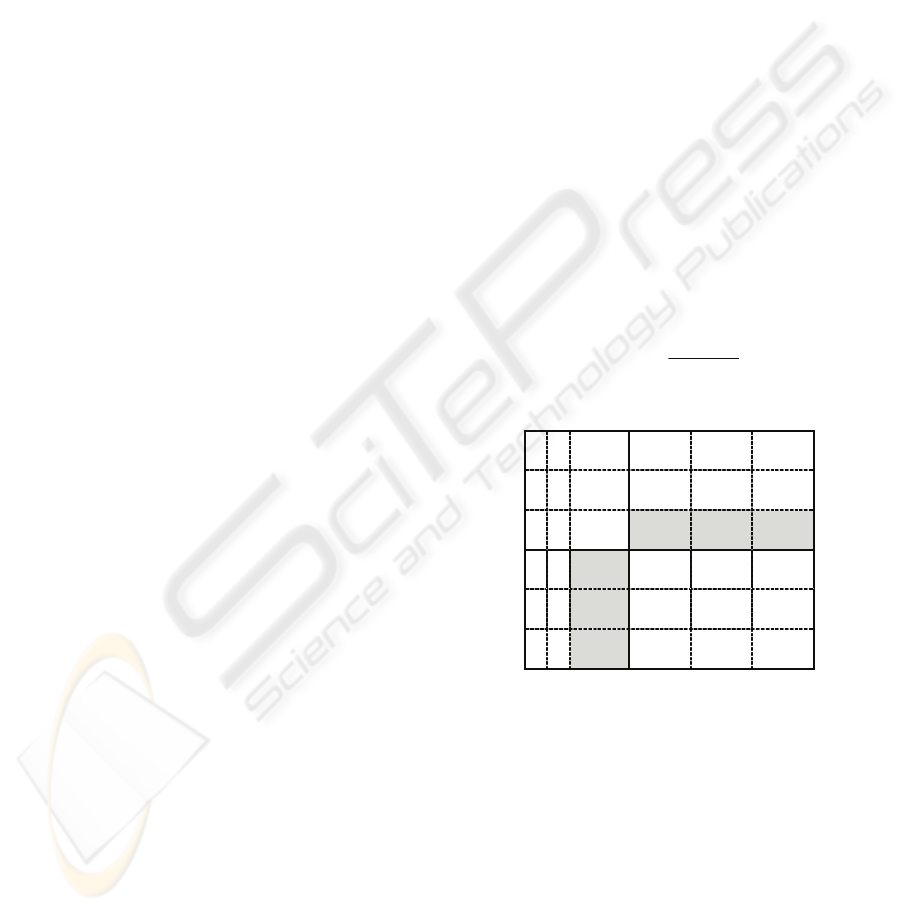
the tested and adjacent known blocks. See Figure

2. X is the block to be tested and X

, X

and X

are the pixel values of X. U and L are

respectively the upper and left known adjacent

blocks of X. U

, U

and L

, L

are

respectively the pixel values of U and L. Eq. (3)

is used to measure the coincidence of X and U&L.

The smaller value of DIS(X,U,L) indicates the

higher coincidence of X and U&L.

3212

1331

)())

((),,(DIS UX

XLUX −+

−=

3331

2321

3313

)()()( LXLXUX −+−+−+

(3)

Figure 2: Side-Match schematic.

3.2 One Bit Extraction Method

As we retrieve the embedded data and obtain the

original image by decoding, the block processing

sequence is from left to right and up to down which

is opposite to that of data embedding.

First, the first bit c of compression code of each

block is checked. If c = 1, it denotes that there is no

data embedding and the following 8*9 = 72 bits

represent the original 9 pixel values; therefore, it is

applicable to reverse the block directly. If c = 0, it

denotes that there is data embedding. Therefore, we

A LOSSLESS IMAGE COMPRESSION METHOD WITH THE REVERSIBLE DATA EMBEDDING CAPACITY

take the following 72 bits to XOR with X

and X

obtain 2 compression codes to be tested. Afterwards,

we obtain the accurate length of the test codes and

judge which is the true original codes in accordance

with the verification conditions prescribed in Section

3.1. Since we have confirmed that the accuracy of

the retrieved original codes in the process of

retrieving data as embedding data, we can obtain the

original compression code and get the embedded

data without any problem. As we verify the

embedded data as 0 or 1, we can obtain the original

9 pixel values by decoding the original codes with

the decoding method proposed by Chuang and Lin.

3.3 XOR Patterns Design

In the proposed technique, XOR patterns X

and X

are used to be the media of data embedding.

Apparently, the design of XOR patterns impacts the

information quantity embedded in the image. A

good designed XOR pattern decreases the

opportunity of data cannot be embedded in blocks

and advanced the whole information embedding

capacity accordingly.

Through the experiments, we obtain the

regularity of the XOR patterns design. The designed

XOR patterns are able to reduce the opportunity of

misjudgment during the retrieval of embedded data,

which leads to the reduced inapplicability of data

embedding. The longest length of codes is 72 bits, so

the length of XOR patterns is all 72 bits.

If there is 1 data bit embedded in a block, it

demands only 2 XOR patterns X

and X

. The

design manner is the different 8

bit and all other

bits are 0 in X

and X

. See Figure 3. Such a design

results from that the 8

bit of X

or X

indicates the

first bit of m part of the compressed codes;

accordingly, in the reversing process of original

pixel values of the block, the difference between the

pixel values of the true original block and the other

block at the relative position is 128. At this rate, the

pixel values of the other block may not be within

0-255. Even though aforesaid values are within

0-255, there is a huge difference between the

aforesaid block and its adjacent block, leading to the

judgment of non-original block. Consequently, most

blocks are verified to be applicable to data

embedding in the data embedding stage as to

increase the embedding capacity.

If there are 2 data bits to be embedded in each

block, it demands 4 XOR patterns as X

, X

and

. We let the 8

and 9

bits differ of

X,...,X

with the values of 00, 01, 10 and 11. If there are 3

data bits to be embedded in each block, it demands 8

XOR patterns as X

,…,X

. At this time, in addition

to the different 8

and 9

bits, we employ the

alteration of the first bit because it is the first bit

responding to part b of the compressed codes. For

this reason, there is a difference of 64 of the base

values in the process of retrieving data and reversing

the original values of the block, leading to the values

out of 0-255. Even though the values are within

0-255, there is a huge difference between the

aforesaid block and its adjacent block, leading to the

judgment of non-original block.

If there are 4 data bits to be embedded in each

block, the XOR patterns are similar to those

embedding 3 data bits. The alteration of the 1

, 2

and 9

bits is used to construct X

,…,X

. If there

are 5 data bits to be embedded in each block, it

demands the alteration of the 1

, 2

, 8

, 9

and 16

bits to construct X

,…,X

. If there are 6 data bits or

more to be embedded in each block, it extends the

case of 5 data bits embedding. That is, the alteration

of the 1

, 2

, 8

, 9

and 16

bits plus 17

and 18

bits to construct the required XOR patterns.

Figure 3: XOR patterns design schematic.

3.4 Multi-bits Embedding and

Extracting

In this Section, we describe how to extend the

technique of embedding and extracting 1 data bit in

a block prescribed in Subsections 3.1 and 3.2 to the

multi-bits embedding and extracting.

If there are multi-bits to be embedded in a block,

the modification of Step 2 of the embedding method

mentioned in Subsection 3.1 is needed. The steps of

embedding n data bits in a block are as follows.

Step 1. If the value c of the block′s compressed code

to be treated is 1, there is no data

embedding; if c is 0, then the residual codes

(b + m+ f or b +m +P(min,max)+ f) are

processed by Step 2.

Step 2. If the decimal value of the n-digit to be

embedded is i,0≤i≤2

-1, the designed X

selected to XOR the residual code.

The result of the XOR operation is the data

embedded block′s final compression code.

Step 3. Verify whether the embedded data can be

retrieved accurately in the process of

extraction. If it succeeds, we accomplish

the data embedding process; if it fails, we

b(7 bits ) m(8 bits)

P(min,max) + Z

or Z

(57 bits )

0000000

00000000 0000…0000

10000000

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications

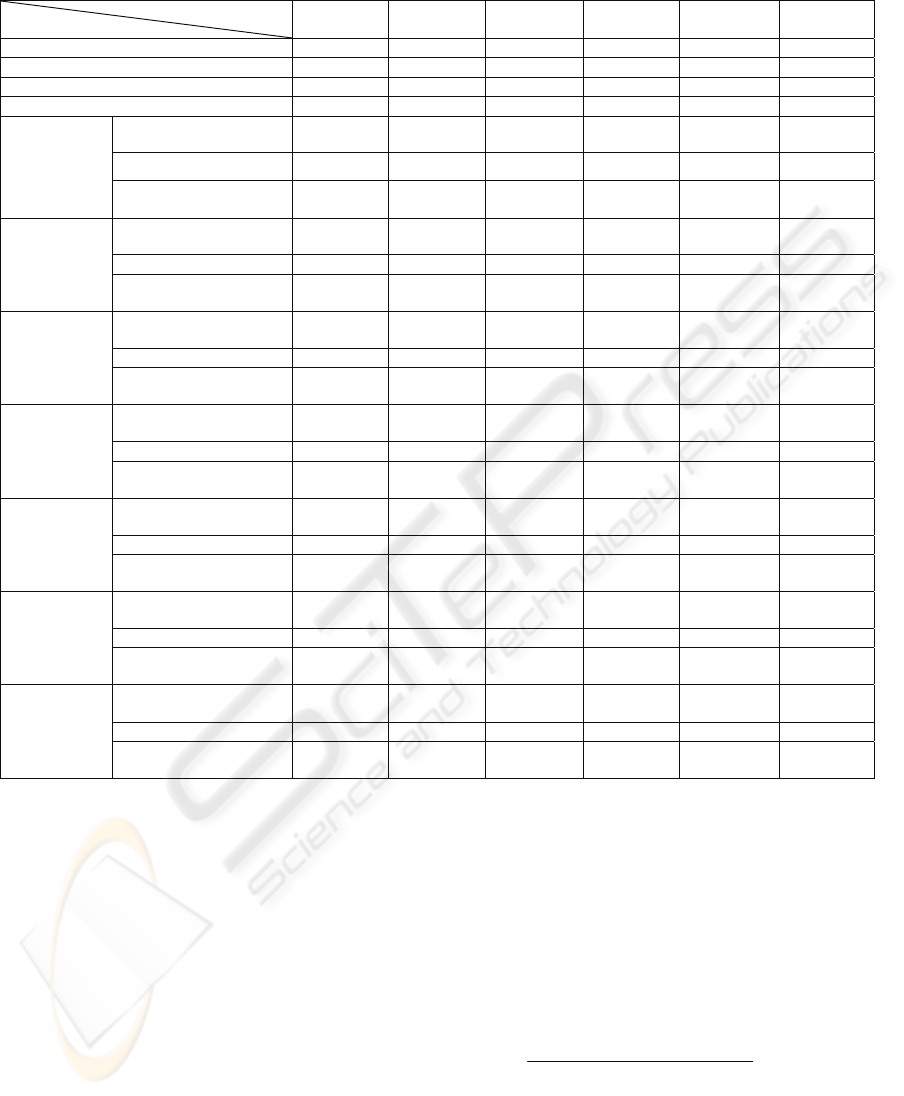
Table 1: Various image sizes and embedding capacities.

Images

Attributes

Lena Baboon Pepper Gold Girl F-16

Original image sizes (bits) 2080800 2080800 2080800 2080800 2080800 2080800

Lossless compressed image sizes 1381455 1727667 1384059 1488330 1419340 1317704

Number of blocks 28900 28900 28900 28900 28900 28900

Number of Case 3 blocks 107 438 123 6 101 96

Embed 1 data

bit / block

Embedded image sizes

(bits)

1381455 1727845 1392649 1488330 1419340 1317704

Capacity (bits)

28793 28449 28496 28894 28799 28804

Number of increasing Case

3 blocks

0 13 281 0 0 0

Embed 2 data

bits / block

Embedded image sizes

(bits)

1382051 1734385 1393686 1488881 1419607 1319353

Capacity (bits)

57456 55158 56806 57694 57550 57294

Number of increasing Case

3 blocks

65 883 374 47 24 157

Embed 3 data

bits / block

Embedded image sizes

(bits)

1384519 1746568 1395980 1491868 1421035 1322316

Capacity (bits) 85404 75813 84594 85872 85983 84975

Number of increasing Case

3 blocks

325 3191 579 270 138 479

Embed 4 data

bits / block

Embedded image sizes

(bits)

1391521 1775092 1401160 1502622 1427535 1328509

Capacity (bits) 115172 87884 111204 111460 113000 111140

Number of increasing Case

3 blocks

942 6491 976 1029 549 1019

Embed 5 data

bits / block

Embedded image sizes

(bits)

1397969 1786960 1410254 1516953 1435959 1333804

Capacity (bits) 137545 105995 143885 135535 139245 137525

Number of increasing Case

3 blocks

1284 7263 1382 1787 950 1299

Embed 6 data

bits / block

Embedded image sizes

(bits)

1416517 1832164 1433781 1560736 1457216 1350418

Capacity (bits) 159228 108600 157530 148872 160698 159600

Number of increasing Case

3 blocks

2255 10362 2522 4082 2016 2204

Embed 7 data

bits / block

Embedded image sizes

(bits)

1443427 1885390 1467086 1620516 1487441 1386402

Capacity (bits) 175490 100065 172130 150780 176449 169008

Number of increasing Case

locks

3723 14167 4187 7354 3592 4660

cannot embed data in this block and Case

(3) (c = 1) of Chuang and Lin’s technique is

used to encode this block.

The verification method of the accuracy of

the data retrieval in the process of

retrieving them is identical with that

mentioned in 3.1, so there is no more

repeated illustration.

4 EXPERIMENTAL RESULTS

As far as we know, this is the unprecedented paper

that employs the reversible data embedding

technique to the lossless compression. Hence, the

experimental emphasis is the inquiry on the

alteration of embedding quantity of the diverse

images and the impact of the data embedding

quantity on the compression ratio.

Six 512 × 512 sized grayscale images are used to

conduct the experiments for verifying the effect of

the proposed technique. The 6 images are Lena,

Baboon, Pepper, Gold, Girl and F-16.

The compression ratio is used to assess the entire

compression effect. See Eq. (4).

%100×=

sizefileOriginal

ncompressioaftersizeFile

(4)

The experimental data of the embedding capacity

are shown in Tables 1.

The experimental results in Table 1 indicate that

there is a significant difference of the embedding

capacity between Baboon and other images. The

A LOSSLESS IMAGE COMPRESSION METHOD WITH THE REVERSIBLE DATA EMBEDDING CAPACITY

main reason is Baboon is a complex image.

Therefore, there are more blocks unable to be

encoded by the lossless compression (blocks in Case

3) . Thus, we can not embed data therein. Likewise,

even the block can be compressed, there are more

blocks where the data unable to be retrieved

successfully so that we fail to embed data therein.

As a result, the entire embedding quantity is

relatively less.

As for the performance of the compression ratio,

when there is only 1 data bit embedded in each

block, except for the slight advancement of Baboon

and Pepper, the compression ratio of other images

are identical with that of the original compression

ratios. That is, the codes remain the same after we

embed data. As the embedding capacity increases,

the codes expand slowly as well. However, the

speed of the expansibility of the codes is much

slower than that of the increased data embedding

quantity. Except for the case that there are 7 data bits

embedded in the blocks of Baboon. What is

worthwhile mention is that the compression ratio of

other images before and after data embedding differs

within 1% except for that of Baboon when there are

less than 5 data bits embedded in each block. Based

on the result, it proves that the designed XOR

patterns perform well on the advanced embedding

capacity.

To sum up, we successfully propose a new

technique adding the reversible data embedding to

the lossless compression. The proposed technique

performs well in the smooth images whereas it fails

to function well on the complex images concerning

the information embedding quantity and the

expansibility of compression codes.

5 CONCLUSIONS

This paper employs the simplified Chuang and Lin′s

method to develop a reversible data embedding

technique applicable to the lossless compression

technique. According to the experimental results,

such a technique performs well on the information

embedding quantity and expansibility of

compression codes. As far as we know, this is the

unprecedented paper that employs the reversible

data embedding technique to the lossless

compression. We will dedicate ourselves to the

reduced compression ratio and the advanced

embedded information quantity and the further

research of other reversible data embedding

techniques of lossless compression techniques.

ACKNOWLEDGEMENTS

This work was supported in part by National Science

Council of Taiwan, R.O.C. under Grant no. NSC

97-2221-E-018-023.

REFERENCES

Alattar, A.M., 2004. Reversible watermark using the

difference expansion of a generalized integer

transform. IEEE Transactions on Image Processing

13(8), pp.1147-1156.

Celik, M.U., Sharma, G., Tekalp, A.M., Saber, E., 2005.

Lossless Generalized-LSB data embedding. IEEE

Transactions on Image Processing 14(2), pp.253-266.

Chang, C.C., Hsieh, Y.P., Lin, C.Y., 2007. Lossless data

embedding with high embedding capacity based on

declustering for VQ-compressed codes, IEEE

Transactions on information forensics and security,

2(3), pp.341-349.

Chang, C.C., Lin, C.Y., 2006. Reversible Steganography

for VQ-Compressed Images Using Side Matching and

Relocation, IEEE Transactions on Information

Forensics and Security, 1(4), pp.493-501.

Chang, C.C., Lin, C.Y., 2007. Reversible steganographic

method using SMVQ approach based on declustering,

Information Sciences, 177(8), pp.1796-1805.

Chang, C.C., Lu, T.C., 2006A. A difference expansion

oriented data hiding scheme for restoring the original

host images. The Journal of Systems and Software

Vol. 79, pp.1754-1766.

Chang, C.C., Lu, T.C., 2006B. Reversible index-domain

information hiding scheme based on side-match vector

quantization, The Journal of Systems and Software,

79(8), pp.1120-1129.

Chang, C.C., Wu, W.C., Hu, Y.C., 2007. Lossless

recovery of a VQ index table with embedded secret

data’, Journal of Visual Communication and Image

Representation, 18(3), pp.207-216.

Chuang, T.J., Lin, J.C., 1998. A New Algorithm For

Lossless Still Image compression, Pattern

Recognition, 31(9), pp.1343-1352.

Ni, Z., Shi,Y.Q., Ansari, N., Su, W., 2006. Reversible

Data Hiding. IEEE Transactions on Circuits and

systems for video technology 16(3), pp.354-362.

Thodi, D.M., Rodriguez, J.J., 2007. Expansion embedding

techniques for reversible watermarking. IEEE

Transactions on Image Processing 16(3), 721-730.

Tian, J., 2003. Reversible data embedding using a

difference expansion, IEEE Transactions on Circuits

and Systems for Video Technology 13(8), pp.890-896.

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications