
PROVIDING SPATIAL INTEGRITY FOR DISTRIBUTED
UNMANNED SYSTEMS
Peter Simon Sapaty
Institute of Mathematical Machines and Systems, National Academy of Sciences, Glushkova Ave 42, 03187 Kiev, Ukraine
Keywords: Unmanned systems, Distributed scenario language, Networked interpretation, System integrity, robotic
swarms, Reconnaissance, Camp security, Convoys, Explosive ordnance disposal, Gestalt, World super-
machine.
Abstract: Due to the increased complexity of tasks delegated to unmanned systems, their collective use is becoming of
paramount importance for performing any reasonable jobs. An approach is offered where group behaviors
are accomplished automatically rather than set up manually, as usual. Missions in the Distributed Scenario
Language (DSL) can be executed jointly by communicating interpreters in system units. Scenarios like
reconnaissance, camp security, convoy, mule, and explosive ordnance disposal in DSL, oriented on different
numbers of cooperating units, are demonstrated. The approach allows us to effectively manage any teams,
from human to robotic, and from homogeneous to heterogeneous, regardless of the number of components
in them. A variety of other applications of the technology are outlined too, already researched or prospective,
also its relation to the gestalt philosophy, where super-summative whole dominates over system parts,
defining their sense and even existence, rather than vice versa. The paradigm discussed may also represent a
distributed dynamic world super-machine operating in parallel with both information and physical matter.
1 INTRODUCTION
With the world dynamics increasing due to global
warming, numerous natural and manmade disasters,
military conflicts, and international terrorism, using
unmanned (ground, sea, underwater, and air)
systems can alleviate many problems and save lives
in hazardous environments. Because of the
complexity of tasks delegated to unmanned solutions
and still insufficient capabilities of existing robotic
vehicles, their simultaneous, collective use may be
of paramount importance to perform any reasonable
jobs. Operating together, the unmanned groups,
often called swarms, can fulfill the required
objectives despite possible runtime damages to
individual units.
We are offering a novel approach to organization
of unmanned systems, oriented from the very
beginning on parallel solutions in physical spaces,
with swarm behaviors resulting naturally and
accomplished automatically, rather than
programmed manually. This approach, symbolically
called “overoperability” from the previous
publications (Sapaty, 2002, 2005), allows us to
create, modify, analyze, process, and manage any
distributed systems, establishing local and global
dominance over them.
Within the overoperability philosophy, an
integral mission scenario, written in a special high-
level scenario language (Sapaty, 1999, 2005) and
reflecting semantics of what to be done in a
distributed space rather than details of
implementation, is executed in a parallel and
cooperative manner by dynamically networked
unmanned units. During the scenario evolution, any
operations can be accomplished in the world, along
with the needed movement of code, equipment and
“doers” (both artificial and biological), as well as
creation and maintenance of physical and virtual
infrastructures supporting the missions.
This paper is essentially inspired by the
European Land Robotic Trial (M-ELROB, 2008) in
which the author participated. It was conducted to
provide trials as close as possible to operational
scenarios for UGVs/UAVs with focus on short-term
realizable robot systems. The day and night trials
were organized within the following five main
scenarios: non-urban reconnaissance, camp security,
transport convoy, transport mule, and explosive
ordnance disposal. Only a limited number of robotic
units were engaged in every scenario, just one or
29
Sapaty P. (2009).
PROVIDING SPATIAL INTEGRITY FOR DISTRIBUTED UNMANNED SYSTEMS.
In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Intelligent Control Systems and Optimization,
pages 29-40
DOI: 10.5220/0002181200290040
Copyright
c
SciTePress

two, whereas every scenario could potentially be
executed with much higher efficiency if using
robotic teams with many units, which cooperate with
each other.
The paper also reflects activity on the project
started under the sponsorship of Alexander von
Humboldt Foundation (AvH) in Germany. One of its
aims is formalization of known mission scenarios in
such a way that they could be performed by any
available numbers of robotic vehicles, with the
management burden effectively shifted to self-
organized robotic teams -- thus relieving human
operators from traditional routines and allowing
them concentrate on mission goals and global
efficiency instead.
2 DISTRIBUTED SCENARIO
LANGUAGE (DSL)
The approach described here is based on the
Distributed Scenario Language (DSL), which allows
us to set what to do in a distributed world on a
semantic level, abstracting from details of how to do
this and with which resources, delegating these to
the intelligent automatic interpretation. Being a
universal programming language with advanced
parallel and distributed capabilities, DSL can also
describe tasks and behaviors on any levels, if
needed. The language can be used by humans who
should follow its instructions individually or
collectively, or can be directly executed by robots
and their teams. Any mixed human-robotic
organizations can be managed in DSL too.
2.1 The World
The world DSL operates with can be virtual,
physical, or combined.
Virtual World (VW) is discrete and consists of
nodes and links connecting these nodes. Any
information can be associated with both nodes
and links in the form of their names (contents).
Nodes have unique addresses in VW, whereas
their names (same as names of links) may repeat
throughout the VW. Nodes can be accessed
directly, globally, by their names or addresses, or
locally, from each other, via the (named) links,
whereas links can be accessed only locally--from
the adjacent nodes. A variety of broadcasting
possibilities are available in the VW, both in a
global and local way, for example, from outside
to all nodes, from a node directly to all other
nodes, or from a node to all neighboring nodes
via the selected or all adjacent links.
Physical World (PW) is continuous. Any point in
it can be identified and accessed by the
coordinates expressed in a certain coordinate
system, also with certain precision. Staying in a
PW point, you can lift local physical parameters
from the world and, possibly, also change them,
impacting the world locally too.
Virtual-Physical World (VPW) is the one where
VW nodes additionally associate with certain
coordinates in the PW. VPW is discrete on a
snapshot, but the nodes can change their physical
coordinates overtime. The VPW nodes can be
globally accessed by their names, addresses, or
physical coordinates (for the latter, more
correctly: by coordinates of the expected center
and a radius of the region, due to limited
precision of the coordinates). Also locally, via
links--same as for the pure VW. In addition to
the broadcasting capabilities of VW, nodes in
VPW can also be massively accessed/entered by
identifying a probable region in PW where they
are expected to exist--by the region’s center and
a range (radius) from this center, where the latter
may be of any value.
2.2 High-Level Scenarios
The world, as described above, is navigated and
processed in a parallel and distributed way by high-
level DSL scenarios having the following main
features.
General Features:
A DSL scenario (or program, in a conventional
notation) describes development of activities in a
distributed world as parallel transitions between
sets of progress points, or props.
Starting from a prop, a program action may
result in one or more new props, or remain in the
same prop.
Each prop has a resultant value and a resultant
state.
Different actions (whatever complex they might
be), starting from the same prop, may evolve
independently or interdependently, and
sequentially or in parallel, each contributing to
the resultant set of props on this group of actions.
Actions may also succeed each other in the space
of props, with new actions applied in parallel
from all props reached by the previous actions,
resulting altogether in the integrated set of props
on all these applications.
Elementary operations can be defined on the
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
30

values of props reached by other actions (the
latter of any complexity), leading to the resultant
prop with associated value (which may be
multiple) and resultant state.
The scenarios can form new or remove existing
nodes and links in the distributed VW or VPW,
allowing us to create, modify, and process any
graph-based infrastructures in these worlds.
Association with World Nodes/Points:
Any prop can be associated with a node in VW
or a position in PW, or both, like in the case of
VPW.
A prop can also be linked separately with VW
nodes and PW positions, allowing us to operate
with the two worlds independently.
Any number of props can be associated
simultaneously with same points of the worlds.
Staying with nodes/positions in the worlds, a
prop allows us to directly access local data in
these points, both virtual (information) and
physical (matter).
Different Types of Variables:
Heritable variables – these are starting in a prop
and serving all subsequent props, which can
share them in both read & write operations.
Frontal Variables – are an individual and
exclusive prop’s property (not shared with other
props), being transferred between the
consecutive props, and replicated if from a single
prop a number of props emerge.
Environmental Variables – are accessing
different elements of physical and virtual words
when navigating them, also a variety of
parameters of the internal world of DSL
interpreter.
Nodal Variables – allow us to attach an
individual temporary property to VW and VPW
nodes; they can be accessed and shared by any
props associated with these nodes.
Different types of variables, especially when
used together, allow us to create efficient spatial
algorithms which work in between components
of distributed systems rather than in them.
Hierarchical Control:
DSL scenarios can use a variety of spatial control
rules, allowing us to assess local and remote
states, make local and global decisions, and
invoke or skip subsequent and terminate current
operations, on the results of these decisions.
Nested control infrastructures, embracing the
whole scenario, provide interdependent local and
global decisions associated with proper points of
the worlds.
2.3 The Language Syntax
DSL has a recursive syntax shown below together
with names of its main constructs (where square
brackets are for an optional construct, braces mean
construct repetition with a delimiter at the right, and
vertical bar separates alternatives).
wave Æ constant | variable | [ rule ] ({ wave , })
constant Æ number | string | special
variable Æ identifier | reserved
rule Æ expand | transfer | modify | branch |
advance | repeat | grant | echo |
arithmetic | structural | assign | compare |
timing | type | usage | identifier | wave
special Æ abort | thru | done | fail | any | random | all |
out | in | infinite | nil | empty | first | last |
andom | virtual | physical | combined |
neighbors | global | local | direct
reserved Æ N{alphameric} | H{alphameric} |
F{alphameric} | TYPE | QUALITIES |
NAME | ADDRESS | PLACE | WHERE |
BACK | PREVIOUS | LINK |
DIRECTION | ORDER | WHEN | TIME |
SPEED | STATE | VALUE | COLOR |
RESOURCES | DOER | USER | START
expand Æ hop | move | create | linkup
transfer Æ run | call | output
modify Æ split | partition | select | replicate | integer
branch Æ par | sequence | if | while | or | par or |
and | par and
advance Æ
advance | sync advance
repeat Æ cycle | loop | sling | repeat | repeat sync
grant Æ free | release | quit | none | lift | stay | grasp
echo Æ rake | min | max | sort | sum | average |
product | count | state
arithmeticÆ add | subtract | multiply | divide | degree
structuralÆ separate | unite | concatenate | append |
intersect | content | index | rand
assign Æ assign | assign peers
verify Æ equal | not equal | less | less equal | more |
more equal | empty | nonempty |
belong | not belong | inside | not inside
timing Æ sleep | remain
type Ænodal | heritable | frontal | environmental |
info | matter | number | string | wave
usage Æ address | name | place | center | range |
time | speed | doer | node | link | unit
PROVIDING SPATIAL INTEGRITY FOR DISTRIBUTED UNMANNED SYSTEMS
31
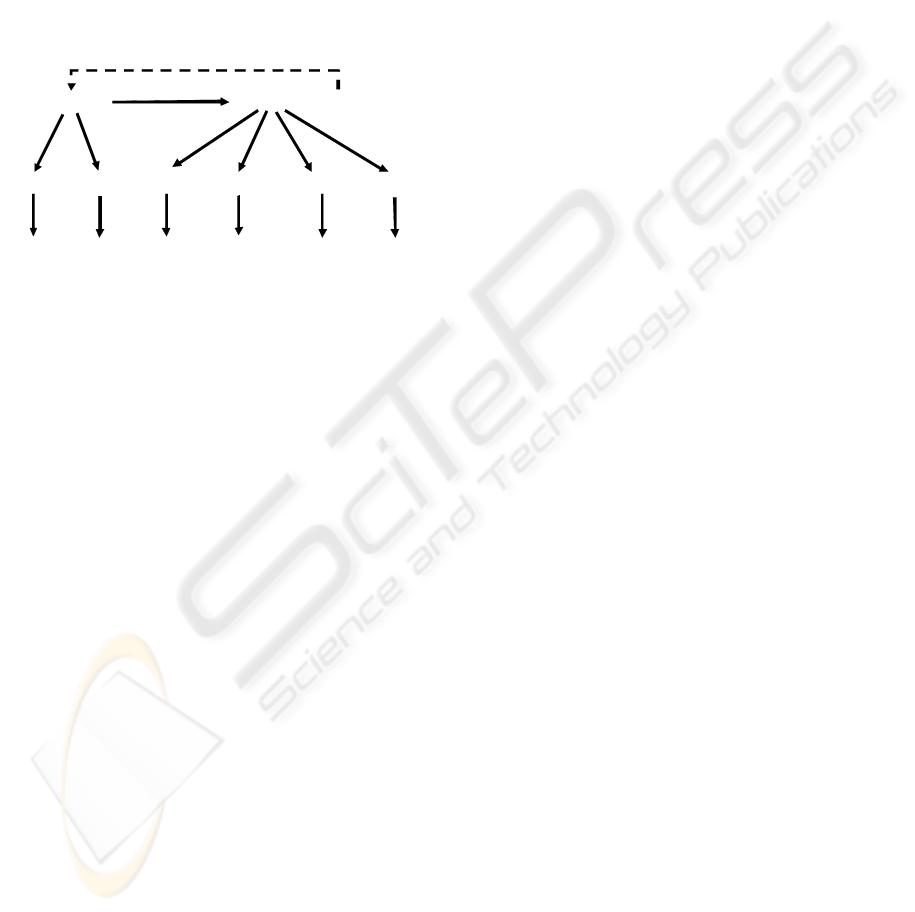
The DSL top level structure can also be expressed
graphically, as in Fig. 1. The basic construct, rule,
can represent any action or decision and can, for
example, be as follows:
Elementary arithmetic, string or logic operation.
Hop in a physical, virtual, or combined space.
Hierarchical fusion and return of (remote) data.
Distributed control, both sequential and parallel.
A variety of special contexts for navigation in
space, influencing operations and decisions.
Type or sense of a value, or its chosen usage,
guiding automatic interpretation.
constant
number
st rin g
sp ecial
identifier
reserved
wave
[ rule ] ( { wave , } )
variable
evolution
expansion
branching
advancing
repetition
granting
echoing
processing
combining
assignment
comparison
membership
linkage
type
usage
fusion verification essence
Figure 1: Recursive structure of DSL.
Different variants of this syntax and semantics
had been implemented for previous DSL subsets
(Sapaty, 1999, 2005), where conventional
expression of operations and delimiters between
program parts can be used too, say, for better
readability and compactness. For example:
add(3, 5, 7) same as 3 + 5 + 7
advance(w1, w2, w3) same as w1; w2; w3
where w1 to w3 may be arbitrary DSL programs
(waves) themselves. The first example could have
any programs instead of just numbers, each
returning its (possibly, remote and multiple) results,
as follows:
add(w1, w2, w3) same as w1 + w2 + w3
3 DISTRIBUTED INTERPRETER
A variety of options may be available for automatic
interpretation of DSL scenarios – from fully
centralized and sequential to fully distributed and
parallel. Due to peculiar syntax and semantics, the
language interpretation in distributed systems is
transparent and straightforward. Some basic features
of the DSL interpretation are as follows.
Direct association of props with world points
drastically simplifies bringing data from the
points to scenarios or vice versa: scenarios or
their parts to world points.
Chained actions can self-navigate and match the
world, while omitting used “heads” and
forwarding remaining “tails” further.
Independent actions can be launched in parallel,
developing autonomously in parts of the world.
The interpreter copy can be installed in internet
hosts, mobile robots, laptops, mobile phones,
smart sensors, or implanted into biological units.
The interpreter can also be a human being,
performing manually of what is for herself while
passing other parts of the scenario to other
human or electronic interpreters and establishing
dynamic command and control infrastructures
between them.
Any other systems can be accessed via the
networked interpreters, the latter forming a
supervisory layer managed in DSL.
The interpreter copies may be concealed inside
the systems to be impacted, even without their
knowledge (to work in hostile environments).
The interpreters can also migrate in the worlds to
be managed, collectively executing (mobile too)
mission scenarios, resulting altogether in a
flexible and ubiquitous system organization.
The DSL interpreter consists of a number of
specialized modules working in parallel and
handling and sharing specific data structures,
which are supporting both persistent virtual
worlds and temporary hierarchical control
mechanisms (Sapaty, 1999, 2005).
The heart of the distributed interpreter is its
spatial track system enabling hierarchical
command and control and remote data & code
access, also providing high integrity of emerging
parallel and distributed solutions, achievable
without central facilities.
In application to robotic communities, the
approach allows us to convert any group of mobile
robots into a goal-directed cooperative system by
integrating copies of the DSL interpreter, presented
as a universal control module U in Fig. 2, with
traditional robotic functionalities, as in
Kuhnert,
Krödel, 2005. (The figure exhibits mobile robots
which participated in M-ELROB 2008 trial).
Any mission scenario in DSL can start from any
robot, covering and tasking the whole system (or its
parts needed) at runtime and in parallel.
Subordination between the units and dynamic
command and control are established automatically,
as a derivative of the mission scenario and current
state of environment.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
32
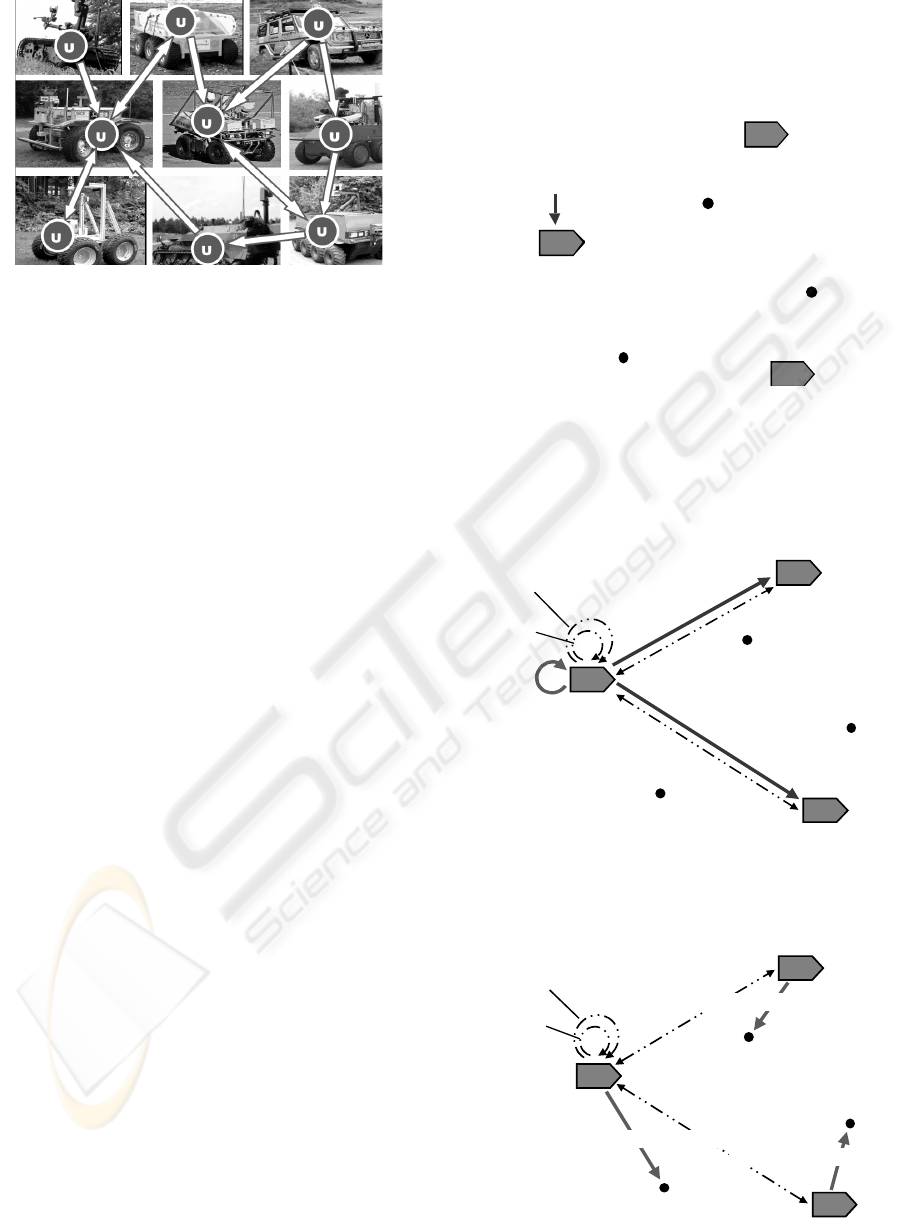
Figure 2: Heterogeneous robotic teaming using embedded
DSL interpreters.
Due to fully interpretive nature of the technology,
the scenarios can self-recover from any points,
timely reacting on failures of robots. The whole
group may remain fully functional and global-goal-
oriented even in case of indiscriminate damages to
individual units.
4 ELEMENTARY EXAMPLE
An elementary task to be programmed in DSL may
look like follows:
Go to given physical locations of the disaster
zone (represented in a proper system of coordinates
by the three locations): (50.433, 30.633),
(50.417, 30.490), and (50.467, 30.517). Evaluate
damage in each location, then find and transmit the
maximum destruction value on all locations,
together with exact coordinates of the corresponding
location, to a management center.
The corresponding program in DSL will be:
transmit(maximum(
move((50.433, 30.633),
(50.417, 30.490),
(50.467, 30.517));
attach(assess(damage),WHERE)))
This program reflects semantics of the task to be
performed in a distributed space, regardless of
possible equipment that can be used for this. The
latter may, for example, be a set of sensors scattered
in advance throughout the disaster zone, where
hopping by coordinates may result in a wireless
access of the sensors already present there, not
necessarily moving into these points physically.
As another solution, the program may task
mobile robots to move into these locations and
perform the needed damage assessment upon
reaching the destinations. We will be showing here
this latter option, using three available robots R1, R2,
and R3.
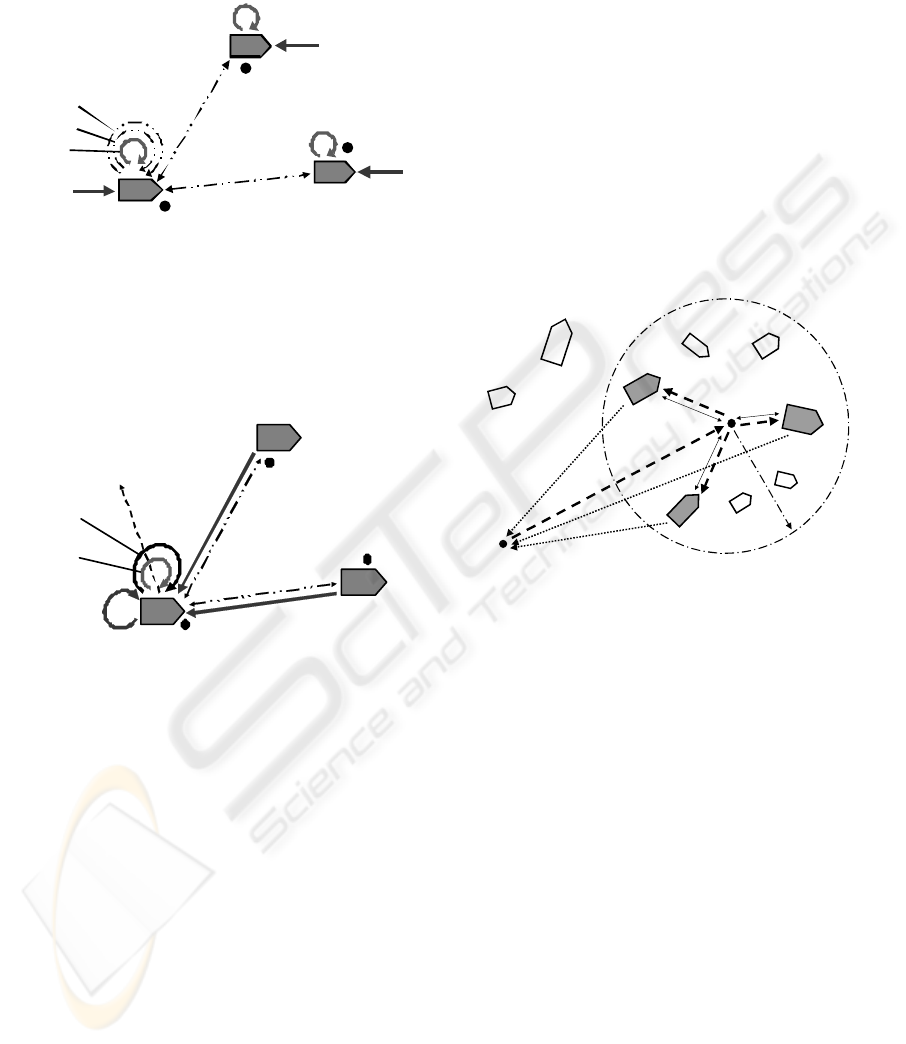
The possible starting position and initial scenario
injection (let it be into R1) are shown in Fig. 3.
50.417, 30.490
50.433, 30.633
50 .467 , 3 0.517
transmit(maximum(
move((50.433,30.633),
(50.417,30.490),
(50.467,30.517));
attach(assess(damage),WHERE)))
R1
R2
R3
Figure 3: Initial scenario injection.
After the creation of a distributed interpretation
infrastructure covering all three robots, R1 is
partitioning the scenario, and modifying and tasking
itself and the other two robots, as in Fig. 4.
move(50.467,30.517);
attach(assess(damage),
WHERE)
transmit
maximum
50.417, 30.490
50.433, 30.633
50.467, 30.517
DSL Interpretation
Infrastructure
move(50.467,30.517);
attach(assess(damage),
WHERE)
move(50.467,30.517);
attach(assess(damage),
WHERE)
R1
R2
R3
Figure 4: Parallel tasking of three robots.
All three robots then move independently to the
locations optimally chosen for them, as in Fig. 5.
DSL Interpretation
Infrastructure
50.417, 30.490
50.433, 30.633
50.467, 30.517
transmit
maximum
move(50.467,30.517)
move(50.417,30.490)
move(50.433,30.633)
R1
R1
R2
R3
Figure 5: Simultaneous robot movement.
PROVIDING SPATIAL INTEGRITY FOR DISTRIBUTED UNMANNED SYSTEMS
33
In each location reached independently by a
corresponding robot, the damage assessment and
exact coordinates return and attachment take place,
as in Fig. 6.
transmit
maximum
50.417, 30.490
5 0. 4 33 , 3 0. 6 33
50.467, 30.517
asse ss
assess
assess
O bser ved
damage
Obse rv ed
damage
Observed
da m a g e
R1
R2
R3
Figure 6: Simultaneous damage assessment.
And finally, R1, using rule maximum, finds global
maximum damage value from those obtained in each
of the three robots, and together with the
corresponding location coordinates transmits it to
the management center, as in Fig. 7.
transmit
maximum
Dam age leve l &
co or di n at e s
50 .4 17, 30 .4 90
50.433, 30.633
50 .4 67, 30 .5 17
Damage level &
coordinates
DSL interpretation
infrastructure
Dam age leve l &
coor dinate s
R1
R2
R3
Management
Ce nter
Figure 7: Merging data, finding global maximum.
As can be seen from the examples above, a semantic
level scenario describing what to do in the
distributed space, can be interpreted by robotic
teams autonomously, and by different numbers of
cooperating robots (we could use two or a single
robot instead). The number of available robots can
also vary at runtime, during the scenario evolution.
5 MORE ROBOTIC SCENARIOS
We will be using here the main scenarios that were
the basis of the M-ELROB 2008 trial.
5.1 Non-urban Reconnaissance
For this scenario, it is supposed that a group of
unknown vehicles is located in some distance in a
non-urban area (defined, say, with the position of a
center and area’s radius), with security situation
unclear there, so the reconnaissance should be done
by robotic vehicles for not risking own personnel.
The objective is to go to this target area and search
for vehicles with specific characteristics. If found,
they should be examined in detail, with their
parameters collected and reported to the control
station.
The general picture is shown in Fig. 8, where the
reconnaissance facilities should first go to the target
area (i.e. its center), observe the area by
cameras/sensors to roughly locate most probable
targets (by their size, for example). The next will be
to move directly to these selected targets and sense
& collect their detailed parameters, with sending the
results to the control point where they are stored and
analyzed.
Start
Target
area
Target
vehicles
Radius
Center
Find
Result 3
Move
Result 2
Result 1
Move
Figure 8: The reconnaissance scenario.
Parallel Solution. This, in DSL, may allow us to use
as many reconnaissance vehicles as possible (a
single one including), potentially involving
individual vehicles for each target identified, for
their detailed examination.
USER =(move(start); WHERE=center;
Targets=recognize(radius,features);
split(Targets); WHERE = VALUE;
collect(size, type, speed))
Explicitly Sequential Solution. The following DSL
program just details navigation and organization
procedures to execute the reconnaissance scenario in
a strictly sequential way, which may be useful for
optimization of the use of a single vehicle only.
move(start); WHERE = center;
Targets=recognize(radius,features);
loop(WHERE = withdraw(Targets,1);
Result &=collect(size,type,speed));
USER = Result
Avoiding Obstacles. The
movement to the target area and inside it may be
complicated due to presence of obstacles, as shown
in Fig. 9. The following DSL program, for the move
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
34
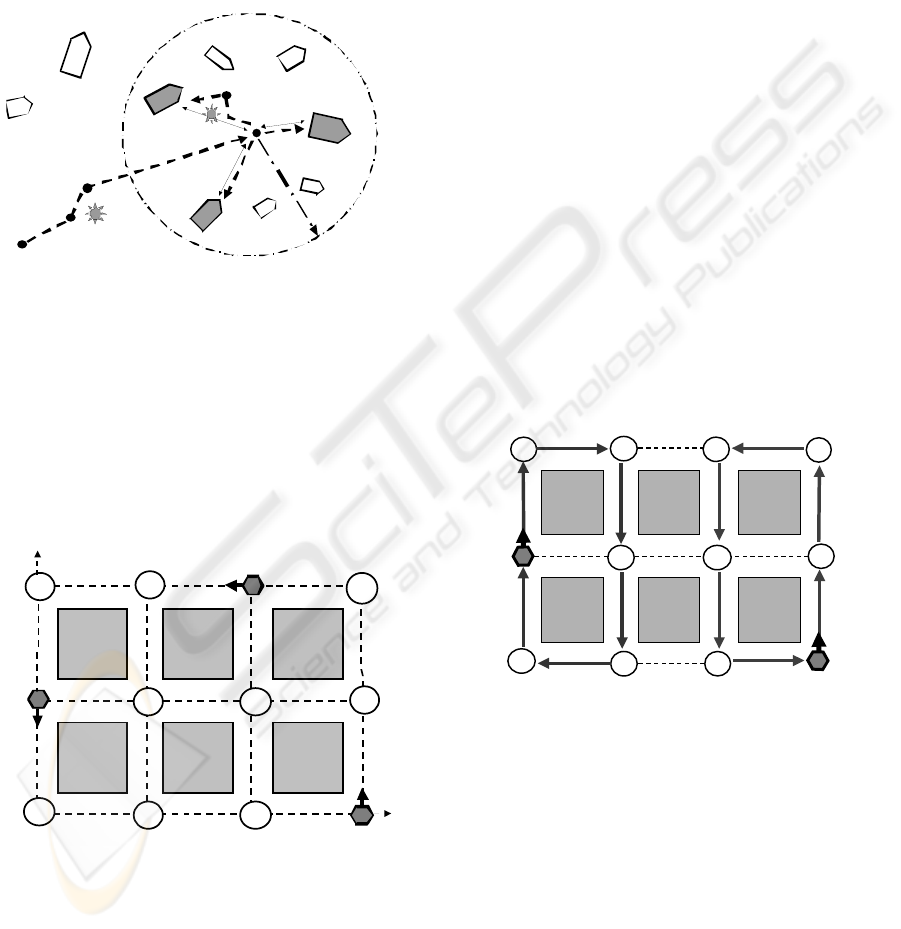
from Start to Center, uses an external procedure
approach_or_stop to detect obstacles and stop to
avoid collision, and the procedure
suitable to find
next suitable waypoint on the way to the destination,
from which the move should continue.
move(start);
loop(approach_or_stop(center);
WHERE != center;
WHERE = suitable(depth,center));
Start
Target
area
Target
vehicles
Radius
Center
Find
Move
Obstacle
Next
Next
Stop
Figure 9: Avoiding obstacles.
5.2 Camp Security
For the camp security scenarios, a defined urban
area has to be monitored (think military camp) and
this should be executed by robotic vehicles too, to
minimize risk to human personnel. The objective is
to detect and report irregularities in the area, like
intruders, while acquiring their positions and
imagery, and transmitting to control station.
1
3
2
5
46
Y
X
r
r
r
r
rr
r
r
r
r
r
r
rr
r
r
Robot 2
Robot 1
Rob o t 3
r
0_2
3_2
1_2
0_0
3_12_11_1
2_01_0
Figure 10: Camp security scenario.
The general picture is shown in Fig. 10, where
the camp units (numbered 1 to 6) are simultaneously
patrolled by a number of robotic vehicles moving
along the paths between and around the buildings.
Distributed Campus Map. The proper routing of
vehicles and resolution of possible conflicts between
them (like collision avoidance) can be assisted by
the creation of a distributed map of the campus area
(just reflecting Fig. 10) by the following DSL
program (with node names reflecting X-Y
coordinates of the crossings, and all links named r):
create(#3_1; F1=A; r#2_1; F2=A;
r#1_1; F3=A; r#0_1;(r#0_2; r#1_2;
r#F3, (r#2_2; r#F2,(r#3_2; r#F1))),
(r#0_0; r#1_0; r#F3, (r#2_0; r#F2,
(r#3_0; r#F1))))
Random Movement. The next program organizes the
duty performance by three parallel processes (which
may be executed by three robots) using the created
distributed map, with random choice of the next-hop
crossing and activation of the external service
procedure
move_check_report to analyze the
local security situation while on the move.
hop(0_1, 2_2, 3_0); WHERE = CONTENT;
repeat(or((hop(link(random));
grasp(Mark == nil; Mark = 1);
(hop(BACK); Mark) = nil;
move_check_report(CONTENT)), stay))
Movement via Predetermined Routes. If to use
predetermined routes only, like the ones shown in
Fig. 11 (one route using links named
r1 and another
one
r2), the collisions between robots can be
avoided in full.
1
32
546
r1
Robot 1
Robot 2
0_2
3_2
1_2
0_0
3_1
2_11_1
2_01_0
2_2
r1
r1
r1
r1
r1
r2
r2
r2
r2
r2
r2
r
r
r
r
r
Figure 11: Using predetermined routes.
Additional links r1 and r2 in the campus map can
be installed by the following DSL program:
Linkup((#0_2; r1#1_2; r1#1_1; r1#1_0;
r1#0_0; r1#0_1; r1#0_2),
(#3_2; r1#2_2; r1#2_1; r1#2_0;
r1#3_0; r1#3_1; r1#3_2))
And two independent spatial processes navigating
the campus via the new links (which may engage
two robots) can be organized by the following
parallel DSL code:
(hop(0_1); Flink = +r1),
(hop(3_0); Flink = +r2);
PROVIDING SPATIAL INTEGRITY FOR DISTRIBUTED UNMANNED SYSTEMS
35
WHERE = CONTENT;
repeat(hop(link(Flink));
move_check_report(CONTENT))
Any imaginable combinations of different types of
simultaneous movement through the camp (like
those by predetermined routes and/or by free,
random, wandering) with collision avoidance can
also be easily organized in DSL.
5.3 Transport Convoy
Imagine there is a delivery for a camp located in
some distance. The objective is to move at least two
vehicles to the target location, where only the first
one can be manned and the second should follow the
route of the first one, on a certain distance from it.
We will consider a fully robotic solution for such a
convoy, with two and also any number of vehicles,
where only the first vehicle knows (and follows)
waypoints toward the target location, while others
dynamically chaining with, and following the
previous ones on the move.
Two-unit Convoy. It is represented by the
communicating Leader and Follower, where the
first one defines its movement by a sequence of
waypoints, and the second one, regularly requesting
the Leader, moves to the positions previously
occupied by it, while keeping a certain threshold
distance. This is shown in Fig. 12, and by the DSL
program that follows.
Waypoints
Range
Leader
Follower
Start
Leader,
Follower
Figure 12: Two-unit convoy.
move(start);
(create(Leader);
Waypoints = (w1, w2, w3, …);
loop(WHERE = withdraw(Waypoints,1))),
(create(Follower); sling(
Lcoord = (hop(range, any); WHERE);
distance(WHERE, Lcoord) > threshold;
WHERE = Lcoord))
Multiple-unit Convoy. A scenario for the convoy
with any number of chained processes (to be
materialized by robotic units) is described by the
following DSL program and depicted in Fig. 13. For
this case, only the first process is a pure leader and
the last process a pure follower, while all other
processes combine both functionalities, i.e. being
followers for the previous processes and leaders for
the subsequent ones.
move(start);
cycle(N < number; create(N += 1));
(NAME == 1; Waypoints = (w1,w2,w3,…);
Loop(WHERE = withdraw(Waypoints,1))),
(NAME != 1; sling(
Lcoord = (hop(range,NAME-1); WHERE);
distance(WHERE, Lcoord) > threshold;
WHERE = Lcoord))
Waypoints
Range
Leader
Leader
Follower
Leader
Follower
Leader
Follo wer
Follower
Start
1
5
3
4
2
Nodes:
1, 2, 3, 4, 5
Figure 13: Multiple-unit convoy.
5.4 Transport Mule
Fir this scenario, there are two camps with a certain
distance in between, and a cargo with a given weight
should be transferred between the camps. We will
consider here different possibilities to deliver
payload between the camps, using unmanned
vehicles as “mules”.
In a Single Piece. This may be the case if cargo’s
weight allows it to be put on a single vehicle, as
shown ion Fig. 14.
Car go
Campus2Campus1
Figure 14: Single piece cargo delivery.
Limit
Campus2Ca m pu s1
Figure 15: Shuttling delivery.
The related DSL program will be as follows:
move(Campus1);
frontal(Cargo) = “substance”;
move(Campus2); Store = Cargo
Shuttling between Camps. For this option, the
process shuttles as often as possible between the two
camps after partitioning the cargo into portions for
the weight allowed, unless all the cargo is delivered,
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
36

as shown in Fig. 15 and by the following program.
move(Campus1); frontal(Load);
Cargo = “substance”; Limit = 50;
loop(or((weight(Cargo) > Limit;
Load = withdraw(Cargo,Limit)),
(weight(Cargo) > 0; Load = Cargo));
hop(Campus2); Store += Load;
hop(Campus1))
Multiple, Parallel Delivery. For this case, different
processes (vehicles) are considered to be
independent from each other, each moving to the
destination as quickly as possible on its own (see Fig.
16 and the following program).
move(Campus1); frontal(Load);
Cargo = “substance”; Limit = 50;
cycle(or((weight(Cargo) > Limit;
Load = withdraw(Cargo, Limit)),
(weight(Cargo) > 0; Load = Cargo)));
move(Campus2); Store += Load
Limit
Limit
Limit
Limit
…
Campus2
Campus1
Figure 16: Parallel cargo delivery.
Multiple, Convoy Delivery. For this scenario, the
vehicles, each with a limited partition of cargo, are
dynamically chaining in a column for a cohesive
movement towards the destination (see Fig. 17 and
the subsequent DSL program).
move(Campus1); frontal(Load);
Cargo = “substance”; Limit = 50;
cycle(or((weight(Cargo) > Limit;
Load = withdraw(Cargo, Limit)),
(weight(Cargo) > 0; Load = Cargo));
create(N += 1));
(NAME == 1; move(Campus2)),
(NAME != 1; loop(WHERE != Campus2;
WHERE = (hop(NAME-1); WHERE));
Store += Load
Limit
Limit
Limit
…
Limit
Campus2
Campus1
Figure 17: Delivery in a convoy.
5.5 Explosive Ordnance Disposal
Explosive Ordnance Disposal (EOD) means the
detection, identification, onsite evaluation, rendering
safe, recovery, and final disposal of Unexploded
Ordnance (UXO) including detonation and burning.
It is often said that the EOD operation is a 3 Ds one,
which is Dangerous, Dirty and Demanding (or
Difficult) job. Using robotic vehicles, especially
multiple ones, is therefore becoming the most
promising EOD option.
Various kinds of EOD scenarios for navigation
and examination of the target territory may be
offered. We will just hint here on the simplest two
options, easily expressible in DSL.
Sequential Territory Search. This represents a
single-thread process (oriented on a single vehicle),
where the whole territory is incrementally scanned
unless all being searched, as described by the
following program and depicted in Fig. 18.
X1
X2
Y1
Y2
DY
Start
Finish
Figure 18: Sequential navigation.
X1 =…; X2=…; Y = Y1 =…; Y2 =…; DY =…;
loop(WHERE = (X1,Y); WHERE = (X2,Y);
(Y += DY) < Y2; WHERE = (X2,Y);
WHERE = (X1,Y); (Y += DY) < Y2)
The sequential coverage of the territory can be
organized with minimum waypoints to pass, in a
zigzag way, as shown in Fig. 19 and by the
following program.
X1
X2
Y1
Y2
DY
Start
Finish
Figure 19: Sequential zigzag navigation.
X1 =…; X2=…; Y = Y1 =…; Y2 =…; DY =…;
loop(WHERE = (X1,Y); (Y += DY) < Y2;
WHERE = (X2,Y); (Y += DY) < Y2)
Another solution, starting from the region’s
periphery and then gradually moving to its center, is
shown in Fig. 20, and by the next DSL program.
PROVIDING SPATIAL INTEGRITY FOR DISTRIBUTED UNMANNED SYSTEMS
37
X1
X2
Y1
Y2
Start
DY
DX
Fin ish
Figure 20: Sequential out-in navigation.
X1 = …, X2 = …; Y1 = …; Y2 = …;
DX = …; DY = …; X = X1; Y = Y1;
DDX = X2 – X1; DDY = Y2 – Y1; N = 1;
WHERE = (X,Y);
loop(Y += DDY * N; WHERE = (X,Y);
X += DDX * N; WHERE = (X,Y);
(DDX -= DX) > 0; (DDY -= DY) > 0;
N *= -1)
Parallel Territory Search. This
can be represented by a number of independent
processes, each starting from a different location,
and navigating altogether the whole region in
parallel, as depicted in Fig. 21, and explained by the
DSL program that follows (taking into account that
all processes follow predetermined routes for this
case).
X1 X2
Y1
Y2
DY
S
t
a
r
t
F
i
n
i
s
h
Figure 21: Parallel predetermined navigation.
X1 =…; X2=…; Y1 =…; Y2 =…; DY =…;
frontal(Y) = Y1; DDY = 0;
cycle((Y += DDY) < Y2; DDY += DY);
WHERE = (X1,Y); WHERE = (X2,Y)
Parallel search of the territory can also be organized
in a random way, where each process randomly
chooses its next hop, also taking into account that
the chosen next destination should not have been
visited before (at least to look like this, with the help
of visual sensors). Parallel random search may have
an advantage before predetermined search in that it
can eventually cover all the territory despite possible
failures of individual processes (robots). Such a
search, with processes starting from some initial
points (named
c1 to c5), where processes also keep
certain threshold distance from each other, is shown
in Fig. 22 and by the following program.
X2
Y1
Y2
X1
Range
Random
New
Random
Random
c1
c2
c3
c4
c5
Figure 22: Parallel random navigation.
move(c1, c2, c3, c4, c5); Range = …;
X1 =…; X2=…; Y1 =…; Y2 =…; D =…;
loop(New = WHERE + 2(random(-D, D));
inside(New, (X1, X2, Y1, Y2));
hop(New, Range) & seen(New) == nil;
shift_check_act(New))
6 OTHER APPLICATIONS
Many other applications of the paradigm are
possible, as follows, some of which already
investigated, tested, and published (Sapaty, 1999,
2002, 2005, 2007, 2008, 2008a;
Sapaty, Sugisaka,
Finkelstein, Delgado-Frias, Mirenkov, 2006; Sapaty,
Morozov, Sugisaka, 2007
).
Emergency Management. Using interpreters
installed in massively wearable devices may allow
us to assemble workable systems from any wreckage
after the disasters, using any remaining
communication channels, manual including. These
emergent systems can provide distributed self-
awareness, collect statistics of casualties, guide the
delivery of relief goods, and coordinate collective
escape from the disaster zone.
Directed Energy Systems.
The technology can
provide high flexibility in organizing directed
energy (DE) systems, especially in crisis situations,
making automatic distributed decisions with the
“speed of light” too. It may also help automate the
global power dominance by optimized delivery of
directed energy into any world points via
dynamically organized networks of relay mirrors.
Distributed Avionics.
Implanting interpreter copies
into main control points of the aircraft may provide a
higher, intelligent, layer of its self-analysis and
recovery, by the spreading recursive scenarios
starting from any point and collecting & fusing key
data from other points. The embedded interpretation
network with local, dynamic, and emergent links
will be fully functional under any damages,
especially with wireless communications between
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
38

the interpreters. This may always provide global
control integrity, even in a physically disintegrating
object, helping to save lives and complete missions.
Sensor Networks. Wireless sensors may be dropped
from the air massively, as “smart dust”. Having a
limited communication range, they must operate in a
network to do nonlocal jobs in a distributed
environment. With the technology offered, we can
convert their emergent networks into a universal
parallel computer operating in DSL. It can
effectively solve complex distributed problems--
from just collecting and fusing scattered data to
outlining and assembling images of the distributed
phenomena like, for example, flooding, smog, flocks
of birds, movement of troops, etc.
Advanced Command and Control. In DSL, it is
possible to define high-level scenarios concentrating
on mission goals and top decision-making while
delegating C2 routines, appearing at runtime as a
derivative of the mission and environment states, to
automatic interpretation. It is also convenient to
express in DSL any theoretical and practical issues
of advanced C2 explicitly.
Infrastructure Protection. Navigating the systems at
runtime, the technology can analyze safety and
integrity of critical infrastructures and key resources,
establishing protective networked mechanisms
throughout them. Other systems can be involved
from the WPT layer for emergent infrastructure
protection and recovery, including air and space
defense, police and army. In relation to energy
infrastructures, the technology can help observe
power networks from the air or ground, trace
electric, gas, or oil supply lines, sensing their states
(and, if needed, directly accessing the disaster
zones), also providing regular or emergent sentry
duties at power installations, etc.
Global and Battlespace Dominance. The DSL
scenarios, using any electronic media, can self-
spread, outline, and grasp distributed systems of
different natures while establishing global
dominance over them. They can analyze their
internal infrastructures, finding strong and weak
points, orient behavior, or destroy the infrastructures
or the system as a whole if required. The approach,
as an intelligent self-recovering super-virus, which is
difficult to discover and kill by traditional means,
can effectively employ advanced robotic facilities,
like swarms of aerial and ground vehicles, to attack
adversarial systems.
7 GESTALT-RELATED
Our approach may be considered as one of the first
attempts to formalize and implement the notion of
gestalt (Wertheimer, 1924), under which the whole
dominates over parts (being greater than the sum of
them), with parts having sense only in the context of
the whole, rather than vice versa. Gestalt theory
represented the main departure from atomistic vision
of systems at the beginning of the last century. Many
existing systems, especially distributed ones, are still
based on the concept of predetermined parts (agents)
that communicate with each other in an attempt to
get the global behavior needed. The latter, with
rapidly growing number of agents in complex
systems and starting from the agents level is
becoming more and more problematic.
Within the approach offered, we have come to
quite a different and higher level model of the
system organization. Abstracting from system parts
and their interactions, which may be emergent and
varying at runtime, we can describe the needed
global system behavior on a semantic level, where
parts and their interactions may not be known in
advance, and may dynamically appear (disappear
too) just to maintain the global behavior needed.
The technology developed allows us to
automatically interpret global system scenarios in
any networked systems (comprising internet hosts,
laptops, mobile robots, mobile phones, smart sensors,
and/or humans themselves). It allows us to get even
higher—to describe what the system should do on
the highest level, where its local and global behavior
is a derivative of this description, which, in its turn,
makes the system structures and operation as a
further derivative.
8 CONCLUSIONS
A novel ideology and technology, converting any
distributed system into a universal spatial machine
capable of solving complex problems on itself and
on the surrounding environments, has been
presented. This conversion can be achieved by
implanting into the system sensitive points and its
active doers, humans and robots including, of the
same copy of a universal control module,
communicating with other such modules via
available channels. Their entire network, which may
be dynamic and emergent, collectively interprets
mission scenarios written in a special high-level
language, which are defining system’s internal and
external behavior.
PROVIDING SPATIAL INTEGRITY FOR DISTRIBUTED UNMANNED SYSTEMS
39

Created and modified on the fly, the scenarios
can start from any component, covering the system
at runtime through the cooperating interpreters.
During the scenario evolution, any operations can be
carried out throughout the distributed world, along
with the needed movement of code, equipment and
artificial or biological doers, humans including, as
well as creation and maintenance of physical and
virtual infrastructures supporting the missions.
The approach offered can dramatically simplify
application programming in distributed systems,
especially robotized ones. As can be seen from the
examples throughout this paper, programming multi-
robot scenarios in distributed and dynamic
environments in DSL may not be more difficult than,
say, programming of routine data processing tasks in
traditional languages like Fortran, C, or Java.
The distributed robotized systems are of rapidly
growing importance in many areas, and especially in
defense, where robotic swarming on asymmetric
battlefields is becoming a major dimension of the
new military doctrine for the 21
st
century (Singer,
2009). The written above is much in line with these
trends, allowing us to flexibly combine loose
swarming with more classical command and control,
which can help gradually transform fully manned
into mixed and ultimately totally unmanned systems.
Other prospective applications of this work can
be linked with economy, ecology and weather
prediction—by using the whole networked world as
a spatial supercomputer, self-optimizing its
performance.
The approach offered may also be compared
with the invention of the first world computers and
first high-level programming languages (Zuse,
1948/49; Rojas, 1997). In our case, this computer
may not only operate with data stored in a localized
memory, but can cover, grasp, and manage any
distributed systems, the whole world including, and
can work not only with information but with
physical matter or physical objects too.
ACKNOWLEDGEMENTS
This work has been funded by the Alexander von
Humboldt (AvH) Foundation in Germany. Special
thanks to Klaus-Dieter Kuhnert and Matthias Langer
for sheltering this activity at the University of
Siegen. Years of cooperation with Robert
Finkelstein (Robotic Technology Inc., USA) and
Masanori Sugisaka (Nippon Bunri University,
Japan) contributed much to the ideas expressed in
this paper. The support of this ideology and
technology by Joaquim Filipe (Escola Superior de
Tecnologia, Portugal) and by ICINCO conferences
was really invaluable. Encouragement from Stephen
Lambacher (Aoyama Gakuin University, Japan) has
been appreciated too.
REFERENCES
Kuhnert, K.-D., Krödel, M., 2005. Autonomous Vehicle
Steering Based on Evaluative Feedback by
Reinforcement Learning. MLDM.
M-ELROB, 2008. Military European Land-Robot Trial.
Hammelburg, Germany.
Rojas, R., 1997. Konrad Zuse’s Legacy: The Architecture
of the Z1 and Z3. IEEE Annals of the History of
Computing. Vol. 19, No. 2.
Sapaty, P. S., 1999. Mobile Processing in Distributed and
Open Environments, John Wiley & Sons. New York.
Sapaty, P. S., 2002. Over-Operability in Distributed
Simulation and Control. The MSIAC's M&S Journal
Online. Winter Issue, Volume 4, No. 2, VA, USA.
Sapaty, P. S., 2005. Ruling Distributed Dynamic Worlds,
John Wiley & Sons. New York.
Sapaty, P., Sugisaka, M., Finkelstein, R., Delgado-Frias, J.,
Mirenkov, N., 2006. Advanced IT Support of Crisis
Relief Missions. Journal of Emergency Management,
Vol. 4, No. 4.
Sapaty, P., Morozov, A., Sugisaka, M., 2007. DEW in a
Network Enabled Environment. Proc. International
conference Directed Energy Weapons 2007. Le
Meridien Piccadilly, London, UK.
Sapaty, P., 2007. Intelligent management of distributed
sensor networks, In Sensors, and Command, Control,
Communications, and Intelligence (C3I) Technologies
for Homeland Security and Homeland Defense VI, ed.
by E. M. Carapezza. Proc. of SPIE Vol. 6538, 653812.
Sapaty, P., 2008. Distributed Technology for Global
Dominance. Proc. of SPIE, Volume 6981, Defense
Transformation and Net-Centric Systems 2008. Raja
Suresh, Ed., 69810T.
Sapaty, P., 2008a. Grasping the Whole by Spatial
Intelligence: A Higher Level for Distributed Avionics.
Proc. International Conference Military Avionics
2008. Cafe Royal, London, UK.
Sapaty, P., 2009. Gestalt-Based Ideology and Technology
for Spatial Control of Distributed Dynamic Systems.
Proc. International Gestalt Theory Congress, 16th
Scientific Convention of the GTA. University of
Osnabrück, Germany.
Singer, P. W., 2009. Wired for War: The Robotics
Revolution and Conflict in the 21
st
Century, Penguin.
Wertheimer, M., 1924. Gestalt Theory, Erlangen. Berlin,
1925.
Zuse, K., 1948/49. “Uber den Plankalk, als Mittel zur
Formulierung schematisch kombinativer Aufgaben”,
In Archiv Mathematik, Band I.
ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics
40
