DCADH: A GENERATING ALGORITHM OF

DELAY-CONSTRAINED MULTICAST ROUTING TREE

Yu-xi Zhu and Ling Zhou

Department of Computer Science and Technology, Foshan University, Foshan, Guangdong, China

Keywords: Multicast Routing, Average Distance Heuristic, Delay-Constrained, Least-Cost, Simulation.

Abstract: Multicast is the ability of a communication network to accept a single message from an application and

to deliver copies of the message to multiple recipients at different location. With the development of

Internet, Multicast is widely applied in all kinds of multimedia real-time application: distributed

multimedia systems, collaborative computing, video-conferencing, distance education, etc. In order to

construct a delay-constrained multicast routing tree, average distance heuristic (ADH) algorithm is

analyzed firstly, then by using which a delay-constrained algorithm called DCADH is presented．By

using ADH a least-cost multicast tree can be constructed; if the path delay can’t meet the delay upper

bound，a shortest delay path which is computed by Dijkstra’s algorithm will be merged into the existing

multicast tree to meet the delay upper bound. Simulation experiments show that DCADH has a good

performance in achieving a low-cost multicast tree.

1 INTRODUCTION

QoS-aware group communication has accelerated

the need and application of multicast, for example,

video-conference, distance education, resource

location, distributed simulation, etc. Multicast

routing algorithm is a key issue in group

communication, only by which a multicast routing

tree can be constructed correctly and efficiently. In

most conditions, it is NP-Complete and defined as a

Steiner tree problem.

From the view of managing and optimizing

network resource, it requires that the multicast tree

constructed by the multicast routing algorithm with

a least cost in order to optimize the network

resources. Taking service of quality (QoS) of the

multicast communication into consideration, the

multicast trees should meet the stringent

requirements of QoS constraints. when both the cost

and the delay need be considered to optimize, the

problem of delay-constrained least-cost (DCLC)

multicast routing is put forward. The DCLC

problem is the most common and important issues

among the QoS-constrained multicast routing

problems.

Different algorithms have been proposed to

address the multicast routing problem (Salama H. F.,

1997). Some optimized the tree cost, such as KPP,

BSMA. Some simplified the time complexity, such

as SPT, CDKS. And some others focused on how to

meet the quality of service. But it is very hard to use

any one to optimize all those parameters at the same

time.

In this paper, we concentrated on how to solve

the DCLC problem by using average distance

heuristic (ADH) algorithm.

2 RELATED WORK

Salama and other scholars have had a

comprehensive comparative study of the algorithm

which solved the DCLC problem and drew a

conclusion that there were some currently mature

DCLC algorithms such as KPP, CDKS, BSMA, and

so on. But because of the higher cost of spanning

tree or higher computational complexity, they were

some difficulty to apply to the actual network

communication.

In addition, some scholars solved the DCLC

problem using the heuristic algorithms based on

new optimization theories, including neural

networks, genetic algorithms, simulated annealing,

tabu algorithm, etc (G. Feng, C. Douligers, 2001).

Some of those bring about uncertainty in theory

analysis and convergence, some are with higher

181

Zhu Y. and Zhou L. (2009).

DCADH: A GENERATING ALGORITHM OF DELAY-CONSTRAINED MULTICAST ROUTING TREE.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 181-184

DOI: 10.5220/0002182501810184

 SciTePress

complexity of time, Moreover, with some specific

parameters introduced by those algorithms.

As part of our ongoing research in multicast

routing algorithm, we have developed

delay-constrained multicast routing algorithm with

mininum path heuristic (MPH) which is an

excellent algorithm to construct a DCLC multicast

tree. By using the algorithm a computing

destination node can join the multicast tree by

selecting the path which has the least cost value to

the existing multicast tree; if the path delay does not

meet the delay upper bound, a shortest path tree

based the delay will be merged into the existing

multicast to meet the delay upper bound.

Recently, we have researched the multicast

routing problem in mobile IP. In order to reduce the

transmission delay and minimize the joined latency,

we introduced an idea of bone node set. Based on

the idea a multicast routing algorithm called bone

node set-based multicast routing algorithm

(BNSBMR) was designed. It characters itself in

three aspects. Firstly, it can optimize the cost of

multicast delivery tree and reduce the bandwidth

consumption by using bone node set. Secondly, it

can reduce the latency of handover, which is helpful

for mobile node to achieve a fast handover. Thirdly,

the transmission delay for multicast packet is

lessened by sharing those bone nodes.

Moreover, we have also researched the

problem of a delay-constrained dynamic multicast

routing. Based the greedy idea a dynamic multicast

routing algorithm called delay-constrained dynamic

greedy algorithm (DCDG) was presented to

construct a dynamic multicast tree. In the resulting

tree the delay from the source to each destination

node is not destroy the delay upper bound.

At the same time, we discussed their

correctness in theory and experimented their delay

and cost performance by random network model.

3 DCADH ALGORITHM

A communication network can be modeled by an

edge weighted G=(V, E) where V is a set of host or

router nodes and E is the set of communication

links. We assume that the cost weight (u, v) is

nonnegative value for each link (u,v) E. Given a

source s and a set of destinations D,

Definition 1 (shortest path): We call the path

from u to v a shortest path if the total path weight

from v to u is the minimize one and we write the

shortest path path(u, v).

Definition 2 (multicast routing tree): A

multicast routing tree is a rooted subtree of the

graph G whose root is s, which includes all the

routing paths from s to D.

Definition 3 (delay-constrained least-cost

multicast routing tree): Given network G (V, E),

multicast source s, destination node set D, and the

delay upper △

Delay

, if a multicast tree T covers s

∪

and is satisfied with the following conditions:

}

,),(

)()(min{)(

∑

∈

∑

∈

DvvsPe

eCostTCostTCost

∑

∈

Δ≤

),(

)()),((

)),((..

vsPe

Delay

eDelayvsPDealy

vsPDelayts

(

∈

∀

TvsP ∈),(

we call the tree T as a DCLC multicast routing tree,

that is, delay-constrained steiner tree.

The problems of constructing a DCLC

multicast routing tree is NP-complete, which is

usually solved by designing a heuristic algorithm. In

this paper, we concentrated on how to solve the

DCLC problem by using average distance heuristic

(ADH) algorithm.

3.1 The Basic Idea

The basic idea of DCADH algorithm has been

two-fold. Firstly, the ADH algorithm (Yu Y. P., Qiu

P. L., 2002)

is used to calculate a low-cost multicast

routing tree T. Secondly, if T does not meet the

delay constraint △

delay

, Dijkstra shortest path tree

algorithm is used to compute the least-delay tree T,

and the shortest path based the delay will be merged

into the existing multicast to meet the delay upper

bound. So a low-cost multicast routing tree which

meets the delay upper will be constructed. When the

least-delay path was merge into the low-cost

multicast tree a new loop may appear, so we

designed a process to eliminating the loops.

The detail descriptions of the algorithm

process are as follows:

Step 1: Firstly set s as the least-delay tree;

then compute a least-delay tree spanning all the

destination members by Dijkstra shortest path tree

(SPT) algorithm. If the delay of T Delay (

) >△

delay

then exit;

Step 2: according to ADH algorithm, set all the

multicast member nodes as the initial set of T ;

Step 3: Calculate f (v) = min ( d (v, Vj) + d (v,

Vj) ), which Vi, Vj is the node set of arbitrary two

separation trees. As for v ∈ V, if f (v) is minimum ,

Ti will link Tj through v, and the paths are P (v, Vi)

and P (v,Vj);

Step 4: Modify set T and node sets, k = k-1;

Step 5: Repeat steps 3 and 4 until k = 1;

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications

182

Step 6: Determine the delay constraint in the

multicast tree. As for

∈

∀

, if

⋅

)(delay

Path(m, s)∈T

Delay

will been merged into T;

Step 7: If a loop is formed, the process of

elimination loop will be introduced by changing the

node’s father;

Step 8: Repeat Step 6 until all the nodes meet

the delay constraints.

3.2 Performance Analysis

Theorem 1. Only when ADH tree does not meet

delay-constraint and the least-delay path is merged

into the multicast, DCADH spanning tree might

appear loops; otherwise there are no loops in

DCADH spanning tree.

Theorem 2. Only when there are at least two tree

nodes on the path at the same time, the loops might

appear; otherwise there are no loops in DCADH

spanning tree.

Theorem 3. There are no loops in the multicast tree

⇔ All the tree nodes besides the root node in the

spanning tree have only one father node.

Theorem 4. As long as there exists a multicast tree

T which meets the delay constraints, DCADH can

find the low-cost delay-constraint multicast routing

tree .

Proof: see reference (Zhou L., Sun Y. M., 2008).

Theorem 5. The time complexity of DCADH

algorithm is O (n

3.3 Simulation Experiments

Waxman firstly put forward a network model to

generate random topology in 1988 (Waxman B. M.,

1988). Waxman’s algorithm set the number of

network nodes, then decide whether there is a direct

link connected between nodes u and v according to

the following probability P

(,)

(,) exp

luv

Puv

−

The specific simulation parameters see Table 1.

Table1: Simulation parameters.

Parameters Description Value

N network scale 20-120

number of destination

nodes

20-80

α between 0-1 0.3

β between 0-1 0.3

Cost(·) cost of links between 1-5

V transmission speed 2×10

m/s

elay

upper delay 0.01-0.1s

Each experimental data test 10 random

networks, each network measures 100 times, for a

total of 1000 times, then we take the average value

as the experiment measure value. At the same time,

its performance is compared with CDKS

(Sahasrabuddhe L. H., Mukherjee B., 2000), KPP

(Kompella V. P., Pasquale J. C., and Polyzos G. C.,

2000) in the cost and delay.

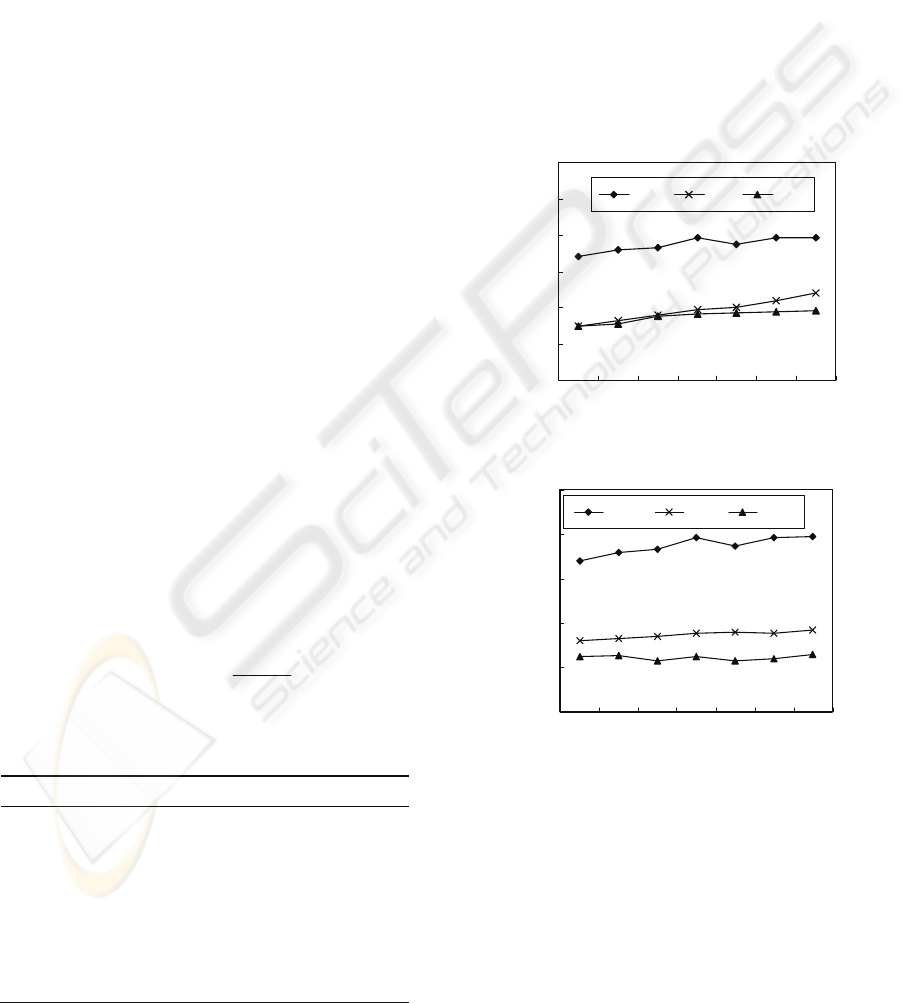
Experiment 1. Measuring the relation between the

cost of multicast routing tree and the network node

number. 20 fixed member nodes unchanged, the

number of network node size begins from 60 and

every time increases 10. The experiment results

shown in Figure 1(a) for △

delay

= 0.03s and (b) for

△

delay

= 0.06s.

100

150

200

250

300

60 70 80 90 100 110 120

Number of nodes

Cost

CDKS KPP DCADH

(a) △

delay

= 0.03s.

100

150

200

250

60 70 80 90 100 110 120

Number of nodes

Cost

CDKS KPP DCADH

(b) △

delay

= 0.06s.

Figure 1: The relation of tree cost and network scale.

Experiment 2. Measuring the relation between the

tree cost and the size of the group. 100 nodes of

fixed network scale unchanged, the number of

member nodes change from 20 to 80 and every time

increases 10. The results shown in Figure 2 (a) for

△

delay

= 0.03s and (b) for △

delay

= 0.06s.

DCADH: A GENERATING ALGORITHM OF DELAY-CONSTRAINED MULTICAST ROUTING TREE

183

100

200

300

400

500

600

700

20 30 40 50 60 70 80

Number of members

Cost

CDKS KPP DCADH

(a) △

delay

= 0.03s.

100

200

300

400

500

600

700

20 30 40 50 60 70 80

Number of members

Cost

CDKS KPP DCADH

(b) △

delay

= 0.06s.

Figure 2: The relation of tree cost and the group size.

4 CONCLUSIONS

Through the theoretical analysis and simulation to

DCADH algorithm, we can see that DCADH

algorithm can not only correctly construct a

low-cost multicast routing tree, but also meet the

delay upper. Compared with some similar DCLC

algorithms, it achieves a good performance in cost

and delay. DCADH is an excellent DCLC heuristic

algorithm.

ACKNOWLEDGEMENTS

The authors would like to thank the anonymous

reviewers for their good suggestions, comments, and

feedback to improve the presentation of this paper.

REFERENCES

Salama H. F., 1997. Evaluation of Multicast Routing

Algorithm for Real-Time Communication on

High-Speed Networks[J]．IEEE Journal on Selected

Areas in Communication.

Feng G., Douligers C., 2001. A Neural Network Method

for Minimum Delay Routing in Packet Switched

Networks[J]. Computer Communication.

Yu Y. P., Qiu P. L., 2002. An improved algorithm for

Steiner trees. Journal of China Institute of

Communications.

Zhou L., Sun Y. M., 2008. A Delay-Constrained Steiner

Tree Algorithm Using MPH. Journal of Computer

Research and Development.

Waxman B. M., 1988. Routing of Multipoint

Connections[J]. IEEE Journal on Selected Areas in

Communications.

Sahasrabuddhe L. H., Mukherjee B., 2000. Multicast

Routing Algorithms and Protocols: A Tutorial. IEEE

Network.

Kompella V. P., Pasquale J. C., and Polyzos G. C., 2000.

Multicasting for multimedia applications [C]. Proc.

IEEE INFOCOM’9.

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications

184