
PARAMETER OPTIMIZATION IN TIME-FREQUENCY ε-FILTER
BASED ON CORRELATION COEFFICIENT
Tomomi Abe
Waseda university, 55N-4F-10A, 3-4-1 Okubo, Shinjuku-ku, Tokyo, 169-8555, Japan
Mitsuharu Matsumoto
The University of Electro-Communications, 1-5-1, Chofugaoka, Chofu-shi, Tokyo, 182-8585, Japan
Shuji Hashimoto
Waseda university, 55N-4F-10A, 3-4-1 Okubo, Shinjuku-ku, Tokyo, 169-8555, Japan
Keywords:
Noise reduction, Parameter optimization, ε-filter, Time-frequency domain.
Abstract:
Time-Frequency ε-filter (TF ε-filter) can reduce most kinds of noise from a single-channel noisy signal with
preserving the signal that varies drastically such as a speech signal. The filter design is simple and it can
effectively reduce noise. It can reduce not only small stationary noise but also large nonstationary noise.
However, it has some parameters and we need to set them appropriately based on empirical control. So far,
there are few studies to evaluate the appropriateness of the parameter setting of ε-filter in general. In this
paper, we employ correlation coefficient of the filter output and the difference between the input and the filter
output as the evaluation function of the parameter setting. We also show the algorithm to set the optimal
parameter of TF ε-filter. We conducted the experiments to compare the value of the correlation coefficient
and the mean square error when we change ε value. The experimental results show the applicability of our
criterion in parameter setting of ε-filter.
1 INTRODUCTION
Noise reduction plays an important role in speech
recognition and individual identification. When
we consider the instruments like hearing-aids and
phones, noise reduction for a single-channel signal
is required. The spectral subtraction (SS) is a well-
known approach for reducing the noise signal of the
monaural-sound (Boll, 1979; Lim, 1978). It can re-
duce the noise effectively despite of the simple pro-
cedure. However, it can handle only the station-
ary noise. It also needs to estimate the noise in ad-
vance. Although noise reduction utilizing Kalman fil-
ter has also been reported (Kalman, 1960; Fujimoto
and Ariki, 2002), the calculation cost is large. Some
authors have reported a model based approach for
noise reduction (Daniel et al., 2006). In this approach,
we can extract the objective sound by constructing the
sound model in advance. However, it is not applicable
to the signals with the unknown noise as well as SS.
There are some approaches utilizing comb filter (Lim
et al., 1978). In this approach, we firstly estimate the
pitch of the speech signal, and reduce the noise signal
utilizing comb filter. However, the estimation error
results in the degradation of the speech quality.
Some authors have reported a nonlinear filter
named ε-filter for noise reduction (Harashima et al.,
1982) with preserving the signal. We call it “TD ε-
filter” as it treats signal shape in time domain. TD
ε-filter is simple and has some desirable features for
noise reduction. It does not require the model not only
of the signal but also of the noise in advance. It is
easy to be designed and the calculation cost is small.
It can reduce not only the stationary noise but also the
nonstationary noise. However, it can reduce only the
small amplitude noise in principle. To solve the prob-
lems, the method labeled time-frequency ε-filter (TF
ε-filter) was proposed (Abe et al., 2007). TF ε-filter
is an improved ε-filter applied to the complex spec-
tra along the time axis in time-frequency domain. By
utilizing TF ε-filter, we can reduce not only small am-
plitude stationary noise but also large amplitude non-
stationary noise. However, TF ε-filter has some pa-
rameters and we need to set them adequately based
107
Abe T., Matsumoto M. and Hashimoto S. (2009).
PARAMETER OPTIMIZATION IN TIME-FREQUENCY -FILTER BASED ON CORRELATION COEFFICIENT.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 107-111
DOI: 10.5220/0002182601070111
Copyright
c
SciTePress

on empirical control. Moreover, as we only have a
single-channel noisy signal, it is difficult to evaluate
whether the parameter is optimal or not. We cannot
know the difference between the original signal and
the filter output from the observed signal. So far, there
are few studies on the appropriateness of the parame-
ter setting of ε-filter in general.
As a simple criterion, we assume that the signal
and noise are noncorrelated. And we employ the cor-
relation coefficient of the filter output and the differ-
ence between the input signal and the filter output
to set ε adequately. We introduce a method to de-
termine the parameter utilizing the correlation coeffi-
cient. When we utilize the proposed method, we can
set the parameters adequately without the information
about the noise and the signal. In Sec.2, we explain
TF ε-filter to clarify the problem. In Sec.3, we de-
scribe the algorithm of the method to determine the
parameter adequately. In Sec.4, we show the exper-
imental results. Experimental results show that the
proposed method can estimate the optimal parameter
of the TF ε-filter. Conclusions are given in Sec.5.
2 TIME-FREQUENCY ε-FILTER
To clarify the problems of a TF ε-filter, we briefly
explain the TF ε-filter algorithm. TF ε-filter utilizes
the distribution difference of the speech signal and
the noise in the frequency domain. The following as-
sumptions regarding the sound sources are used (Abe
et al., 2007):
• Assumption 1. Speech signal has greater vari-
ation in power than noise signal in the time-
frequency domain.
• Assumption 2. Noise signal is distributed more
uniformly and becomes less variation in the time-
frequency domain compared to in the time do-
main.
Figure 1 depicts the speech signal and the white noise
signal in the time and the time-frequency domains.
As shown in Figure 1, assumptions 1 and 2 are
fulfilled in the case of various noises like white noise
and natural noise such as the sound of a cooling fan.
In Figures 1(b) and (d), the power is normalized based
on the maximal power of the speech signal. When
we consider frequencybins correspondingto the pres-
ence of active speech signal, the power of the noise
with respect to the power of the signal is smaller than
the power of the noise with respect to the power of
the signal in the time domain. In TF ε-filter, we uti-
lize this feature to apply an ε-filter to high-level noise.
0 1 2
-0.4
-0.2
0
0.2
0.4
Time[s]
Amplitude
(a) Speech signal
(in time domain)
Time[s]
Power
1
0.5
0
2
1
0
0
1
2
x 10
4
Frequency[Hz]
(b)Speech signal (in
time-frequency domain)
0 1 2
-0.4
-0.2
0
0.2
0.4
Time[s]
Amplitude
(c) Noise signal
(in time domain)
Power
Frequency[Hz]
Time[s]
1
0.5
0
2
1
0
0
1
2
x 10
(d) Noise signal
(in time-frequency domain)
Figure 1: A speech signal or noise signal in the time and
time-frequency domains.
Let us define x(k) as the input signal sampled at
time k. In TF ε-filter, we firstly transform the input
signal x(k) to the complex amplitude X(κ, ω) by short
term Fourier transformation (STFT). where κ and ω
represent the time frame in the time-frequency do-
main and the angular frequency, respectively. κ and ω
are discrete numbers. Next we execute a TF ε-filter,
which is an ε-filter applying to complex spectra along
the time axis in the time-frequency domain. In this
procedure, Y(κ, ω) is obtained as follows:
Y(κ, ω) =
Q
∑
i=−Q
a(i)X
′
(κ+ i, ω), (1)
where the window size of ε-filter is 2Q+ 1,
X
′
(κ+ i, ω) (2)
=
X(κ, ω) (||X(κ, ω)| − |X(κ+i, ω)|| > ε)
X(κ +i, ω) (||X(κ, ω)| − |X(κ+i, ω)|| ≤ ε),
and ε is a constant.
Figure 2 illustrates the differences in performance
when we apply a TF ε-filter to the speech signal and
the noise. The horizontal axis and the vertical axis
represent the real axis and the imaginary axis, respec-
tively. In the following explanations, we basically use
the word “signal” when we handle them as the sym-
bols while we use the word “complex spectra” when
we handle them as the values. We used the word “sig-
nal” as the mean of “all the signal points”. We also
used the word “complex spectra of the points” as the
“all the complex amplitudes of the points”. In Fig-
ure 2, ∗ and × represent the processed point and the
other signal points in the same window, respectively.
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
108
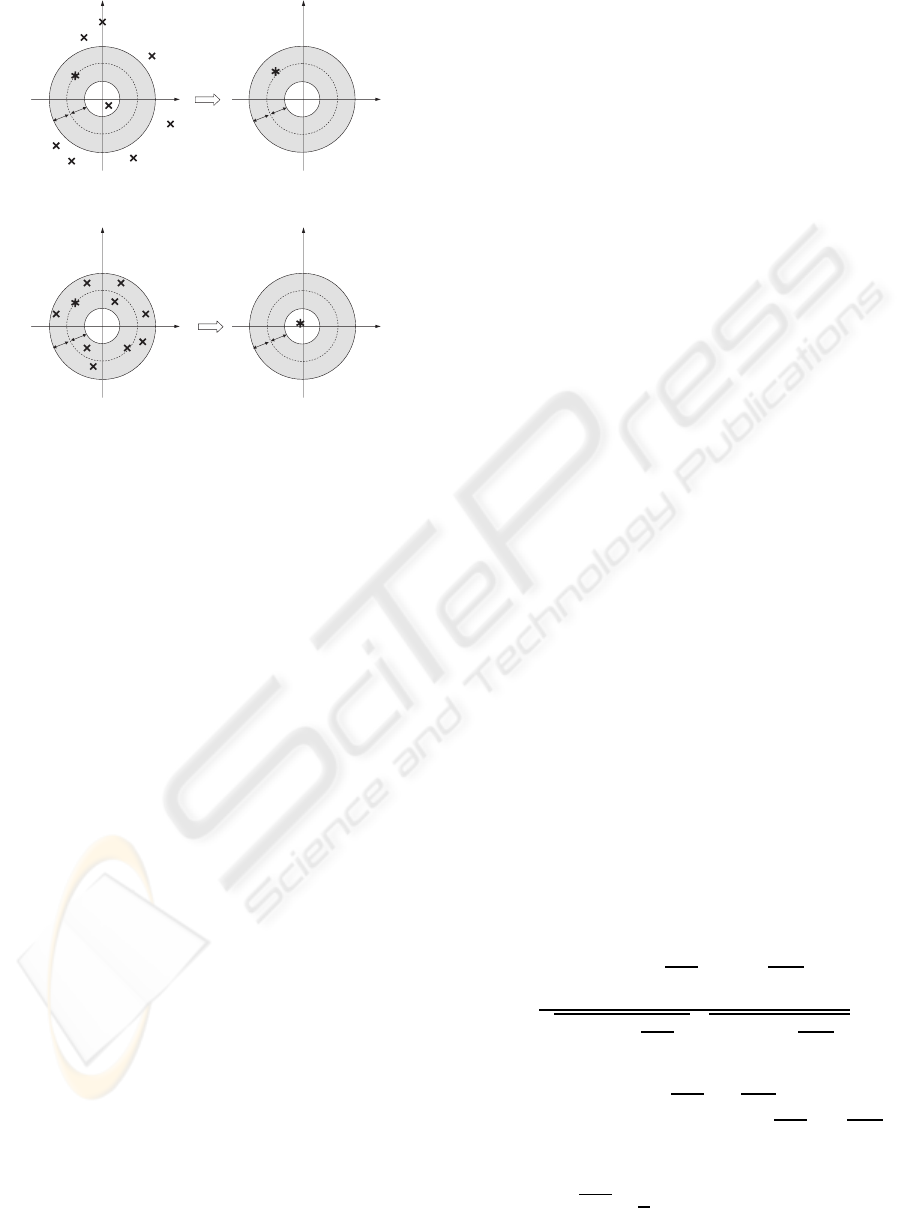
Re
Im Im
Re
A
A'
ε
ε
ε
ε
(a) Speech signal
Im
Re
Im
Re
B'
B
ε
ε
ε
ε
(b) Noise signal
Figure 2: Performance difference when a TF ε-filter is ap-
plied to the speech signal and noise.
Point A in Figure 2(a) and point B in Figure 2(b) rep-
resent the complex amplitude of the processed point.
A
′
and B
′
represent the complex amplitudes of the out-
puts when we apply the TF ε-filter to the points A and
B, respectively. Executing the TF ε-filter, we firstly
replace the complex amplitude of the signal outside
of the shadow area by that of A. We then summate
the complex spectra of all the points in the same win-
dow. Due to handling complex spectra, when we
have many signals that have similar powers but dif-
ferent phases, they are filtered out by the TF ε-filter
and the complex amplitudes of the filter outputs be-
come small. Figure 2(a) represents the basic concept
in the case that the power varies frequently like in
a speech signal. When we consider a signal whose
power varies frequently, the difference between the
absolute value of A and that of the other signals is
large as shown in Figure 2(a). For this reason, many
signals in the same window as the point A are replaced
by A. As a result, when we handle the speech signal,
the complex amplitude of the processed point is al-
most preserved. Figure 2(b) represents the basic con-
cept in case that the power does not vary so much like
in a noise signal. When we consider a noise signal,
the difference between the absolute value of B and
that of the other signals is relatively small compared
with the speech signal. Hence, few signals in the same
window as point B are replaced by B. Based on these
aspects, we can reduce noise while preserving the sig-
nal by setting ε appropriately. Hence, the TF ε-filter
is effective even when the power of the noise with re-
spect to the power of the signal is large. Additionally,
under assumption 2, the TF ε-filter becomes more ef-
fective. When assumption 2 is satisfied, the variation
of the noise with respect to the variation of the sig-
nal in the frequency domain becomes smaller than the
case in the time domain. As a consequence, even if
the noise varies frequently in the time domain, the ε-
filter can be applied in the time-frequency domain.
Then, we transform Y(κ, ω) to y(k) by inverse
STFT.
In TF ε-filter, ε is an essential parameter to reduce
the noise appropriately. If ε is set to excessively large
values, the TF ε-filter becomes similar to linear filter
and smoothes not only the noise but also the signal.
On the other hand, if ε is set to an excessively small
value, it does nothing to reduce the noise anymore.
Due to these reasons, ε value should be set adequately.
3 PARAMETER OPTIMIZATION
UTILIZING CORRELATION
COEFFICIENT
As described in the previous section, when the TF ε-
filter is employed, we need to set ε value adequately
to reduce the noise. However, we cannot estimate op-
timal parameter because the noise and signal are not
known throughout all the procedures.
To solve the problem, we pay attention to the cor-
relation of the speech signal and the noise signal. We
make the following assumption concerning the sound
source and noise:
• Assumption 1. The speech signal is noncorre-
lated with the noise signal.
Let us define s(k) and n(k) as the objective signal
and the noise, respectively. Let R(s(k), n(k)) be the
correlation coefficient of s(k) and n(k) described as
follows:
R(s(k), n(k))
=
L
∑
k=1
(s(k) −
s(k))(n(k) − n(k))
s
L
∑
k=1
(s(k) −
s(k))
2
s
L
∑
k=1
(n(k) −
n(k))
2
, (3)
where L is the data length.
s(k) and n(k) represent the
average of s(k) and n(k), respectively. s(k) and n(k)
are described as follows:
s(k) =
1
L
L
∑
k=1
s(k). (4)
PARAMETER OPTIMIZATION IN TIME-FREQUENCY W-FILTER BASED ON CORRELATION COEFFICIENT
109

n(k) =
1
L
L
∑
k=1
n(k). (5)
When L is large enough, it is expected that the as-
sumption 1 satisfies:
R(s(k), n(k)) = 0. (6)
As described above, s(k) and n(k) are unknown
throughout the filtering procedures. Instead of s(k)
and n(k), we consider the correlation coefficient of
the filter output and the difference between the input
signal and the filter output. Let us consider x(k) and
y(k) as the input signal and the output signal of TF ε-
filter, respectively. x(k) can be described as follows:
x(k) = s(k) + n(k). (7)
When the TF ε-filter can reduce the whole noise,
while it preserves the signal completely, the filter out-
put y(k) equals the signal s(k). The noise n(k) can be
described as follows:
n(k) = x(k) − s(k)
= x(k) − y(k). (8)
Although actual TF ε-filter does not reduce the
whole noise and also reduces the signal, if ε value
is set optimally, it is expected that the correlation co-
efficient of y(k) and x(k) − y(k), R(y(k), x(k) − y(k))
has a smaller value than R(y(k), x(k) − y(k)) in other
ε. Hence, the optimal parameter ε
opt
can be obtained
as
ε
opt
= argmin
ε
R(y(k), x(k) − y(k)), (9)
where
R(y(k), x(k) − y(k)) (10)
=
L
∑
k=1
(y(k) −
y(k))(x(k) − y(k) − x(k) − y(k))
s
L
∑
k=1
(y(k) −
y(k))
2
s
L
∑
k=1
(x(k) − y(k) −
x(k) − y(k))
2
,
where
x(k) and x(k) − y(k) represent the aver-
age of x(k) and x(k) − y(k), respectively. x(k) and
x(k) − y(k) are described as follows:
x(k) =
1
L
L
∑
k=1
x(k). (11)
x(k) − y(k) =
1
L
L
∑
k=1
(x(k) − y(k)). (12)
We test its adequateness in the following section.
0 1 2
-0.4
-0.2
0
0.2
0.4
Time[s]
Amplitude
Figure 3: Waveform of the nonstationary noise.
4 EXPERIMENT
4.1 Experimental Condition
To clarify the adequateness of the proposed method,
we conducted the experiments utilizing a speech sig-
nal with a noise signal. In the experiments, we cal-
culate R(y(k), x(k) − y(k)) and the mean square error
(MSE) between the original signal s(k) and the filter
output y(k). MSE is defined as follows:
MSE =
1
L
L
∑
k=1
(s(k) − y(k))
2
. (13)
As the sound source, we used “Japanese Newspa-
per Article Sentences” edited by the Acoustical Soci-
ety of Japan. We used the white noise with uniform
distribution as the stationary noise. As nonstation-
ary noise, we prepared white noise with the ampli-
tude that sometimes varied as shown in Figure 3. The
signal and the noise are mixed in the computer. The
sampling frequency and quantization bit rate are set at
44.1kHz and 16bits, respectively. We set the window
size of TF ε-filter at 61.
4.2 Relation between the MSE and the
Correlation Coefficient
We prepared two noisy signals with stationary noise
and nonstationary noise whose SNR are 10.0[dB]. We
applied the ε-filter to the signals with changingε value
with range[0.1, 0.5].
Figures 4 and 5 show the experimental results
when we use the signal with stationary noise and non-
stationary noise as the input signal, respectively. As
shown in Figures 4 and 5, the ε value that has the
minimal value of correlation coefficient corresponds
to the ε value that has the minimal value of MSE in
both cases. We could obtain similar results when we
utilized other signals.
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
110
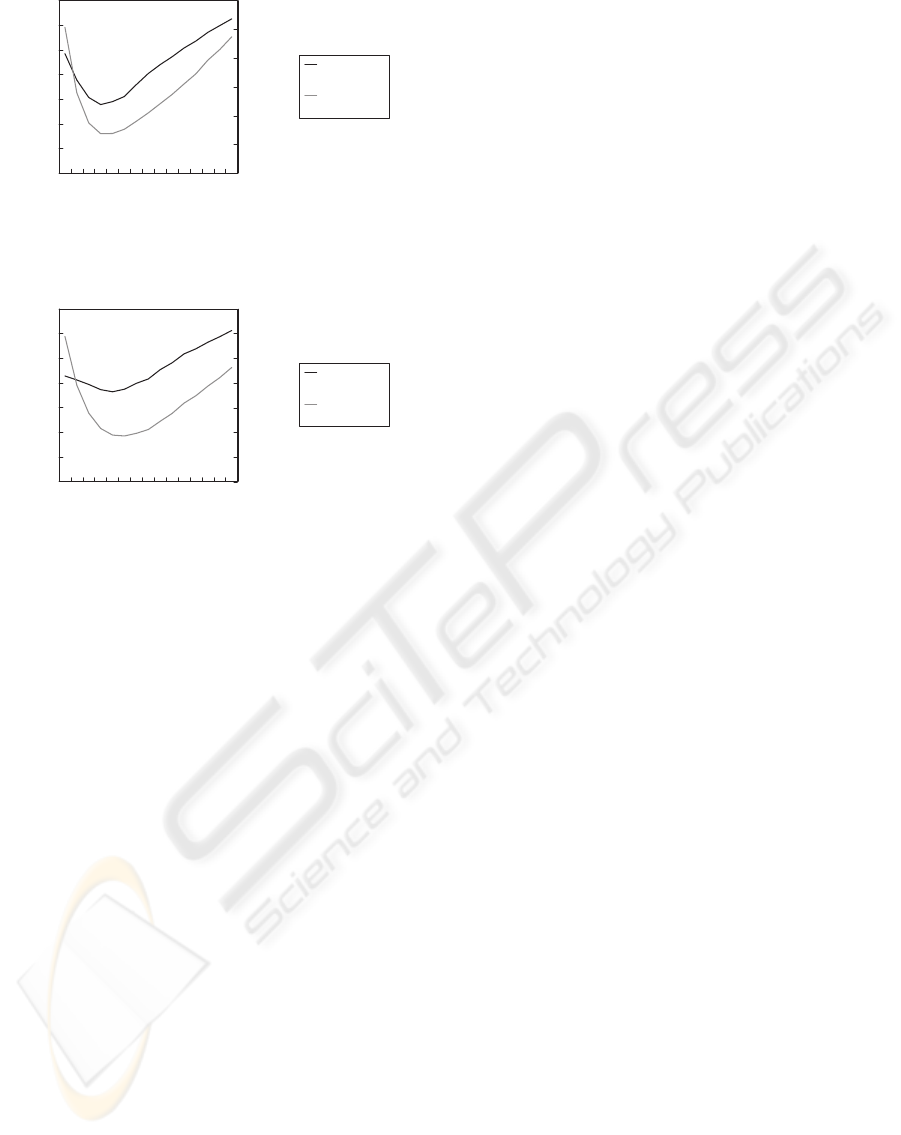
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.1 0.3 0.5 0.7 0.9 1.1 1.3 1.5
ε
Correlation coefficient
0
0.05
0.1
0.15
0.2
0.25
0.3
Mean square error[x10 ]
Correlation
coefficient
Mean square
error
-3
Figure 4: Experimental result when we used the signal with
stationary noise.
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.1 0.3 0.5 0.7 0.9 1.1 1.3 1.5
ε
Correlation coefficient
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
Mean square error[x10 ]
Correlation
coefficient
Mean square
error
-3
Figure 5: Experimental result when we used the signal with
nonstationary noise.
5 CONCLUSIONS
In this paper, we employed correlation coefficient of
the filter output and the difference between the input
and the filter output as the evaluation function of the
parameter setting of TF ε-filter. We also introduced
an algorithm to determine the parameter of TF ε-filter
automatically. The experimental results showed that
we can determine the parameter of TF ε-filter ade-
quately by utilizing our criterion. We can employ
ε value which has the minimal value of correlation
coefficient between x(k) and x(k) − y(k) when TF ε-
filter is used. As the proposed method only assumes
the decorrelation of the signal and noise, it is expected
that the application range of the proposed method
is wide. By using our method, even when we only
have the single-channel noisy signal, we can evaluate
whether the ε value is adequate or not. The proposed
method does not require to estimate the noise in ad-
vance. For future works, we would like to evaluate the
robustness for changing the window size of the TF ε-
filter. We also would like to determine all parameters,
that is, not only the ε value but also the window size
adequately based on automatic control. Adaptive TF
ε-filter, which can change its parameter adaptively de-
pending on the input signal, will be developed in the
near future.
ACKNOWLEDGEMENTS
This research was supported by the research grant
of Support Center for Advanced Telecommunications
Technology Research (SCAT), by the research grant
of Foundation for the Fusion of Science and Tech-
nology, and by the Ministry of Education, Culture,
Sports, Science and Technology, Grant-in-Aid for
Young Scientists (B), 20700168, 2008. This research
was also supported by the CREST project ”Founda-
tion of technology supporting the creation of digi-
tal media contents” of JST, by the Grant-in-Aid for
the WABOT-HOUSE Project by Gifu Prefecture, and
the Global-COE Program,” Global Robot Academia”,
Waseda University.
REFERENCES
Abe, T., Matsumoto, M., and Hashimoto, S. (2007). Noise
reduction combining time-domain ε-filter and time-
frequency ε-filter. In J. of the Acoust. Soc. America.,
volume 122, pages 2697–2705.
Boll, S. F. (1979). Suppression of acoustic noise in speech
using spectral subtraction. In IEEE Trans. Acoust.
Speech Signal Process., volume ASSP-27, pages 113–
120.
Daniel, P., Ellis, W., and Weiss., R. (2006). Model-based
monaural source separation using a vector-quantized
phase-vocoder representation. In Proc. IEEE Int’l
Conf. on Acoustics, Speech, and Signal Process. 2006.
Fujimoto, M. and Ariki, Y. (2002). Speech recognition un-
der noisy environments using speech signal estimation
method based on kalman filter. In IEICE Trans. Infor-
mation and Systems, volume J85-D-II, pages 1–11.
Harashima, H., Odajima, K., Shishikui, Y., and Miyakawa,
H. (1982). ε-separating nonlinear digital filter and its
applications. In IEICE trans on Fundamentals., vol-
ume J65-A, pages 297–303.
Kalman, R. E. (1960). A new approach to linear filtering
and prediction problems. In Trans. of the ASME, vol-
ume 82, pages 35–45.
Lim, J. S. (1978). Evaluation of a correlation subtraction
method for enhancing speech degraded by additive
white noise. In IEEE Trans. Acoust. Speech Signal
Process., volume ASSP-26, pages 471–472.
Lim, J. S., Oppenheim, A. V., and Braida, L. (1978). Eval-
uation of an adaptive comb filtering method for en-
hancing speech degraded by white noise addition. In
IEEE Trans. on Acoust. Speech Signal Process., vol-
ume ASSP-26, pages 419–423.
PARAMETER OPTIMIZATION IN TIME-FREQUENCY W-FILTER BASED ON CORRELATION COEFFICIENT
111
