NOISE REDUCTION BASED ON MEDIAN ε- FILTER

Mitsuharu Matsumoto

The Education and Research Center for Frontier Science, The University of Electro-communications

1-5-1, Chofugaoka, Chofu-shi, Tokyo, 182-8585, Japan

Keywords:

Noise reduction, Median ε-ﬁlter, ε-ﬁlter, Impulse noise.

Abstract:

This paper describes a nonlinear ﬁlter, which can reduce the impulse noise with preserving the edge infor-

mation labeled median ε-ﬁlter. ε-ﬁlter is a nonlinear ﬁlter, which can reduce the small amplitude noise with

preserving the edge information. The algorithm is simple and it has many applications because it uses only

switching and linear operations. Although it is difﬁcult to reduce the impulse noise by using ε-ﬁlter due to its

features, we can reduce the impulse noise effectively with preserving the edge information by combining the

concept of median ﬁlter and ε-ﬁlter. Due to its simple design, the calculation cost is relatively small the same

as ε-ﬁlter. To show the effectiveness of the proposed method, we also report the results of some comparative

experiments concerning the ﬁlter characteristics.

1 INTRODUCTION

Noise reduction has an important role in image pro-

cessing. Although there are many kinds of noise to be

reduced, impulse noise reduction is one of the impor-

tant topics because it appears in many practical cases

due to errors generated in noisy sensors or commu-

nication channels. Although there are many studies

to reduce the impulse type noise (Pitas and Venet-

sanopoulos, 1990), median ﬁlter is an attractive ﬁl-

ter to reduce the impulse noise (Ko and Lee, 1991;

Brownrigg, 1984; Lin and Willson, 1988). It is simple

and effectively reduces the impulse noise. However,

as median ﬁlter smooths not only the pixels which in-

clude impulse noise but also the undistorted pixels, it

damages the good pixels.

Some researches aim to avoid the damages to the

image by combining the impulse detector and median

ﬁlter (Abreu et al., 1996; Wang and Zhang, 1999; Sun

and Neuvo, 1994; Wang and Zhang, 1998; Muneyasu

et al., 2000; Yamashita et al., 2006). Although these

approaches generally work well, the estimation error

degrades the ﬁlter performance. As these ﬁlters also

employ the learning algorithms or detecting process,

it requires much calculation cost compared to the sim-

ple median ﬁlter. They also need the noise free image

for learning.

To solve the problem, we look to a nonlinear ﬁl-

ter labeled ε-ﬁlter (Harashima et al., 1982; Arakawa

et al., 2002; Arakawa and Okada, 2005). ε-ﬁlter is

a nonlinear ﬁlter, which can reduce the small ampli-

tude noise with preserving the edge the same as the

bilateral ﬁlter (Tomasi and Manduchi, 1998). The

algorithm is simple and the calculation cost is small

compared to bilateral ﬁlter because it requires only

switching and linear operation. Although it is difﬁ-

cult to reduce the impulse noise by using ε-ﬁlter due

to its design, the concept of ε-ﬁlter can be expanded

to design the improved median ﬁlter. Based on the

aspects, we propose a nonlinear ﬁlter combining the

concepts of ε-ﬁlter and median ﬁlter labeled median

ε-ﬁlter. The algorithm is simple and it can effectively

reduce the impulse noise. As it does not employ the

impulse detector, it does not require the noise free im-

age or learning process. In the next section, we ﬁrst

describe the algorithm of the conventional ε-ﬁlter to

clarify its feature. In Sec.3, we describe the algorithm

of the median ε-ﬁlter. In Sec.4, we show our exper-

imental results of evaluating the ﬁlter characteristics

of median ε-ﬁlter. We also compare the ﬁlter perfor-

mance with some other ﬁlters. Conclusions follow in

Sec.5.

2 ε-FILTER

We ﬁrstly explain the algorithm of ε-ﬁlter. To clar-

ify the feature of ε-ﬁlter, we ﬁrst describe the one di-

mensional case. Let us deﬁne x(k) as the input signal

(For instance, the signal including speech signal with

112

Matsumoto M. (2009).

NOISE REDUCTION BASED ON MEDIAN -FILTER.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 112-117

DOI: 10.5220/0002182701120117

 SciTePress

(a) Input signal

(b) In the case of ap-

plying ε-ﬁlter to the

point A

plying ε-ﬁlter to the

point B

Figure 1: Basic concept of ε-ﬁlter.

noise) at time k. Let us also deﬁne y(k) as output sig-

nal of ε-ﬁlter at time k as follows:

y(k) = x(k) +

∑

i=−M

a(i)F(x(k+ i) − x(k)), (1)

where a(i) represents the ﬁlter coefﬁcient. a(i) is usu-

ally constrained as follows:

∑

i=−M

a(i) = 1. (2)

The window size of ε-ﬁlter is 2M + 1. F(x) is the

nonlinear function described as follows:

|F(x)| ≤ ε : −∞ ≤ x ≤ ∞, (3)

where ε is the constant number. This method can re-

duce small amplitude noise while preserving the sig-

nal. For example, we can set the nonlinear function

F(x) as follows:

F(x) =



x (−ε ≤ x ≤ ε)

0 (else)

. (4)

Figure 1 shows the basic concept of ε-ﬁlter in case

that we utilize Eq.4 as F(x). Fig.1(a) shows the wave-

form of the input signal. Executing ε-ﬁlter at the point

A in Fig.1(a), we replace all the points whose differ-

ence from A is larger than ε by the value of the point

A. We then summate the signals in the same window.

Fig.1(b) shows the basic concept of this procedure. In

Fig.1(b), the dotted line represents the points whose

difference from A is larger than ε. In Fig.1(b), the

solid line represents the values replaced through this

procedure. As a result, if the difference between the

point A and the other point is large, the point is ig-

nored. On the other hand, if the difference between

the point A and the other point is small, the point is

smoothed. Because of this procedure, ε-ﬁlter reduces

the noise with preserving the precipitous attack and

decay of the speech signal, In the same way, execut-

ing ε-ﬁlter at the point B in Fig.1(a), we replace all

the points whose difference from B is larger than ε

by the value of the point B. The point is ignored

if the difference from the point B is large, while the

point is smoothed if the difference from the point B is

small. Consequently, we can reduce the small ampli-

tude noise near by the processed point while preserv-

ing the speech signal.

ε-ﬁlter can easily be improvednot only for one dimen-

sion but also for two dimension. Let us deﬁne x(k, l)

as the two dimensional input signal at (k, l). When we

apply ε-ﬁlter to two dimensional data such as image,

ε-ﬁlter is designed as follows:

y(k, l) = x(k, l) (5)

∑

i=−M

∑

j=−M

a(i, j)F(x(k+ i, l + j) − x(k, l)),

where a(i, j) represents the ﬁlter coefﬁcient. a(i, j)

is usually constrained as follows:

∑

i=−M

∑

j=−M

a(i, j) = 1. (6)

The feature of two dimensional ε-ﬁlter is similar to

that of one dimensional ε-ﬁlter. We can smooth the

small amplitude noise near by the processed point

while preserving the edge. It requires less calculation

when it is compared to bilateral ﬁlter because it re-

quires only switching and linear operation. However,

it is difﬁcult to reduce the impulse noise because of

its feature.

3 MEDIAN ε-FILTER

To reduce the impulse noise with preserving the edge

information, we combine the concept of median ﬁl-

ter and ε-ﬁlter. In median ﬁlter, we set the adequate

window and replace the ﬁltered point to the median

value in the window. The median ﬁlter can reduce

the impulse noise. However, the edge information is

sometimes damaged. To solve the problems, median

ε-ﬁlter is designed as follows:

y(k) = med

i=−M

[v(k+ i)], (7)

where med

i=−M

[v(k+ i)] represents the median func-

tion of v(k) from v(k − M) to v(k + M). v(k + i) is

described as follows:

v(k+ i) = x(k+ i) + F(x(k) − x(k+ i)), (8)

where F(x) is the same nonlinear function as Eq.(3)

constrained as follows:

|F(x)| ≤ ε : −∞ ≤ x ≤ ∞, (9)

NOISE REDUCTION BASED ON MEDIAN W-FILTER

113

Impulse noise

(a) Input signal

Impulse noise

Window size

(b) In the case of ap-

plying median ε-ﬁlter

to the point A

Impulse noise

Window size

plying median ε-ﬁlter

to the point B

Impulse noise

Window size

(d) In the case of ap-

plying median ε-ﬁlter

to the point C

Figure 2: Basic concept of median ε-ﬁlter.

where ε is the constant number. For example, we can

set the nonlinear function F(x) similar to ε-ﬁlter as

follows:

F(x) =



x (−ε ≤ x ≤ ε)

0 (else)

. (10)

In this case, the output of median ε-ﬁlter can be de-

scribed as:

y(k) = med

i=−M

[v(k+ i)], (11)

where

v(k+ i) =



x(k) (|x(k + i) − x(k)| ≤ ε)

x(k+ i) (|x(k+ i) − x(k)| > ε)

(12)

Figure 2 shows the basic concept of median ε-ﬁlter in

case that we utilize Eq.(10) as F(x). Fig.2(a) shows

the waveform of the input signal. Executing ε-ﬁlter

at the point A in Fig.2(a), we replace all the points

where the difference from A is smaller than ε by the

value of the point A. We then apply the median ﬁl-

ter to the signals in the same window. Fig.2(b) shows

the basic concept of this procedure. In Fig.2(b), the

dotted line represents the points where the difference

from A is smaller than ε. In Fig.2(b), the solid line

represents the values replaced through this procedure.

As the median ﬁlter outputs the median value in the

window, the input signal is basically intact when there

are many signals in the window within ε as shown in

Fig.2(b). In a similar fashion, executing ε-ﬁlter at the

point B in Fig.2(a), we replace all the points where

the difference from B is smaller than ε by the value

of the point B. In this case, although the point C is

(a) Original image of Lena. (b) Original image with

noise.

Figure 3: Original image (Lena) and input image with im-

pulse noise.

included in the window, as there are also many sig-

nals in the window within ε, the input signal is also

intact. Executing ε-ﬁlter at the pointC (Impulse noise

point) in Fig.2(a), as the differences between the point

C and the other points are larger than ε in the window,

the points within the same window are not replaced.

Hence, at the point C, median ε-ﬁlter works as a sim-

ple median ﬁlter and reduces this impulse noise. Due

to the above features, the median ε-ﬁlter can reduce

the impulse noise without damaging the good pixels.

To improve median ε-ﬁlter for two dimensional data,

we only have to design it as follows:

y(k, l) = med

M,M

i=−M, j=− M

[v(k+ i, l + j)], (13)

where

v(k+ i, l + j) = x(k + i, l + j) + F(x(k, l)−x(k+ i, l + j)).

(14)

The feature of two dimensional median ε-ﬁlter is sim-

ilar to that of one dimensional median ε-ﬁlter. The

calculation cost of median ε-ﬁlter is small the same

as ε-ﬁlter because it requires only the switching and

replacing operation. We can also reduce both im-

pulse noise and small amplitude noise with preserv-

ing edge information by combining the conventional

ε-ﬁlter and median ε-ﬁlter.

4 EXPERIMENTS

To show the effectiveness of the proposed method, we

ﬁrst show the output images after the ﬁltering. As

examples, we show the results using Lena and Boat

listed in standard image database (SIDBA). To com-

pare the effectiveness of the proposed methods to the

other methods, we also show the ﬁlter outputs of the

simple median ﬁlter and progressive switching me-

dian ﬁlter (PSMF) (Wang and Zhang, 1999). In the

experiments, we set the window size to 5 pixels ×

5 pixels. Figure 3 and Figure 5 show the examples

of Lena and Boat, respectively. They show the orig-

inal images and the input images with impulse noise

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications

114

(a) Output image of me-

dian ﬁlter.

(b) Output image of pro-

gressive switching median

ﬁlter.

dian ε-ﬁlter.

Figure 4: Filter outputs using Lena.

(a) Original image of Boat. (b) Original image with

noise.

Figure 5: Original image (Boat) and input image with im-

pulse noise.

whose noise level is 10%, i.e. 10% pixels of the im-

age are added the impulse noise. Figure 4 and Figure

6 show the ﬁlter outputs of the simple median ﬁlter,

PSMF and the median ε-ﬁlter concerning Lena and

Boat, respectively. As shown in Figs.4(a) and 6(a),

when we employed the simple median ﬁlter, as all the

pixels were ﬁltered, the edge information was also

damaged. When we employed the PSMF, although

the edge was preserved compared to the simple me-

dian ﬁlter, some impulse noises remained due to the

estimation error as shown in Figs.4(b) and 6(b). On

the other hand, the median ε-ﬁlter could reduce the

impulse noise without damaging the original image

information.

To clarify the effectiveness of the proposed method,

we also calculated the mean absolute error (MAE). In

the experiments, we used ten images listed in SIDBA

(a) Output image of me-

dian ﬁlter.

(b) Output image of pro-

gressive switching median

ﬁlter.

dian ε-ﬁlter.

Figure 6: Filter outputs using Boat.

Mean absolute error (MAE)

5% 10% 15% 20%

Noise level

MAE

Noisy

Median

PSMF

Proposed

Figure 7: Mean absolute error of input signal, median ﬁlter

and median ε-ﬁlter with changing the noise level from 5%

to 20%.

and changed the noise level from 5% to 20% with

5% interval. Tables 1, 2, 3, and 4 show the MAE

results when we used the input image with the im-

pulse noise whose noise level was 5%, 10%, 15% and

20%, respectively. To clarify the effectiveness of the

proposed method compared to the other methods, we

also show the average MAE. Figure 7 shows the av-

erage MAEs of input signal, median ﬁlter, PSMF and

median ε-ﬁlter. As shown in Fig.7, the MAE values

of the proposed ﬁlter are much smaller than those of

median ﬁlter in all the cases in spite of its simple de-

sign.

NOISE REDUCTION BASED ON MEDIAN W-FILTER

115

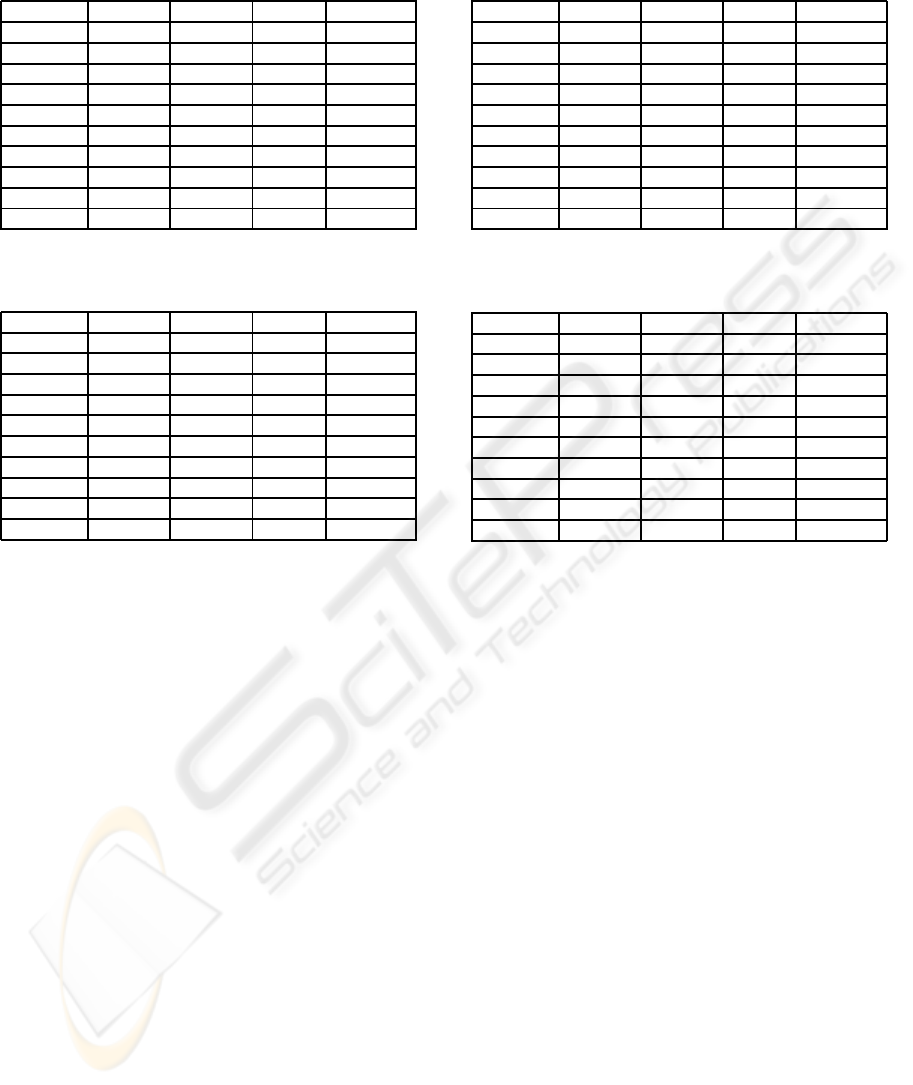
Table 1: MAE results when we added impulse noise whose

noise level is 5%.

Noisy Median PSMF Proposed

Lena 12.1282 3.9409 0.7034 0.2803

Mandrill 12.2644 12.1395 4.7043 0.6881

Airplane 12.4084 5.9639 1.8183 0.4003

Barbara 12.3033 12.4223 4.8263 0.7331

Boat 11.922 4.7659 1.0482 0.2938

Bridge 12.3889 13.1145 4.7397 0.749

Building 12.0309 7.5519 1.4239 0.453

Girl 12.3734 4.0123 0.4649 0.2812

Lax 12.5095 12.1752 5.5711 0.8165

Woman 12.3111 5.2059 1.1797 0.364

Table 2: MAE results when we added impulse noise whose

noise level is 10%.

Noisy Median PSMF Proposed

Lena 24.6922 4.3668 1.1233 0.5985

Mandrill 24.0891 12.474 5.1548 1.388

Airplane 24.4821 6.444 2.4129 0.8411

Barbara 24.3965 12.7899 5.4746 1.4835

Boat 24.2603 5.1177 1.5635 0.6371

Bridge 24.7934 13.5914 5.6281 1.6209

Building 24.6961 8.0907 1.9957 1.0329

Girl 24.8829 4.4298 0.8757 0.5783

Lax 24.4549 12.4003 5.9064 1.4839

Woman 24.0269 5.5859 1.7034 0.7206

5 CONCLUSIONS

In this paper, we proposed a nonlinear ﬁlter which can

reduce the impulse noise with preserving the image

information labeled median ε-ﬁlter. The proposed ﬁl-

ter is simple and can reduce the noise effectively com-

pared to the simple median ﬁlter or more complicated

median ﬁlters. It does not require the noise free image

or learning process. For future works, we would like

to employ the median ε-ﬁlter for musical noise reduc-

tion by applying it to the acoustical signal in time-

frequency domain.

ACKNOWLEDGEMENTS

This research was supported by the research grant

of Support Center for Advanced Telecommunications

Technology Research (SCAT), by the research grant

of Foundation for the Fusion of Science and Tech-

nology, by the research grant of Tateisi Science and

Technology Foundation, and by the Ministry of Edu-

cation, Science, Sports and Culture, Grant-in-Aid for

Young Scientists (B), 20700168, 2008.

Table 3: MAE results when we added impulse noise whose

noise level is 15%.

Noisy Median PSMF Proposed

Lena 36.7582 4.8799 2.1492 1.006

Mandrill 36.3613 13.052 6.1686 2.2151

Airplane 37.1239 7.1861 3.3719 1.4578

Barbara 37.3263 13.3853 6.7379 2.4936

Boat 36.2212 5.7219 2.5915 1.0588

Bridge 37.1201 14.4864 6.6049 2.666

Building 36.6181 8.849 3.2259 1.6762

Girl 36.6804 4.9845 1.7034 1.0209

Lax 37.0422 13.0186 7.0353 2.3751

Woman 36.5364 6.1773 2.6824 1.1469

Table 4: MAE results when we added impulse noise whose

noise level is 20%.

Noisy Median PSMF Proposed

Lena 49.0226 5.947 4.0882 1.8503

Mandrill 49.2094 14.178 8.5962 3.4303

Airplane 49.2094 8.2621 5.7692 2.3816

Barbara 49.0226 14.3624 8.8842 3.7084

Boat 49.0109 6.637 4.6289 1.8491

Bridge 48.3533 15.9184 9.1091 4.1476

Building 48.4701 9.9992 5.6002 2.7381

Girl 49.0148 5.9428 3.5904 1.7574

Lax 49.0421 14.428 9.3909 3.957

Woman 48.2444 7.2482 4.8524 1.997

REFERENCES

Abreu, E., Lightstone, M., Mitra, S. K., and Arakawa, K.

(1996). A new efﬁcient approach for the removal of

impulse noise from highly corrupted image. In IEEE

Transactions on Image Processing. IEEE.

Arakawa, K., Matsuura, K., Watabe, H., and Arakawa, Y.

(2002). A method of noise reduction for speech sig-

nals using component separating ε-ﬁlters. In IEICE

Transactions on Fundamentals. IEICE.

Arakawa, K. and Okada, T. (2005). ε-separating nonlinear

ﬁlter bank and its application to face image beautiﬁca-

tion. In IEICE Transactions on Fundamentals. IEICE.

Brownrigg, D. R. K. (1984). The weighted median ﬁlter. In

Communications of the ACM. ACM.

Harashima, H., Odajima, K., Shishikui, Y., and Miyakawa,

H. (1982). ε-separating nonlinear digital ﬁlter and its

applications. In IEICE Transactions on Fundamen-

tals. IEICE.

Ko, S.-J. and Lee, Y. H. (1991). Center weighted median

ﬁlters and their application to image enhancement. In

IEEE Transactions on Circuits and Systems. IEEE.

Lin, H. and Willson, A. N. (1988). Median ﬁlter with adap-

tive length. In IEEE Transactions on Circuits and Sys-

tems. IEEE.

Muneyasu, M., Ochiai, T., and Hinamoto, T. (2000). An

implementation for switching median ﬁlters based on

SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications

116

pattern classiﬁcation. In IEICE Transactions on Fun-

damentals. IEICE.

Pitas, I. and Venetsanopoulos, A. N. (1990). Nonlinear dig-

ital ﬁlters: principles and applications. Kluwer Aca-

demic Pub, USA, 1st edition.

Sun, T. and Neuvo, Y. (1994). Detail-preserving median

based ﬁlters in image processing. In Pattern recogni-

tion letters. Elsevier.

Tomasi, C. and Manduchi, R. (1998). Bilateral ﬁltering for

gray and color images. In International Conference

on Computer Vision. IEEE.

Wang, Z. and Zhang, D. (1998). Restoration of impulse

noise corrupted image using long-range correlation. In

IEEE Transactions on Signal Processing. IEEE.

Wang, Z. and Zhang, D. (1999). Progressive switching

median ﬁlter for the removal of impulse noise from

highly corrupted images. In IEEE Transactions on

Circuits and Systems. IEEE.

Yamashita, N., Ogura, M., Lu, J., Sekiya, H., and Yahagi,

T. (2006). A random-valued impulse noise detector

by using level detection. In IEICE Transactions on

Fundamentals. IEICE.

NOISE REDUCTION BASED ON MEDIAN W-FILTER

117