ROBUST AND REVERSIBLE NUMERICAL SET WATERMARKING
Gaurav Gupta, Josef Pieprzyk
Centre for Advanced Computing - Algorithms and Cryptography
Macquarie University, Australia
Mohan Kankanhalli
School of Computing, National University of Singapore
Keywords:
Watermarking, Copyright protection.
Abstract:
Numeric sets can be used to store and distribute important information such as currency exchange rates and
stock forecasts. It is useful to watermark such data for proving ownership in case of illegal distribution by
someone. This paper analyzes the numerical set watermarking model presented by Sion et. al in “On water-
marking numeric sets”, identifies it’s weaknesses, and proposes a novel scheme that overcomes these prob-
lems. One of the weaknesses of Sion’s watermarking scheme is the requirement to have a normally-distributed
set, which is not true for many numeric sets such as forecast figures. Experiments indicate that the scheme is
also susceptible to subset addition and secondary watermarking attacks. The watermarking model we propose
can be used for numeric sets with arbitrary distribution. Theoretical analysis and experimental results show
that the scheme is strongly resilient against sorting, subset selection, subset addition, distortion, and secondary
watermarking attacks.
1 INTRODUCTION
Piracy of digital objects such as audio, video and soft-
ware is becoming a major concern for the owners of
these documents. It is becoming easier for the pirates
to obtain and distribute the data using peer-to-peer
networks and file-sharing hosts and it is getting more
difficult for the owners to prevent this illegal distribu-
tion, in which case it becomes important for the owner
to be able to at least establish his ownership over the
object if a person is found in possession of a digital
object, believed to be pirated. This is accomplished
be watermarking; the process of embedding informa-
tion by introducing small changes in digital data. Suc-
cessful retrieval of this information with a secret key
establishes the ownership of the key-holder over the
concerned object. An effective watermarking scheme
should have the following features:
1. Detectability: The watermark should be de-
tectable in order to establish ownership.
2. Robustness: The watermark should survive at-
tacks such as cropping, data modification, and
more.
3. Low false positives: There should be negligible
possibility of accidentally detecting a watermark
in an unmarked object.
4. Blindness: Only the watermarked object and a se-
cret key should be needed to detect watermark.
5. Imperceptibility: The watermark should have
minimal impact on the quality of data.
Several watermarking schemes have been pro-
posed in the past for images (Cox et al., 1996; Bors
and Pitas, 1996), software (Venkatesan et al., 2001;
Collberg and Thomborson, 1999; Qu and Potkon-
jak, 1998), databases (Sion et al., 2004; Zhang et al.,
2004) and text documents (Bolshakov, 2005; Atallah
et al., 2001), but numerical sets have not been given
the deserved attention, with only two major works
known to the authors (Sion et al., 2002; Sebe et al.,
2005). Numeric sets are extensively useful in several
fields such as weather, military, scientific results and
bio-informatics to name a few. For instance, manage-
ment consulting firms such as McKinsey provide fi-
nancial institutions with valuable data concerningcur-
rency and stock fluctuations. Their clients employ
thousands of employees who have access to this in-
141
Gupta G., Pieprzyk J. and Kankanhalli M. (2009).
ROBUST AND REVERSIBLE NUMERICAL SET WATERMARKING.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 141-148
DOI: 10.5220/0002186901410148
Copyright
c
 SciTePress

formation. The data provider would prefer that the
information is not distributed without it’s permission.
But since this is not always possible, the company at
least should have provable ownership over the data.
The numeric watermarking model proposed in
(Sebe et al., 2005) focuses on preserving the statis-
tical properties of a numerical set, including arith-
metic mean and variance. The scheme has high false
positive rates of up to 30.85%, thereby possibly in-
criminating innocent users and also lacks a substan-
tial analysis of the model’s security against an active
adversary. In this paper, we present a watermarking
scheme for numeric sets that satisfies the desirable
features of a watermarking scheme mentioned above.
1.1 Organization of Paper
In Section 2, we discuss and analyze the numeric set
watermarking scheme from “On watermarking nu-
meric sets” (Sion et al., 2002), present experimen-
tal results demonstrating the weaknesses of the model
and also discuss solutions to eliminate these draw-
backs. In Section 3, we propose a fresh watermarking
model and present the algorithms in Section 3.1. Sec-
tion 4 includes a comprehensive analysis of the pro-
posed model and the experimental results. The paper
is concluded in Section 5 with a note on future re-
search direction.
2 SION’S WATERMARKING
SCHEME (SWS)
This section analyzes SWS that they later extend for
database watermarking (Sion et al., 2004). The wa-
termarking model is based on the statistical distribu-
tions of subsets. The subset partitioning is based on
the most significant bits (MSBs) of set items. Items
of a subset are then modified such that they satisfy
some data usability conditions (DUC), such as maxi-
mum allowable mean square error. When a value s
i
is
changed to v
i
during watermark insertion, the follow-
ing two conditions must be satisfied:
(s
i
− v
i
)
2
< t
i
1 ≤ i ≤ n (1)
∑
((s
i
− v
i
)
2
) < t
max
(2)
where T = {t
i
|1 ≤ i ≤ n,t
i
∈ R} is the set of indi-
vidual bounds and t
max
∈ R is the overall bound.
The authors address subset selection, addition, al-
teration and re-ordering attacks. However, secondary
watermarking or additive attacks, is left out. The de-
tailed watermarking process is as follows:
1. Numeric set to watermark is S = {s
i
|1 ≤ i ≤ n,s
i
∈
R}, k
′
is the private key to generate item indices,
MSB( f, s
i
) are the f MSBs of s
i
, and NORM a
normalization operation.
2. Items are ordered using hashing performed on the
secret key k
′
and the f MSBs of the items’ nor-
malized value using Equation 3, thereby imposing
a secret key-based order on the items.
index(s
i
) = H(k
′
,MSB( f, NORM(s
i
)),k
′
) (3)
3. Create subsets S
i
of equal sizes where,
S
i
= {x
i
j
|x
i
j
= s
i×y+ j
,0 ≤ i <
n
y
,1 ≤ j ≤ y} (4)
Each subset contains y adjacent items from the list
of items sorted by indices (calculated using Equa-
tion 3).
4. The maximum of n/y bits can be embedded in
each subset. Each bit of a b-bit watermark can be
embedded up to n/(y × b) times. This provides
error-correction capabilities.
5. Let avg(S
i
) =
∑
y
j=0
(x
i
j
) and δ(S
i
) =
r
∑
(avg(S
i
)−x
i
j
)
2
y
be the average and standard
deviation of the items of S
i
, respectively. Let
v
true
,v
false
,c ∈ (0,1) be real numbers. The value
c is a confidence factor while (v
true
,v
false
) are
confidence violators such that v
true
> v
false
. As
an example, let c = 0.9,v
true
= 0.1,v
false
= 0.07.
v
c
(S
i
) is the number of items greater than
avg(S
i
) + c× δ(S
i
). Bit encoded in a subset S
i
is
‘1’ if v
c
(S
i
) > v
true
× y, ‘0’ if v
c
(S
i
) < v
false
× y
and otherwise invalid.
Algorithm Please place \label after
\caption embeds a single watermark bit b in
a subset S
i
. If it returns success, we insert the next
bit, otherwise we insert the same bit, in the next
subset. Detection algorithm works symmetrically,
identifying watermarked bit in subsets created from
Equations 3, 4.
The watermarking scheme is presented to be re-
silient against several attacks such as re-sorting (obvi-
ously, the actual sorting that the watermarking algo-
rithm uses is based on hash of the secret key and the
items’ MSBs hence it is evident that re-sorting attacks
do not alter the watermarking detection results), and
subset selection (up to 50% data cuts). Although, sub-
set addition attack is not discussed by the authors. The
attacker inserts multiple instances of the same item in
the set to distort the subsets used for watermark de-
tection. On an average,
n
2×y
subsets are distorted. The
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
142

watermark detection is affected based on the proper-
ties of elements that jump from one subset to another.
The effectiveness of this attack needs to be measured
experimentally, however, in Section 2.1, we provide
a theoretical estimate of this SWS’s resilience against
subset addition attack.
Input : Bit b, Subset S
i
Output: bit embedded status
return success if ((b = 1 and v
c
(S
i
) > v
true
× y)
or (b = 0 and v
c
(S
i
) < v
false
× y));
if b = 1 then
while true do
Select it
1
,it
2
∈ S
i
≤ avg(S
i
) + c× δ(S
i
);
if it
1
,it
2
found then
while it
1
≤ avg(S
i
) + c× δ(S
i
) do
it
1
= it
1
+incrementValue;
it
2
= it
2
−incrementValue;
return failure if DUC violated;
end
return success if v
c
(S
i
) > v
true
× y;
end
end
else
while true do
Select it
1
,it
2
∈ S
i
> avg(S
i
) + c× δ(S
i
);
if it
1
,it
2
found then
while it
1
> avg(S
i
) + c× δ(S
i
) do
it
1
= it
1
−incrementValue;
it
2
= it
2
+incrementValue;
return failure if DUC violated;
end
return success if v
c
(S
i
) < v
false
× y;
end
end
end
return failure;
Algorithm 1: Single watermark bit insertion.
2.1 Drawbacks of SWS
From our discussion above, we have identified the fol-
lowing drawbacks of SWS:
1. We need to preserve each subset’s average dur-
ing watermark insertion. If the watermark bit is
1, then we choose two items, it
1
,it
2
< avg(S
i
) +
c× δ(S
i
) and increase it
1
while decreasing it
2
un-
til it
1
≥ avg(S
i
) + c × δ(S
i
). The condition in-
creases the standard deviation and the value of
avg(S
i
) + c× δ(S
i
) is different during watermark
detection. This value should be remain the same
during insertion and detection. Hence, instead of
using avg(S
i
) + c× δ(S
i
) as a bound, c× avg(S
i
)
should be used.
2. The scheme is applicable to numeric set that
follow a normal distribution; a theoretical bell-
shaped data distribution that is symmetrical
around the mean and has a majority of items con-
centrated around the mean. This is not practical
in real life since a lot of candidate numeric sets
watermarking might not be normally distributed.
Secondly, even if we assume that the set is nor-
mally distributed, the chances of each subset fol-
lowing a normal distribution are even lower. Thus,
a watermarking scheme should be independent of
the data distribution.
3. The sorting mechanism assumes that small
changes to the items do not alter the subset cat-
egorization, which is based on MSBs. How-
ever, small modifications can change an item’s
MSBs when the item lies in the neighborhood
of 2
x
(let the set containing such items be
N ) for x ∈ Z. For example, subtracting two
from 513 (1000000001)
2
would change it to 511
(0111111111)
2
, thereby modifying the MSBs.
The attacker can hence, select these items and add
a small value to the items in the left N so that they
jump to the right neighborhood and vice-versa.
SWS does not address this constraint and possible
solutions.
4. The watermarking scheme actually relies on the
enormity of available bandwidth with majority
voting being used to determine the correct water-
mark bit. For an m-bit watermark that is embed-
ded l times, the data set needs to have m× l × y
items. As an illustrative figure, for a 32-bit wa-
termark to be embedded just five times in subsets
containing 20 items, we need to have 3,200 items
in the set.
5. Vulnerable to addition attacks: Assume that the
adversary adds ¯n instances of the same item to the
original set of n items. The number of items in
the new set is n
′
= n + ¯n. The added items are
adjacent to each other in the sorted set, which
is divided into y subsets, each containing n
′
/y
items. The starting index of the added items can
be 1,...,n + 1 with equal probabilities . Let the
probability of detecting the watermark correctly
be P(A ,i), where the starting index of the added
items is i in the sorted set. Therefore, the overall
detection probability is =
1
n+1
∑
n+1
i=1
P(A ,i). From
Figure 1, the modified subsets are divided into
three categories:
(a) G
1
: Subsets containing items with index lower
than that of added items and not containing any
added items.
(b) G
2
: Subsets containing added items.
ROBUST AND REVERSIBLE NUMERICAL SET WATERMARKING
143

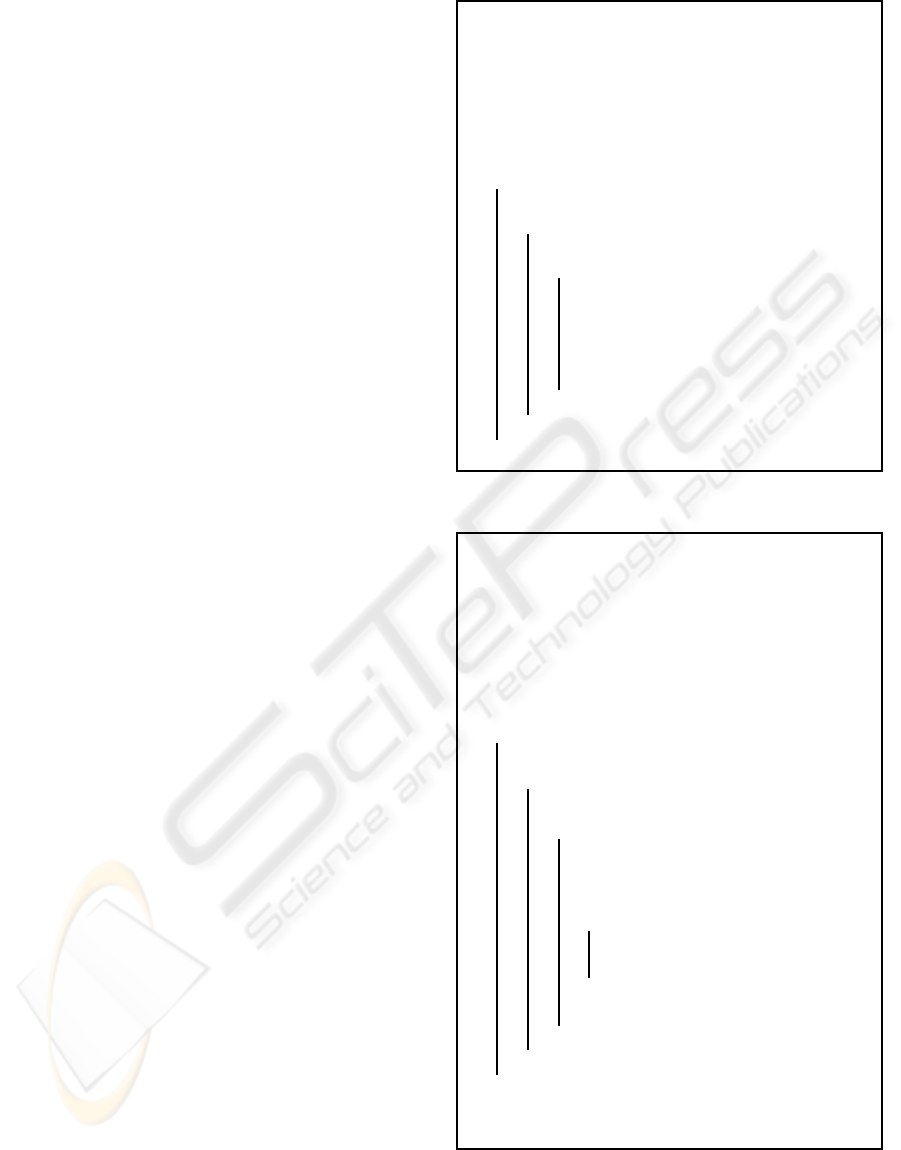
n
Original set
Set after data addition
-
-
-
-
n + ¯n
G
1
G
2
G
3
-
n
y
-
n+¯n
y
-
 -
added by attacker
Figure 1: Subset generation after data addition attack (mul-
tiple instances of the same item added - their location in the
sorted set represented in red line).
(c) G
3
: Subsets containing items with index higher
than that of added items and not containing any
added items.
Each modified subset S
′
i
∈ G
1
contains σ
i
=
n
y
−
i ×
¯n
y
items of original subset S
i
and ζ
i
= i ×
¯n
y
items of the next original subset S
i+1
. At some
point of time, either the added items are encoun-
tered, or, σ
i
becomes 0 (since gcd(n, ¯n) > 1). In
the second condition, modified subset S
′
i
will con-
tain
n
y
− i ×
¯n
y
items of next original subset S
i+1
and ζ
i
items of S
i+2
(σ
i
is 0 in this case, since the
subset does not contain any of the original items).
Thus, the probability of the correct watermark bit
w
i
being detected in subsets in G
1
is F (σ
i
,
n
′
y
)
where F (a,b) is the probability of the correct wa-
termark bit being detected in a subset with a of
the original b items remaining. The probability of
all |G
1
| watermark bits being detected correctly is
given as follows:
P(d
1
) =
|G
1
|
∏
i=1
F (σ
i
,
n
′
y
) (5)
The second group G
2
can be further divided into
two categories:
(a) G
2
1
: Subsets containing both original and new
items from the same subset (the only possibility
of this is with the first subset in G
2
).
(b) G
2
2
: Subsets containing none of the original
items.
Watermark detection probability in G
2
1
is
F (σ
(|G
1
|+1)
1
,
n
′
y
), and in G
2
2
is F (0,
n
′
y
), achiev-
ing an overall watermark detection probability
given below.
P(d
2
) = F (σ
(|G
1
|+1)
1
,
n
′
y
) ×
|G
2
−1|
∏
i=1
F (0,
n
′
y
) (6)
None of the subsets have the original items in G
3
and therefore the probability of detecting the wa-
termark correctly equals:
P(detect
3
) =
|G
3
|
∏
i=1
F (0,
n
′
y
) (7)
The overall probability of detecting the water-
mark in the new set, P(detected), is, P(detect
1
)×
P(detect
2
) × P(detect
3
). F (0,−) is negligible
since the subset contains none of the original
items. It can be see that P(detected) depends on
the starting index of the added items in the mod-
ified set; if the added items are towards the front
of the index-based sorted set, then the watermark
is more likely to be erased.
3 PROPOSED SCHEME
We propose a watermarking scheme that inserts a sin-
gle watermark bit in each of the items selected from
a numeric set. During detection, we check if an item
carries a watermark bit and verify whether the bit ex-
tracted from the watermarked item matches the ex-
pected watermark bit. If the proportion of items for
which the extracted bit matches the watermark bit, to
the total number of item carrying a watermark bit, is
above a certain threshold, the watermark is success-
fully detected.
During the insertion algorithm, the watermark
should ideally be spread evenly across the set and
should be sparse enough so that the watermark can
survive active attacks. We distribute the watermark
evenly across the set by selecting the items based on
their MSBs. It is possible to make it sparse enough by
embedding a watermark bit in one of every γ items.
This can be done by checking if γ divides λ, where λ
is a one way hash on a concatenation of MSB( f,s
i
)
and a secret key K , shown as follows:
λ = H (MSB( f,s
i
)kK ) (8)
We assume that we have ξ LSBs that can be mod-
ified without substantially reducing the data’s utility
(value of ξ can be adjusted by the owner). The maxi-
mum distortion to the data without compromising it’s
quality is 2
ξ
.
The watermark bit is λ (mod 2). The owner
marks v out of n items. If the detection algorithm
identifies v
′
items to be watermarked, out of u
′
items
carry the correct bit, then watermark presence is es-
tablished if
u
′
v
′
> α. Higher values of confidence level
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
144

α imply lower false positive probability but lower re-
silience against attacks. The value α should be set to
an optimal value, usually between 0.6 and 0.8.
Finally, the bit location to be replaced by the wa-
termark bit is identified. We input the maximum per-
centage change that can be introduced in an item, ε,
and generate ξ = ⌈log
2
(s
i
× ε)⌉. We insert the re-
placed bit into the fractional part to enable reversibil-
ity. We can choose the location at which this bit is
inserted in the fraction part as τ = λ (mod β), where
β is the number of bits used to store the fraction part.
As discussed in Section 2.1, even a small distor-
tion during insertion or by the attacker can result in
modifying MSBs if the item lies in N and therefore
affect the detection process.
Let there be one of out of ε items from S in N .
Upon inserting a bit in an item from N , the water-
marked item is ignored during detection with a prob-
ability of (γ − 1)/γ, which simply reduces the num-
ber of items in which the watermark bits are de-
tected. There is a 1/γ probability that the modified
item is still detected as carrying a watermark bit (Al-
gorithm 19, line 5). When this happens, there is a 50%
probability that the bit detected is, in fact, the correct
watermark bit (Algorithm 19, line 11). Thus the over-
all probability that the watermark bit being detected
incorrectly is 1/(2εγ). In normal circumstances, this
is less than 1% since usually ε < 10 and γ ≈ 10.
In stricter conditions where even a small propor-
tion of watermark bits getting affected is unaccept-
able, a solution is to ensure that abs(s
i
− 2
x
) > 2
ξ
,
where abs(x) is a function that returns the abso-
lute value of a number x ∈ R. Thus, an item s
i
is
chosen for carrying a watermark bit if λ (mod γ) =
0 AND abs(s
i
− 2
x
) > 2
ξ
. From a security perspec-
tive, the attacker can ignore n/ε items that are in N
while trying to remove the watermark, but apart from
that, (s)he does not get any benefit.
3.1 Watermarking Algorithms
The insertion and detection processes are pro-
vided in Algorithms Please place \label after
\caption, 19 respectively. In these algorithms
lsb(x, y) refers to y
th
LSB of value x.
Input : Numeric set S = {s
1
,... ,s
n
}, change
limit ε, bits used for fraction part β,
Secret key K , Watermarking fraction
γ
Output: Watermarked set S
w
λ = H (MSB( f,s
i
)kK );
τ = λ (mod β);
for i = 1 to n in steps of 1 do
ξ = ⌈log
2
(s
i
× ε)⌉;
if λ (mod γ) = 0 then
//2
x
is the power of 2 closest to s
i
;
if abs(s
i
− 2
x
) > 2
ξ
then
int = ⌊s
i
⌋;
frac = s
i
− int;
b = λ (mod ξ);
lsb( frac,τ) = lsb(int,b);
lsb(int,b) = λ (mod 2);
end
end
end
Algorithm 2: Watermark insertion.
Input : Watermarked set S
w
, change limit ε,
bits used for fraction part β, Secret
key K , Watermarking fraction γ,
confidence level α
Output: Watermark presence status, Original
set S = {s
1
,... ,s
n
}
λ = H (MSB( f,s
i
)kK );1
τ = λ (mod β);2
for i = 1 to n in steps of 1 do3
ξ = ⌈log
2
(s
i
× ε)⌉;4
if λ (mod γ) = 0 then5
//2
x
is the power of 2 closest to s
i
;6
if abs(s
i
− 2
x
) > 2
ξ
then7
int = ⌊s
i
⌋;8
frac = s
i
− int;9
b = λ (mod ξ);10
if lsb(int,b) = λ (mod 2) then11
match = match+ 1;12
lsb(int,b) = lsb( frac, τ);13
end14
total = total+ 1;15
end16
end17
end18
return true if lsb(int, b) = λ (mod 2),19
otherwise false;
Algorithm 3: Watermark detection.
ROBUST AND REVERSIBLE NUMERICAL SET WATERMARKING
145

4 ANALYSIS AND
EXPERIMENTAL RESULTS
4.1 False Positive Probability
First we discuss the false positive probability of our
watermarking scheme. That is, what are the chances
of a watermark detection algorithm detecting a wa-
termark in an unmarked set S with parameters secret
key K , fraction γ and confidence level α. The num-
ber of items in a random set identified as containing
watermark bit are n
′
=
n
γ
and probability that the wa-
termark bit will be detected correctly for an item is
1/2. Hence, at least α proportion of watermark bits
identified correctly is given in Equation 9. This false
positive probability is extremely and has shown to be
around 10
−10
in (Agrawal and Kiernan, 2002).
n/γ
∑
i=α×n/γ

n/γ
i

(1/2)
i
× (1/2)
n/γ−i
=
n/γ
∑
i=α×n/γ

n/γ
i

(1/2)
n/γ
= 2
−n/γ
×
n/γ
∑
i=α×n/γ

n/γ
i

(9)
4.2 Security
The attacks and our scheme’s resilience to them is
provided next:
1) Set Re-ordering. The re-ordering attack is ineffec-
tive against the watermarking model since each item
is individually watermarked and checked for water-
mark bit presence.
2) Subset Addition. Let the attacker add subset S
1
containing n
add
items to the watermarked set S
2
con-
taining n items.
n
γ
out of
n
γ
watermark bits will still
be detected correctly in S
2
. From S
1
, a total of
n
add
γ
will probabilistically be detected as marked and for
each item considered to be marked, watermark bit will
be detected correctly with a a 0.5 probability. Thus,
the expected number of correctly detected bits from
S
2
is
n
add
2×γ
. The overall watermark detection ratio is
1+n
add
/(2n)
1+n
add
/n
. For 50% (
n
add
n
=
1
2
), and 100% (
n
add
n
= 1)
data additions, the expected watermark detection ratio
is
5
6
and
3
4
respectively. For α = 0.7. The adversary
needs to add at least 150 items for every 100 items in
the watermarked set to have a decent chance of de-
stroying the watermark. For α = 0.6, the number of
items that need to be added to destroy the watermark
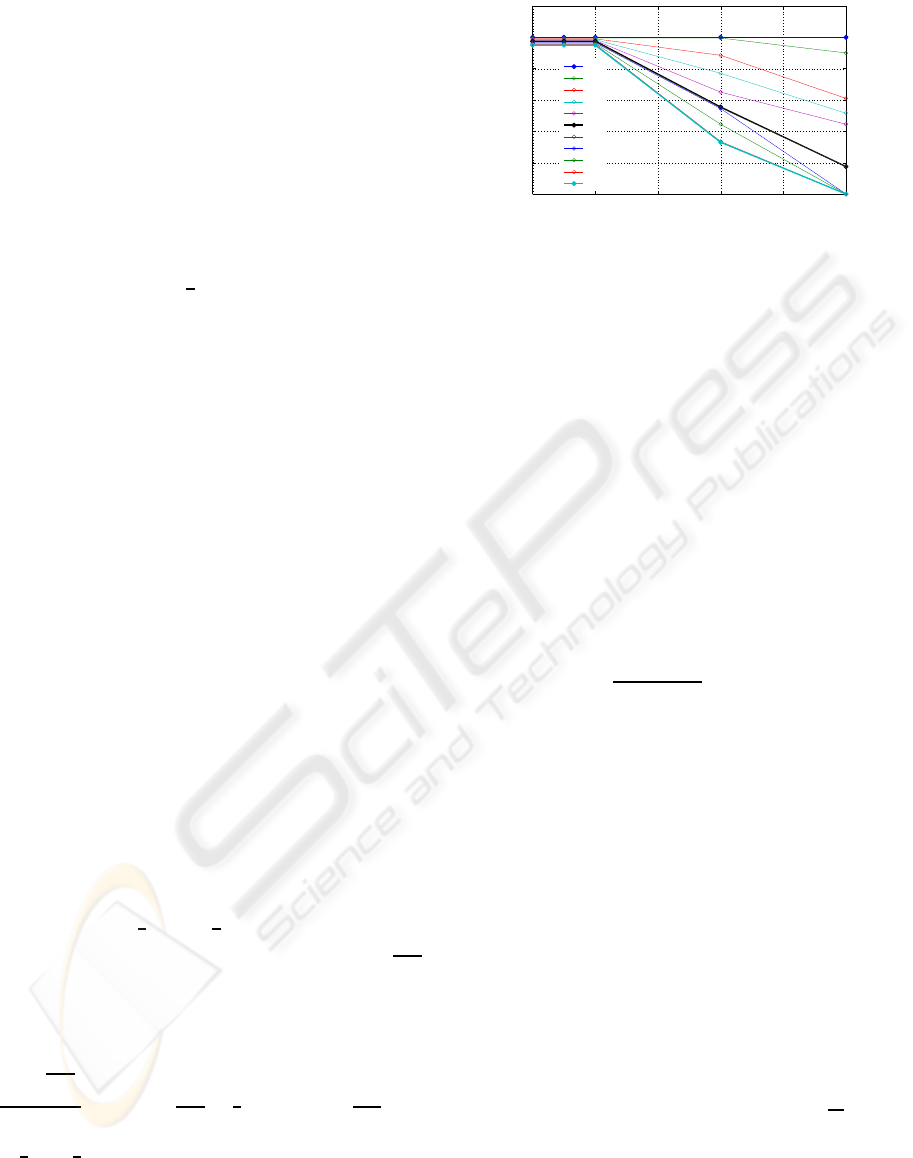
50 100 150 200 250 300
0
0.2
0.4
0.6
0.8
1
1.2
$n
add
× 100$
Watermark survival ratio
0.60
0.61
0.62
0.63
0.64
0.65
0.66
0.67
0.68
0.69
0.7
α
Figure 2: Watermark survival with varying α, n
add
.
increases to 400 items for every 100 items. Such lev-
els of data addition are bound to have derogatory ef-
fect on data usability. Figure 1 illustrates the variation
of watermark detection ratio with increasing levels of
data addition.
Experimental results from data addition attacks
are given in Figure 2. The findings confirm our claim
with all watermarked sets surviving attacks of up to
300% data addition for α = 0.6, and 95% of the wa-
termarked sets surviving attacks of up to 100% data
addition for α = 0.7.
3) Subset Deletion. We assume that the attacker
deletes n
remove
items from the watermarked set con-
taining n items, leaving n − n
remove
items. The re-
moved items have equal probability of being water-
marked as the remaining items. Thus, the watermark
detection ratio is
(n−n
remove
)/γ
(n−n
remove
)/γ
= 1. But this does not
mean that the watermarking scheme is uncondition-
ally secure against subtractive attacks. If the number
of remaining elements is extremely low, the false pos-
itive probability becomes unacceptably high and the
adversary can claim that the watermark detection was
accidental. However, it is only in the interest of the
adversary to leave sufficient items so that the set is
still useful.
4 a) LSB Distortion. We assume that the attacker
has the knowledge of ξ for this discussion.This is to
provide additional strength to the attack and thereby
provide the worst case security analysis of the water-
marking model. The attacker chooses n
d
items out
of the total n items and flips all ξ bits in an attempt
to erase the watermark. The watermark detection
will detect the watermark bits incorrectly from the n
d
items and, correctly from the other n− n
d
items. The
watermark detection ratio in this case is 1 −
n
d
n
. This
ratio needs to be at least α to detect the watermark.
Hence, the upper limit on items that can be deleted
from the subset is n
d
≤ n × (1 − α). For α = 0.7, a
maximum of 30% items can be removed such that the
watermark is preserved.
Experimental results of LSB distortion attack are
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
146

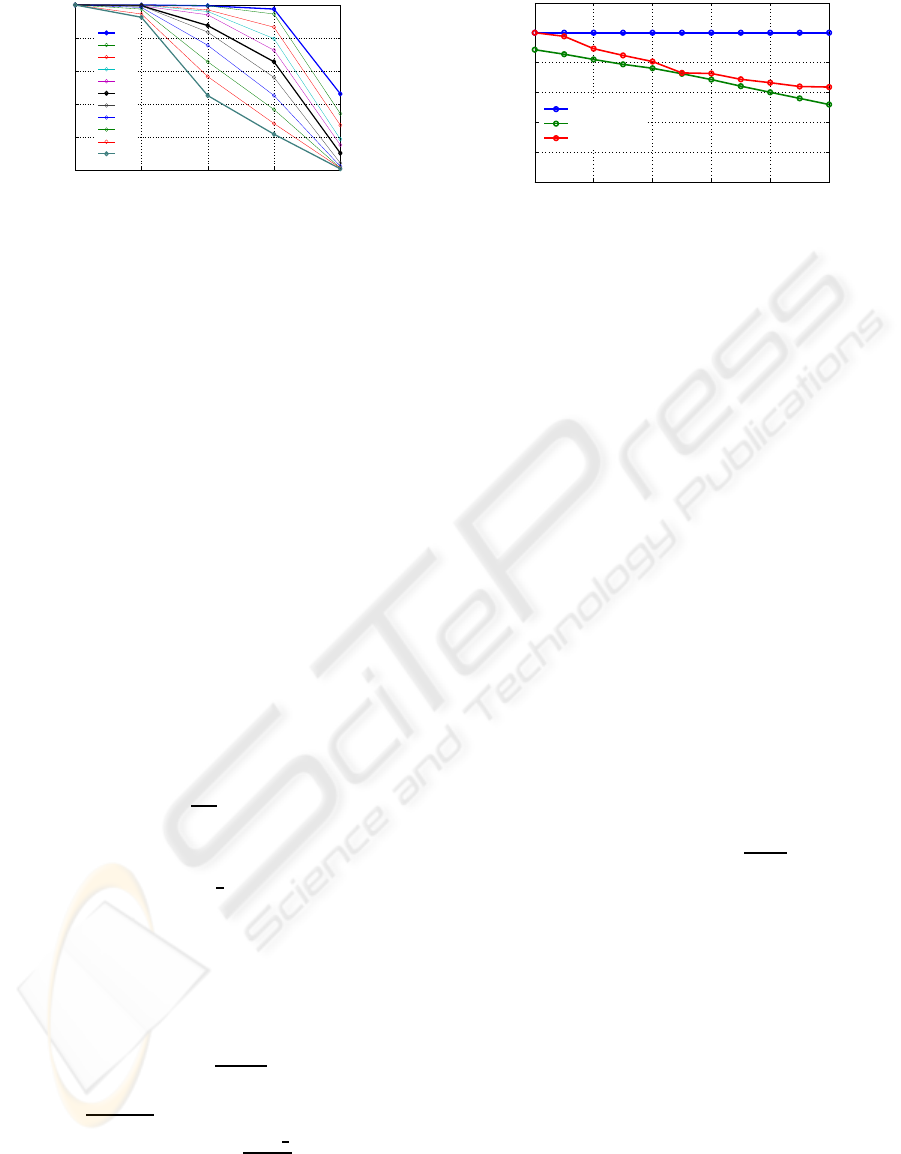
20 25 30 35 40
0
0.2
0.4
0.6
0.8
1
$n
d
× 100$
Watermark survival ratio
0.60
0.61
0.62
0.63
0.64
0.65
0.66
0.67
0.68
0.69
0.7
α
Figure 3: Watermark with varying α,n
d
.
provided in Figure 3. The experiment was run on 200
numerical sets and computed the proportion of the
times watermark survived when all ξ LSBs of 20%
to 40% data items were flipped. The results show that
the watermarking scheme is extremely secure against
LSB bit flipping attacks for LSBs of 25% items being
flipped. For 35% attack, the watermark survived an
average of 62% times. For α = 0.60, the watermark
survival rate drops to 46% times when attack level in-
creases to 40%. We infer from experimental results
that the optimal value of α is around 0.65, with which
watermark has a high survival possibility and at the
same time has a low false positive probability.
4 b) MSB Distortion. We assume that the attacker
has the knowledgeof f for this discussion. Again, this
makes the adversary stronger and provides us with an
estimate of the watermark’s resilience against acute
attacks. The attacker chooses n
d
items out of the total
n items and flips all f MSBs, resulting in modified
λ. The watermark detection will detect the watermark
bits correctly from the other n − n
d
items. For the
items with distorted MSBs, there are two cases:
1. With a probability of
γ−1
γ
, λ (mod γ) 6= 0 and the
item is not considered as carrying a watermark bit.
2. With a probability of
1
γ
, λ (mod γ) = 0 and
the item is still considered as carrying a water-
mark bit. There is a probability of 1/2 that (λ
(mod ξ))
th
LSB equals λ (mod 2).
The following is an analysis of the expected value
of watermark detection ratio. Within the distorted
subset, the expected number of items considered as
carrying a watermark bit is
n
d
−γ+1
γ
and the expected
number of items in which watermark bit is detected
correctly is
n
d
−γ+1/2
γ
. Expected value of watermark
detection ratio in the final set is
n−γ+
1
2
n−γ+1
.
We can see that, on an average, for sufficiently
large n− γ, the expected watermark detection ratio af-
ter MSB modification attack is very close 1. During
our experiments, the watermarks were detected at all
0.6 0.62 0.64 0.66 0.68 0.7
0
0.2
0.4
0.6
0.8
1
α
Watermark survival ratio
MSB distortion
LSB distortion
Data addition
Figure 4: Watermark survival with varying α.
times with all f MSBs of 20% to 40% items being
flipped.
The average watermark survival proportion under
the three significant attacks of LSB distortion, MSB
distortion, and data addition are presented in Figure 4.
It can be seen from the figure that α = 0.65 is the opti-
mal value, where the watermark has a high chance of
survival while having a low false positive probability.
5) Secondary Watermarking. The security of the
watermarking scheme against secondary watermark-
ing attacks comes from the reversibility operation
(storing the original bit replaced by the watermark bit
in the fraction part). If r parties, O
1
,... ,O
r
watermark
the same numeric set sequentially, then the objective
is for the first party O
1
to be established as origi-
nal and rightful owner. It has been shown in (Gupta
and Pieprzyk, ) that owner identification is facilitated
by watermarking schemes that provide reversibility.
Based on the experimental results, the current water-
marking scheme provides security against secondary
watermarking attacks with r ≤ 5.
The watermark carrying capacity of the water-
marking scheme is |{s
i
: (abs(s
i
− 2
x
) > 2
ξ
)}|/γ,
where 2
x
is the power to 2 closest to s
i
. This is
much higher than the capacity of
|S|
|S
i
|×m
offered by
SWS, where |S| is the size of the numeric set, |S
i
|
is the size of the subsets and m is the number of
times each watermark bit must be inserted. We de-
signed experiments to test the watermarking capaci-
ties of both schemes with the sets ranging from 1000
to 3000 items, each watermark bit being embedded
1 to 5 times in subsets containing 25 to 200 items
for SWS. Our scheme had an average watermarking
capacity of 8.28% for the 60 experiments while the
overall average of SWS was 0.86%. The summary of
results is presented in Figure 5.
ROBUST AND REVERSIBLE NUMERICAL SET WATERMARKING
147

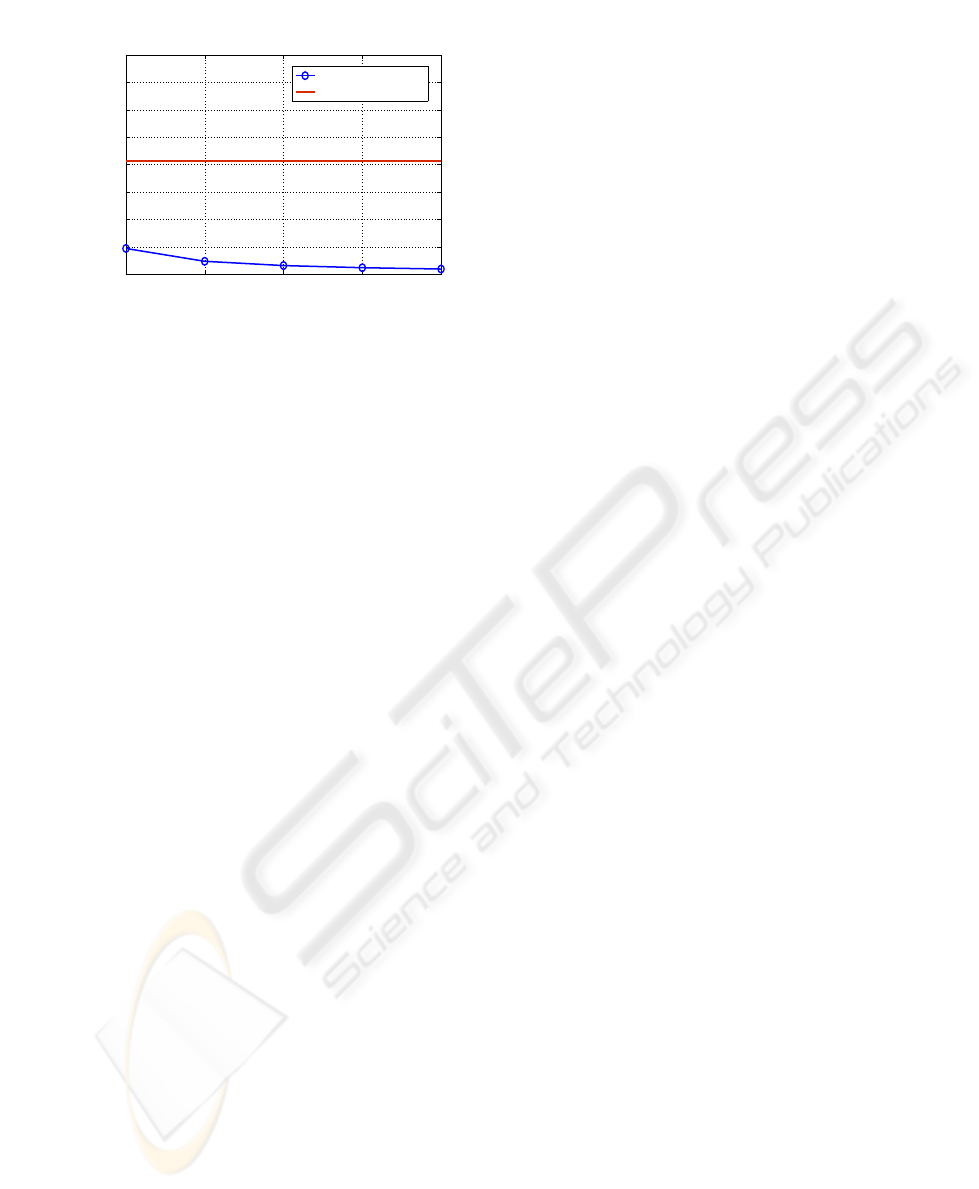
1 2 3 4 5
0
2
4
6
8
10
12
14
16
Number of times each watermark bit is embedded for SWS
Watermarking capacity in percentage
SWS capacity
Our scheme’s capacity
Figure 5: Comparison of our scheme’s watermarking ca-
pacity with SWS.
5 CONCLUSIONS AND FUTURE
WORK
We have proposed a watermarking model for numeric
sets in this paper. The watermarking scheme embeds
one watermark bit for every γ items in the numeric
set of size n, thereby offering a watermark carrying
capacity close to n/γ. The major improvement of-
fered by our scheme is in terms of the lack of con-
straints on the characteristics of the numeric set to be
watermarked. Unlike (Sion et al., 2002), where the
numeric set to be watermarked should follow normal
distribution, the watermarking scheme is applicable
to a numeric set irrespective of it’s distribution and it
is shown that the watermark survives against data ad-
dition, deletion, distortion, re-sorting attacks as well
as secondary watermarking attacks. The capacity of
the watermarking scheme is also higher than that of
the previous scheme.
The current scheme embeds a detectable water-
mark in the numeric set and not an extractable wa-
termark. Our future work is directed towards finding
ways to embed an extractable watermark in the nu-
meric set whilst providing the same level of security
and capacity offered by our current scheme.
REFERENCES
Agrawal, R. and Kiernan, J. (2002). Watermarking rela-
tional databases. In Proceedings of the 28th Interna-
tional Conference on Very Large Databases VLDB.
Atallah, M., Raskin, V., Crogan, M., Hempelmann, C., Ker-
schbaum, F., Mohamed, D., and Naik, S. (2001). Nat-
ural language watermarking: design, analysis, and a
proof-of-concept implementation. In Proceedings of
4th Information Hiding Workshop, LNCS, pages 185–
199, Pittsburgh, Pennsylvania. Springer-Verlag, Hei-
delberg.
Bolshakov, I. A. (2005). A method of linguistic steganogra-
phy based on collocationally-verified synonymy. In In
Proceedings of 4th International Workshop on Infor-
mation Hiding, IH 2004, volume 3200 of LNCS, pages
180–191. Springer Verlag.
Bors, A. and Pitas, I. (1996). Image watermarking using
dct domain constraints. In Proceedings of IEEE Inter-
national Conference on Image Processing (ICIP’96),
volume III, pages 231–234.
Collberg, C. and Thomborson, C. (1999). Software wa-
termarking: Models and dynamic embeddings. In
Proceedings of Principles of Programming Languages
1999, POPL’99, pages 311–324.
Cox, I. J., Killian, J., Leighton, T., and Shamoon, T. (1996).
Secure spread spectrum watermarking for images, au-
dio, and video. In IEEE International Conference on
Image Processing (ICIP’96), volume III, pages 243–
246.
Gupta, G. and Pieprzyk, J. Reversible and blind database
watermarking using difference expansion. Inter-
national Journal of Digital Crime and Forensics,
1(2):42.
Qu, G. and Potkonjak, M. (1998). Analysis of watermarking
techniques for graph coloring problem. In Proceed-
ings of International Conference on Computer Aided
Design, pages 190–193.
Sebe, F., Domingo-Ferrer, J., and Solanas, A. (2005).
Noise-robust watermarking for numerical datasets.
Lecture Notes in Computer Science, 3558:134–143.
Sion, R., Atallah, M., and Prabhakar, S. (2002). On water-
marking numeric sets. In Proceedings of First Inter-
national Workshop on Digital Watermarking, IWDW
2002. LNCS, volume 2163, pages 130–146, Seoul,
Korea. Springer-Verlag, Heidelberg.
Sion, R., Atallah, M., and Prabhakar, S. (2004). Rights
protection for relational data. IEEE Transactions
on Knowledge and Data Engineering, 16(12):1509–
1525.
Venkatesan, R., Vazirani, V., and Sinha, S. (2001). A graph
theoretic approach to software watermarking. In Pro-
ceedings of 4th Information Hiding Workshop, LNCS,
volume 2137, pages 157–168.
Zhang, Y., Niu, X.-M., and Zhao, D. (2004). A method
of protecting relational databases copyright with cloud
watermark. Transactions of Engineering, Computing
and Technology, 3:170–174.
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
148