
A HIGH-LEVEL KERNEL TRANSFORMATION RULE SET FOR
EFFICIENT CACHING ON GRAPHICS HARDWARE
Increasing Streaming Execution Performance with Minimal Design Effort
Sammy Rogmans
1,2
, Philippe Bekaert
1
and Gauthier Lafruit
2
1
Hasselt University – tUL – IBBT, Expertise centre for Digital Media, Wetenschapspark 2, 3590 Diepenbeek, Belgium
2
Multimedia Group, IMEC, Kapeldreef 75, 3001 Leuven, Belgium
Keywords:
High-level, Transformation, Rule set, GPU, Efficient.
Abstract:
This paper proposes a high-level rule set that allows algorithmic designers to optimize their implementation
on graphics hardware, with minimal design effort. The rules suggest possible kernel splits and merges to
transform the kernels of the original design, resulting in an inter-kernel rather then low-level intra-kernel
optimization. The rules consider both traditional texture caches and next-gen shared memory – which are used
in the abstract stream-centric paradigms such as CUDA and Brook+ – and can therefore be implicitly applied
in most generic streaming applications on graphics hardware.
1 INTRODUCTION
The landscape of parallel computing has been signifi-
cantly altering during these latest few years. Since the
beginning of the programmability of Graphics Pro-
cessing Units (GPUs), it was very clear for the high-
performance computing community that GPUs could
be exploited as powerful coprocessors. General-
purpose GPU (GPGPU) computing has therefore pro-
liferated the use of data parallel programming, cer-
tainly since the introduction of abstract programming
environments such as CUDA and Brook+. These
paradigms abstract the GPU as a hybrid distributed-
shared memory architecture, having multiple multi-
processors, each with their individual shared memory.
The popularization of data parallel programming
has triggered researchers to investigate and formal-
ize mapping rules to fit sequentially modelled algo-
rithms on the parallel GPU architecture. Owens et al.
has been systematically surveying traditional GPGPU
(Owens et al., 2007), where the computational re-
sources can only be exploited through the graphics
APIs Direct3D or OpenGL. More recently, the next-
generation GPGPU vendor-specific APIs CUDA and
Brook+ were released for NVIDIA and ATI hard-
ware respectively. Abstracting the graphics hardware
through these generic APIs has further levered the
motivation to investigate formal mapping rules to the
GPU architecture. As the GPU exhibits a massive
parallel architecture, the main challenge for the map-
ping rules is to keep the processors busy instead of
idle due to relatively slow memory reads. The pre-
liminary visions and statements of the university of
California at Berkeley in (Asanovic et al., 2006) state
that there are an important set of elementary ker-
nels – consistently defined as dwarfs – which has led
many researchers to investigate intra-kernel optimiza-
tion and formalization. Govindaraju et al. created
a memory model for traditional GPGPU in (Govin-
daraju et al., 2006), where the memory efficiency
of a kernel can be modelled and examined. How-
ever, research such as (Fatahalian et al., 2004) proves
that some stand-alone kernels cannot be optimized
and are therefore always bound by a memory bot-
tleneck, most certainly with the constraints of tradi-
tional GPGPU. Ryoo et al. investigated many possi-
ble intra-kernel optimizations in (Ryoo et al., 2008)
when considering next-generation GPGPU. Nonethe-
less, Victor Podlozhnyuk shows in his image convolu-
tion tutorial for CUDA (Podlozhnyuk, 2007) that tra-
ditional (texture) memory access can be more bene-
ficial in some cases. Therefore, traditional and next-
gen GPGPU are in general not mutually exclusive in
an end-to-end optimized application.
Complementary to previous related research on
low-level intra-kernel optimization, this paper rather
38
Rogmans S., Bekaert P. and Lafruit G. (2009).
A HIGH-LEVEL KERNEL TRANSFORMATION RULE SET FOR EFFICIENT CACHING ON GRAPHICS HARDWARE - Increasing Streaming Execution
Performance with Minimal Design Effort.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 38-43
DOI: 10.5220/0002188400380043
Copyright
c
SciTePress

Figure 1: Concepts of a streaming kernel.
focusses on a high-level rule set with regards to form a
methodology for inter-kernel optimization. The most
important concepts related to an individual kernel are
(see Fig. 1) the input stream(s), the computations in-
side, and the output stream(s). Moreover, two im-
portant performance specifications of a kernel are the
arithmetic intensity and processor occupancy. Arith-
metic intesity defines the ratio of the amount of com-
putations inside the kernel, to the total amount of data
transfered. In contrast with arithmetic intensity that
is already used for years, processor occupancy is rel-
atively new, and specifies the amount of data parallel
thread batches (i.e. CUDA warps) that are able to si-
multaneously execute per individual (multi)processor.
In Section 2 we describe the formal rule set that opti-
mizes a stream-centric processing chain, while moti-
vating the rules in an abstract processing level. Sec-
tion 3 consequently presents a case study and its re-
sults, optimizing the truncated windows (Lu et al.,
2007; Rogmans et al., 2009) algorithm, which com-
putes a dense depth map out of a rectified stereo im-
age input. The conclusion and possible future work is
ultimately presented in Section 4.
2 HIGH-LEVEL RULE SET
By splitting and merging kernels in the high-level
design, the specifications of the resulting individual
kernels can be altered for optimal end-to-end perfor-
mance. Nonetheless, proper care should be taken, as
a random kernel split or merge could influence the
performance negatively. The proposed rule set de-
fines the plausible kernel splits and merges to bene-
fit the overall performance, and can therefore assist a
GPGPU programmer to optimize an implementation
with minimal design effort. The motivation of split-
ting should always be to lever the processors occu-
pancy of the kernel. If a kernel is split, the memory
footprint – i.e. the temporary memory and registers
needed for the kernel computations – is consequently
reduced. As a single thread consumes less mem-
ory, the amount of threads that can be managed si-
multaneously on a single (multi)processor with fixed
amount of shared memory and registers, is thereby
significantly increased. Although this levers the pro-
cessor occupancy, a kernel split could potentially hurt
the arithmetic intensity when the two resulting sub-
kernels exhibit redundant input and/or output streams.
Merging two kernels should always be motivated
by levering the arithmetic intensity. Since two ker-
nels communicate through global memory, this com-
munication can be completely avoided. Nevertheless,
a random merge could potentially increase the mem-
ory footprint of a kernel, and therefore damage its
processor occupancy. Moreover, in some cases the
arithmetic intensity can suddenly proliferate due to
implicit data dependencies between the two merged
kernels, resulting in a non-trivial computational bot-
tleneck. As kernel merging and splitting can hence
crosswise counter the kernel specifications while at-
tempting to improve the performance, the rule set pro-
poses only those rules which will improve either arith-
metic intesity or processor occupancy, without nega-
tively affecting the other spec.
2.1 Kernel Splits
Splitting kernels to lever the occupancy while main-
taining the arithmetic intensity, can be applied in two
different forms, depending on the input streams of the
kernel that potentially needs to be split. Whenever
a single input stream can be isolated to a sub-kernel
functionality, the sub-kernel functionality can be seen
to be only dependent of a single preceding kernel, and
can therefore be extracted without breaking any data
dependencies.
In contrast, a kernel that has input streams com-
ing from multiple preceding kernels, cannot be easily
split without breaking data dependencies. However,
the kernel can be duplicated by restructuring the data
streams, while still having a beneficial effect in over-
all performance.
2.1.1 Rule (1): Input Isolation
“If a data input stream can be isolated to a spe-
cific sub-kernel functionality, the concerning kernel
should be split into two kernels harnessing the iso-
lated sub-kernel functionality and the remaining part.
The jointly generated kernel should be recursively
checked for the further application of this rule.”
As depicted in Fig. 2a, a sub-kernel functionality
with a random amount of output streams, that is de-
pendent of only a single data input stream, is isolated
to form two different kernels. Both kernels will there-
fore increase their individual processor occupancy,
as their memory footprint is reduced. Moreover,
the footprint of the isolated sub-kernel is minimized,
when assuming the further application of intra-kernel
optimizations. When using traditional texture caches,
A HIGH-LEVEL KERNEL TRANSFORMATION RULE SET FOR EFFICIENT CACHING ON GRAPHICS
HARDWARE - Increasing Streaming Execution Performance with Minimal Design Effort
39
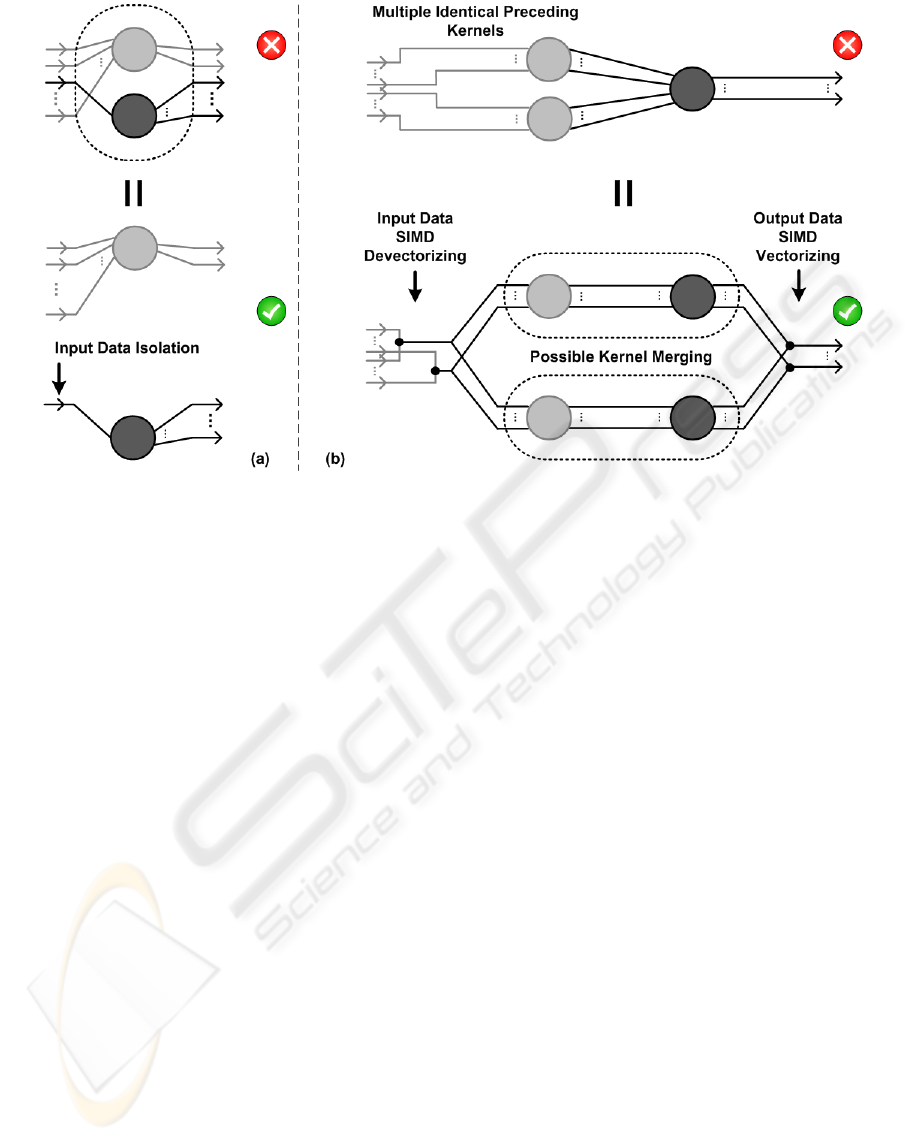
Figure 2: An (a) input isolation and (b) kernel duplication.
this rule will also significantly impact the sampling
rate, and therefore the memory transfer. Sampling
from only a single ‘texture’ or data stream, will al-
low an optimal use of the caches with minimal misses,
most definitely when a linear sampling pattern can be
used. Since the input and output streams can be un-
tangled, no redundancy is necessary, and the average
arithmetic intesity of both kernels is still equivalent to
the original one.
2.1.2 Rule (2): Kernel Duplication
“Kernels that cannot be further split by rule (1), and
have multiple input streams coming from different ker-
nels with the same functionality, can be duplicated by
devectorizing the data streams inside the SIMD com-
ponents of the multiprocessor. The original output
is consequently acquired by revectorizing the output
streams of the duplicated kernels.”
Fig. 2b depicts a duplicated kernel with reduced
number of input streams. The SIMD components
in the streams (i.e. the traditional RGBA-channels,
or next-gen CUDA execution warps) therefore have
to be restructurized. Since the data components of
SIMD are per definition independant, they can be im-
plicitely untangled without breaking any data depen-
dencies. If the preceding kernels exhibit the same
functionality, the individual SIMD components can
be freely interchanged. By doing so, all required (de-
vectorized) scalar input dependencies of the concern-
ing kernel, are transmitted over the outputs of a single
preceding kernel. Hence, the devectorized kernel can
be duplicated to consequently process the output of
each of the identical preceding kernels. For this to
work however, the concerning kernel can no longer
work on its original SIMD size, but offers no con-
crete problems as next-gen GPGPU can function on a
scalar level. The advantage is again that processor oc-
cupancy is levered, while maintaining the arithmetic
intensity, and additionally will allow for a consecu-
tive kernel merge that further levers the overall per-
formance.
2.2 Kernel Merges
Merging kernels can significantly lever the arith-
metic intensity, whenever input streams can be reused
and/or global communication is avoided. In case
input streams can be reused, the individual kernel
computations are packed together into a single ker-
nel. Nevertheless, packing more computations inside
a single kernel can potentially increase the memory
footprint, and therefore reduce the average processor
occupancy.
Whenever the input streams of a kernel are di-
rectly linked to the output streams of a preceding ker-
nel, the stream flow can be simplified – and therefore
avoid global communication – by merging both ker-
nels. The risc of simplifying the flow however, is that
the data dependencies between the two concerning
kernels can proliferate the arithmetic intensity, caus-
ing a computational bottleneck that is larger than the
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
40

Figure 3: A (a) computational packing and (b,c) flow simplification.
original global memory bottleneck.
2.2.1 Rule (3): Computation Packing
“If two different kernels read from identical input
streams and are not inter-dependent, the computa-
tions can be packed into a single kernel with expanded
functionality. The number of input streams therefore
remains equivalent, while the number of outputs is the
sum of the separate output streams.”
As depicted in Fig. 3a, the computations of two
kernels with identical input streams are packed to-
gether. The arithmetic intensity is significantly lev-
ered whenever the two merged kernels share a number
of common input streams, however there is in general
no guarantee that the occupancy does not drop, be-
cause of a possible increase in the memory footprint
of the merged kernel. Nonetheless, when their func-
tionalities are not inter-dependent (i.e. one of the ker-
nels needs the other one’s output as input), the mem-
ory footprint cannot exceed the maximum of both
both individual footprints. This is thanks to the pos-
sibility of clearing the required temporary memory
– excluding the input data – for the following sub-
kernel.
2.2.2 Rule (4): Flow Simplification
“A flow of two kernels that are interconnected sequen-
tially by their respective output and input streams,
can be simplified and merged to a single kernel. The
merge is only implicit optimal whenever the global
memory footprint between the two kernels exhibits a
strict one-to-one relationship. This does not impose
any restrictions on additional outputs or inputs that
do not interconnect the concerning kernels.”
Fig. 3b shows two sequential kernels that are
merged, whereas intermediate in- and output streams
are also allowed in this rule (see Fig. 3c). Since inter-
kernel communication can only occur through global
memory, merging two sequential kernels could avoid
a significant amount of global memory communica-
tion. Whenever the data dependencies between the
two kernels exhibits a one-to-one relationship (e.g. an
RGB to YUV conversion), the result of the first kernel
can be immediately reused without the need of writ-
ing and reading the data to global memory. However,
in the case the two kernels do not exhibit a one-to-
one relationship (e.g. an N-tap convolution filter), the
intermediate results of threads in the vicinity (i.e. the
size of the filter) of the thread block borders cannot be
reused, because thread blocks are not able to commu-
nicate with each other. In this effect, the computations
of the first kernel have to be performed in a redundant
manner, to provide the required input data of the con-
secutive kernel. Whether or not the kernel merge is a
good design choice, is then dependent of the low-level
computations and optimizations, making it difficult to
exactly predict an overall performance increase.
3 CASE STUDY RESULTS
As a case study for the application of the high-level
kernel transformation rules, we present the optimiza-
tion of the truncated windows (Lu et al., 2007) stereo
depth estimation algorithm, with minimal design ef-
fort. Stereo matching has been already intensively re-
searched by the computer vision community, and is
systematically surveyed by (Scharstein and Szeliski,
2002). However, only the latest years these algo-
rithms started to become real-time through the use
of GPGPU computing. Gong et al. and Rogmans et
al. have studied the performance of various important
real-time stereo algorithms in (Gong et al., 2007) and
(Rogmans et al., 2009) respectively. From this pre-
vious research, the truncated windows algorithm is
A HIGH-LEVEL KERNEL TRANSFORMATION RULE SET FOR EFFICIENT CACHING ON GRAPHICS
HARDWARE - Increasing Streaming Execution Performance with Minimal Design Effort
41

Figure 4: The (a) original algorithmic flow sketch and (b,c,d,e) optimization phases.
identified as having one of the best trade-offs between
quality and execution speed, hence we present the fur-
ther optimization of this algorithm.
Following the taxonomy of (Scharstein and
Szeliski, 2002), the truncated windows algorithm ex-
ists out of three phases, i.e. the absolute difference
(AD), a truncated convolution (TC), and a winner-
takes-all (WTA) disparity (depth) selection. As
shown in Fig. 4a, the AD-kernel takes in a left and
right stereo image, and outputs a pixelwise difference
to the TC-kernel that will convolve the input with a
truncated filter, resulting in four separate outputs. The
final WTA-kernel selects the minimal value, as it indi-
cates the best disparity (depth) hypothesis. For more
detail about the algorithm, the reader can consult Lu
et al.’s original paper (Lu et al., 2007).
As Fig. 4a only depicts the basic algorithmic flow
sketch in the first phase, a trivial algorithmic opti-
mization is to separate the 2D convolution in a 1D
horizontal and vertical filter, resulting in the flow dia-
gram shown in Fig. 4b. Since this decreases the algo-
rithmic complexity, it is a perfect example of signifi-
cantly reducing the amount of computations to com-
pensate the extra inter-kernel communication. How-
ever, many algorithmic designers do not go beyond
these optimizations, as most of the time further opti-
mizations require platform-specific knowledge.
The specific GPU architectural knowledge is con-
veniently embedded inside the proposed high-level
rules, to destress the designer from first going through
a rather though learning curve. In a third phase, the
first rule can be applied on the vertical convolution,
since the horizontal convolution kernel outputs a left
(L) and right (R) part. Instead of reading from both
streams, the streams are now read separately and pro-
cessed individually to an upper (U) and lower (D)
SIGMAP 2009 - International Conference on Signal Processing and Multimedia Applications
42

part, shown in Fig. 4c. As previously discussed, this
significantly improves the use of traditional texture
caches, and levers the processor occupancy in case of
next-gen shared memory. The arithmetic intensity is
left clearly untouched with this transformation.
The WTA-kernel now inputs from both vertical
convolution filters (see Fig. 4d). Since they both per-
form the same functionality, but on different data, the
WTA-kernel can be duplicated according to rule (2).
The be able to apply this rule, the data needs to be re-
structurized accordingly. The original algorithm uses
the RGBA-component texture format to communicate
between the kernels, hence the data is batched in a
four-component SIMD way. As four (independent)
disparity estimations are packed inside these compo-
nents, the data stream L0:3 – respresenting the four
components of the left convolution filter – and R0:3
are restructurized to L0:1R0:1 and L2:3R2:3, thus
crosswise switching the first and last two components
of the vectors. Since these components are indepen-
dent by definition of SIMD, the restructuring is al-
lowed because both vertical kernels exhibit the same
functionality. The four data streams that are required
by the WTA-kernel (i.e. UL, DL, UR, and DR), are
available at the output of a single vertical convolution
kernel, albeit only two components instead of four.
For this, the WTA-kernel has to be slightly modified
(devectorized), but in this case results in no penalty, as
the minimum selection is already a scalar operation.
In a final and fifth stage, the duplicated WTA-
kernels can be merged with the preceding vertical
convolutions, as depicted in Fig. 4e. The communi-
cation with global memory (i.e. legacy texture mem-
ory) can therefore be avoided. Since the dependencies
between the WTA- and convolution kernels exhibit a
one-to-one relationship (i.e. selecting the minimum),
the merge can be carried out implicitly.
To give an indication of the overall performance
gain, we have benchmarked the phase 3 (as origi-
nally proposed by Lu et al.) and phase 5 implemen-
tation, as suggested by the high-level kernel trans-
formation rules. The implementations where mea-
sured on an NVIDIA GeForce 8800GT, using im-
ages with a 450 × 375 resolution and 60 disparity es-
timations. The phase 3 implementation gives 115fps,
while phase 5 reaches over 129fps, resulting in an in-
crease of 12.2%. However, the overall performance
increase (phase 2 until 5) is over 40% with minimal
design effort.
4 CONCLUSIONS
We have proposed a high-level rule set to trans-
form the original algorithmic design, resulting in an
inter-kernel optimization rather then a low-level intra-
kernel optimization. Since the rules take both tra-
ditional texture caches and next-gen shared memory
into account, they can be implicitely applied in most
streaming applications on graphics hardware. We
have applied the rule set to a state-of-the-art depth
estimation algorithm, and achieved over 40% perfor-
mance increase with minimal design effort.
ACKNOWLEDGEMENTS
Sammy Rogmans would like to thank the IWT for the
financial support under grant number SB071150.
REFERENCES
Asanovic, K., Bodik, R., Catanzaro, B. C., Gebis, J. J.,
Husbands, P., Keutzer, K., Patterson, D. A., Plishker,
W. L., Shalf, J., Williams, S. W., and Yelick, K. A.
(2006). The landscape of parallel computing research:
A view from berkeley. Technical report.
Fatahalian, K., Sugerman, J., and Hanrahan, P. (2004).
Understanding the efficiency of GPU algorithms for
matrix-matrix multiplication. In Graphics Hardware.
Gong, M., Yang, R., Wang, L., and Gong, M. (2007). A
performance study on different cost aggregation ap-
proaches used in real-time stereo matching. Int’l Jour-
nal Computer Vision.
Govindaraju, N. K., Larsen, S., Gray, J., and Manocha, D.
(2006). A memory model for scientific algorithms on
graphics processors. In Super Computing.
Lu, J., Lafruit, G., and Catthoor, F. (2007). Fast vari-
able center-biased windowing for high-speed stereo
on programmable graphics hardware. In ICIP.
Owens, J., Luebke, D., Govindaraju, N., Harris, M., Kruger,
J., Lefohn, A., and Purcell, T. (2007). A survey of
general-purpose computation on graphics hardware.
CG Forum.
Podlozhnyuk, V. (2007). Image convolution with CUDA.
Rogmans, S., Lu, J., Bekaert, P., and Lafruit, G. (2009).
Real-time stereo-based view synthesis algorithms:
A unified framework and evaluation on commodity
gpus. Signal Processing: Image Communications.
Ryoo, S., Rodrigues, C. I., Baghsorkhi, S. S., Stone, S. S.,
Kirk, D. B., and Hwu, W.-M. W. (2008). Optimization
principles and application performance evaluation of a
multithreaded GPU using CUDA. In PPoPP.
Scharstein, D. and Szeliski, R. (2002). A taxonomy and
evaluation of dense two-frame stereo correspondence
algorithms. Int’l Journal Computer Vision.
A HIGH-LEVEL KERNEL TRANSFORMATION RULE SET FOR EFFICIENT CACHING ON GRAPHICS
HARDWARE - Increasing Streaming Execution Performance with Minimal Design Effort
43
