DOUBLE

WELL POTENTIAL AS DIFFUSIVE FUNCTION

FOR PDE-BASED SCALAR IMAGE RESTORATION METHOD

A. Histace

ETIS UMR CNRS 8051, ENSEA-UCP, 6 avenue du Ponceau, 95014 Cergy, France

M. M

enard

L3i, University of La Rochelle, Pole Sciences et Technologie, 17000 La Rochelle, France

Keywords:

Image Diffusion, Double well potential, Directional diffusion, Selectivity.

Abstract:

Anisotropic regularization PDE’s (Partial Differential Equation) raised a strong interest in the ﬁeld of image

processing. The beneﬁt of PDE-based regularization methods lies in the ability to smooth data in a nonlinear

way, allowing the preservation of important image features (contours, corners or other discontinuities). In this

article, we propose a PDE-based method restoration approach integrating a double-well potential as diffusive

function. It is shown that this particular potential leads to a particular regularization PDE which makes it

possible integration of prior knowledge about the gradients intensity level to restore. As a proof a feasibility,

results of restoration are presented both on ad hoc and natural images to show potentialities of the proposed

method.

1 INTRODUCTION

Since the pioneering work of Perona-Malik (Perona

and Malik, 1990), anisotropic regularization PDE’s

raised a strong interest in the ﬁeld of image process-

ing. Many regularization schemes have been pre-

sented so far in the literature, particularly for the

problem of scalar image restoration (see (Histace and

enard, 2008) for a complete review). In (Deriche

and Faugeras, 1996) authors propose a synthetic for-

mulation to express the global scheme of PDE-based

restoration approaches. More precisely, if we denote

ψ(r,t) : R

×R

→ R the time intensity function of a

corrupted image ψ

= ψ(r,0), the corresponding reg-

ularization problem of ψ

is equivalent to the mini-

mization problem described by the following PDE:

∂ψ

∂t

= c

(k∇ψk)

∂

∂ξ

+ c

(k∇ψk)

∂

∂η

, (1)

where η = ∇ψ/k∇ψk, ξ⊥η and c

and c

are

o weighting functions (also called diffusive func-

tions). This PDE can be interpreted as the super-

position of two monodimensional heat equations, re-

spectively oriented in the orthogonal direction of the

gradient and in the tangential direction: It is charac-

terized by an anisotropic diffusive effect in the priv-

ileged directions ξ and η allowing a non-linear de-

noising of scalar image. Eq. (1) is of primary im-

portance, for all classical methods can be expressed

in that global scheme: For instance, if we consider

the former anisotropic diffusive equation of Perona-

Malik’s (Perona and Malik, 1990) given by

∂ψ

∂t

= d

iv(c(k∇ψk)∇ψ) , (2)

with ψ(r,0) = ψ

and c(.) a monotonic decreasing

function, it is possible to express it in the global

scheme of Eq. (1) with

(

= c(k∇ψk)

= c

(k∇ψk).|∇ψ| + c(k∇ψk)

(3)

Formulation of Eq. (1) is also interested, for it makes

stability study of classical proposed methods possi-

ble. What we proposed in this article is a prospective

study for the integration of a double well potential

as a diffusive function c(.) in Eq. (2). Our aim and

motivation for such a study are mainly to show that,

ﬁrstly, such a choice can lead to a stable PDE-based

approach for scalar image denoising that can over-

pass classical approach of Perona-Malik’s from which

it is derived and which presents instability problems

as formerly shown in (Catt

e et al., 1992), and, sec-

ondly, that this approach overcomes some drawbacks

of the classical methods like corner smoothing or pin-

hole effect. Layout of this article is the following one:

401

Histace A. and Ménard M. (2009).

DOUBLE WELL POTENTIAL AS DIFFUSIVE FUNCTION FOR PDE-BASED SCALAR IMAGE RESTORATION METHOD.

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 401-404

DOI: 10.5220/0002191304010404

 SciTePress

In section two, we introduce the double well func-

tion and derive the corresponding PDE in the global

scheme of Eq. (1). We also proposed in that section a

study of the stability of the derived PDE compared to

the stability of Perona-Malik’s approach. Third sec-

tion is dedicated to experimental and quantitative re-

sults. Fourth and last section contains conclusion and

discussion.

2 DOUBLE WELL POTENTIAL

AND CORRESPONDING PDE

2.1 Diffusive Function

The double well potential considered in this article is

deﬁned by the following function:

(u) = 1 −φ(u) = 1 −

v(α− v)(v − 1)dv . (4)

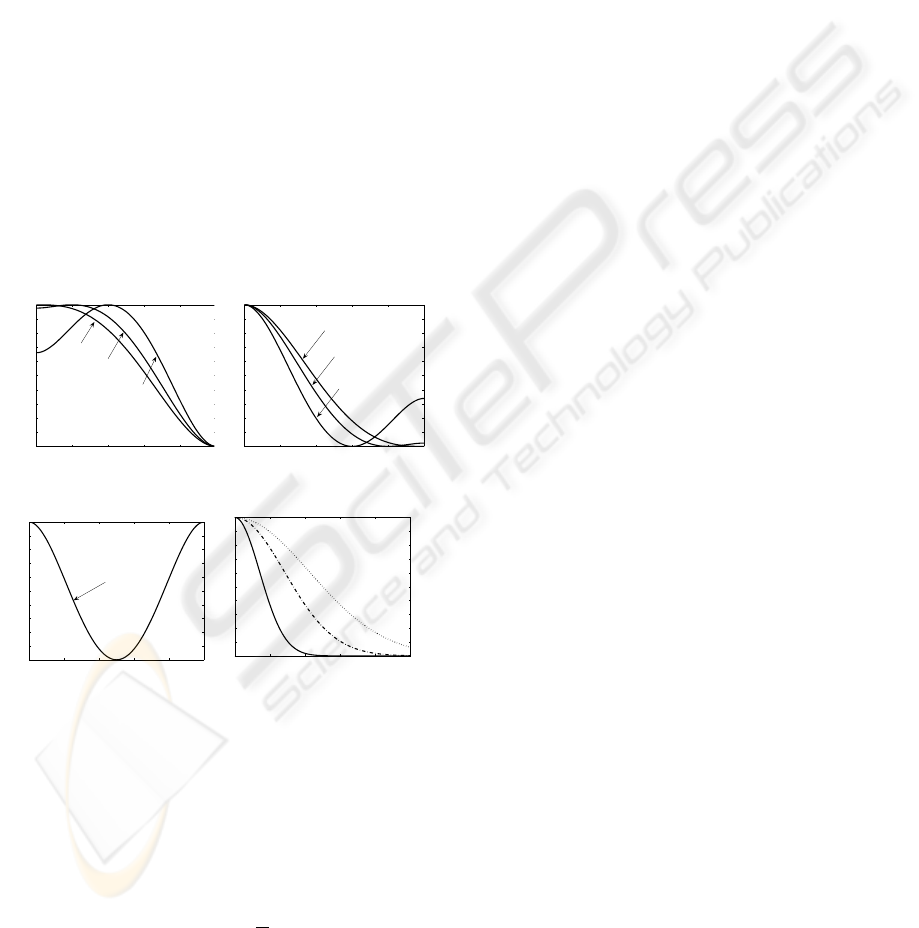
Some graphical representations of Eq. (4) for differ-

ent values of α are proposed Fig. 1.

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(u)

α=0

α=0.2

α=0.4

(a)

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(u)

α=1

α=0.8

α=0.6

(b)

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(u)

α=0.5

(c)

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(u)

(d)

Figure 1: (a), (b), (c) Plots of function c

(.) of Eq. (4)

for different values of α: (a) 0 < α < 0.5, (b) 0.5 < α < 1,

and (c) α = 0.5. (d) Plots of function c

(.) of Eq. (5) for

different values of k and α. Solid lines stand for k = 0.2,

dash-dotted lines for k = 0.4, and dotted lines for k = 0.6.

This function has to be compared with the classical

Perona-Malik’s function c

(.) given by:

(u) = e

−

, (5)

with k a soft threshold deﬁning selectivity of

(.) regarding values of image gradients. Fig. 1.(d)

shows graphical representations of c

(.) deﬁned by

Eq. (5) for different values of k. As one can notice on

Fig. 1.(d), for k∇ψk → 0, c

(k∇ψk) → 1, whereas

for k∇ψk → 1, c

(k∇ψk) → 0. As a consequence,

boundaries within images which are on a threshold,

function of k, are preserved from the smoothing ef-

fect of Eq. (2). One can notice on Fig. 1 that φ(.)

has been normalized. As a consequence, we are able

to ensure that 0 ≤ c

(u) ≤ 1 for all values of u like

classical PM’s function of Eq. (2). Global variations

of c

can be compared to those of c

for α = 0

and α = 1. For 0 ≤ α < 1, since c

is issued from

a double well potential, selectivity of Eq. (2) is more

important and centered on a particular gradient value

function of α. For instance, for α = 0.5, only gradi-

ents of value 0.5 are totally preserved from the diffu-

sive effect that can be interpreted as an integration of

directional constrains within the restoration process.

Moreover, we are now going to show, that integration

of c

as diffusive function leads to interesting sta-

bility property of corresponding PDE.

2.2 Study of Stability

As mentioned in ﬁrst section, classical Perona-

Malik’s PDE presents instability problems. More pre-

cisely, as shown in (Catt

e et al., 1992), sometimes

noise can be enhanced instead of being removed. This

can be explained considering Eq. (3). If we con-

sider c

(.) function, it appears that corresponding c

function of Eq. (3), in the global scheme of Eq. (1),

can sometimes takes negative values (see Fig. 2.(a)

for illustrations). This leads to local instabilities of the

Perona-Malik’s PDE which degrades the processed

image instead of denoising it. Now, if we calculate

mathematical expression of c

with c(.) = c

(.) of

Eq. (4), one can obtain that:

(k∇ψk) = c

(k∇ψk).|∇ψ| + c

(k∇ψk) , (6)

Considering Eq.(6), if we plot this function, one can

notice that corresponding c

function never takes neg-

ative values (see Fig. 2.(b) for illustrations): Diffusive

process remains stable for all gradient values of pro-

cessed image which is of primary importance.

3 EXPERIMENTAL RESULTS

We propose in this section to make a visual and quan-

titative comparison between classical Perona-Malik’s

PDE of Eq. (2) with diffusive function c(.) = c

(.)

of Eq. (5), and proposed derived PDE with c(.) =

(.) of Eq. (4) as diffusive function. For quantita-

tive comparisons, we will consider adapted measure

of similarity between non corrupted initial image and

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

402

0 0.2 0.4 0.6 0.8 1

−0.5

0.5

(a)

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

(b)

Figure 2: Plots of function c

and c

for different val-

ues of k and α. Solid lines stand for k = 0.2 and α = 0.5,

dash-dotted lines for k = 0.4 and α = 0.7 and dotted lines

for k = 0.6 and α = 1.

restored one. This measure will depend on the nature

of original image. For practical numerical implemen-

tations, the process of Eq. (2) is sampled with a time

step τ. The restored images ψ(t

) are calculated at

discrete instant t

= nτ with n the number of itera-

tions.

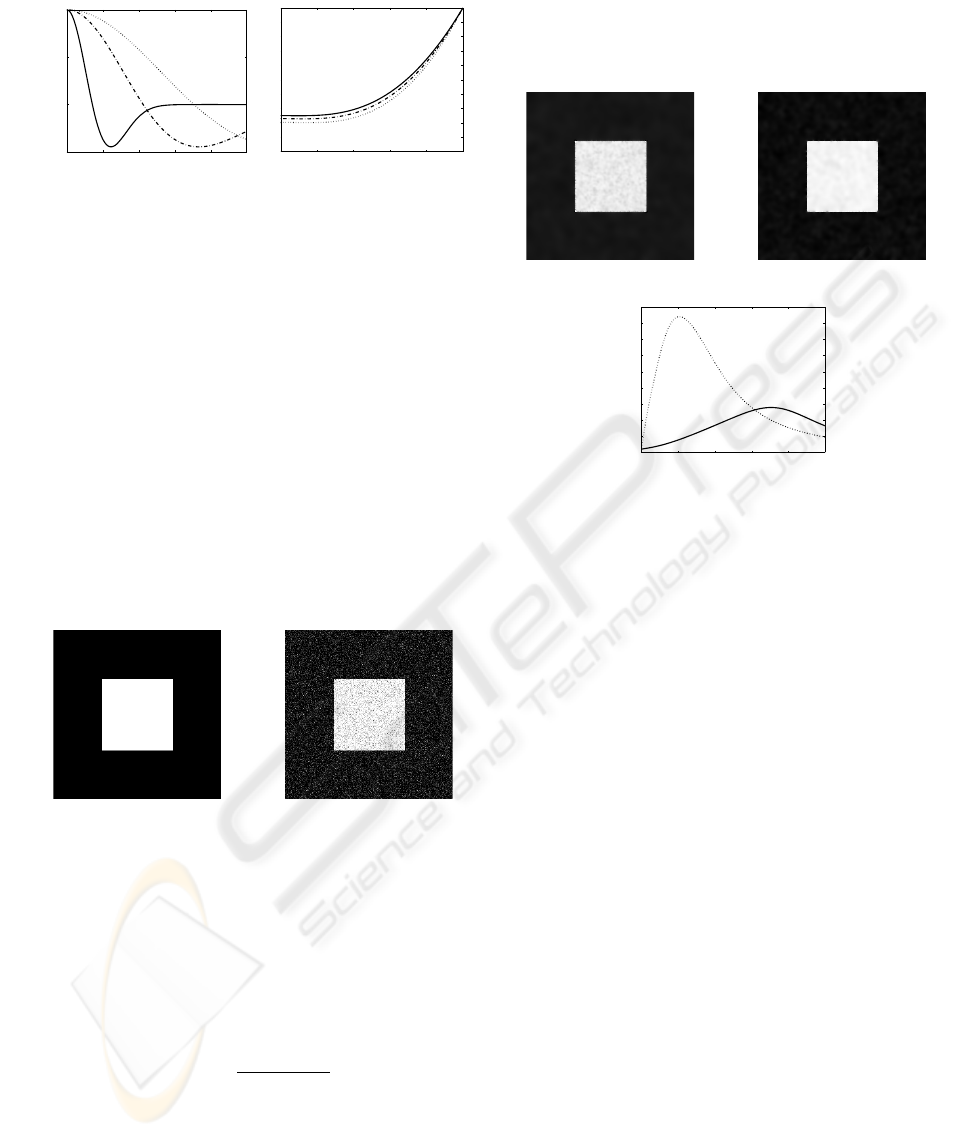
3.1 Synthetic Image

The ﬁrst proposed image is the binary image of Fig.

3.(a) corrupted by a white gaussian noise of mean zero

and standard deviation σ.

(b)

(w)

(a) (b)

Figure 3: (a) Original synthetic image and (b) its corrupted

version ψ

. Corrupting noise is a white Gaussian one of

mean zero and standard deviation σ = 0.05.

Considering binary nature of non corrupted image

(Fig. 3.(a)), quantiﬁcation of the denoising effect of

Eq. (2) with c(.) = c

(.) and c(.) = c

(.), will be

estimated with Fisher’s index given by

Fisher

− m

)

+ σ

, (7)

with m

w,b

the average value of the pixels of the re-

stored image ψ(t

) being originally in the white (w)

or black (b) part of original image (Fig. 3.(a)) and

w,b

the corresponding standard deviation. Because

aim of this article is to show potentiality of the de-

scribed restoration method, only optimal results for

both compared approaches are presented Fig. 4: Val-

ues of k and α parameters are empirically chosen and

strategy for optimal choice is not describe here.

(a) (b)

0 100 200 300 400 500

100

200

300

400

500

600

700

800

900

Fisher

(c)

Figure 4: (a) Restored image with c(.) = c

(.) (classical

Perona-Malik’s approach), (b) Restored image with c(.) =

(.) (proposed approach), (c) Fisher index function of

iteration number n, solid lines stands for classical Perona-

Malik’s approach, dotted line stands for proposed method.

k is equal to 0.4, α is equal to 0.5 (these values have been

empirically tuned).

As one can notice on Fig. 4, both visually and

quantitatively, restoration of binary image of Fig.

3.(a) is better with the diffusive function of Eq. (4).

More precisely, stability property of the double well

function prevents restoration process from possible

enhancement of corrupting Gaussian noise. Homoge-

nous areas of Fig. 4.(b) does not visually shows os-

cillations, nor corners of the white square as in Fig.

4.(a). This visual impression is conﬁrmed by vari-

ations of Fisher’s index in Fig. 4.(c) that reaches a

level third times more important than with classical

approach of Perona-Malik’s. The value of α parame-

ter corresponding to best result is 0.5: this is not sur-

prising, for it is also the value of the gradient intensity

characterizing the boundaries of the with square. As a

consequence, this experiment also conﬁrmed the pos-

sible gradient intensity selectivity of the proposed ap-

proach interpreted as a directional diffusion process.

We shall now experiment the proposed approach in

the context of restoration of real scalar images.

3.2 Real Images

In this section, we propose to compare both our pro-

posed method with PM’s approach on the classical

DOUBLE WELL POTENTIAL AS DIFFUSIVE FUNCTION FOR PDE-BASED SCALAR IMAGE RESTORATION

METHOD

403

“cameraman” image. For our purpose, this latter has

been corrupted by a white gaussian noise of mean

zero and standard deviation σ (see Fig. 5).

(a) (b)

Figure 5: (a) Original image “cameraman” and (b) its cor-

rupted version ψ

. Corrupting noise is a white Gaussian one

of mean zero and standard deviation σ = 0.05.

Considering nature of non corrupted image (Fig.

5.(a)), quantiﬁcation of the denoising effect of Eq.

(2) with c(.) = c

(.) and c(.) = c

(.), will be es-

timated with a classical PSNR measurement. Once

again, because aim of this article is to show potential-

ity of the described restoration method, only optimal

results for both compared approaches are presented

Figs. 6 and 7.

(a) (b)

Figure 6: (a) Restored image with c(.) = c

(.) (clas-

sical Perona-Malik’s approach), (b) Restored image with

c(.) = c

(.) (proposed approach). k is equal to 1 for

PM’s restoration approach, α is equal to 0.2 for proposed

approach (these values have been empirically tuned).

One can notice on Figs. 6 and 7 that both visu-

ally and quantitatively, it is possible to ﬁnd a value

of α that can outperform results of classical PM’s ap-

proach. Quantitatively speaking PSNR is around 2dB

higher and visually speaking, boundaries on Fig. 6 are

preserved in a better way from the diffusion effect.

4 CONCLUSIONS

In this article, we have proposed an alternative diffu-

sive function for restoration of scalar images within

the framework of PDE-based restoration approaches.

The proposed diffusive function allows integrating

0 20 40 60 80 100 120

132

134

136

138

140

142

144

146

148

iteration number (n)

PSNR (dB)

Figure 7: PSNR function of iteration number n, solid lines

stands for classical Perona-Malik’s approach, dotted line

stands for proposed method. k is equal to 1, α is equal to

0.2 (these values have been empirically tuned). These two

curves have been computed by calculation of the mean re-

sults obtained for one hundred different realizations of the

gaussian corrupting noise.

prior knowledge on the gradient level to restore thanks

parameter α of Eq. (4) and remains always stable

on the contrary of classical PM’s approach. Pro-

posed method also remains fast and easy to com-

pute. Quantitatively speaking, better restoration re-

sults have been obtained. Concerning possible out-

looks, this proposed method could be associated to

the orientation selectivity of a PDE-based method al-

ready presented in the framework of that conference

in (Histace et al., 2007). Association of both proper-

ties should lead to a restoration method with interest-

ing directional properties for “vision in robotics” area

for example.

REFERENCES

Catt

e, F., Coll, T., Lions, P., and Morel, J. (1992). Im-

age selective smoothing and edge detection by nonlin-

ear diffusion. SIAM Journal of Applied Mathematics,

29(1):182–193.

Deriche, R. and Faugeras, O. (1996). Les edp en traitements

des images et visions par ordinateur. Traitement du

Signal, 13(6):551–578.

Histace, A., Courboulay, V., and M

enard, M. (2007). Selec-

tive image diffusion for oriented pattern extraction. In

4th International Conference on Informatics in Con-

trol, Automation and Robotics (ICINCO), pages 270–

274.

Histace, A. and M

enard, M. (2008). Robotics, Automation

and Contol Book: PDE based approach for oriented

pattern segmentation, chapter 22, pages 207–218. In-

tech Education and Publishing.

Perona, P. and Malik, J. (1990). Scale-space and edge

detection using anistropic diffusion. IEEE Transca-

tions on Pattern Analysis and Machine Intelligence,

12(7):629–639.

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

404