LINEAR IDENTIFICATION OF

ROTARY WHITE CEMENT KILN

Golamreza Noshirvani, Mansour Shirvani

ACECR Markazi Branch, Beheshti Street, Arak, Iran

Alireza Fatehi

Control Departmen , KNtoosi University, Tehran, Iran

Keywords: Rotary White Cement Kiln, Dynamic Modelling, Linear Identification, Box-Jenkins.

Abstract: Rotary cement kiln is the main part of a cement plant that clinker is produced in it. Continual and prolonged

operation of rotary cement kiln is vital in cement factories. However, continual operation of the kiln is not

possible and periodic repairs of the refractory lining would become necessary, due to non-linear phenomena

existing in the kiln, such as sudden falls of coatings in the burning zone and probability of damages to the

refractory materials during production. This is the basic reasoning behind the needs for a comprehensive

model which is severely necessary for better control of this process. Such a model can be derived based on

the mathematical analysis with consultation of expert operator experiences. In this paper linear model is

identified for rotary kiln of Saveh white cement factory. The linear model is introduced using Box-Jenkins

structure. The results of the obtained model were satisfactory compared to some other models and can be

used for designing adaptive or robust controllers.

1 INTRODUCTION

During the years of clinker production, many

changes and improvements have been occurred.

Rotary kilns is not just for cement production, while

it is used in different chemical industries such as

lime burning, crude oil calcinations, solid garbage

ash, titanium dioxide calcinations, aluminium oxide

process and etc. In all cases, use of rotary kiln, due

to its basic role about energy consumption, desired

reaction performance and many other advantages is

preferred. However, control of the kiln in optimal

condition is of primary importance and is not

possible unless having a good knowledge and a

comprehensive model based on important

phenomena occurring in the system. In this way,

several research papers have been published among

which the original modelling of Spang, based on

material and energy balance of the kiln can be

mentioned (Spang, 1972). In Spang’s

mechanistically model several assumptions have

been used. Also, Frish assumed the kiln as

cylindrical vessel with internal non adiabatic heating

source, and focused on the monotonically state. He

assumed the heat transfer based on radiated rather

than displacement type (Frish and Jeschar, 1983). In

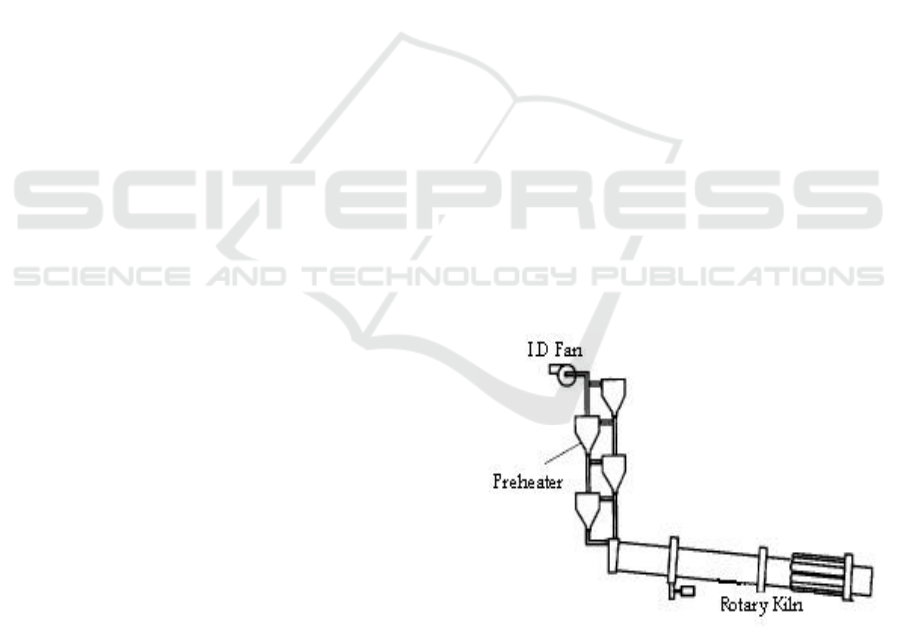
figure 1, a schematic of the kiln with its cyclone pre-

heater is shown.

Figure 1: Rotary Cement kiln Process.

In this paper we will use a black box

identification procedure for modelling the Saveh

white cement kiln. It is a 65 m long, 4.7 m diameter

kiln with 4 stage double string pre-heater and water

immersion cooler. The main manipulated variables

of the kiln are:

190

Noshirvani G., Shirvani M. and Fatehi A.

LINEAR IDENTIFICATION OF ROTARY WHITE CEMENT KILN.

DOI: 10.5220/0002191501900195

In Proceedings of the 6th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2009), page

ISBN: 978-989-674-001-6

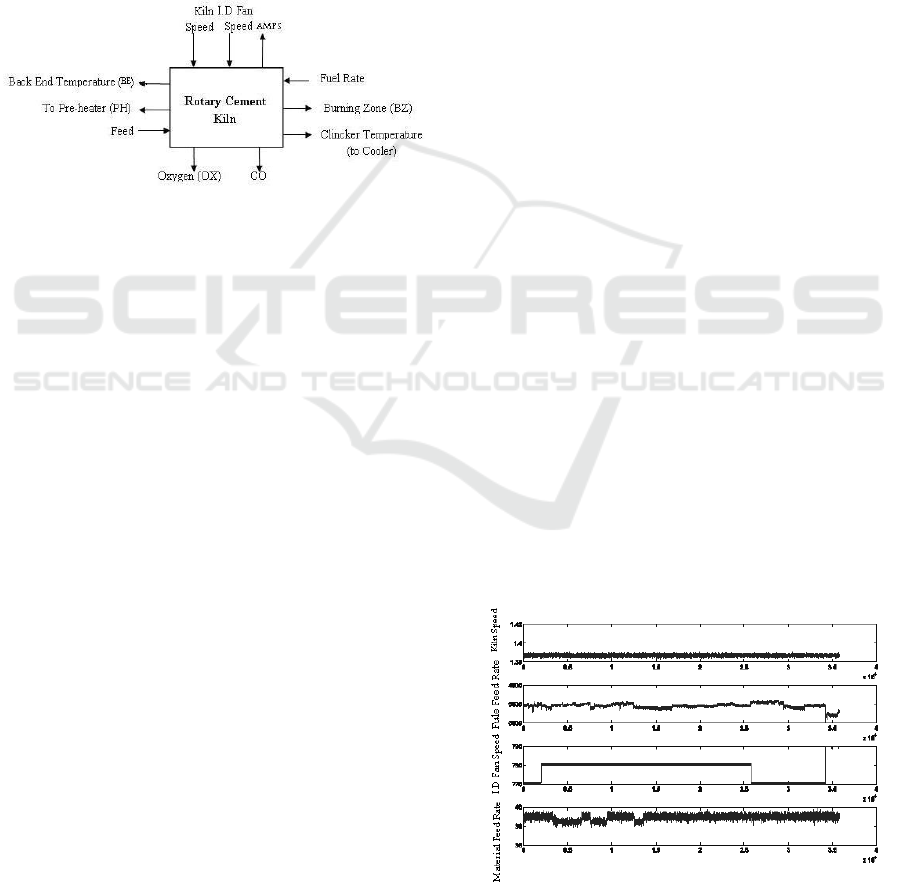
 kiln speed

 Fuel Flow Rate

 ID. Fan speed

 Raw Material Flow Rate

Also the output variables according to the

operator’s experiences are as following:

 back end temperature

 Remained (unused) oxygen, O

 CO content of outlet gases from the kiln

 Kiln DC motor current

 Preheater temperature

 Cooler temperature

Based on these variables the rotary kiln is a 4-

inputs 6-outputs plant as shown in figure 2.

Figure 2: Block diagram of the kiln based on input-output.

These variables are so important and selected

with fundament of expert operators, such as with

these input, the kiln can be controlled. The burning

zone temperature is not only one of the most

important kiln control variables but also the most

difficult one to monitor (Peray, 1986). Despite the

fact that burning zone condition in modern kilns are

shown as temperature profile that used for manual

controllers.

2 CONDITION OF DATA

GATHERING

There are three important factors in modelling based

on the identification techniques:

 Useful and valid data

 A perfect and useful model

 Strong method to adjust the model

Input and outputs must be selected such that

input change affects output variables. Also the

recognition of process behavior will be much

simpler if input-output data is reach, i.e. it consists

different operating points and frequency contents.

However, system identification based on input

output data does not introduce a physical model with

exact structure but it does a model that fits the data.

Therefore, selection of a proper model is important.

Also, the obtained data should have the process

information to be used for identification.

An important point concerning data gathering is

that to be careful that the disturbances and

unexpected events such as creation of coating and

coating fall in the kiln and do not change the system

behaviour. The white cement rotary kiln

identification is passive process, meaning that we

can only observe the plant variables under a given

circumstance and it is technically impossible to

introduce extra excitation on these systems. The data

from these systems may not be informative enough.

This can make the identification of the system

difficult (Zhu, 2001). Therefore it is not possible to

expect from the presented model to have the same

behaviour with the real system in an abnormal

condition unless these conditions are occurred a few

times during data gathering.

For this reason, data gathered during a period of

18 hours for several times. Finally, the best

conditioned data were obtained for the rotary kiln in

2008-05-07. Figure 3 shows the input variables. The

output variables are shown in figure 4.

3 DATA PRETREATMENT

After collecting perfect data from rotary kiln, the

data will not be used directly for identification

process. One of its reasons is high frequency noises

and spikes on the main signals. Sometimes

immeasurable disturbances occur and take the

system out of its linear range. Changing Operation

point causes entering nonlinear effects in output

data. To solve the problem of high frequency noises

and some of these problems, it is tried to use some

pre-processing methods mentioned in identification

references to reach a perfect model of process

(Ljung, 1999; Nelles, 2001) . For considering rest of

them, we tried to choose the model structure and

focus on its flexibilities.

Figure 3: Input data representation for white cement kiln

identification.

LINEAR IDENTIFICATION OF ROTARY WHITE CEMENT KILN

191

Figure 4: Output data representation for white cement kiln

identification.

3.1 Peak Shaving

At the first stage, it is necessary to pay attention on

data to recognize the system dynamics based on the

available input and output data. It is important to

smooth the spikes and shave the peaks. Spikes are

because of sensors operation or data acquisition card

that causes a numerical fault in data representation

(Astrom, 1984), whereas the high energy of spikes

interfere the model parameters estimation and its

validation. Applying a third order digital

Butterworth filter on the data gathered from the kiln.

The filtered output for kiln back temperature is

shown in figure 5. Correlation analysis is used to

obtain the weight and important dynamics between

input and output data (Noshirvani, 2005). The

similarity of two signals will be measured in

correlation analysis. In this analysis, the correlation

order of two signals is measurable. These contexts

can be written as the following formulas:

kyku

tytuE

)()(

lim)()()(

(1)

where

u,y

( ) is the cross correlation of u and y and

kuku

tutuE

)()(

lim)()()(

(2)

where

u,u

( ) is the autocorrelation of u.

Correlation analysis assumes a linear system and

does not require a specific model structure; also it

could be used to assess the effective dynamics.

Figure 6 shows the correlation between input

fuel rate and the kiln speed to burning zone

temperature.

Figure 5: Real data and Filtered data representation.

The basic assumption in the discussion is that the

identification model will be used in control.

Therefore the main dynamics used for this output in

identification have been shown, and then the plant is

broken into 6 MISO models.

Figure 6: Correlation between first and second inputs with

the first output.

4 LINEAR IDENTIFICATION

Different linear models were studied for system

identification. The best obtained linear model for the

kiln was Box-Jenkins (BJ) model which its result is

explained here. BJ model is defined as:

( ) ( )

( ) ( ) ( )

( ) ( )

B q C q

y k u k k

F q D q

(3)

This structure has been introduced by Box-

Jenkins in 1970. The predictor for this model is

illustrated in (5).

Important Dynamics

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

192

()

()yk

()uk

( )k

Figure 7: Box-Jenkins Structure.

qdqdqD

qcqcqC

qbqbqB

qfqfqF



1)(

)(

1)(

(4)

( ) ( ) ( )

( 1) ( ) 1 ( )

( ) ( ) ( )

D q B q D q

y k k u k y k

C q F q C q

(5)

where

)(

is the output of the model. The notation

|k-1 is used because the optimal prediction of Box-

Jenkins model utilizes previous process outputs in

order to extract the information contained in the

correlated disturbance, n(k) affects on output

variable, that is defined in (6) and the prediction of

error of this model can be obtained with (7).

( ) ( ) ( )

D q B q D q

e k y k u k

C q F q C q

(6)

Box-Jenkins model is estimated by nonlinear

optimization, where first an auto regressive

estimation to determine the initial parameter values

for b

and f

. The gradients of models function can be

computed as follows.

( ) ( ) ( 1) ( ) ( ) ( )

( ) ( ) ( ) ( )

F q C q y k k B q D q u k

F q C q D q y k

(7)

Differentiation of (7) with respect to b

yields

( 1)

( ) ( ) ( ) ( )

y k k

F q C q D q u k i

(8)

This leads to

( 1)

()

( ) ( )

y k k

u k i

b F q C q

(9)

Also these computations have done for c

, d

and

. The parameters of this model will be trained based

on minimizing of the following cost function:

)(

(10)

The main advantage of Box-Jenkins is giving a

better estimation for the closed-loop models, but its

implementation is a challenging task (Eykoff, 1974).

In general Box-Jenkins (BJ) model has several

advantages over the output error method. Firstly, it

will supply both a process model and a disturbance

model. As shown in table1, this model will be

consistent also in passive identification; this implies

that this method will give a more accurate process

model than an output error method for a given

process under passive data condition. However, the

BJ model has a more complex structure, which

implies that numerical optimization will be more

complicated.

Figure 8: Actual and simulated signal of

kiln back-end temperature.

Figure 9: Actual and simulated signal

of Kiln motor current.

Carbon monoxide analysis, because it samples

dirty kiln gases and takes the sample at a location

where high temperature prevail, has a tendency to

multifunction frequently unless almost daily

preventive maintenance is carried out on this unit.

The location, where the sample probe is installed, is

LINEAR IDENTIFICATION OF ROTARY WHITE CEMENT KILN

193

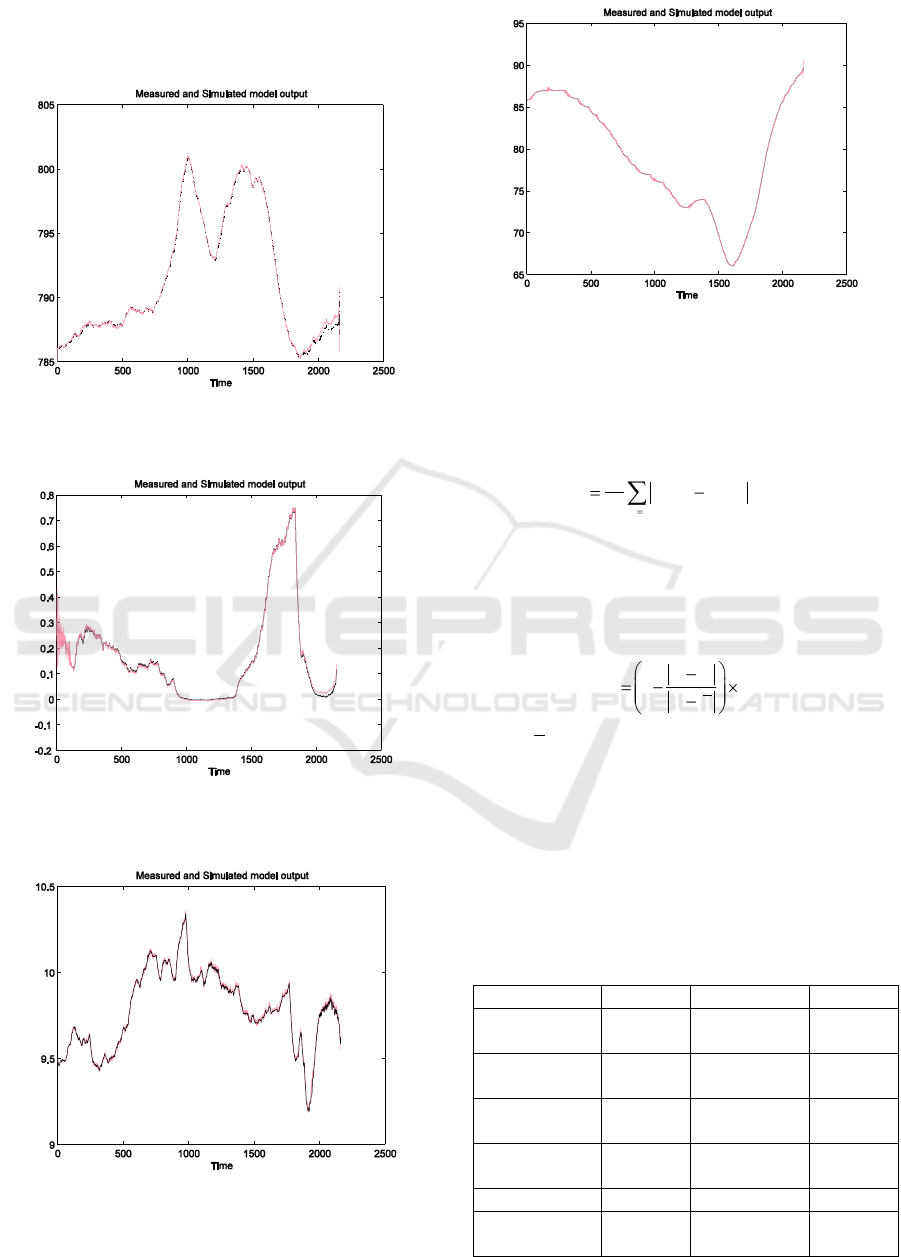
also key point to consider as false air in leakage

could distort the true contents of CO in the exit

gases (Shirvani et.al, 2004).

Figure 10: Actual and simulated signal of Pre-heater

temperature.

Figure 11: Actual and simulated signal of

Carbon monoxide.

Figure 12: Actual and simulated signal of Oxygen.

Figure 13: Actual and simulated signal of

Cooler temperature.

Equation11 is known as the mean square error of

model. It is an estimation of the standard deviation

of the model error with respect to data.

( ) ( )

E y k y k

(11)

The models are compared with test data that

obtained also in 2008-08-15 for # hours from control

system of Saveh white cement plant. The fitness of

the model with the plant can be computed as

(Eykoff, 1974). Then the best criterion is (12).

1 100

fitness

(12)

where

()yk

is the mean of y(k).

By comparing different dynamic models like

output error (OE) and ARMAX in equation (12) can

be concluded that BJ modelling has a better response

(Noshirvani, 2005). This result is because passive

modelling of kiln system is severely non-linear.

Therefore, as it is shown in Table1, the most

enriched linear model has relatively better

performance.

Table 1: comparing different linear Models of plant.

Variable

B.J.

ARMAX

O.E.

Back end

temperature

85%

64%

37%

Current

motor Kiln

84%

70%

29%

Preheater

Temperature

91%

75%

40%

Carbon

mono oxide

88%

68%

39%

Oxygen

89%

68%

30%

Cooler

temperature

87%

61%

35%

ICINCO 2009 - 6th International Conference on Informatics in Control, Automation and Robotics

194

5 CONCLUSIONS

In this paper, some linear approaches for system

identification and model parameter estimation have

been applied to an industrial scale white cement kiln.

Since the white cement rotary kiln identification

is passive and the process input data were

inadequate and the signal to noise rate was very

high, it is a complex process which needs some

comprehensive identification procedure. Different

kind of linear models are examined in which BJ

dynamic model presents the best result compare to

other linear models.

Linear structure can be used for identifying the

rotary cement kilns, but in this procedure, the

coating fall and its creation in the kiln, will be

ignored. Thus, the train and test data have been

gathered with this assumption.

Weakness of linear modelling based on O.E is

that it is proper for slow damping process, but in this

plant slow dynamics related to the system and fast

dynamics related to noise are not completely

segregated and obtained error is mostly related to

enforced noise in output signals.

REFERENCES

Spang, H.A., 1972. Dynamic Model of a Cement kiln,

Vol. 8, pp. 309 – 323,

Frish, V., Jeschar, R., 1983. Possibilities for Optimizing

the Burning Process in Rotary Kiln,

Vol. 10/83, pp.549-560,

Peray, K.E., 1986. The Rotary Cement Kiln, 2

edition

Zhu, Y.C., 2001. Multivariable System Identification for

process control, PERGAMON

Ljung, L., System Identification: Theory for the user. 1999

Prentice- Hall, 2

edition

Nelles, O., 2001. Nonlinear system identification, Springer

Astrom, K. J. and Wittenmark, B., 1984. Computer

Controlled Systems: Theory and Design, Prentice-

Hall, Englewood Cliffs

Noshirvani, R., Identification of White Cement Rotary

Cement Kiln, M.Sc Thesis, K.N.Toosi University

Control Engineering Department of K.Ntoosi, 2005

Eykoff, P., 1974. System Identification: Parameter and

state Estimation, John Wiley & Sons, New York

Shirvani, M., Dustary, M., Shahbaz, M. Eksiri, Z.

Heuristic, 2004. Process Model Simplification

inFrequency Response Domain, International of

Engineering, Vol. 17/B, pp.31-52

LINEAR IDENTIFICATION OF ROTARY WHITE CEMENT KILN

195